HBSE 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.4

[नोट- जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
निम्न त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 10.5 सें०मी०
(ii) 5.6 सें०मी०
(iii) 14 सें०मी०
हल :
(i) यहां पर,
गोले की त्रिज्या (r) = 10.5 सें०मी० = \(\frac{105}{10}\) सें०मी० = \(\frac{21}{2}\) सें०मी०
∴ गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\) सें०मी०
= 1386 सें०मी०² उत्तर

(ii) यहां पर,
गोले की त्रिज्या (r) = 5.6 सें०मी० = \(\frac{56}{10}\) सें०मी०
∴ गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac{22}{7} \times \frac{56}{10} \times \frac{56}{10}\) सेमी
= \(\frac{39424}{100}\) में.मी०²
= 394.24 सें०मी० उत्तर

(iii) यहां पर,
गोले की त्रिज्या (r) = 14 सें०मी०
∴ गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac{22}{7}\) × 14 × 14 सें०मी०²
= 2464 सें०मी०² उत्तर

प्रश्न 2.
निम्न व्यास वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 14 सें०मी०
(ii) 21 से०मी०
(iii) 3.5 मी०
हल :
(i) यहां पर,
गोले का व्यास (d) = 14 सें०मी०
गोले की त्रिज्या (r) = \(\frac{14}{2}\) सें०मी० = 7 सें०मी०
∴ गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac{22}{7}\) × 7 × 7 सें०मी०
= 616 सें०मी०² उत्तर

(ii) यहां पर,
गोले का व्यास (d) = 21 सें०मी०
गोले की त्रिज्या (r) = \(\frac{21}{2}\) सें०मी०
∴ गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\) सें०मी०²
= 1386 सें०मी०² उत्तर

(iii) यहां पर,
गोले का व्यास (d) = 3.5 मी० = \(\frac{35}{10}\) मी० = \(\frac{7}{2}\) मी०
गोले की त्रिज्या (r) = \(\frac{7}{2 \times 2}\) मी० = \(\frac{7}{4}\) मी०
∴ गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac{22}{7} \times \frac{7}{4} \times \frac{7}{4}\) मी०²
= \(\frac{77}{2}\) मी०²
= 38.5 मी०² उत्तर

प्रश्न 3.
10 सें०मी० त्रिज्या वाले एक अर्धगोले का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल :
यहां पर,
अर्धगोले की त्रिज्या (r) = 10 सें०मी०
∴ अर्धगोले का कुल पृष्ठीय क्षेत्रफल = 3πr²
= 3 × 3.14 × 10 × 10 सें०मी०²
= 942 सें०मी०² उत्तर

प्रश्न 4.
एक गोलाकार गुब्बारे में हवा भरने पर, उसकी त्रिज्या 7 सें०मी० से 14 सें०मी० हो जाती है। इन दोनों स्थितियों में, गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
यहां पर,
पहली अवस्था में गुब्बारे की त्रिज्या (r₁) = 7 सें०मी०
पहली अवस्था में गुब्बारे का पृष्ठीय क्षेत्रफल = 4πr₁²
= 4 × \(\frac{22}{7}\) × 7 × 7 सें०मी०²
= 616 सें०मी०2
दूसरी अवस्था में गुब्बारे की त्रिज्या (r₂) = 14 सें०मी०
दूसरी अवस्था में गुब्बारे का पृष्ठीय क्षेत्रफल = 4πr₂²
=4 × \(\frac{22}{7}\) × 14 × 14 सें०मी०²
= 2464 सें०मी०²
दोनों अवस्थाओं में पृष्ठीय क्षेत्रफलों का अनुपात = क्षेत्रफल I : क्षेत्रफल II
= 616 : 2464
= 1 : 4 उत्तर

प्रश्न 5.
पीतल से बने एक अर्धगोलाकार कटोरे का आंतरिक व्यास 10.5 सें०मी० है। ₹ 16 प्रति 100 सें०मी० की दर से इसके आंतरिक पृष्ठ पर कलई कराने का व्यय ज्ञात कीजिए।
हल :
यहां पर,
अर्धगोलाकार कटोरे का अंतः व्यास (d) = 10.5 सें०मी० = \(\frac{105}{10}\) सें०मी० = \(\frac{21}{2}\) सें०मी०
अर्धगोलाकार कटोरे की अंतः त्रिज्या (r) = \(\frac{21}{2 \times 2}\)सें०मी० = \(\frac{21}{4}\) सें०मी०
∴ अर्धगोलाकार कटोरे का अंतः वक्र पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\frac{22}{7} \times \frac{21}{4} \times \frac{21}{4}\) × सें०मी०² = \(\frac{693}{4}\) सें०मी०²
100 सें०मी०² क्षेत्र पर कलई कराने का व्यय = ₹ 16
1 सें०मी०² क्षेत्र पर कलई कराने का व्यय = ₹ \(\frac{16}{10}\)
\(\frac{693}{4}\) सें०मी०² क्षेत्र पर कलई कराने का व्यय = \(\frac{693 \times 16}{4 \times 100}\) = ₹ \(\frac{2772}{100}\)
= ₹ 27.72 उत्तर

प्रश्न 6.
उस गोले की त्रिज्या ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 सें०मी० है। [B.S.E.H. March, 2020]
इल:
माना गोले की त्रिज्या = r सें०मी०
∴ गोले का पृष्ठीय क्षेत्रफल = 154 सें०मी०²
⇒ 4πr² = 154
या 4 × \(\frac{22}{7}\)r² = 154
या \(\frac{88}{7}\)r2 = 154
या r² = \(\frac{154 \times 7}{88}=\frac{49}{4}\)
या r = \(\sqrt{\frac{49}{4}}\)
या r = \(\frac{7}{2}\) सें०मी० = 3.5 सें०मी०
अतः गोले की त्रिज्या = 3.5 सें०मी० उत्तर

प्रश्न 7.
चंद्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। इन दोनों के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
माना पृथ्वी का व्यास = 2x मी०
पृथ्वी की त्रिज्या = \(\frac{2 x}{2}\) = x मी०
पृथ्वी का पृष्ठीय क्षेत्रफल = 4πr²
= 4πx² मी०²
प्रश्नानुसार,
चंद्रमा का व्यास = \(\frac{2 x}{4}\) = मी०
चंद्रमा की त्रिज्या = \(\frac{2 x}{2 \times 4}=\frac{x}{4}\) मी०
∴ चंद्रमा का पृष्ठीय क्षेत्रफल = 4πr²
= 4π × \(\frac{x}{4} \times \frac{x}{4}\) मी०²
= \(\frac{\pi x^2}{4}\) मी०²
चंद्रमा और पृथ्वी के पृष्ठीय क्षेत्रफलों का अनुपात = \(\frac{\pi x^2}{4}: \frac{4 \pi x^2}{1}\)
= πx² : 16πx²
= 1 : 16 उत्तर

प्रश्न 8.
एक अर्धगोलाकार कटोरा 0.25 सें०मी० मोटी स्टील से बना है। इस कटोरे की आंतरिक त्रिज्या 5 सें०मी० है। कटोरे का बाहरी वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल : यहां पर,
अर्धगोलाकार कटोरे की अंतः त्रिज्या (r) = 5 सें०मी०
अर्धगोलाकार कटोरे की बाह्य त्रिज्या (R) = 5 + 0.25 = 5.25 सें०मी०
= \(\frac{525}{100}\) सें.मी० = \(\frac{21}{4}\) सें०मी०
अतः अर्धगोलाकार कटोरे का बाह्य वक्र पृष्ठीय क्षेत्रफल = 2πR²
= 2 × \(\frac{22}{7} \times \frac{21}{4} \times \frac{21}{4}\) सें०मी०² = \(\frac{693}{4}\) सें०मी०²
= 173.25 सें०मी०² उत्तर

प्रश्न 9.
एक लंब वृत्तीय बेलन त्रिज्या r वाले एक गोले को पूर्णतया घेरे हुए है (देखिए आकृति)। ज्ञात कीजिए:
(i) गोले का पृष्ठीय क्षेत्रफल,
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल,
(iii) ऊपर (i) और (ii) में प्राप्त क्षेत्रफलों का अनुपात।

हल :

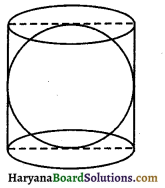
(i) यहां पर,
गोले की त्रिज्या = r
∴ गोले का पृष्ठीय क्षेत्रफल = 4πr² उत्तर

(ii) यहां पर,
बेलन की त्रिज्या = r
बेलन की ऊंचाई = 2r
अतः बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2πr × 2r
= 4πr² उत्तर

(iii) (i) तथा (ii) से प्राप्त क्षेत्रफलों का अनुपात = 4πr² : 4πr²
= 1 : 1 उत्तर