HBSE 10th Class Maths Important Questions Chapter 12 Areas related to Circles

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 12 Areas related to Circles Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 12 Areas related to Circles

Short/Long Answer Type Questions

Question 1.
Find the area of a quadrant of a circle whose circumference is 44 cm.
Solution :
Let the radius of a circle be r cm.
The circumference of a circle = 44 cm (given)

Question 2.
The short hand and long hand of clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 48 hours.
Solution :
The distance travelled by shorthand in 12 hours = 2πr
= 2 × π × 4
[∴ r = 4 cm]
The distance travelled by shorthand in 48 hours = 4 × 8x
= 32πcm
The distance travelled by long hand in 12 hours = 4 × 2лR
= 4 × 2π × 6
[∴ R = 6 cm]
Total distance travelled by their tips in 48 hours = 32π + 48л
= 80π cm.

Question 3.
If the angle of a major sector of a circle is 250°. Then find the angle of minor sector.
Solution :
We have
Angle of major sector = 250°
∴ Angle of minor sector = 360° – 250° = 110°

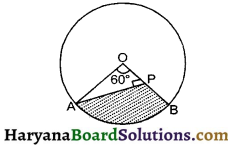
Question 4.
If an arc of a circle subtends an angle of 60° at the centre and if the area of minor sector is 231 cm², then find the radius of the circle.
Solution :
We have sector angle (θ) = 60°
Let radius of circle be r cm
Area of minor sector = 231 cm²

Hence, radius of the circle = 21 cm

Question 5.
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
Solution :
We have
Radius of sector of a circle (r) = 5.2 em
Let sector angle be θ
Perimeter of a sector of a circle = 16.4 cm (given)

Question 6.
Find the area of sector of a circle of radius 6 cm whose central angle is 30°. (take π = 3.14)
Solution :
We have
Radius of a circle (r) = 6 cm
Sector angle (θ) = 30°
Area of a sector = \(\frac{\pi^2 \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 6^2 \times 30^{\circ}}{360^{\circ}}\)
= 3.14 × 3
= 9.42 cm²

Question 7.
In the given figure is a sector of circle of radius 10.5 cm. Find the perimeter of sector.
(Take π = 22/7)

Solution :
We have
Radius of a sector of circle (r) = 10.5 cm
Sector angle (θ) = 60°
Perimeter of sector = \(\frac{2 \pi r \theta}{360^{\circ}}\)
= \(\frac{2 \times 22}{7} \times \frac{10.5 \times 60}{360^{\circ}}\)
= 22 × 0.5
= 11 cm²

Question 8.
In the given figure, AOB is a sector of angle 60° of a circle with centre O and radius 17 cm. If AP ⊥ OB and AP = 15 cm, find the area of shaded region.

Solution :
We have
Radius of circle (r) = AO 17 cm
∠APO = 90° and AP = 15 cm,
sector angle (θ) = 60°
In right triangle AOP
⇒ AO² = AP² + OP²
17² = 15² + OP²
17² – 15² = OP²
(17 + 15) (17 – 15) = OP²
32 × 2 = OP²
OP = \(\sqrt{m}\) = 8 cm
Area of shaded region
= Area of sector AOBA – area of Δ AOP

Question 9.
In the given figure two arcs, A and B. Are A is part of the circle with centre O and radius OP. Arc B is part of the circle with centre M and radius PM, where M is the midpoint of PQ. Show that area enclosed by two arcs is equal to (\(\sqrt{3}\) – \(\frac {π}{6}\)) cm²

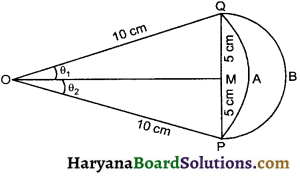
Solution :
We have
Radius of semicircle (PBQ)
R = 5 cm
Area of semicircle (A₁) = \(\frac {1}{2}\)πR²
= \(\frac {1}{2}\) × π × 5²
= \(\frac {25π}{2}\) cm²
Let ∠MOQ = ∠MOP = Q₁
In the right ΔOMQ, we have
sin θ₁ = \(\frac{\mathrm{MQ}}{\mathrm{OQ}}=\frac{5}{10}=\frac{1}{2}\)
sin θ₁ = sin 30°
θ₁ = 30°
∠POQ = 2θ = 2 × 30° = 60°
Area enclosed by are A and chord PQ (A₂)

= 25(\(\sqrt{3}\) – \(\frac {π}{6}\))
So, required area = 25(\(\sqrt{3}\) – \(\frac {π}{6}\))
Hence Proved

Question 10.
Find the area of shaded region in the givem figure, where arcs drawn with centres A, B, C, D intersect in pairs at midpoints P, Q, Rand S of the sides AB, BC, CD and DA respectively of square ABCD of side 12 cm.
[use π = 3.14]

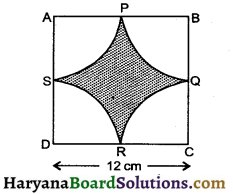
Solution :
We have
side of a square = 12 cm
Area of a square (ABCD)= 12 × 12 = 144 cm²
Radius of each sector (r) = \(\frac {12}{2}\) = 6cm
Each sector angle (θ) = 90°
Area of each sector = \(\frac{\pi r^2 \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 6^2 \times 90}{360^{\circ}}\)
= 3.14 × 9
= 28.26 cm²
Area of 4 sectors = 28.26 × 4
= 113.04 cm²
Area of shaded region
= Area of square – 4 sectors area
= 144 – 113.04
= 30.96 cm²
= 7 cm

Question 11.
In the adjoining figure ABCD is a trapezium with AB || DC and ∠BCD = 30°. In figure BGEC is a sector of a circle with centre C and AB = BC = 7 cm, DE = 4 cm and BF = 3.5 cm, find the area of the shaded region. [use x = \(\frac {22}{7}\)]

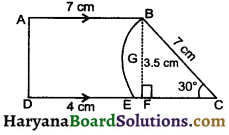
Solution :
We have
AB = 7 cm, DE = 4 cm and BF = 3.5 cm
DC= DE + EC = 4 + 7 = 11 cm
Area of trapezium ABCD
= \(\frac {1}{2}\)(AB + DC) × BF
= \(\frac {1}{2}\)(7 + 11) × 3.5
= 9 × 3.5
= 31.5 cm²
Area of sector BGEC = \(\frac {θ}{360°}\) πr²
= \(\frac {30°}{360°}\) × \(\frac {22}{7}\) × 7²
= \(\frac{22 \times 7}{12}\)
= 12.83 cm²
Area of shaded region = Area of trapezium – sector area
= 31.5 – 12.83
= 18.67 cm²

Question 12.
The side of a square is 10 cm, find the area between inscribed and circumscribed circle of the square.

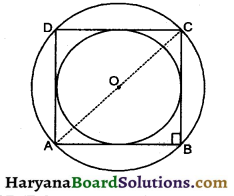
Solution:
Let ABCD be a square of side 10 cm
Radius of inscribed circle (r) = 5 cm
∴ Area of inscribed circle (A₁) = πr²
= π × 5²
= 25π cm²
In right ΔABC, we have
AC² = AB² + BC²
AC² = 10² + 10²
AC² = 100 + 100
AC = 200
AC = \(\sqrt{2 \times 10 \times 10}\) = 10\(\sqrt{2}\) cm
Radius of circumscribed circle (R) = \(\frac{10 \sqrt{2}}{2}\)
= 5\(\sqrt{2}\)
Area of a circumscribed circle (A₂) = πR²
= π × (5\(\sqrt{2}\))²
= 50π
Required area = A₂ – A₁
= 50π – 25π
= 25π cm²

Question 13.
In the give figure, the boundary of the shaded region consists of four semicircular ares, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find.
(i) length of the boundary
(ii) the area of the shaded region.

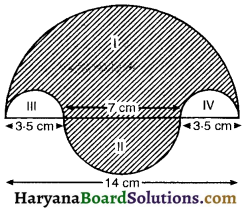
Solution :
We have,
Diameter of the biggest circle = 14 cm
∴ radius of the biggest circle (r₁) = \(\frac {14}{2}\) = 7 cm and diameter of the smallest circle = 3.5 cm
∴ radius of the two smallest circle (r₂) = \(\frac {3.5}{2}\)
and radius of the circle (II) = r₃ = \(\frac {7}{2}\) = 3.5 cm
(i) length of the boundary = πr₁ + 2 × πr₂ × πr₃
= \(\frac {22}{7}\) × 7 + 2 × \(\frac {22}{7}\) × \(\frac {3.5}{2}\) + \(\frac {22}{7}\) × 3.5
= \(\frac {22}{7}\) [7 + 3.5 + 3.5]
= \(\frac {22}{7}\) × 14
= 44 cm

(ii) The area of the shaded region

Hence, (i) length of the boundary = 44 cm
(ii) Area of the shaded region = 86.625 cm²

Question 14.
In the given, the side of square is 28 cm, and radius of each circle is half of the length of the side of the square, where O and O’ are centers of the circle. Find the area of shaded area.

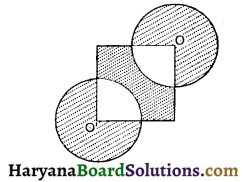
Solution :
Side of the square = 28 cm (given)
∴ Area of sqaure = 28 × 28 = 784 cm²
∴ Radius of each circle is half of the length of the side of the square (given)
∴ Radius of each circle (r) = \(\frac {1}{2}\) × 28 = 14cm
Area of two circles = 2πr²
= 2 × \(\frac {22}{7}\) × 14²
= 44 × 2 × 14
= 1232 cm²
Area of two quadrants = 2 × \(\frac{\pi r^2 \theta}{360^{\circ}}\)
= 2 × \(\frac {22}{7}\) × \(\frac{14^2 \times 90}{360}\)
= 44 × 7
= 308 cm²
Area of shaded region = Area of square + area of two circles – area of two quadrants
= 784 + 1232 – 308
= 1708 cm²

Question 15.
In the given figure, Δ ABC is right angles triangle in which ∠A = 90°. Semicircles are drawn on AB, AC and BC as diameters. Find the area of shaded region.

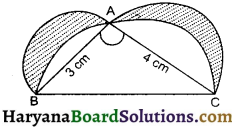
Solution :
In Δ ABC, we have
∠A = 90°, AB = 3 cm, AC = 4 cm
BC² = AB² + AC²
[By Pythagoras theorem]
⇒ BC² = 3² + 4²
= 9 + 16 = 25
BC = 5 cm
Area of semicircle with radius \(\frac {3}{2}\) cm (A₁)
= \(\frac {1}{2}\)π × (\(\frac {3}{2}\))² = \(\frac {9}{8}\)π cm²
Area of semicircle with radius \(\frac {4}{2}\) cm (A₂)
= \(\frac {1}{2}\)π × 2² = \(\frac {4π}{2}\)་cm²
Area of semicircle with radius \(\frac {5}{2}\) cm (A₃)
= \(\frac {1}{2}\)π × (\(\frac {5}{2}\))²
= \(\frac {25}{8}\)π cm²
Area of right triangle ABC = \(\frac {1}{2}\) × 3 × 4 = 6cm²
area of shaded region = A₁ + A₂ – (A₃ – A₄)

Question 16.
Sides of a triangular field are 15 m, 16 m and 17. With the three corners of the field a cow, a uffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Solution :
We have,
Radius of each sector is = 7 m
Sides of triangle are 15 m, 16 m and 17 m respectively.
Let a cow, a buffalo and a horse are tied respectively with vertex A, B and C separately.
Let ∠A = x₁°, ∠B = x₂°, ∠C = x₃°
The area of the field which can graze by three animals Sum of the areas of three sectors with sector angles x₁°, x₂°, x₃° and radius 7m.

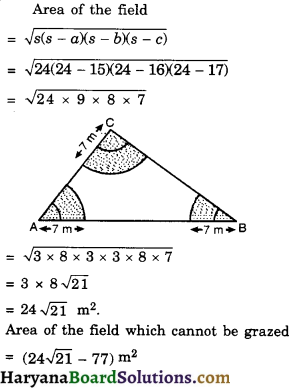
Question 17.
In the adjoining figure, O is the centre and BOC is the diameter of the circle. Find the area of the shaded region. (use π = 3.14)

Solution :
We have,
AB = 6 cm, AC = 8 cm and BOC is the diameter of the circle.
In right ΔBAC,
BC² = AB² + AC²
[By Pythagoras theorem]
BC² = 6² + 8²
BC² = 36 + 64
BC² = 100
BC = \(\sqrt{100}\) = 10 cm.
Radius of the circle = \(\frac {10}{2}\) = 5 cm.
Therefore,
OP = OQ = 5 cm
(equal radii of the circle)
Shaded region area = Semi-circle area drawn as BC diameter – ΔABC area + segment PRQ area
= \(\frac {1}{2}\)π × (5)² – \(\frac {1}{2}\) × 6 × 8 + area of quadrant POQ – area of ΔPOQ
= \(\frac {1}{2}\) × 3.14 × 25 – 24 + \(\frac {1}{4}\)π × (5)² – \(\frac {1}{2}\) × 5 × 5
= 39.25 – 24 + \(\frac {1}{4}\) × 3.14 × 25 – 12.5
= 15.25+ 19.625 – 12.5
= 34.875 – 12.5
= 22.375 = 22.38 cm². (approx)
Hence, area of shaded region = 22.38 cm².
(approx)

Fill in the Blanks

Question 1.
The region between an are and the ……….. joining the centre to the end points of the arc is called a sector of the circle.
Solution :
Two raddi

Question 2.
A ……….. of a circle is a line segment joining any two points on the circle.
Solution :
chord

Question 3.
The length of the complete circle is called its……….
Solution :
circum- ference

Question 4.
The region between a chord and either of its …………. is called a segment of the circle.
Solution :
src

Question 5.
The cicles which have same centre and different …………. are called concentric circle.
Solution :
raddi

Question 6.
If the perimeter of a circle is equal to that of a square, then the ratio of their areas is ……..
Solution :
14 : 11

Multiple Choice Questions

Choose the correct answer for each of the following :

Question 1.
The circumferences of two circles are in the ratio 3 : 4. The ratio between their areas is:
(a) 9 : 4
(b) 16 : 9
(c) 3 : 4
(d) 9 : 16
Solution :

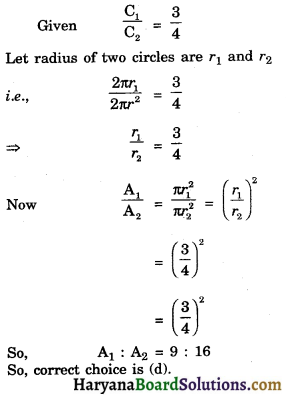
Question 2.
The areas of two circles are in the ratio 16 : 25. The ratio of their circumference is:
(a) 4 : 5
(b) 5 : 4
(c) 16 : 25
(d) 25 : 16
Solution :

Question 3.
The area of a circle is 13.86 cm², the circumference of the circle is :
(a) 13.6 cm
(b) 13.2 cm
(c) 6.6 cm
(d) 13.4 cm
Solution :
(b) 13.2 cm

Given, area of circle 13.86 cm²
⇒ πr² = 13.86
3.14 r² = 13.86
r² = \(\frac {13.86}{3.14}\)
r = 2.1 cm
∴ circumference = 2πr
= 2 × \(\frac {22}{7}\) × 2.1
= 13.2 cm
So correct choice is (b).

Question 4.
Area of the largest triangle that can be inscribed in a semicircle of radius r units is :
(a) r² sq. units
(b) \(\frac {1}{2}\)r² sq. units
(c) 2r² sq. units
(d) \(\sqrt{2}\)r² sq. units
Solution :
(a) r² sq. units

Area of triangle = \(\frac {1}{2}\)base × height

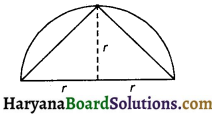
= \(\frac {1}{2}\) × 2r × r
= r² sq. units.
Hence correct choice is (a).

Question 5.
The area of sector of central angle of a circle with radius 4r is:

Solution :
Area of sector = \(\frac{\pi r^2 \theta}{360^{\circ}}\)
= \(\frac{\pi(4 r)^2 x}{360}\)
= \(\frac{2 \pi \cdot x r^2}{45^{\circ}}\)
Hence, correct choice is (b).

Question 6.
If the sum of the circumference of two circles with radii R₁ and R₂ is equal to the circumference of a circle of radius R, then :
(a) R₁ + R₂ = R
(b) R₁ + R₂ > R
(c) R₁ + R₂ < R
(d) Nothing definite can be said about the relation among R₁, R₁ and R.
Solution :
(a) R₁ + R₂ = R

2πR = 2πR₁ + 2πR₂
2πR = 2 × (R₁ + R₂)
R = R₁ + R₂
Hence correct choice is (a).

Question 7.
If the perimeter of circle is equal to that of a square, then ratio of their area is
(a) 22 : 7
(b) 14 : 11
(c) 7 : 22
(d) 11 : 14
Solution :
(b) 14 : 11

Perimeter of circle = 2πr
Perimeter of square = 4a
A.T.Q. 2π = 4a
side of square a = \(\frac {πr}{2}\)

So required ratio = 14: 11
So correct choice is (b).

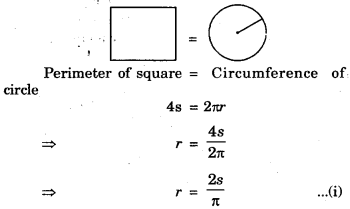
Question 8.
If the circumference of a circle and the perimeter of a square are equal, then :
(a) Area of circle = Area of the square
(b) Area of circle > Area of the square
(c) Area of circle < Area of the square
(d) Nothing definite can be said about the relation between the areas of the circle and square
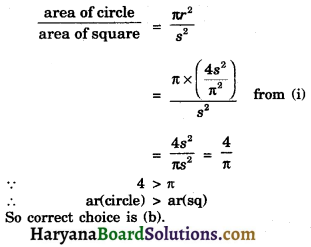
Solution :