Haryana State Board HBSE 9th Class Maths Notes Chapter 13 Surface Areas and Volumes Notes.
Haryana Board 9th Class Maths Notes Chapter 13 Surface Areas and Volumes
Introduction
So far, in all our study, we have been dealing with figures that can be easily drawn on page of our note book or blackboards. These are called plane figures. In previous classes, we have learnt about the perimeters and areas of rectangles, squares, rhombus and circles. If we cut out many of these plane figures of same shape and size from cardboard sheet and stack them up in a vertical pile, then by this process, we will obtain some solid figures such as a cuboid, a cylinder etc. In this chapter, we will learn to find the surface areas and volumes of cubes, cuboids, cylinders, cones and spheres.

Units measurement of Area:
1 km2 = 1 km × 1 km = 10 hm × 10 hm = 100 hm2 or 100 hectares
1 hm2 = 1 hm × 1 hm = 10 dam × 10 dam = 100 dam2
1 hm2 = 1 hm × 1 hm = 100 m × 100 m = 10000 m2
1 dam2 = 1 dam × 1 dam = 10 m × 10 m = 100 m2
1 m2 = 1m × 1m = 10 dm × 10 dm = 100 dm2
1 m2 = 1m × 1m = 100 cm × 100 cm = 10000 cm2
1 dm2 = 1 dm × 1 dm = 10 cm × 10 cm = 100 cm2
1 cm2 = 1 cm × 1 cm = 10 mm × 10 mm = 100 mm2
1 km2 = 1 km × 1 km = 1000 m × 1000 m = 106 m2
1m2 = 1m × 1m = 1000 mm × 1000 mm = 106 mm2
![]()
Units measurement of volume:
1 km3 = 1 km × 1 km × 1 km = 1000 m × 1000 m × 1000 m = 109 m3
1 km3 = 1 km × 1 km × 1 km = 10 hm × 10 hm × 10 hm = 1000 hm3
1 hm3 = 1 hm × 1 hm × 1 hm = 10 dam × 10 dam × 10 dam = 1000 dam3
1 hm3 = 1 hm × 1 hm × 1 hm = 100 m × 100 m × 100 m = 106 m3
1 dam3 = 1 dam × 1 dam × 1 dam = 10 m × 10 m × 10 m = 1000 m3
1 m3 = 1 m × 1 m × 1 m = 100 cm × 100 cm × 100 cm = 106 cm3
1 m3 = 1 m × 1 m × 1 m = 1000 mm × 1000 mm × 1000 mm = 109 mm3
1m3 = 1m × 1m × 1m = 10 dm × 10 dm × 10 dm = 1000 dm3
1 cm3 = 1 ml = 1 cm × 1 cm × 1 cm = 10 mm × 10 mm × 10 mm = 1000 mm3
1 litre = 1000 ml = 1000 cm3
1 m3 = 106 cm3 = 1000 litre = 1 kilolitre
Key Words:
→ Solids: Bodies which have three dimensions in space are called solids.
→ Volume: The amount of space occupied by a solid or bounded by a closed surface is known as the volume of solid.
→ Surface area: Surface area is the total sum of all the areas of all the shapes that cover the surface of solid.
→ Lateral surface area: Lateral surface in a solid is the sum of surface areas of all its faces excluding the bases of solid.
→ Cubold: A cuboid is a solid bounded by six rectangular plane regions.
→ Cube: When all the edges of cuboid are equal in length, it is called a cube.
→ Right circular cylinder: If a rectangle is revolved about one of its sides, the solid thus formed is called a right circular cylinder.
→ Right circular cone: If a right angled triangle is revolved about one of the sides containing a right angle, the solid thus generated is called a right circular cone.
→ Sphere: The set of all points in space which are equidistant from a fixed point, is called a sphere.
→ Hemisphere: A plane through the centre of a sphere divides the sphere into two equal parts. Each part is called a hemisphere.
![]()
Basic Concepts
Surface Area of a Cuboid and a Cube:
(a) Cuboid: A solid bounded by six rectangular faces is called a cuboid.
e.g., a book, a brick, a matchbox, a tile etc. A cuboid has 6 rectangular faces, 12 edges and 8 vertices.
6 rectangular faces are ABCD, EFGH, BCGF, ADHE, ABFE and DCGH.
ABCD is the bottom face and EFGH is the top face and these are one pair of opposite faces. Similarly, other pairs of opposite faces are BCGF, ADHE and ABFE, DCGH.
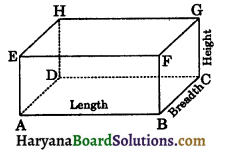
Out of these six faces, BCGF, ADHE, ABFE and DCGH are called the lateral faces of the cuboid. Any two faces other than the opposite faces are called adjacent faces.
In the given figure, ABCD and ABFE are adjacent faces.
Similarly, EFGH and ADHE are adjacent faces.
AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG and DH are 12 edges of a cuboid. A, B, C, D, E, F, G and H are its 8 vertices.
(i) Total surface area of a cuboid:
Area of the face ABCD = Area of the face EFGH = (1 × b) sq. units
Area of the face BCGF = Area of the face ADHE = (b × h) sq. units
Area of the face ABFE = Area of the face DCGH = (1 × h) sq. units
Total surface area of the cuboid = Sum of the areas of six faces
= 2(l × b) + 2(b × h) + 2(l × h).
= 2(l × b + b × h + h × l)
= 2(lb + bh + hl) sq. units
where l = length, b = breadth and h = height.
(ii) Lateral surface area of the cuboid: Out of the six faces of a cuboid, we only find the area of the four faces, leaving the bottom and top faces. In such a case, area of these four faces is called the lateral surface of the cuboid.
Lateral surface area of the cuboid = Area of face BCGF+ Area of face ADHE + Area of face ABFE + Area of face DCGH
=bxh+bxh+lxh+lxh
= 2(l × h) + 2(b × h)
=2(l + b) × h sq. units
= Perimeter of the base × height.
(iii) Diagonal of a cuboid = \(\sqrt{l^2+b^2+h^2}\) units
(b) Cube: A cuboid whose length, breadth and height are all equal is called a cube eg., ice cubes, dice etc.
Each edge of a cube is called its edge. A cube has six faces, All the six faces of a cube are congruent square faces. Length of each edge of the cube is same. It has also 12 edges and 8 vertices.
(i) Total surface area of the cube : Total surface area of the cube is the sum of the areas of the six congruent square faces. Area of the one face is a3, where a is the edge of a cube.
∴ Total surface of the cube = 6a3 sq. units
(ii) Lateral surface area of the cube = 4a3 sq. units
Diagonal of the cube = \(\sqrt{3}\)a units
![]()
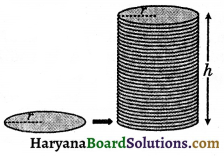
(a) Right Circular Cylinder: If we take a number of circular sheets of paper and stack them vertical pile, we will get a solid called a right circular cylinder.

eg., circular pipes, circular pillars, road rollers, gas cylinders, measuring jars etc. In case if circular sheets are not stack up vertically as shown figure 13.8 (I) then the cylinder is not a right circular cylinder. Of course, if we have a cylinder with a non-circular base as shown in figure 13.8 (II), then we also cannot call it a right circular cylinder.

Remarks: 1. From now onwards, the word cylinder would mean a right circular cylinder.
(b) Some Terms Related to the Cylinder:
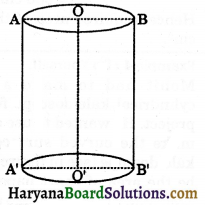
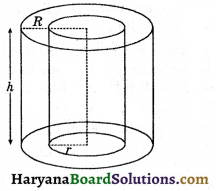
(i) Base: Two circular ends of cylinder are called its bases.
(ii) Radius: The radius of the circular bases is called the radius of the cylinder. In the adjoining figure AO, OB, A’O’ and O’B’ are equal radii of the cylinder.
(iii) Axis: A line segment joining the centres of two circular bases is the called the axis of the cylinder.
In the figure 13.9, OO’ is the axis of the cylinder.
(iv) Height: The length of the axis of the right circular cylinder is called the height of the cylinder. In the figure, OO’ is the height of the cylinder.
(c) Surface Area of Right Circular Cylinder:
(i) Lateral surface area of right circular cylinder: We take a rectangular sheet of paper, whose length is just enough to go round the cylinder and whose breadth is equal to the height of the cylinder as shown figure below.

If we fold rectangular sheet along its length, we get a right circular cylinder of height h. Lateral surface area of the cylinder is the area of the rectangular sheet. The length of the sheet is equal to the circumference of the circular base which is equal to 2πr. Lateral surface area of a cylinder is also called the curved surface area of the cylinder.
Lateral or curved surface area of the cylinder = Area of the rectangular sheet
= length × breadth
=2πr × h = 2πrh sq. units
Therefore, lateral surface area of a cylinder = 2πrh sq. units.
(ii) Total surface area of the right circular cylinder: If we include areas of top and bottom of the cylinder to its lateral surface area, we get the total surface area of the cylinder.
If r is the radius of the cylinder and h its height.
∴ Total surface area of the cylinder = lateral surface area + 2 bases area
= 2πrh + 2πr2[∵ base area = πr2]
= 2πr(h + r) sq. units
Therefore, total surface area of the cylinder = 2πr(h + r) sq. units
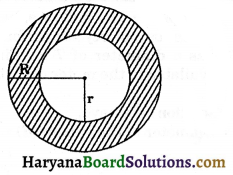
(d) Surface Area of Hollow Cylinder: Hollow cylinder is a solid bounded by two coaxial cylinders of the same height and different radii.
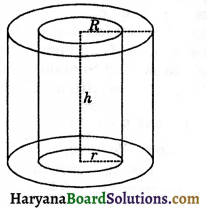
eg., iron pipes, rubber tubes etc.
Let external and internal radii of a hollow cylinder be R and r and h be its height as shown in the given figure.
(i) Area of each base = π(R2 – r2) sq, units
(ii) Lateral or curved surface area of the cylinder = External surface area + Internal surface area
= 2πRh + 2πrh = 2πh(R + r) sq units
(iii) Total surface area of the cylinder
= Lateral surface area + 2 area of the base ring
= 2πh(R + r) + 2π(R2 – r2)
= 2πh(R + r) + 2π(R + r) (R – r)
= 2π(R + r) [h + R – r] sq. units.
![]()
(a) Right Circular Cone: A solid described by the revolution of a right angled triangle about one of its sides (containing the right angle) which remains fixed. In the given figure revolves about side AO. It generates a cone. O is the centre of base BC and A is its vertex.
eg., ice cream cone, clow’s cap, conical vessel etc.
(b) Some Terms Related to the Cone : (i) Radius of the cone: The length segment OB = OC is called radius of the cone. It is usually denoted by r.
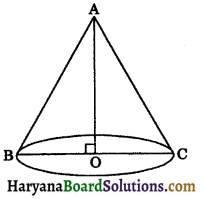
(ii) Height of the cone: The length segment AO is called the height of the cone. It is usually denoted by h.
(iii) Slant height of the cone: Slant height of a right circular cone is the distance of its vertex from any point on the circumference of the base. In the given figure, AB and AC represents the slant height of the cone. It is usually denoted by l.
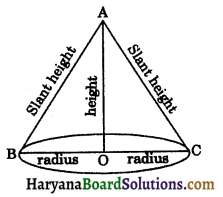
(iv) Vertical angle of the cone: ∠BAC is called the vertical angle of the cone.
(c) Surface Area of a Right Circular Cone: (i) Lateral surface area of a right circular cone: On a sheet of paper, we draw a circle with centre O and radius l. Now cut out a circular region from the sheet of a paper. We obtain a circular disc of paper [see in figure 13.19 (I)].
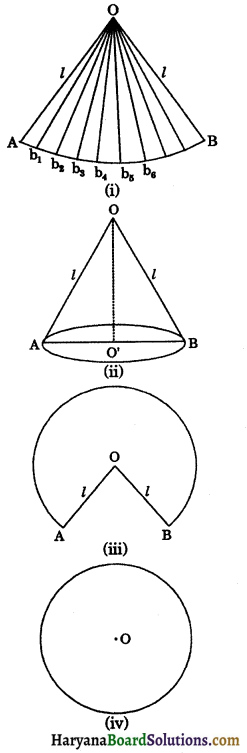
Now cut cone OAB from the circular disc of paper [see figure 13.19 (II, III) and open it out (see in figure 13.19 (IV)]. AB is the perimeter of base of cone OAB. The cone OAB is cut into small pieces of triangles such as ΔOAb1, ΔOb1b2, ΔOb2b3, …… whose height is the slant height of the cone.
Area of each small triangle = \(\frac{1}{2}\)base of each triangle × l
Area of entire piece of paper (cone ΔOAB) = Sum of the areas of all triangles
= \(\frac{1}{2}\)b1l + \(\frac{1}{2}\)b2l + \(\frac{1}{2}\)b3l + ……..
= \(\frac{1}{2}\)l(b1 + b2 + b3 + ………)
\(\frac{1}{2}\) × l × AB
\(\frac{1}{2}\)l × 2πr = πrl
So, curved surface area of a cone = πrl.
(ii) Total surface area of a right circular cone:
Total surface of the cone = Lateral surface area + Area of the base of a cone
= πrl + πr2 = πr(l + r)
So, total surface area of the cone = πr(l + r),
where r is its base radius and l its slant height.
(iii) Relation between the height, slant height and radius of cone:
l2 = h2 + r2
⇒ l = \(\sqrt{h^2+r^2}\)
![]()
1. (a) Sphere: A sphere is a solid described by the revolution of a semicircle about its diameter, which remains fixed, e.g., football, volleyball, throwball, etc.
In the given figure 13.27 (i) semicircle ABC by revolving about its diameter AB describes the sphere [(see in figure 13.27 (ii)]
The mid point of AB is the centre. Any line which passes through the centre and is terminated both ways by the surface is a diameter. Any line drawn from the centre to the surface is known as radius. A sphere may also defined as:

A sphere is a three dimensional figure (solid figure) which is made up of all points in the space, which lie at a constant distance from a fixed point is called the radius and the fixed point called the centre of the sphere.
(b) Surface Area of a Sphere: Let us take a rubber ball and drive a nail into it. Let us wind a string around the ball. When you reached the fullest part of the ball, use pins to keep the string in place and continue to wind the string around the remaining part of the ball till it is fully covered [see in figure 13.28 (I) and (II)].
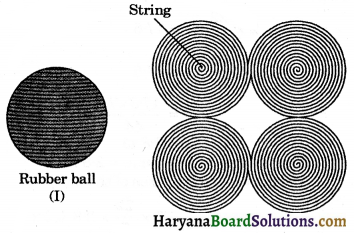
Now, we unwind the string from the surface of the ball.
Start filling the circles one by one, with the string you had wound around the wall (see fig. 13.28). Then, on a sheet of paper, we draw four circles with radius equal to the radius of the ball. Now string is used to completely fill the regions of four circles, all of the same radius as of the sphere. It means, the surface area of a sphere of radius r = 4 times the area of a circle of radius r.
Therefore,surface area of sphere = 4πr2.
2. Hemisphere: A plane through the centre of a sphere divides the sphere into two equal parts. Each part is called a hemisphere.
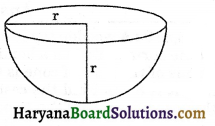
For a hemisphere of radius r, we have
(i) Curved surface area of the hemisphere = 2πr2
(ii) Total surface area of the hemisphere
= 2πr2 + πr2
= 3πr2.
3. (a) Spherical Shell: The difference of two solid concentric spheres is called a spherical shell.
(b) Surface Area of Spherical Shell: If R and be the external and internal radii of a spherical shell, then
Total surface area of spherical shell = 4π(R2 + l2).
![]()
1. Volume of a Cuboid: In previous classes, we have learnt about of certain figures. Recall that solids occupy space. The measure of this occupied space is called the volume of the object.
If the object is hollow, then interior is empty and can be filled with air or some liquid that will take the shape of its container. In this case, the volume of the substance that can fill the interior is called the capacity of the container. Thus, we may say that the volume of an object is the measure of the space it occupies and the capacity of an object is the volume of substance its interior can accommodate. Unit of measurement of volume is cubic unit. If we take some rectangular sheets and place it one over the other. If we place these sheets vertically in pile, we get a cuboid. (see figure below)

If area of each rectangle is A, the height upto which the rectangles are stacked is h. Measure of the space occupied by the cuboid
= Area of a rectangular sheet × height
= A × h = l × b × h [∵ A = l × b]
Hence, volume of the cuboid = l × b × h
= length × breadth × height
Also, volume of the cuboid = Area of the base × height
2. Volume of Cube: If length, breadth and height of a cuboid are equal, then it is known as the cube.
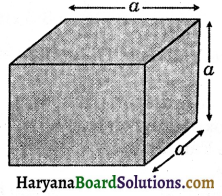
Volume of a cube = edge × edge × edge
= a × a × a = a3,
where a is the edge of a cube. Unit of measurement of volume is cubic unit.
![]()
(a) Volume of a Cylinder: If we stack the circular sheets of radius r vertically, we will get a solid called a right circular cylinder of radius r and height h.
Volume of the cylinder = The area of each circular sheet × height
= πr2 × h = πr2h
or Volume of the cylinder = Area of the base × height
= πr2h.
(b) Volume of the Hollow Cylinder: Let the external and internal radii of the hollow cylinder be R and r respectively and h be its height, then
Volume of the material = External volume – Internal volume.
= πR2h – πr2h
= πh(R2 – r2).
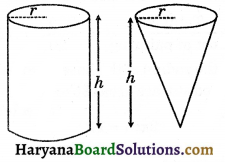
Volume of a Right Circular Cone:
Experiment: Take a hollow cylinder and a hollow cone of the same base radius and the same height.
Fill the cone with water to the brim and empty it into the cylinder. Repeat the process two times more. We observe that 3 cone full to brim will fill the cylinder competely. With this, we can safely come to the conclusion that three times the volume of a cone, makes up the volume of a cylinder.
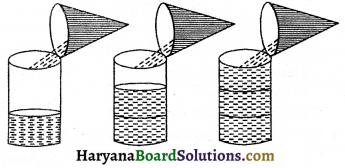
It means volume of a cone of radius ‘r’ and height ‘h’
= \(\frac{1}{3}\) of volume of cylinder of radius ‘r’ and height ‘h’
Volume of a cone = \(\frac{1}{3}\) × πr2h
or Volume of a cone = \(\frac{1}{3}\) × Area of the base × height
![]()
1. Volume of a Sphere: We take a cylindrical container and two or three spheres of different radii. Also take a large trough in which we can place the cylindrical container. Then fill the container up to the brim with water.
Now, we place a sphere in the container. Some of the water will overflow into the trough in which it is kept (see in figure given below).
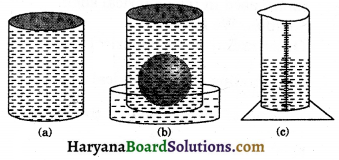
We pour out the water from the trough into a measuring cylinder and find the volume of the over flowed water. If r is the radius of immersed sphere on evaluating \(\frac{4}{3}\)πr3, we find this value atmost equal to the volume of over flowed water.
We repeat this process with two or three spheres of different radii, we find:
Volume of overflowed water = The volume of the sphere immersed in the water
= \(\frac{4}{3}\)πr3
Thus,volume of the sphere = \(\frac{4}{3}\)πr3.
2. Volume of the hollow sphere: If R and r are respectively the outer and inner radii of hollow sphere.
Volume of the material = Volume of outer sphere – Volume of inner sphere
= \(\frac{4}{3}\)πrR3 – \(\frac{4}{3}\)πr3
= \(\frac{4}{3}\)π(R3 – r3)
3. Volume of the hemisphere :
Volume of the hemisphere \(\frac{2}{3}\)πr3
where r is the radius of the hemisphere.