HBSE 8th Class Maths Solutions Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Intext Questions

Haryana State Board HBSE 8th Class Maths Solutions Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Intext Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Intext Questions

(प्रयास कीजिए – पृष्ठ 146)

प्रश्न 1.
एक चर वाले और दो चरों वाले व्यंजकों के पाँच-पाँच उदाहरण दीजिए।
हल:
एक चर वाले व्यंजक के पाँच उदाहरण x + 6, x – 6, 6 + y, 7 – y और 4 + 3x
दो चरों वाले व्यंजकों के पाँच उदाहरण- x + 6y, x – 2y, 4x + y, 2x – y और 3x + 2y

प्रश्न 2.
x, x – 4, 2x + 1, 3x – 2 को संख्या रेखा पर दर्शाइए।
हल:
व्यंजक x का निरूपण-
माना संख्या रेखा पर चर x की स्थिति x है तो X, x को प्रदर्शित करता है जैसा आकृति में दिया है-

व्यंजक x – 4 का निरूपण-
माना स्थिति X चर x को प्रदर्शित करती है।
यहाँ हम एक बिन्दु P चाहते हैं जो x से 4 कम हो। अतः x से आरम्भ करके यह बिन्दु X की बाईं ओर 4 इकाई दूरी पर होगा, जैसा कि आकृति में दिखाया गया है।

2x + 1 का निरूपण-

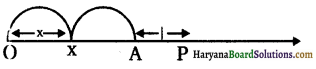
माना चर x की संख्या रेखा पर स्थिति x है। 2x की स्थिति बिन्दु A पर इस प्रकार है
OA = 2 × OX = 2x.
यहाँ, हमें 2x + 1 प्राप्त करना है अर्थात् 2x से एक अधिक। | अतः हम A से प्रारम्भ करेंगे और A के दाएँ 1 इकाई दूरी पर P होगा जो 2x + 1 को प्रदर्शित करता है, जैसा कि आकृति में दिखाया गया है।

व्यंजक 3x -2 का निरूपण-

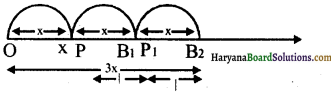
माना संख्या रेखा पर चर x की स्थिति x है। बिन्दु A, पर 3x की स्थिति इस प्रकार है-OA2 = 3 × OX = 3x. यहाँ, हमें 3x – 2 प्राप्त करना है अर्थात् 3x से 2 कम। अतः, हम A, से प्रारम्भ करेंगे और इसके बाएँ 2 इकाई बिन्दु पर P प्राप्त करेंगे जो 3x – 2 को प्रदर्शित करता है, जैसा कि आकृति में दिखाया गया है।

(प्रयास कीजिए – पृष्ठ 146)

प्रश्न 1.
व्यंजक x²y² – 10x²y + 5xy² – 20 के प्रत्येक पद के गुणांक को पहचानिए।
हल:
व्यंजक x²y² – 10x²y² + 5xy² – 20 में x²y² पद में xy का गुणांक 1 है।
– 10xy² पद में ry का गुणांक – 10 है।
5xy² पद में xy² का गुणांक 5 है।

(प्रयास कीजिए – पृष्ठ 146)

प्रश्न 1.
निम्नलिखित बहुपदों को एकपद, द्विपद एवं त्रिपद के रूप में वर्गीकृत कीजिए -z + 5, x + y + z, y + z + 100, ab – ac, 17
हल:
दिए गए बहुपद निम्न प्रकार वर्गीकृत होंगे
एक पद : 17
द्विपद : -z + 5, ab – ac
त्रिपद : x + y + z, y + z + 100

प्रश्न 2.
बनाइए
(a) तीन ऐसे द्विपद जिनमें केवल एक चर x हों।
(b) तीन ऐसे द्विपद जिनमें x और y चर हों।
(c) तीन एकपद जिनमें और y चर हों।
(d) चार अथवा अधिक पदों वाले 2 बहुपद।
हल:
(a) तीन ऐसे द्विपद जिनमें केवल एक चर x हो वे हैं- 2x + 3, 4x + 7, 3 – x
(b) तीन द्विपद जिनमें x और y चर हों वे हैं- x + y, xy – 7, 4x – y.
(c) तीन एकपद, जिनमें x और y चर हों वे हैं xy, 3x²y, – 5xy²
(d) चार या अधिक पद वाले 2 बहुपद हैं-
3x³ – x² + 2x + 3, 4 – 5x + 6x² – 2x³ – 2x⁴

(प्रयास कीजिए – पृष्ठ 147)

प्रश्न 1.
निम्नलिखित में से प्रत्येक के दो समान पद लिखिए
(i) 7xy
(ii) 4mn²
(iii) 2l
हल:
(i) 7xy के दो समान पद हैं 5xy, – 3xy

(ii) 4mn² के दो समान पद हैं 3mn², – 4n²m.

(iii) 2l के दो समान पद हैं 3l, – 4l

(प्रयास कीजिए – पृष्ठ 150)

प्रश्न 1.
क्या आप ऐसी और दो परिस्थितियों के बारे में सोच सकते हैं जहाँ हमें बीजीय व्यंजकों को गुणा करना पड़ सकता है?
संकेत-
(i) एक वस्तु का अंकित मूल्य ₹ (x+2) हैं। इसी प्रकार की (x-5 y)$ वस्तुओं का मूल्य ज्ञात करने के लिये अंकित मूल्य व वस्तुओं की संख्या का गुणा करना पड़ेगा।

(ii) स्कूटर 2y km/hr की रफ्तार से (2x+5) hr के लिये चलता है। स्कूटर द्वारा तय की दूरी ज्ञात करने के लिए स्कूटर की रफ्तार व समय का गुणा करना होगा।

(प्रयास कीजिए – पृष्ठ 151)

प्रश्न 1.
4x × 5y × 72 ज्ञात कीजिए-
सर्वप्रथम 4x × 5y ज्ञात कीजिए और फिर उसे 7z से गणा कीजिए, अथवा सर्वप्रथम 5y × 7z ज्ञात कीजिए और इसे 4x से गुणा कीजिए।
क्या परिणाम एक जैसा है? आप क्या विचार करते हैं? क्या गुणा करते समय क्रम का महत्त्व है?
हल:

4x × 5y × 7z = (4x × 5y) × 7z
= 20xy × 7 = 140xyz

और 4x × 5y ×7z = 4x × (5y × 7z)
= 4x × 35yz = 140xyz
∴ (4x × 5y) × 7z = 4x × (5y × 72) अर्थात् परिणाम एक जैसा है।
अतः एकपदी का गुणन साहचर्य है। अर्थात् हम किसी भी क्रम में गुणा करें क्रम का महत्त्व नहीं है।

(प्रयास कीजिए – पृष्ठ 153)

प्रश्न 1.
गुणनफल ज्ञात कीजिए-
(i) 2x(3x + 5xy)
(ii) a²(2ab – 5c)
हल:
(i) 2x(3x +5xy) = 2x × 3x + 2x × 5xy
= 6x² + 10x²y

(ii) a²(2ab – 5c) = a² × 2ab – a² × 5c
= 2a³b – 5a²c

(प्रयास कीजिए – पृष्ठ 158)

प्रश्न 1.
(4p² + 5p + 7) × 3p का गुणनफल ज्ञात कीजिए।
हल:
(4p² + 5p +7) × 3p = 4p² × 3p + 5p × 3p + 7 × 3p
= 12p³ + 15p² + 21p

(प्रयास कीजिए – पृष्ठ 158)

प्रश्न 1.
सर्वसमिका (I) में b के स्थान पर -b रखिए।क्या आपको सर्वसमिका (II) प्राप्त होती है?
हल:
(a + b)² = a² + 2ab + b² में b = – b रखने पर
(a + (-b))² = a² + 2a(-b) + (-b)²
या (a – b)² = a² – 2ab + b²
अतः सर्वसमिका I में b = – b रखने पर सर्वसमिका II प्राप्त होती है।

(प्रयास कीजिए – पृष्ठ 158)

प्रश्न 1.
a = 2, b = 3, x = 5 के लिए सर्वसमिका (IV) का सत्यापन कीजिए।
[सर्वसमिका IV : (x + a) (x + b) = x² + (a + b)x + ab]
हल:
a = 2, b = 3, x = 5 के लिए
बायाँ पक्ष = (5 + 2) (5 + 3) = (7) (8) = 56
और, दायाँ पक्ष = (5) + (2 + 3) (5) + (2) (3)
= 25 + 25 + 6 = 56
अतः, सर्वसमिका के दोनों पक्षों के मान a = 2, b = 3, x = 5 के लिए समान हैं।

प्रश्न 2.
सर्वसमिका (IV) में a = b लेने पर, आप क्या प्राप्त करते हैं? क्या यह सर्वसमिका (1) से सम्बन्धित है?
हल:
जब a = b तो सर्वसमिका (IV) होगी
(x + b) (x + b) = x² + (b + b)x + (b.b)
या (x+ b) = x² + 2bx + b²
हाँ, यह सर्वसमिका (I) से सम्बन्धित है।

प्रश्न 3.
सर्वसमिका (IV) में a = -c तथा b = -c लेने पर आप क्या प्राप्त करते हैं? क्या यह सर्वसमिका (II) से सम्बन्धित है?
हल:
जब a = – c और b = -c, तो सर्वसमिका (IV) होगी
[(x+ (-c)][x + (-c)] = x² + (-c-c)x + (-c) (-c)
⇒ (x – c) (x – c) = x² + (-2c)x + c²
⇒ (x – c)² = x² – 2cx + c²
हाँ, यह सर्वसमिका (II) से सम्बन्धित है।

प्रश्न 4.
सर्वसमिका (IV) में b = -a लीजिए। आप क्या पाते हैं? क्या यह सर्वसमिका (III) से सम्बन्धित है?
हल:
जब b = – a तो सर्वसमिका (IV) होगी
(x + a) [(x + (-a)], = x² + (a – a)x + (a)(-a)
या (x + a) (x – a) = x² – a²
हाँ, यह सर्वसमिका (III) से सम्बन्धित है।