HBSE 12th Class Physics Important Questions Chapter 2 स्थिर वैद्युत विभव तथा धारिता

Haryana State Board HBSE 12th Class Physics Important Questions Chapter 2 स्थिर वैद्युत विभव तथा धारिता Important Questions and Answers.

Haryana Board 12th Class Physics Important Questions Chapter 2 स्थिर वैद्युत विभव तथा धारिता

वस्तुनिष्ठ प्रश्न-

1. दो समान आवेश q एक-दूसरे से d दूरी पर रखे हैं। इनके मध्य दूरी पर स्थित बिन्दु पर विभव होगा-
(अ) शून्य
(ब) \(\frac{\mathrm{kq}^2}{\mathrm{~d}}\)
(स) \(4 \frac{\mathrm{kq}}{\mathrm{d}}\)
(द) \(\frac{\mathrm{kq}}{\mathrm{d}^2}\)
उत्तर:
(स) \(4 \frac{\mathrm{kq}}{\mathrm{d}}\)

2. पृथ्वी का विद्युत विभव माना गया है-
(अ) धनात्मक
(ब) ऋणात्मक
(स) शून्य
(द) 1000 बोल्ट
उत्तर:
(स) शून्य

3. एक E = 0 वाले विद्युत क्षेत्र की तीव्रता में विद्युत विभव का दूरी के साथ परिवर्तन होगा-
(अ) V ∝ r
(स) V ∝ \(\frac{1}{r}\)
(ब) V ∝ \(\frac{1}{\mathrm{r}^2}\)
(द) V = नियत
उत्तर:
(द) V = नियत

4. एक समबाहु त्रिभुज के तीन कोनों पर समान आवेश स्थित है। त्रिभुज के केन्द्र O पर विद्युत विभव V तथा विद्युत क्षेत्र की तीव्रता E के लिए सत्य कथन होगा-
(अ) V = 0, E = 0
(स) V=0, E≠ 0
(ब) V = 0, E≠ 0
(द) V≠ 0, E = 0
उत्तर:
(द) V≠ 0, E = 0

5. जब दो आवेश के बीच की दूरी बढ़ाई जाती है तो आवेश की स्थितिज ऊर्जा-
(अ) बढ़ती है।
(स) नियत रहती है।
(ब) घटती है।
(द) बढ़ या घट सकती है।
उत्तर:
(द) बढ़ या घट सकती है।

6. यदि एक धन आवेश को निम्न विभव के क्षेत्र से उच्च विभव के क्षेत्र में ले जाया जाता है तो विद्युत स्थितिज ऊर्जा-
(अ) घटती है।
(स) स्थिर रहती है।
(ब) बढ़ती है।
(द) घट भी सकती है अथवा बढ़ भी सकती है।
उत्तर:
(ब) बढ़ती है।

7. दो बिन्दुओं के मध्य की दूरी 30 सेमी. है। यदि बिन्दु A पर 20 µC आवेश व B पर 10C आवेश पर रखा हुआ है तो A व B के बीच किस बिन्दु पर विभव शून्य होगा-
(अ) A से 20 सेमी. दूर
(स) A पर
(ब) B से 20 सेमी. दूर
(द) B पर।
उत्तर:
(अ) A से 20 सेमी. दूर

8. समविभव पृष्ठ में से पारित फ्लक्स हमेशा-
(अ) पृष्ठ के लम्बवत् होता है।
(ब) पृष्ठ के समान्तर होता है।
(स) शून्य होता है।
(द) पृष्ठ से 45° कोण पर होता है।
उत्तर:
(अ) पृष्ठ के लम्बवत् होता है।

9. पानी की आवेशित 64 बूंदों को मिलाकर एक बड़ी बूंद बना ली जाती है तो बड़ी बूंद पर विभव का मान पूर्ण मान से कितने गुना होगा-
(अ) 4 गुना
(ब) 16 गुना
(स) 64 गुना
(द) 8 गुना
उत्तर:
(ब) 16 गुना

10. धातु के एक आवेशित ठोस गोले के केन्द्र पर विद्युत विभव है-
(अ) शून्य
(ब) ठोस गोले की सतह पर विभव से आधा
(स) ठोस गोले की सतह पर विभव के बराबर
(द) ठोस गोले की सतह पर विभव से दुगुना
उत्तर:
(स) ठोस गोले की सतह पर विभव के बराबर

11. जब एक परीक्षण आवेश को किसी विद्युत द्विध्रुव के निरक्ष रेखा के अनुदिश अनन्त से द्विध्रुव के निकट लाया जाता है तो किया गया कार्य होगा-
(अ) धनात्मक
(ब) ऋणात्मक
(स) शून्य
(द) अनन्त
उत्तर:
(स) शून्य

12. किसी माध्यम की परावैद्युताशक्ति 2KV mm^-1 है। 50µm के नमूने में बिना बंधे कितना अधिकतम विभवान्तर स्थापित किया जा सकता है?
(अ) 10000 V
(ब) 1000 V
(स) 100 V
(द) 10 V
उत्तर:
(स) 100 V

13. समविभव पृष्ठ वह है-
(अ) जिसका विभव शून्य हो ।
(ब) जिसके समस्त बिन्दुओं पर विभव समान हो।
(स) जिस पर ऋण विभव विद्यमान हो।
(द) जिस पर धन- विभव विद्यमान हो।
उत्तर:
(ब) जिसके समस्त बिन्दुओं पर विभव समान हो।

14. एक आवेशित गोलाकार चालक के केन्द्र पर विद्युत विभव चालक के तल पर विभव की तुलना में-
(अ) कम होगा
(स) समान होगा
(ब) अधिक होगा
(द) शून्य होगा।
उत्तर:
(स) समान होगा

15. शंकु की आकृति के सुचालक वस्तु का आवेश घनत्व अधिकतम होगा-
(अ) नीचे की चौड़ी सतह पर
(ब) ऊपर की चोटी पर
(स) सम्पूर्ण सतह पर
(द) सिर्फ ऊपर की सतह पर
उत्तर:
(ब) ऊपर की चोटी पर

16. r₁ और r₂ त्रिज्याओं के दो गोलों पर आवेश q इस प्रकार बंटा है कि उनका पृष्ठ घनत्व समान है। उनके विभव में अनुपात –
(अ) \(\frac{\mathrm{r}_1}{\mathrm{r}_2}\)
(ब) \(\frac{r_1^2}{\mathrm{r}_2^2}\)
(स) \(\mathrm{I}_1^3\)
(द) इनमें से कोई नहीं।
उत्तर:
(अ) \(\frac{\mathrm{r}_1}{\mathrm{r}_2}\)

17. विभवान्तर V, आवेश Q तथा धारिता C में सम्बन्ध है-
(अ) V = CQ
(ब) C = VQ
(स) V = \(\frac{Q}{C}\)
(द) Q = \(\frac{\mathrm{V}}{\mathrm{C}}\)
उत्तर:
(स) V = \(\frac{Q}{C}\)

18. समान त्रिज्या के ताँबे के खोखले गोले A व ठोस गोले B को एक समान विभव से आवेशित किया गया है। सत्य कथन है-
(अ) गोले A पर आवेश अधिक होगा
(ब) गोले B पर आवेश अधिक होगा
(स) दोनों पर समान आवेश होगा
(द) निश्चित नहीं कहा जा सकता ।
उत्तर:
(स) दोनों पर समान आवेश होगा

19. एक समान्तर प्लेट संधारित्र को एक बैटरी से आवेशित करके बैटरी हटा ली जाती है। अब संधारित्र की प्लेटों के मध्य दूरी बढ़ा दी जाये तो अब संधारित्र में-
(अ) संधारित्र पर आवेश बढ़ जाता है व धारिता घट जाती है।
(ब) विभवान्तर में वृद्धि तथा धारिता कम हो जाती है।
(स) धारिता बढ़ जाती है।
(द) एकत्रित ऊर्जा के मान में कमी हो जाती है।
उत्तर:
(ब) विभवान्तर में वृद्धि तथा धारिता कम हो जाती है।

20. समान्तर प्लेट संधारित्र की प्लेटों के मध्य के स्थान के आधे भाग में ∈_r, परावैद्युतांक माध्यम भरा हुआ है। यदि हवा वाले भाग की धारिता C है तो सम्पूर्ण संधारित्र निकाय की धारिता होगी-
(अ) \(\frac{2 \epsilon_{\mathrm{r}} \mathrm{C}}{1+\epsilon_{\mathrm{r}}}\)
(ब) \(\frac{C\left(\epsilon_{\mathrm{r}}+1\right)}{2}\)
(स) \(\frac{C \epsilon_{\mathrm{r}}}{1+\epsilon_{\mathrm{r}}}\)
(द) ∈_r
उत्तर:
(स) \(\frac{C \epsilon_{\mathrm{r}}}{1+\epsilon_{\mathrm{r}}}\)

21. तीन संधारित्रों को किस क्रम में जोड़ा जाए कि उनमें समान विभव पर संचित ऊर्जा अधिकतम हो-
(अ) दो समान्तर क्रम में एक श्रेणी क्रम में
(ब) तीनों समान्तर क्रम में
(स) तीनों श्रेणी क्रम में
(द) दो श्रेणी तथा एक समान्तर क्रम में
उत्तर:
(ब) तीनों समान्तर क्रम में

22. छोटी 64 बूँदें मिलकर एक बड़ी बूँद बनाती हैं। यदि प्रत्येक छोटी बूँद पर Q आवेश हो तो बड़ी बूँद पर आवेश होगा-
(अ) 64 Q
(ब) 8 Q
(स) 4 Q
(द) 2 Q
उत्तर:
(अ) 64 Q

23. कम से कम 2 µF धारिता वाले कितने संधारित्र 5 µF धारिता देंगे-
(अ) तीन
(ब) चार
(स) पाँच
(द) सात
उत्तर:
(ब) चार

24. एक संधारित्र की धारिता C है। इसे V विभवान्तर पर आवेशित किया गया है। यदि अब इसे प्रतिरोध से सम्बन्धित कर दिया जाये, ऊर्जा क्षय की मात्रा होगी-
(अ) \(\frac{1}{2}\)CV²
(ब) CV²
(स) \(\frac{\mathrm{CV}^2}{3}\)
(द) \(\frac{1}{2}\)QV²
उत्तर:
(अ) \(\frac{1}{2}\)CV²

25. एक वायु संधारित्र की धारिता 5 µF है। उसी संधारित्र में वायु के स्थान पर पूर्ण रूप से अभ्रक रख दिया जाये तो धारिता 30 µF हो जाती है, अभ्रक का परावैद्युतांक होगा-
(अ) 3
(ब) 6
(स) 12
(द) 24
उत्तर:
(ब) 6

26. 2uF के तीन संधारित्रों को समान्तर क्रम में जोड़ने पर तुल्यधारिता होगी-
(अ) 2μF
(ब) 6μF
(स) \(\frac{1}{3}\)μF
(द) \(\frac{2}{3}\)μF
उत्तर:
(ब) 6μF

27. एक आवेशित समान्तर प्लेट संधारित्र में U, विद्युत ऊर्जा संग्रहित है। संधारित्र की प्लेटों के बीच की दूरी को दुगुना करने पर विद्युत ऊर्जा होगी-
(अ) U。
(ब) \(\frac{\mathrm{U}_0}{2}\)
(स) 2U。
(द) \(\frac{U_0}{4}\)
उत्तर:
(स) 2U。

28. एक समान त्रिज्या एवं समान आवेशयुक्त पानी को 27 छोटी बूंदें मिलकर एक बड़ी बूंद बनाती हैं। बड़ी बूंद की धारिता तथा एक छोटी बूंद की धारिता का अनुपात होगा-
(अ) 2 : 1
(ब) 3 : 1
(स) 4 : 1
(द) 16 : 1
उत्तर:
(ब) 3 : 1

29. दिये गये चित्र में प्रत्येक संधारित्र की धारिता x है बिन्दु A व B के मध्य तुल्यधारिता होगी-

(अ) 3x
(ब) \(\frac{x}{3}\)
(स) \(\frac{2}{3} x\)
(द) \(\frac{3}{2} x\)
उत्तर:
(स) \(\frac{2}{3} x\)

30. 3μF धारिता प्राप्त करने के लिए 2μF के तीन प्रकार संयोजित करेंगे?
(अ) तीनों को समान्तर क्रम में
(ब) तीनों को श्रेणीक्रम में
(स) दो संधारित्र श्रेणीक्रम में तथा तीसरा संधारित्र संयोजन के समान्तर क्रम में
(द) दो संधारित्र समान्तर क्रम में तथा तीसरा संधारित्र संयोजन के श्रेणीक्रम में।
उत्तर:
(स) दो संधारित्र श्रेणीक्रम में तथा तीसरा संधारित्र संयोजन के समान्तर क्रम में

31. संधारित्र में ऊर्जा किस स्वरूप में उपस्थित होती है?
(अ) आवेश के रूप में
(ब) धारिता के रूप में
(स) विद्युत क्षेत्र के रूप में
(द) ऊष्मीय ऊर्जा के रूप में
उत्तर:
(स) विद्युत क्षेत्र के रूप में

32. तीन संधारित्र जिनकी धारिताएँ क्रमश: 2, 4 व 8 μF हैं। पहले श्रेणीक्रम में फिर समान्तर क्रम में जोड़े जाते हैं। दोनों स्थितियों में इनकी तुल्यधारिताओं का अनुपात होगा-
(अ) 49 : 4
(ब) 3 : 7
(स) 4 : 49
(द) इनमें से कोई नहीं।
उत्तर:
(ब) 3 : 7

33. दो संधारित्र जिनकी धारिताएँ C₁ व C₂ हैं। यदि उन्हें समान आवेश दिये जायें तो उनमें संग्रहित ऊर्जाओं का अनुपात होगा-
(अ) \(\frac{\mathrm{C}_2}{\mathrm{C}_1}\)
(ब) \(\frac{\mathrm{C}_1}{\mathrm{C}_2}\)
(स) \(\sqrt{\frac{C_2}{C_1}}\)
(द) \(\sqrt{\frac{C_1}{C_2}}\)
उत्तर:
(अ) \(\frac{\mathrm{C}_2}{\mathrm{C}_1}\)

34. 10μF धारिता के समान्तर प्लेट संधारित्र को 40μc आवेश देने पर उसकी कुल ऊर्जा का मान जूल में होगा-
(अ) 8 × 10^-5
(ब) 800
(स) 8.00
(द) 2 × 10^-3
उत्तर:
(अ) 8 × 10^-5

35. 5 माइक्रो फैरड धारिता के एक आवेशित किया जाता है। संधारित्र पर संचित ऊर्जा होगी-(जूल में)
(अ) 2.5 × 10^-3
(ब) 5.5 × 10^-3
(स) 2.5
(द) 5.0 × 10⁸
उत्तर:
(स) 2.5

36. दो संधारित्रों की धारितायें C₁ तथा C₂ में संग्रहित ऊर्जायें समान हैं। संधारित्रों पर विभवान्तर का अनुपात होगा-
(अ) C₂ : C₁
(ब) \(\sqrt{C_2}: \sqrt{C_1}\)
(स) C₁ : C₂
(द) \(\sqrt{C_1}: \sqrt{C_2}\)
उत्तर:
(ब) \(\sqrt{C_2}: \sqrt{C_1}\)

37. निम्नांकित परिपथ में तुल्यधारिता है-
(अ) \(\frac{5}{3}\) μF
(ब) \(\frac{3}{5}\) μF
(स) 15μF
(द) \(\frac{1}{15}\) μF

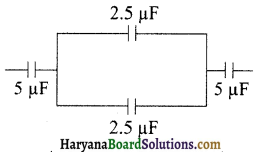
उत्तर:
(अ) \(\frac{5}{3}\) μF

38. संलग्न चित्र में बिन्दुओं A व B के बीच तुल्य धारिता का मान होगा-

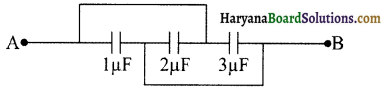
(अ) 6μF
(ब) 4μF
(स) \(\frac{6}{11}\)
(द) \(\frac{11}{5}\)
उत्तर:
(अ) 6μF

39. आवेशित संधारित्र में संग्रहित ऊर्जा होती है-
(अ) धन आवेशित प्लेट पर
(ब) धन तथा ऋण आवेशित दोनों प्लेटों पर
(स) प्लेटों के मध्य क्षेत्र में
(द) संधारित्र के किनारे पर
उत्तर:
(स) प्लेटों के मध्य क्षेत्र में

40. C₁ तथा C₂ धारिता के दो संधारित्रों के समान्तर संयोजन को Q आवेश दिया जाता है। C₁ पर Q₁ तथा C₂ पर Q₂ आवेश होने पर \(\frac{\mathrm{Q}_1}{\mathrm{Q}_2}\) का अनुपात होगा-
(अ) \(\frac{\mathrm{C}_2}{\mathrm{C}_1}\)
(ब) \(\frac{C_1}{C_2}\)
(स) \(\frac{\mathrm{C}_1 \mathrm{C}_2}{1}\)
(द) \(\frac{1}{\mathrm{C}_1 \mathrm{C}_2}\)
उत्तर:
(ब) \(\frac{C_1}{C_2}\)

41. समान्तर प्लेट संधारित्र की धारिता का मान कम करने के लिए प्लेटों के बीच रिक्त स्थान-
(अ) में परावैद्युत पदार्थ भर देते हैं।
(ब) को कम कर प्लेटों का क्षेत्रफल बढ़ा देते हैं।
(स) को बढ़ाकर प्लेटों का क्षेत्रफल घटा देते हैं।
(द) भी बढ़ा देते हैं तथा क्षेत्रफल भी बढ़ा देते हैं।
उत्तर:
(स) को बढ़ाकर प्लेटों का क्षेत्रफल घटा देते हैं।

42. एक आवेशित संधारित्र की दोनों प्लेटों को एक तार से जोड़ दिया जाये तो-
(अ) विभव अनन्त हो जायेगा।
(ब) आवेश अनन्त हो जायेगा।
(स) संधारित्र निरावेशित हो जायेगा।
(द) आवेश पूर्णमान का दुगुना हो जायेगा।
उत्तर:
(स) संधारित्र निरावेशित हो जायेगा।

43. ( 8 μF – 250V) अंकित अनेक संधारित्र दिये गये हैं। एक (16 μF – 1000V) की तुल्यधारिता प्राप्त करने के लिए आवश्यक संधारित्रों की न्यूनतम संख्या होगी-
(अ) 4
(ब) 16
(स) 32
(द) 64
उत्तर:
(स) 32

44. एक समान्तर पट्ट संधारित्र की प्लेटों के बीच समरूप क्षेत्र E वोल्ट/मीटर है। यदि प्लेटों के बीच की दूरी d (मी) तथा प्रत्येक प्लेट का क्षेत्रफल A (मी²) है तो उसमें संचित कल ऊर्जा है-
(अ) \(c\frac{1}{2} \epsilon_0 E^2 \mathrm{Ad}\)
(ब) \(\frac{\mathrm{E}^2 \mathrm{Ad}}{\epsilon_0} \)
(स) \(\frac{1}{2} \epsilon_0 E^2 \)
(द) ∈₀AEd
उत्तर:
(अ) \(c\frac{1}{2} \epsilon_0 E^2 \mathrm{Ad}\)

45. एक C धारिता का तथा दूसरा \(\frac{C}{2}\) धारिता का संधारित्र एक V बोल्ट की बैटरी से चित्र के अनुसार जोड़े गये हैं। दोनों संधारित्रों को पूर्णतया आवेशित करने में किया गया कार्य है-
(अ) \(\frac{3}{4}\)CV²
(ब) \(\frac{1}{2}\)CV²
(स) \(\frac{1}{4}\)CV²
(द) 2CV^-2

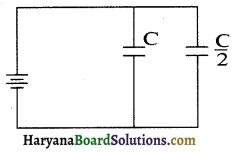
उत्तर:
(अ) \(\frac{3}{4}\)CV²

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
किसी बिन्दु पर विभव को परिभाषित कीजिए ।
उत्तर:
वैद्युत क्षेत्र में किसी बिन्दु पर विभव कार्य की वह मात्रा है जो एकांक धन आवेश को अनन्त से उस बिन्दु तक बिना त्वरण के लाने में करना पड़ता है।

प्रश्न 2.
विभवान्तर को परिभाषित करते हुए इसका मात्रक लिखिए।
उत्तर:
विद्युत क्षेत्र में दो बिन्दुओं के बीच विभवान्तर एक एकांक धन परीक्षण आवेश को एक बिन्दु से दूसरे बिन्दु तक क्षेत्र के विपरीत ले जाने में किए गए कार्य से इसकी परिभाषा देते हैं। S. I. पद्धति में इसका मात्रक वोल्ट (V) या J/C

प्रश्न 3.
किसी क्षेत्र में वैद्युत विभव V नियत है। वहाँ पर आप वैद्युत क्षेत्र E के सम्बन्ध में क्या कह सकते हैं?
उत्तर:
हमारा कहना यह होगा कि उस क्षेत्र में वैद्युत क्षेत्र E शून्य होगा।

प्रश्न 4.
दो बिन्दुओं के बीच विभवान्तर 20 वोल्ट है। एक बिन्दु से दूसरे बिन्दु तक 4 × 10_-4 कूलॉम ले जाने में कितना कार्य करना होगा?
उत्तर:
कार्य (W) = आवेश (q) x विभवान्तर (V)
= 4 × 10^-4 × 20 = 8 × 10^-3 जूल

प्रश्न 5.
क्या निर्वात (vacuum) में किसी बिन्दु पर वैद्युत विभव शून्य हो सकता है, जबकि उस बिन्दु पर वैद्युत क्षेत्र शून्य नहीं है?
उत्तर:
हाँ, (i) दो समान परिमाण तथा विपरीत प्रकृति के आवेशों को मिलाने वाली रेखा के मध्य बिन्दु पर वैद्युत विभव शून्य होता है, वैद्युत क्षेत्र नहीं ।
(ii) वैद्युत द्विध्रुव की निरक्षीय स्थिति में वैद्युत विभव शून्य होता है, वैद्युत क्षेत्र नहीं।

प्रश्न 6.
क्या किसी बिन्दु पर वैद्युत क्षेत्र शून्य हो सकता है, जबकि उसी बिन्दु पर वैद्युत विभव शून्य न हो। उदाहरण दीजिए।
उत्तर:
हाँ, (i) दो समान परिमाण तथा समान प्रकृति के आदेशों को मिलाने वाली रेखा के मध्य बिन्दु पर वैद्युत क्षेत्र शून्य होता है, वैद्युत विभव नहीं।
(ii) आवेशित गोलीय कोश के अन्दर वैद्युत क्षेत्र शून्य होता है, वैद्युत विभव नहीं।

प्रश्न 7.
उस भौतिक राशि का नाम बताइए जिसका मात्रक जूल / कूलॉम है क्या यह सदिश राशि है अथवा अदिश?
उत्तर:
वैद्युत विभव अथवा वैद्युत विभवान्तर अदिश ।

प्रश्न 8.
धातु के 5 cm त्रिज्या के एक खोखले गोले को इतना आवेशित किया गया है कि उसके पृष्ठ का विभव 10V हो जाता है। इस गोले के केन्द्र पर विभव कितना होगा?
उत्तर:
खोखले गोले के केन्द्र व पृष्ठ पर विद्युत विभव समान होता है। अतः गोले के केन्द्र पर विभव V = 10 वोल्ट होगा।

प्रश्न 9.
समविभव पृष्ठ किसे कहते हैं? बिन्दु धनात्मक आवेश के कारण समविभव पृष्ठ का चित्र बनाइए ।
उत्तर:
ऐसा पृष्ठ जिसके प्रत्येक बिन्दु पर विभव समान होता है, समविभव पृष्ठ कहलाता है।

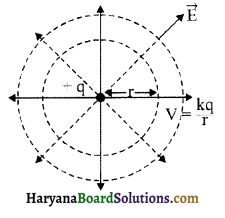
प्रश्न 10.
उस क्षेत्र के तदनुरूप तीन समविभव पृष्ठ खींचिये जिसके परिमाण में एकसमान वृद्धि होती है, परन्तु z-दिशा के अनुदिश नियत रहता है। ये पृष्ठ उन पृष्ठों से किस प्रकार भिन्न हैं जो किसी नियत विद्युत क्षेत्र के 2-दिशा के अनुदिश हैं?
उत्तर:

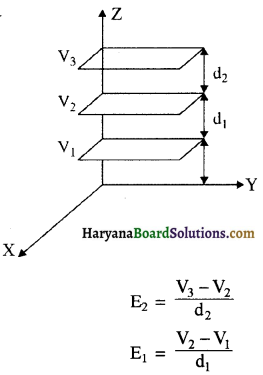
यदि E एकसमान हो तो d₂ = d₁
एकसमान क्षेत्र के लिए प्रत्येक तल पर विभव समान होगा।

प्रश्न 11.
एक समविभव पृष्ठ एक-दूसरे से 5 सेमी. दूरी पर स्थित बिन्दुओं के बीच 500 HC आवेश को ले जाने में कितना कार्य करना पड़ेगा?
उत्तर:
समविभव पृष्ठ के किन्हीं भी दो बिन्दुओं के बीच विभवान्तर ∆V = शून्य
अतः कार्य W = आवेश q × विभवान्तर (∆V)
= 100 µC × 0 = शून्य
अर्थात् कोई कार्य नहीं करना पड़ेगा।

प्रश्न 12.
वैद्युत विभव के मात्रक की परिभाषा दीजिए।
उत्तर:
वैद्युत विभव का मात्रक वोल्ट होता है, जिसको निम्न प्रकार परिभाषित किया जाता है-“यदि एक कूलॉम परीक्षण धनावेश को अनन्त से वैद्युत क्षेत्र के अन्तर्गत किसी बिन्दु तक क्षेत्र की दिशा के विपरीत लाने में एक जूल कार्य करना पड़े तो उस बिन्दु पर वैद्युत विभव का मान एक वोल्ट होगा।”

प्रश्न 13.
निम्नलिखित के कारण समविभव पृष्ठों की आकृति क्या होती है?
(a) बिन्दु आवेश के कारण
(b) एकसमान वैद्युत क्षेत्र के कारण।
उत्तर:
(a) बिन्दु आवेश को केन्द्र मानते हुए खींचे हुए संकेन्द्रीय गोले ।
(b) वैद्युत बल रेखाओं के लम्बवत् परस्पर समान्तर समतल तल ।

प्रश्न 14.
वैद्युत बल रेखाओं के अनुदिश जाने पर वैद्युत विभव घटता है अथवा बढ़ता है?
उत्तर:
विभव घटता है।

प्रश्न 15.
क्या इलेक्ट्रॉन अधिक विभव क्षेत्र में अथवा कम विभव- क्षेत्र में जाने का प्रयत्न करते हैं, क्यों?
उत्तर:
इलेक्ट्रॉन अधिक विभव क्षेत्र में जाने का प्रयत्न करते हैं। क्योंकि ऋणावेशित होते हैं।

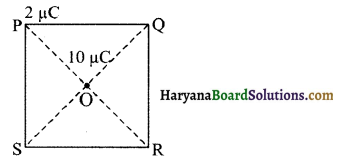
प्रश्न 16.
एक वर्ग PQRS के केन्द्र पर 10 µC आवेश रखा है। इसके कोने P पर रखे 2 µC के बिन्दु आवेश को Q तक ले जाने में किया गया कार्य कितना होगा?
उत्तर:
शून्य, क्योंकि V_p = V_Q एवं P तथा Q की केन्द्र 0 पर स्थित आवेश 10 µC से समान दूरी है।

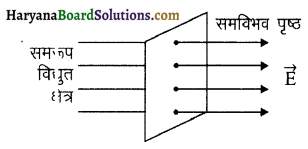
प्रश्न 17.
किसी समरूप विद्युत क्षेत्र में समविभव पृष्ठ खींचिये ।
उत्तर-

प्रश्न 18.
किन्हीं दो समान्तर पृष्ठों पर विभव समान हैं। इनके मध्य की दूरी है। यदि किसी q आवेश को एक पृष्ठ से दूसरे पृष्ठ तक ले जायें तो इस स्थिति में किया गया कार्य कितना होगा?
उत्तर:
किया गया कार्य शून्य होगा क्योंकि दोनों पृष्ठ समान विभव

प्रश्न 19.
दिए गए चित्र में किसी बिन्दु आवेश को x से क्रमशः y तथा z बिन्दुओं तक ले जाने में किया गया कार्य कितना होगा?

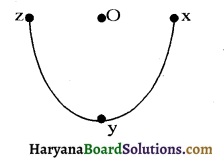
उत्तर:
बिन्दु 2 तथा y एक ही समविभव पृष्ठ पर स्थित हैं। आवेश को x से y तक ले जाने में किया गया कार्य, आवेश को x से 2 तक ले जाने में किए गए कार्य के समान होगा।
इसलिए W_y = W_z

प्रश्न 20.
क्या परीक्षण आवेश की प्रकृति पर धन या ऋण विद्युत विभव निर्भर करता है? समझाइए ।
उत्तर:
नहीं, यह परीक्षण आवेश की प्रकृति पर निर्भर नहीं करता है अपितु केवल स्रोत आवेश की प्रकृति पर निर्भर करता है।

प्रश्न 21.
दो समविभव पृष्ठ एक-दूसरे को नहीं काटते। क्यों?
उत्तर:
यदि दो समविभव पृष्ठ एक-दूसरे को काटते हैं तो इसका अर्थ है कि प्रतिच्छेद बिन्दु पर विद्युत विभव के दो अलग-अलग मान होंगे जो कि सम्भव नहीं है।

प्रश्न 22.
\(\overrightarrow{\mathrm{r}_1} \) तथा \(\overrightarrow{\mathrm{r}_2} \) पर क्रमशः Q₁ तथा Q₂ दो बिन्दु आवेशों के कारण किसी बिन्दु पर जिसका स्थिति सदिश \(\overrightarrow{\mathrm{r}}\) है। वैद्युत विभव (\(\overrightarrow{\mathrm{r}}\)) के लिए व्यंजक लिखिए।
उत्तर:

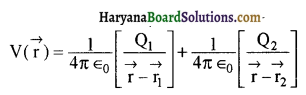
प्रश्न 23.
मध्यवर्ती बिन्दु पर किसी वैद्युत द्विध्रुव के कारण स्थिर वैद्युत विभव क्या होता है?
उत्तर:
शून्य ।

प्रश्न 24.
जब कोई वैद्युत द्विध्रुव किसी वैद्युत क्षेत्र के लम्बवत् रखा जाता है, तो इसकी वैद्युत स्थितिज ऊर्जा क्या होगी ?
उत्तर:
U = -pE cos θ तथा
यहाँ θ = 90°
अतः U = – pE × 0 = 0

प्रश्न 25.
वैद्युत बल रेखा के अनुदिश वैद्युत विभव घटता है अथवा बढ़ता है?
उत्तर:
वैद्युत बल रेखा की दिशा वैद्युत क्षेत्र की दिशा होती है। अतः इस दिशा में वैद्युत विभव घटता है।

प्रश्न 26.
एक परीक्षण आवेश १ को एक वैद्युत द्विध्रुव की मध्यवर्ती अक्ष ( equitorial axis) के अनुदिश एक सेमी ले जाने में कितना कार्य करना होगा?
उत्तर:
चूँकि द्विध्रुव की मध्यवर्ती अक्ष के प्रत्येक बिन्दु पर विभव शून्य होता है, अतः इसके किन्हीं दो बिन्दुओं के बीच विभवान्तर = 0.
अतः कार्य W=q × ∆V = q × 0 = 0

प्रश्न 27.
किसी बाह्य वैद्युत क्षेत्र में आवेश से q r दूरी पर स्थित बिन्दु पर इसकी स्थितिज ऊर्जा की परिभाषा दीजिए।
उत्तर:
किसी आवेश q की बाह्य वैद्युत क्षेत्र में इससे r दूरी पर इसकी स्थितिज ऊर्जा
U = q. V(r)

प्रश्न 28.
चालक तथा अचालक में क्या अन्तर है?
उत्तर:
चालक के सिरों पर वैद्युत विभवान्तर स्थापित करने पर इसमें आवेश का प्रवाह सुगमता से हो जाता है, जबकि ऐसा अचालक में नहीं होता है। चालकों में मुक्त इलेक्ट्रॉनों की संख्या बहुत अधिक होती है जबकि अचालकों में यह संख्या नगण्य होती है।

प्रश्न 29.
परावैद्युत से क्या तात्पर्य है? सिलिकॉन, माइका तथा कार्बन में कौनसा परावैद्युत है?
उत्तर:
परावैद्युत वे अचालक पदार्थ होते हैं जिनमें वैद्युत प्रभाव बिना आवेशों की गति के संचारित हो जाते हैं माइका परावैद्युत पदार्थ है।

प्रश्न 30.
किसी चालक की वैद्युत धारिता से क्या तात्पर्य है?
उत्तर:
किसी चालक द्वारा वैद्युत आवेश ग्रहण करने की क्षमता उसकी वैद्युत धारिता कहलाती है।

प्रश्न 31.
धारिता का मात्रक और इसकी विमा सूत्र लिखो।
उत्तर:
धारिता का SI मात्रक फैरड, विमा सूत्र [M^-1L^-2T⁴+A²]

प्रश्न 32.
धारिता के SI मात्रक की परिभाषा लिखिए।
उत्तर:
यदि किसी चालक को एक कूलॉम आवेश देने से उसके विभव में एक वोल्ट की वृद्धि हो जाये तो उसकी धारिता एक फैरड कहलाती है।

प्रश्न 33.
एक संधारित्र की धनात्मक प्लेट पर + Q व ऋणात्मक प्लेट पर Q आवेश दिया जाता है। संधारित्र पर कुल आवेश क्या होगा? प्लेट पर – Q आवेश दिया जाता है। संधारित्र पर कुल आवेश क्या
उत्तर;
Q, जब हम संधारित्र की एक प्लेट को + Q आवेश देते हैं तब विद्युत प्रेरण के कारण दूसरी प्लेट धरती से जुड़े होने के कारण उस पर Q आवेश आ जाता है। संधारित्र पर कुल आवेश शून्य है।

प्रश्न 34.
समान्तर प्लेट संधारित्र की प्लेटों के मध्य के स्थान को आंशिक रूप से परावैद्युत पदार्थ भरने पर धारिता का मान परावैद्युत पदार्थ की स्थिति पर किस प्रकार निर्भर करता है ?
उत्तर:
निर्भर नहीं करता।

प्रश्न 35.
एक समान्तर प्लेट संधारित्र की एक प्लेट का क्षेत्रफल आधा कर दिया जाये तो क्या युक्ति संधारित्र का कार्य करेगी ?
उत्तर;
नहीं, संधारित्र की एक प्लेट का क्षेत्रफल आधा करने से संधारित्र की धारिता आधी रह जायेगी इसलिये वह युक्ति कार्य नहीं करेगी।

प्रश्न 36.
धारिता C के संधारित्र को V विभवान्तर से आवेशित किया जाता है। संधारित्र के चारों ओर पृष्ठ से गुजरने वाले विद्युत फलक्स का मान क्या होगा ?
उत्तर:
शून्य, चूँकि विद्युत क्षेत्र संधारित्र की दो प्लेटों के मध्य में ही होता है।

प्रश्न 37.
एक फैरड विद्युत धारिता वाले चालक गोले की त्रिज्या क्या होगी ?
उत्तर:
दिया है-
C= 1 फैरड
R = ?
∵ C = 4π∈₀R
∴ R = \(\frac{C}{4 \pi \epsilon_0}\) = \(\frac{1}{4 \pi \epsilon_0}\) × C
R = 9 × 10⁹ × 1 = 9 × 10⁹ मीटर

प्रश्न 38.
तीन संधारित्र जिनके प्रत्येक की धारिता 6 μF है, के संयोजनों से प्राप्त अधिकतम व न्यूनतम धारिताओं का मान क्या होगा?
उत्तर:
अधिकतम धारिता = 6 μF + 6 μF + 6 μF
= 18 μF
न्यूनतम धारिता \(\frac{1}{\mathrm{C}}\) = \(\frac{1}{\mathrm{6}}\) + \(\frac{1}{\mathrm{6}}\) + \(\frac{1}{\mathrm{6}}\) = \(\frac{3}{\mathrm{6}}\) = \(\frac{1}{\mathrm{2}}\)
C = 2 μF

प्रश्न 39.
संधारित्रों का उपयोग कम्प्यूटरों में किस उद्देश्य के लिये किया जाता है?
उत्तर:
मेमोरी संग्रहित करने के लिये ।

प्रश्न 40.
समान्तर प्लेट संधारित्र की धारिता का सूत्र लिखिये । धारिता पर प्लेटों के क्षेत्रफल का क्या प्रभाव पड़ता है?
उत्तर:
समान्तर प्लेट संधारित्र की धारिता C = \(\frac{\epsilon_0 A}{d}\)
समीकरण से स्पष्ट है कि समान्तर संधारित्र की धारिता प्लेटों के क्षेत्रफल के समानुपाती और उनके मध्य की दूरी के प्रतिलोमानुपाती होती है। प्लेटों का क्षेत्रफल A बढ़ाकर धारिता बढ़ाई जा सकती है।

प्रश्न 41.
समान धारिता C की दो संधारित्रों को श्रेणीक्रम में जोड़ा गया है। संयोजन की धारिता क्या होगी?
उत्तर:
श्रेणीक्रम में संयोजन की धारिता \(\frac{1}{\mathrm{C}}\) = \(\frac{1}{C_1}+\frac{1}{C_2}\)
संयोजन की धारिता = \(\frac{C}{2}\) होगी।

प्रश्न 42.
संधारित्र की धारिता पर परावैद्युत माध्यम का क्या प्रभाव पड़ता है?
उत्तर:
परावैद्युत माध्यम की उपस्थिति में धारिता के मान में वृद्धि हो जाती है। लेकिन यह वृद्धि इस बात पर निर्भर करती है कि प्लेटों के मध्य का भाग परावैद्युत पदार्थ से पूर्णतः आंशिक या विभिन्न परतों के रूप में कैसे-कैसे भरा हुआ है।

प्रश्न 43.
3 μF व 5 μF धारिता के दो संधारित्रों के समान्तर संयोजन को Q आवेश दिया जाता है। यदि 3 μF पर आवेश Q₁ तथा 5 μF पर Q₂ हो तो \( \frac{\mathrm{Q}_1}{\mathrm{Q}_2}\) का मान क्या होगा ?
उत्तर:
\( \frac{\mathrm{Q}_1}{\mathrm{Q}_2}=\frac{\mathrm{C}_1}{\mathrm{C}_2}=\frac{3}{5}\)

प्रश्न 44.
एक संधारित्र की प्लेटों के बीच रखे पदार्थ का परावैद्युतांक 5 है और इसकी धारिता C है। यदि इसको परावैद्युतांक 20 वाले पदार्थ से प्रतिस्थापित कर दिया जाये तो संधारित्र की नई धारिता क्या होगी ?
उत्तर:
संधारित्र की नई धारिता का मान पहले वाली धारिता का चार गुना होगा।

प्रश्न 45.
नीचे दिखाये गये परिपथ में A, बिन्दु पर विभव 100 वोल्ट है। बिन्दु B पर विभव होगा-

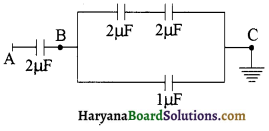
उत्तर:
बिन्दु B पर विभव 50 वोल्ट होगा।

प्रश्न 46.
तीन संधारित्र, परिपथ चित्र में दिखाये अनुसार व्यवस्थित हैं। बिन्दु A व B के मध्य कुल धारिता 3 μF है, तो X संधारित्र की धारिता का मान होगा-
उत्तर:

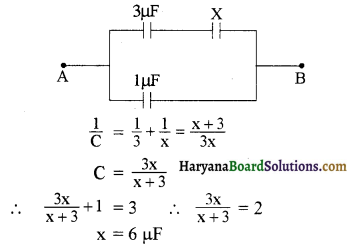
प्रश्न 47.
दिये गये परिपथ चित्र में A व B के बीच तुल्यधारिता ज्ञात कीजिए।

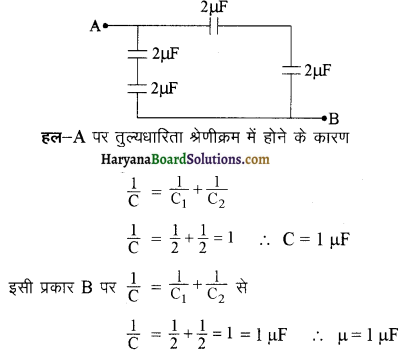
इसलिये A तथा B के बीच में तुल्यधारिता = 1+1=2pF उत्तर

प्रश्न 48.
एक आवेशित संधारित्र की प्लेटों को एक-दूसरे से दूर हटाने से प्लेटों के बीच विभवान्तर पर क्या प्रभाव पड़ेगा?
उत्तर:
प्लेटों के बीच में विभवान्तर बढ़ेगा।

प्रश्न 49.
क्या समान आयतन के दो चालकों के बीच विभवान्तर हो सकता है, जबकि दोनों पर समान धनावेश है ?
उत्तर:
हाँ, क्योंकि समान आयतन के दो चालकों का आकार भिन्न हो सकता है, जिसके कारण धारिता भिन्न होने के कारण विभव भिन्न-भिन्न होंगे अर्थात् उनके बीच विभवान्तर होगा ।

प्रश्न 50.
एक ग्राफ खींचिये जो धारिता के संधारित्र को दिये गये आवेश Q तथा उसके विभवान्तर V के बीच सम्बन्ध बताता हो।
उत्तर:

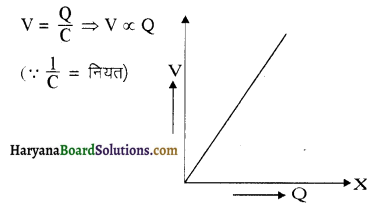
प्रश्न 51.
समविभव पृष्ठ को परिभाषित कीजिए।
उत्तर:
ऐसा पृष्ठ जिसके प्रत्येक बिन्दु पर विभव समान होता है, समविभव पृष्ठ कहलाता है। समविभव पृष्ठ के किन्हीं दो बिन्दुओं के बीच विभवान्तर का मान शून्य होता है अतः समविभव पृष्ठ के किसी एक बिन्दु से दूसरे बिन्दु तक किसी आवेश को ले जाने में किया गया कार्य शून्य के बराबर होता है किन्तु किया गया कार्य शून्य तभी होता है जब आवेश को विद्युत क्षेत्र के लम्बवत् दिशा में ले जाया जाता है। अतः समविभव पृष्ठ विद्युत क्षेत्र के प्रत्येक बिन्दु पर लम्बवत् होता है।

प्रश्न 52.
4 × 10^-9C आवेश के कारण इससे 9 × 10^-2 मी. दूरी पर स्थित किसी बिन्दु पर विभव परिकलित कीजिए ।
हल- दिया है-
q = 4 × 10^-9 C
r = 9 × 10^-2 मी.
हम जानते हैं

प्रश्न 53.
4 μF धारिता का मान कितना होगा यदि समांतर प्लेट संधारित्र की प्लेटों के मध्य 2 परावैद्युतांक का परावैद्युत पूर्णतः भर दिया जाए?
हल – जब प्लेटों के बीच सम्पूर्ण स्थान में ∈_r परावैद्युतांक का माध्यम भरा हुआ हो, तब C = C₀∈_r होता है।
इसलिये C = 4 × 2 = 8 μF

प्रश्न 54.
किसी माध्यम के परावैद्युतांक की परिभाषा लिखिये। इसका एस.आई. (S.I.) मात्रक क्या है ?
उत्तर:
हम जानते हैं
C = C₀∈_r
या ∈_r = \(\frac{C}{C_0}\)
अतः किसी माध्यम के परावैद्युतांक का मान, परावैद्युत पदार्थ से पूर्णतया भरी समांतर प्लेट संधारित्र की धारिता का मान C, हवा या निर्वात धारिता C के अनुपात के बराबर होता है। इसका कोई भी मात्रक नहीं होता है।

लघुत्तरात्मक प्रश्न

प्रश्न 1.
एक बिन्दु आवेश ‘q’ बिन्दु 0 पर चित्र में दिखाये अनुसार रखा है। क्या (V_A – V_B) धनात्मक, ऋणात्मक अथवा शून्य होगा यदि q (i) धनात्मक है (ii) ऋणात्मक ‘

होगी इसलिए V_A – V_B का चिन्ह q के चिन्ह पर निर्भर करेगा ।
(∵ 4π∈₀ = नियतांक)
अतः (i) q के धनात्मक होने पर (V_A – V_B) धनात्मक होगा।
(ii) q के ऋणात्मक होने पर (_A – V_B) ऋणात्मक होगा।

प्रश्न 2.
एक लघु वैद्युत द्विध्रुव के कारण अत्यधिक दूरी पर उत्पन्न वैद्युत विभव की दूरी पर निर्भरता बताइए, जबकि प्रेक्षण बिन्दु
(i) अक्षीय स्थिति में हो, तथा
(ii) निरक्षीय स्थिति में हो।
उत्तर:
(i) अक्षीय स्थिति में विभव (V) = \( \frac{1}{4 \pi \epsilon_0}\left(\frac{p}{r^2}\right)\)
अतः स्पष्ट है V ∝ \(\frac{1}{r^2}\)
(ii) निरक्षीय स्थिति में V = 0, अतः यह दूरी पर निर्भर नहीं करता है। अर्थात् इस स्थिति में प्रत्येक बिन्दु पर वैद्युत विभव शून्य होता है।

प्रश्न 3.
समविभव पृष्ठ की परिभाषा दीजिए। इसकी विशेषताएँ लिखिए ।
उत्तर:
परिभाषा – किसी वैद्युत क्षेत्र में वह पृष्ठ जिसके प्रत्येक बिन्दु का विभव समान होता है, समविभव पृष्ठ कहलाता है।
विशेषताएँ – (i) इसके किन्हीं भी दो बिन्दुओं के बीच विभवान्तर शून्य होता है।
(ii) इसके किन्हीं भी दो बिन्दुओं के बीच किसी आवेश को ले जाने में कोई कार्य नहीं करना पड़ता।
(iii) वैद्युत क्षेत्र सदैव समविभव पृष्ठ के लम्बवत् रहता है।

प्रश्न 4.
वैद्युत विभव तथा वैद्युत स्थितिज ऊर्जा में भेद स्पष्ट कीजिए तथा इनके बीच सम्बन्ध बताइए ।
उत्तर:
वैद्युत विभव एकांक धन आवेश को बिना त्वरण के अनन्त से लाने में किया गया कार्य है जबकि वैद्युत स्थितिज ऊर्जा दिये गये आवेशों को अनन्त से उनकी स्थिति तक लाने में किया गया कार्य होती है।
वैद्युत विभव V = \(\frac{1}{4 \pi \epsilon_0}\left(\frac{\mathrm{q}_1}{\mathrm{r}}\right)\) तथा U = \(\frac{1}{4 \pi \epsilon_0}\left(\frac{q_1 q_2}{r}\right)\)
जहाँ प्रतीकों के सामान्य अर्थ हैं। उपर्युक्त व्यंजकों से स्पष्ट है कि
U = \(\frac{1}{4 \pi \epsilon_0}\left(\frac{q_1}{\mathrm{r}}\right)\) . q₂
U = q₂ . V
अतः q₁ तथा q₂आवेशों (जो परस्पर 1 दूरी पर स्थित ) बने निकाय की स्थितिज ऊर्जा
U = आवेश q₂ x
(आवेश q₁ के कारण q₂ की स्थिति में विभव)

प्रश्न 5.
किसी बिन्दु आवेश से दूरी में परिवर्तन के संगत होने वाले विभव परिवर्तन दर्शाने वाला ग्राफ बनाइए चित्र में प्रदर्शित आवेश निकाय के लिए सिद्ध कीजिए कि बिन्दुओं A व B के मध्य विभवान्तर

प्रश्न 6.
इस सत्य की भौतिक व्याख्या कीजिए कि धन आवेश युग्म की स्थितिज ऊर्जा धनात्मक होती है।
उत्तर:
धन आवेश युग्म के दो आवेश आपस में प्रतिकर्षित करेंगे और त्वरित गति से एक-दूसरे से दूर हो जायेंगे जब तक उनके बीच की दूरी अनन्त नहीं हो जाये। उन आवेशों में गति उनके अन्दर स्थितिज ऊर्जा के कारण ही सम्भव है। इसलिए धन आवेश युग्म की स्थितिज ऊर्जा धनात्मक होती है।

प्रश्न 7.
ध्रुवण को परिभाषित कीजिए।
उत्तर:
आयतित विद्युत क्षेत्र में परावैद्युत में परमाणुओं को खींचकर आवेशों को पृथक करने के प्रक्रम को ध्रुवण कहते हैं। परमाणुओं का खिंचाव तब तक चलता है जब तक कि आवेशों पर विद्युत क्षेत्र द्वारा आयोजित बल प्रत्यानयन बल के तुल्य नहीं हो जाता। इस तनन के कारण नाभिक का धनात्मक गुरुत्व केन्द्र ऋणात्मक गुरुत्व केन्द्र, जो इलेक्ट्रॉनों के कारण बनता है, एक-दूसरे से अलग हो जाते हैं और इस प्रकार परमाणु द्विध्रुव आघूर्ण प्राप्त कर लेते हैं। अर्थात् किसी पदार्थ का प्रति एकांक आयतन द्विध्रुव आघूर्ण उसका ध्रुवण कहलाता है तथा इसे \(\vec{p}\) द्वारा निर्दिष्ट किया जाता है। रैखिक समदैशिक परावैद्युतों के लिए
\(\overrightarrow{\mathrm{p}}=\chi_0 \mathrm{E}\)
यहाँ X_o परावैद्युतका स्थिर अभिलक्षण है जिसे परावैद्युत माध्यम की वैद्युत प्रवृत्ति कहते हैं।

प्रश्न 8.
एक सीधी रेखा में समान दूरियों पर तीन आवेश q, Q तथा – q स्थित हैं। यदि तीनों आवेशों के निकाय की कुल स्थितिज ऊर्जा शून्य हो तो Q : q अनुपात का मान कितना होगा?
उत्तर:
निकाय की कुल स्थितिज ऊर्जा का मान होगा-

प्रश्न 9.
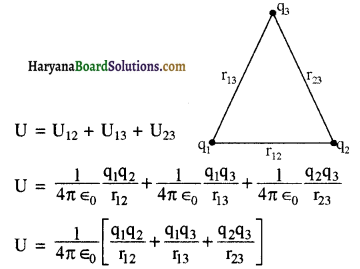
तीन बिन्दु आवेशों से निर्मित किसी तंत्र की स्थितिज ऊर्जा ज्ञात कीजिए।
उत्तर:
तीन आवेशों q₁, q₂ तथा q₃ से निर्मित तंत्र को सामने चित्र में प्रदर्शित किया गया है। इस तंत्र की कुल स्थितिज ऊर्जा

प्रश्न 10.
एक गोलाकार चालक कोश की त्रिज्या R है व उस पर आवेश Q है। गोले के केन्द्र से (2R) दूरी पर विभव की तुलना \(\frac{\mathbf{R}}{\mathbf{2}}\) दूरी पर विभव से कीजिए।
उत्तर:
हम जानते हैं कि बाह्य बिन्दुओं के लिए आवेशित चालक कोश इस तरह से व्यवहार करता है जैसे उसका आवेश उसके केन्द्र पर स्थित हो अतः केन्द्र से (2R) दूरी पर विभव का मान माना V₁ है।
अतः V₁ = \(\frac{1}{4 \pi \epsilon_0} \frac{Q}{2 R}\) ………..(1)
गोलीय कोश के अन्दर विभव नियत होता है तथा वह उसके पृष्ठ पर विभव के तुल्य होता है। अतः केन्द्र से R/2 दूरी पर विभव का मान माना (V₂) है।
V₂ = \(\frac{1}{4 \pi \epsilon_0} \frac{Q}{R}\) …………(2)
अतः \(\frac{V_1}{V_2}\) = \(\frac{1}{2}\)

प्रश्न 11.
किसी द्विध्रुव की विद्युत क्षेत्र में स्थितिज ऊर्जा के लिए सूत्र लिखिए तथा इनके न्यूनतम व अधिकतम मान ज्ञात कीजिए।
हल-विद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}\) में क्षेत्र के लम्बव्त् द्विध्रुव की स्थिति θ = 90° को निर्देश स्थिति मानते हुए अन्य स्थिति पर स्थितिज ऊर्जा का मान
U = \(-\overrightarrow{\mathrm{P}} \cdot \overrightarrow{\mathrm{E}}\) = – PE cos θ
θ = 0, अर्थात् क्षेत्र के समान्तर स्थिति में
U = U_min = – PE
θ = π, अर्थात् क्षेत्र के विरुद्ध दिशा में
U = U_max = + PE
∵ cos π = -1

प्रश्न 12.
अधुवी व ध्रुवी परमाणुओं या अणुओं में अन्तर उदाहरण देकर समझाइए ।
उत्तर:
अधुवी परमाणुओं या अणुओं में ऋण व धन आवेशों के वितरण केन्द्र सम्पाती होते हैं, जिससे द्विध्रुव आघूर्ण शून्य रहता है। ध्रुवी अणुओं में इन आवेशों के वितरण केन्द्रों के मध्य अन्तराल होता है और अणु का स्थायी द्विध्रुव आघूर्ण होता है।
N₂, CH₄, OH₂, O₂ आदि अध्रुवी हैं जबकि H₂O, NH₃ HCI आदि ध्रुवी अणु हैं।

प्रश्न 13.
धुवी तथा अधुवी परावैद्युत में अन्तर लिखिए।
उत्तर:
ध्रुवी तथा अधुवी परावैद्युत में अन्तर

ध्रुवी परावैद्युत	अधुवी परावैद्युत
1. इनके अणु बाह्य वैद्युत क्षेत्र की अनुपस्थिति में भी नैट विद्युत द्विध्रुव आघूर्ण रखते हैं।	इनके अणुओं में कोई स्थायी वैद्युत द्विध्रुव आघूर्ण नहीं होता। बाह्य वैद्युत क्षेत्र में रखे जाने पर ध्रुवण अवस्था में यह आघूर्ण उत्पन्न होता है।
2. इनके अणुओं की रचना असममित होती है। उदाहरणार्थ- NH3	इनके अणुओं की रचना सममित होती है। उदाहरणार्थ- O2

प्रश्न 14.
संधारित्र का सिद्धान्त लिखिए।
उत्तर:
आवेशित चालक का विभव उसके समीप एक अन्य भू- सम्पर्कित चालक को रखकर कम किया जा सकता है इस प्रकार चालक की आवेश संग्रहित करने की क्षमता जिसे हम धारिता कहते हैं, बढ़ जाती है। ऐसे समायोजन को संधारित्र कहते हैं।

प्रश्न 15.
संधारित्र की धारिता पर परावैद्युत माध्यम का क्या प्रभाव पड़ता है?
उत्तर:
परावैद्युत माध्यम की उपस्थिति में धारिता के मान में वृद्धि हो जाती है लेकिन यह वृद्धि इस बात पर निर्भर करती है कि प्लेटों के मध्य का भाग परावैद्युत पदार्थ से पूर्णतः आंशिक या विभिन्न परतों के रूप में किस प्रकार भरा हुआ है।

प्रश्न 16.
क्या एक फैरड धारिता का समान्तर पट्ट संधारित्र आपकी आलमारी में रखना सम्भव है?
हल-चूँकि चालक की धारिता C = 4π∈₀R होती है, इसलिए इसकी त्रिज्या का मान
R = \(\frac{C}{4 \pi \epsilon_0}\) = 9 × 10⁹ मीटर/फैरड × 1 फैरड
= 9 × 10⁹ मीटर = 9 × 10⁶ किमी.
अतः यह त्रिज्या बहुत बड़ी है। अर्थात् 1 फैरड धारिता का गोलाकार चालक बनाना सम्भव नहीं है, जिसको अलमारी में रखना सम्भव नहीं है।

प्रश्न 17.
क्या 1 सेमी. त्रिज्या का धात्वीय गोला 1 कूलॉम आवेश ग्रहण कर सकता है?
हल – R = 1 सेमी = 1 × 10^-2 मीटर त्रिज्या के गोले को Q = एक कूलॉम आवेश देने पर इसकी सतह पर वैद्युत क्षेत्र की तीव्रता
E = \( \frac{1}{4 \pi \epsilon_0}\left(\frac{Q}{R}\right)=9 \times 10^9 \times\left(\frac{1}{10^{-2}}\right)\)
= 9 × 10¹¹ न्यूटन/कूलॉम
= 9 × 10¹¹ वोल्ट/मीटर
यह चालक की वैद्युत सामर्थ्य होगी, लेकिन वायु की परावैद्युत सामर्थ्य 3 × 10₆ वोल्ट / मीटर होती है इसलिए चालक के चारों ओर की निकटतम वायु आयनीकृत हो जायेगी, जिससे कि गोले के आवेश का वायु में क्षरण होने लगेगा अतः कहा जा सकता है कि एक सेमी. त्रिज्या का गोला एक कूलॉम आवेश ग्रहण नहीं कर सकता है।

प्रश्न 18.
A और B दो समान त्रिज्या के चालक गोले हैं, जिसमें A गोला ठोस है और B खोखला है। दोनों को समान विभव तक आवेशित किया जाता है। दोनों गोलों पर आवेशों में क्या सम्बन्ध होगा?
उत्तर:
गोला चाहे ठोस हो अथवा खोखला हो, आवेश उसके बाहरी पृष्ठ पर रहता है। चूँकि गोलाकार चालक की धारिता उसकी त्रिज्या के अनुक्रमानुपाती होती है। यहाँ पर दोनों गोलों की त्रिज्या समान है। अतः दोनों की धारितायें भी समान होंगी। अतः C_A = C_B = C माना दोनों गोलों पर समान विभव (माना V तक) आवेशित किया गया है।
अर्थात् V_A = V_B = V, अतः इनका आवेश क्रमश: Q_A= C_AV_A = CV, Q_B = C_BV_B = CV
∴ Q_A : Q_B = 1 : 1 अर्थात् दोनों पर आवेश समान होगा।

प्रश्न 19.
समान्तर पट्ट संधारित्र की प्लेटों के बीच एक धातु की पन्नी (foil) रखने पर उसकी धारिता पर क्या प्रभाव पड़ेगा?
उत्तर:
संधारित्र की प्लेटों के बीच वायु होने पर धारिता C₀ = \( \frac{\epsilon_0 A}{\mathrm{~d}}\)
इसकी प्लेटों के बीच धातु की पन्नी रखने पर (चित्र) यह संधारित्र दो समान्तर पट्ट संधारित्र के श्रेणी संयोजन के तुल्य होगा, जिनमें प्रत्येक प्लेट का क्षेत्रफल A तथा प्लेटों के बीच की दूरी = \(\frac{\mathrm{d}}{2}\)

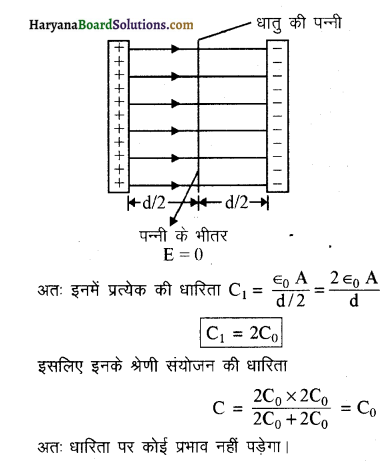
प्रश्न 20.
संधारित्रों के समान्तर संयोजन व श्रेणी संयोजन में अन्तर लिखिये।
उत्तर:
(1) संधारित्रों का ऐसा संयोजन जिसमें प्रत्येक संधारित्र पर विभवान्तर का मान एकसमान हो, उसे समान्तर संयोजन कहते हैं। संधारित्रों का ऐसा संयोजन, जिसमें प्रत्येक संधारित्र पर आवेश का परिमाण एकसमान रहता है उसे श्रेणी संयोजन कहते हैं।

(2) संधारित्रों को समान्तर क्रम में संयोजित करने पर संयोजन की तुल्यधारिता, प्रत्येक संधारित्र की धारिता के योग के बराबर होती है। श्रेणी संयोजन में परिपथ की तुल्यधारिता का व्युत्क्रम, इस संयोजन में प्रयुक्त प्रत्येक संधारित्र की
धारिता के व्युत्क्रम के योग के बराबर होता है। श्रेणी संयोजन में प्राप्त तुल्यधारिता का मान किसी भी धारिता के मान से भी कम होता है।

प्रश्न 21.
एक गोलीय चालक पर आवेश की मात्रा तीन गुनी करने पर उसकी धारिता में कितने प्रतिशत वृद्धि होगी ?
उत्तर:
चालक पर आवेश में परिवर्तन करने पर उसके विभव में उसी अनुपात में परिवर्तन हो जाता है अतः आवेश व विभव वृद्धि का अनुपात स्थिर रहता है। इसलिए चालक की धारिता के मान में कोई परिवर्तन नहीं होगा।

प्रश्न 22.
एक समान्तर प्लेट संधारित्र की प्लेटों के बीच दो परावैद्युत गुटके (जिनके परावैद्युतांक क्रमश: K₁ तथा K₂ हैं) चित्र में दर्शाये अनुसार भरे हुए हैं। संधारित्र की धारिता क्या होगी?

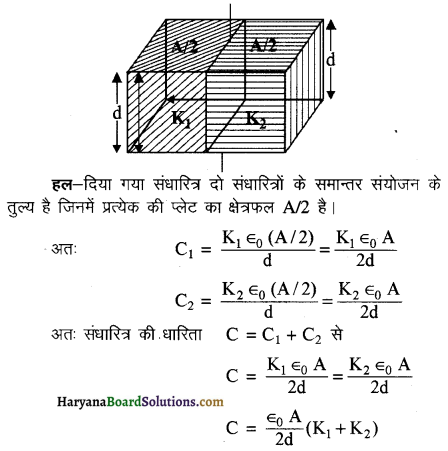
प्रश्न 23.
एक समान्तर पट्ट संधारित्र एक दिष्टधारा स्रोत से v विभवान्तर तक आवेशित किया गया है, जबकि प्लेटों के बीच वायु है। संधारित्र को बैटरी से अलग किये बिना वायु के स्थान पर K परावैद्युतांक का परावैद्युत माध्यम भर दिया गया है। कारण सहित बताइए कि निम्नलिखित में से क्या परिवर्तन होगा? उत्तरों का स्पष्टीकरण भी दो ।
(i) विभवान्तर
(ii) प्लेटों के बीच वैद्युत क्षेत्र
(iii) धारिता
(iv) आवेश
(v) ऊर्जा
उत्तर:
(i) चूँकि यहाँ पर संधारित्र को बैटरी से जोड़ा गया है, अतः वैद्युत विभवान्तर V अपरिवर्तित रहेगा।
(ii) चूँकि विभवान्तर और प्लेटों के मध्य की दूरी दोनों अपरिवर्तित हैं, अतः वैद्युत क्षेत्र \(E=\frac{V}{d} \) अपरिवर्तित रहेगा।
(iii) धारिता बढ़ जायेगी : ∵ C = KC₀
(iv) चूँकि V नियत है और धारिता K गुनी हो जाती है, अतः आवेश Q भी K गुना हो जायेगा।
(v) प्रारम्भिक ऊर्जा \(\mathrm{U}_0=\frac{1}{2} \mathrm{C}_0 \mathrm{~V}_0^2\) और बाद में ऊर्जा U = \(\frac{1}{2} \mathrm{KC}_0 \mathrm{~V}_0^2=\mathrm{KU}_0\) अर्थात् ऊर्जा भी बढ़कर K गुनी हो जायेगी।

प्रश्न 24.
C धारिता के n संधारित्रों को श्रेणीक्रम में संयोजित करने पर तुल्यधारिता C_s तथा समान्तर क्रम में संयोजित करने पर तुल्यधारिता C_p है। सिद्ध कीजिए कि
उत्तर:

प्रश्न 25.
आवेशों के निकाय के कारण विद्युत विभव के मान की गणना कीजिए ।
उत्तर:
किन्हीं आवेशों q1, q2, q3 , …….. qn के ऐसे निकाय पर विचार करते हैं, जिनके किसी मूल बिन्दु के सापेक्ष स्थिति सदिश क्रमशः
\(\overrightarrow{\mathrm{r}_1}, \overrightarrow{\mathrm{r}_2}, \overrightarrow{\mathrm{r}_3} \ldots \ldots, \overrightarrow{\mathrm{r}_{\mathrm{n}}}\)
बिन्दु P पर आवेश q₁ के कारण विभव
V₁ = \(\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{q}_1}{r_{1 \mathrm{P}}}\)
यहाँ r_1p बिन्दु p तथा आवेश q₁ के बीच की दूरी है।

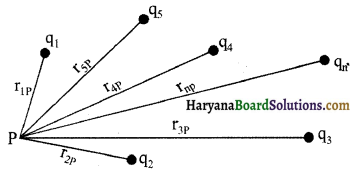
इसी प्रकार बिन्दु P पर आवेश q₂ के कारण विभव V₂ तथा आवेश q₃ के कारण विभव V₃ को भी व्यक्त कर सकते हैं-
V₂ = \(\frac{1}{4 \pi \epsilon_0} \frac{q_2}{r_{2 P}}\)
V₃ = \(\frac{1}{4 \pi \epsilon_0} \frac{q_3}{r_{3 \mathrm{P}}}\)
यहाँ r_2p तथा r_3p बिन्दु p की क्रमशः q₂ तथा q₃ से दूरियाँ हैं। इसी प्रकार हम अन्य आवेशों के कारण बिन्दु p पर विभव व्यक्त कर सकते हैं। अध्यारोपण सिद्धान्त के अनुसार, समस्त आवेश विन्यास के कारण बिन्दु P पर विभव V विन्यास के व्यष्टिगत आवेशों के विभवों के बीजगणितीय योग के बराबर होता है-

प्रश्न 26.
समविभव पृष्ठ किसे कहते हैं? बिन्दु आवेश के लिए समविभव पृष्ठ बनाइए और इनके गुण लिखिए ।
उत्तर:
चित्र में एक बिन्दु आवेश Q, O पर रखा है। O को केन्द्र मानकर r त्रिज्या का गोला बनायें तो गोले की धरातल का प्रत्येक बिन्दु O से समान दूरी पर होगा अतः इस धरातल के प्रत्येक बिन्दु पर विभव का मान \(\frac{\mathrm{KQ}}{\mathrm{r}}\) होगा। इस प्रकार के पृष्ठ को समविभव पृष्ठ कहते हैं।
“विद्युत क्षेत्र में ऐसे पृष्ठ जिनके प्रत्येक बिन्दु पर विद्युत विभव समान होता है, समविभव पृष्ठ कहलाते हैं।” समविभव पृष्ठ के प्रत्येक बिन्दु पर विभव समान होने के कारण किन्हीं भी दो बिन्दुओं के मध्य जो पृष्ठ पर स्थित हैं, विभवान्तर शून्य होता है।

अतः गोले के पृष्ठ पर किसी भी मान के आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में सम्पन्न कार्य शून्य होगा। इस पृष्ठ पर बल रेखायें सदैव पृष्ठ के लम्बवत् होंगी। चित्र में S, S₁, S₂ बिन्दु आवेश Q के लिए समविभव पृष्ठ हैं। ये संकेन्द्रीय गोले हैं।

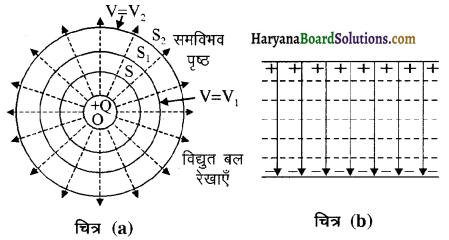
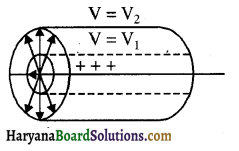
यदि दो समान्तर प्लेटों के मध्य बैटरी जोड़कर निश्चित विभवान्तर स्थापित किया जाये तो प्लेटों के मध्य एकसमान विद्युत क्षेत्र उत्पन्न हो जाता है। इस विद्युत क्षेत्र से समविभव पृष्ठ प्लेटों के समान्तर समतल पृष्ठ होते हैं। जैसा चित्र (b) में दिखाया गया है।
विभवान्तर की परिभाषा के अनुसार एकांक मान के परीक्षण आवेश को एक बिन्दु A से दूसरे बिन्दु B तक विस्थापित करने में किया गया कार्य विभवान्तर के तुल्य होता है।
अर्थात् V_B – V_A = W_AB
यदि बिन्दु A और B एक समविभव तल पर स्थित हैं तो
V_B = V_A ∴ W_AB = 0
अर्थात् समविभव तल पर किसी आवेश को एक बिन्दु से दूसरे तक विस्थापन में कार्य का मान शून्य होता है। रेखीय आवेश के लिए समविभव पृष्ठ बेलनाकार पृष्ठ होता है।

समविभव पृष्ठ के गुण-

1. पृष्ठ के प्रत्येक बिन्दु पर विभव एकसमान होता है।
2. समविभव पृष्ठ पर किसी आवेश को एक बिन्दु से दूसरे बिन्दु तक विस्थापन में किया गया कार्य का मान शून्य होता है।
3. दो समविभव पृष्ठ एक-दूसरे को कभी भी नहीं काटते हैं।
4. विद्युत बल रेखायें पृष्ठ के लम्बवत् होती हैं।
5. किसी भी चाल की सतह हमेशा समविभव पृष्ठ होती है क्योंकि सतह के सभी बिन्दु एक-दूसरे से विद्युत सम्पर्क में होते हैं।

प्रश्न 27.
विद्युत क्षेत्र की तीव्रता \(\overrightarrow{\mathrm{E}}\) तथा वैद्युत विभव में सम्बन्ध स्थापित कीजिए ।
उत्तर:
(Relation between Intensity of Electric field \(\overrightarrow{\mathrm{E}}\) and potential V)
माना q₀ परीक्षण आवेश एक समविभव पृष्ठ से dr दूरी पर स्थित दूसरी समविभव पृष्ठ पर विस्थापित होता है। परीक्षण आवेश पर क्षेत्र द्वारा किया गया कार्य
W = – q₀dV ……………(1)
जहाँ dV = समविभव पृष्ठों के मध्य विभवान्तर है।
इसी कार्य को निम्न समीकरण द्वारा व्यक्त कर सकते हैं-

यहाँ पर आंशिक अवकलन इस बात को दर्शाता है कि समीकरण (3) में V का परिवर्तन उस दिशा में है जिसमें क्षेत्र \(\overrightarrow{\mathrm{E}}\) का घटक स्थित है।

प्रश्न 28.
तीन बिन्दु आवेशों से निर्मित किसी तंत्र की विद्युत स्थितिज ऊर्जा ज्ञात कीजिए।
उत्तर:
अनुच्छेद 2.7 में उदाहरणार्थ देखें ।

प्रश्न 29.
बाह्य क्षेत्र में एकल आवेश की स्थितिज ऊर्जा की गणना कीजिए।
उत्तर:
एकल आवेश की स्थितिज ऊर्जा (Potential energy of a single charge) आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा के लिए हम सूत्र स्थापित कर चुके हैं, जिसमें वैद्युत क्षेत्र के स्रोत अर्थात् आवेशों की स्थितियों को भी ध्यान में रखा गया था। अब यहाँ पर हमें बाहरी विद्युत क्षेत्र में किसी आवेश की वैद्युत स्थितिज ऊर्जा ज्ञात करनी है। यहाँ विद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}\) उत्पन्न करने वाले आवेश अज्ञात हैं।

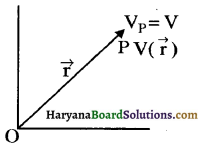
बाहरी विद्युत क्षेत्र ([/latex]\overrightarrow{\mathrm{E}}[/latex]) और किसी बिन्दु पर विद्युत विभव (V) दोनों प्रेक्षण बिन्दु की स्थिति बदलने पर बदल सकते हैं। यदि किसी बिन्दु P पर विद्युत विभव \(V(\vec{r})\) है, जहाँ \(\vec{r}\) बिन्दु P की स्थिति सदिश है, तो विभव की परिभाषा से एकांक आवेश को अनन्त से P बिन्दु तक लाने में किया गया कार्य V जूल होगा। अतः किसी आवेश q को अनन्त से P बिन्दु तक लाने में किया गया कार्य W = q. \(V(\vec{r})\) यही कार्य आवेश में उसकी वैद्युत स्थितिज ऊर्जा के रूप में संचित हो जायेगा।
अतः आवेश q की किसी बाहरी क्षेत्र /latex]\overrightarrow{\mathrm{E}}[/latex] में बिन्दु \(p(\vec{r})\) पर वैद्युत स्थितिज ऊर्जा = q . \(V(\vec{r})\)
यही कार्य आवेश में उसकी वैद्युत स्थितिज ऊर्जा के रूप में संचित हो जायेगा।
अतः आवेश q की किसी बाहरी क्षेत्र \(\overrightarrow{\mathrm{E}}\) में बिन्दु \(\mathrm{P}(\overrightarrow{\mathrm{r}})\) पर वैद्युत स्थितिज ऊर्जा = q. \(\mathrm{q} \cdot \mathrm{V}(\overrightarrow{\mathrm{r}})\)

प्रश्न 30.
किसी बाह्य क्षेत्र में दो आवेशों के निकाय की स्थितिज ऊर्जा की गणना कीजिए। लिखिए।
उत्तर:
किसी बाह्य क्षेत्र में दो आवेशों के निकाय की स्थितिज ऊर्जा (Potential energy of a system of two charges in an external field)
माना किसी बाह्य क्षेत्र \(\overrightarrow{\mathrm{E}}\) में दो आवेश q₁ तथा q₂ क्रमशः \(\overrightarrow{\mathrm{r}_1}\)
तथा \(\overrightarrow{\mathrm{r}_2}\)
अब q₁ आवेश को अनन्त से स्थिति \(\vec{r}_1 \) तक लाने में किया गया कार्य
W₁ = q₁V(\(\vec{r}_1 \)) …………..(1)
यहाँ पर V(\(\vec{r}_1 \)), \(\vec{r}_1 \) दूरी पर स्थित बिन्दु पर विभव का मान है।
जब q₂ आवेश को अनन्त से स्थिति \(\overrightarrow{\mathrm{r}_2}\) तक लाया जाता है तब किया गया कार्य W₂ बाह्य क्षेत्र \( \overrightarrow{\mathrm{E}}\) के विरुद्ध किया गया कार्य +q₁ के कारण क्षेत्र के विरुद्ध किंया गया कार्य

प्रश्न 31.
संधारित्र की धारिता को प्रभावित करने वाले कारक
उत्तर:
संधारित्र की धारिता को प्रभावित करने वाले कारक (Factors effecting the Capacity of a Conductor)
किसी संधारित्र विशेष के लिए उसकी धारिता नियत होती है तथा यह निम्नलिखित कारकों पर निर्भर करती है-

(i) प्लेटों (चालकों) के क्षेत्रफल पर-प्रयोगों के आधार पर यह देखा गया है कि किसी संधारित्र की धारिता उसकी प्लेटों के प्रभावी क्षेत्रफल A के अनुक्रमानुपाती होती है।
अर्थात् C ∝ A

(ii) प्लेटों के बीच की दूरी पर-यदि संधारित्र की प्लेटों के बीच की दूरी d को बढ़ाया जाता है तो संधारित्र की धारिता का मान घट जाता है। चूँकि यह प्लेटों के बीच की दूरी d के व्युत्क्रमानुपाती होती है।

(iii) प्लेटों के बीच के माध्यम पर-यह देखा गया है कि यदि संधारित्र की प्लेटों के मध्य का स्थान किसी कुचालक पदार्थ जैसे पैराफिन, मोम, तेल, अभ्रक आदि से भर दिया जाये तो संधारित्र की धारिता बढ़ जाती है, यदि प्लेटों के बीच की दूरी को स्थिर रखा जाये। अतः संधारित्र की धारिता का मान प्लेटों के बीच स्थित परावैद्युत माध्यम के परावैद्युतांक K के अनुक्रमानुपाती होता है। यदि संधारित्र की प्लेटों के मध्य वायु होने पर संधारित्र की धारिता C हो तो प्लेटों के मध्य K परावैद्युतांक का माध्यम होने पर संधारित्र की विद्युत धारिता KC हो जाती है। अर्थात् धारिता K गुनी बढ़ जाती है।

प्रश्न 32.
संधारित्रों के उपयोग को लिखिए ।
उत्तर:
(1) आवेश के संचायक के रूप में (As a charge Accumulator):
संधारित्र का मुख्य कार्य आवेश को संचित करना होता है। यदि हम किसी परिपथ में क्षणिक (Instantaneous) परन्तु शक्तिशाली वैद्युत धारा प्रवाहित करना चाहें तो परिपथ के सिरे को एक आवेशित संधारित्र से सम्बन्धित कर देते हैं। स्पंदित वैद्युत चुम्बक जो क्षणिक परन्तु तीव्र चुम्बकीय क्षेत्र उत्पन्न करने के लिए प्रयुक्त किये जाते हैं, आवेशित संधारित्रों से ही विद्युत-धारा प्राप्त करते हैं।

(2) विद्युत स्थितिज ऊर्जा संचित करने के लिए (For storing Electrostatic P.E):
संधारित्र द्वारा ऊर्जा संग्रहित करने की दर धीमी होती है जबकि ऊर्जा विसर्जन की प्रक्रिया अतिशीघ्र होती है। इसी गुण के आधार पर न्यून समय में फ्लश से (फलश) परिपथ में संधारित्र का उपयोग करके प्रकाश प्राप्त कर कैमरे में चित्र लिये जाते हैं।

(3) रेडियो व टीवी में (In Radio and T.V.):
रेडियो व टीवी की संचार प्रणाली में प्रयुक्त दो प्रमुख परिपथों (ट्रान्समीटर व रिसीवर) में संधारित्रों का उपयोग किया जाता है। उपयुक्त धारिता मान के संधारित्रों का उपयोग कर इन परिपथों में विद्युत चुम्बकीय दोलन उत्पन्न किये जाते हैं। दोलनों से उत्पन्न विद्युत चुम्बकीय तरंगों का उपयोग, संकेतों के प्रसारण में किया जाता है। संधारित्रों के उपयोगों से इच्छित आवृत्ति के रेडियो या टीवी संकेतों को प्राप्त किया जा सकता है।

(4) वैज्ञानिक अध्ययन में (In Scientific Study):
वैज्ञानिक अध्ययन में संधारित्र अत्यन्त उपयोगी सिद्ध हुए हैं। संधारित्र में भिन्नभिन्न आकार की प्लेटों का प्रयोग करके उनके मध्य भिन्न-भिन्न संरूपण (Configuration) के वैद्युत-क्षेत्र स्थापित किये जाते हैं। इन क्षेत्रों में विभिन्न परावैद्युत पदार्थ रखकर उनके व्यवहार के विषय में अध्ययन किया जाता है।

(5) चिकित्सा क्षेत्र में (In Medicine):
हृदय रोगी में छाती (Chest) पर विद्युत आघात (Electric shock) देकर हृदय की धड़कन को नियंत्रित किया जाता है। इस प्रक्रिया में जिस उपकरण का प्रयोग किया जाता है, उसे डेफिब्रीलेटर (defibrillator) कहते हैं। इसमें कई F कोटि की संधारित्र होती है, जिसे कई हजार वोल्ट पर आवेशित किया जाता है। संधारित्र में संचित ऊर्जा का उपयोग छाती पर विद्युत आघात देकर हृदय रोगी की हृदय मांसपेशियों की क्रियाप्रणाली को व्यवस्थित करते हैं, जो हृदय की धड़कन को नियंत्रित करने में सहायक होती है।

(6) विद्युत फिल्टरों में (In Electric Filters):
शक्तिप्रदाय स्रोतों में प्रयुक्त दिष्टकारी परिपथों से प्राप्त वोल्टता संकेत को smooth करने के लिए संधारित्रों का उपयोग किया जाता है। इसके अतिरिक्त श्रव्य यंत्रों में प्रयुक्त शक्ति प्रवर्धकों का युग्मन करने के लिए भी इनका उपयोग किया जाता है।

(7) कम्प्यूटर में (In Computers):
कम्प्यूटर के कुंजी पटल (Key Board) की कार्यप्रणाली धारिता के सिद्धान्त पर आधारित होती है। कुंजी पटल में कुंजी प्लैन्जर (Plunger) के एक सिरे पर स्थितं होती है। प्लैन्जर का दूसरा सिरा गतिक धातु की प्लेट से जुड़ा होता है। गतिक प्लेट को एक अन्य स्थिर प्लेट से परावैद्युत माध्यम के द्वारा अलग रखा जाता है, जिससे एक परिवर्तित संधारित्र की संरचना होती है। कुंजी को दबाने से प्लेटों के मध्य की दूरी कम होती है, जिससे धारिता के मान में वृद्धि होती है। इस परिवर्तन को कम्प्यूटर के इलेक्ट्रॉनिक परिपथों द्वारा संसूचित कर लिया जाता है। सूक्ष्म संधारित्रों का उपयोग कम्य्यूटरों में मैमोरी संग्रहित करने के लिए किया जाता है।

प्रश्न 33.
10 संधारित्र प्रत्येक की धारिता 10 μF है, को श्रेणी संयोजन तत्पश्चात् समान्तर संयोजन में जोड़ने पर तुल्य धारिताओं का गुणनफल लिखिए।
हल – n संधारित्रों के श्रेणी संयोजन की तुल्यधारिता
\(\frac{1}{\mathrm{C}_{\mathrm{S}}}=\frac{1}{\mathrm{C}_{\mathrm{I}}}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}+\ldots \ldots \cdot \frac{1}{\mathrm{C}_{\mathrm{n}}}\) होगी
यहाँ पर 10 संधारित्र जिनकी प्रत्येक की धारिता 10 μF है। इन सभी को श्रेणी संयोजन में जोड़ा गया है। इसलिये तुल्यधारिता का मान 1 μF होगा।
इन सभी को श्रेणी संयोजन के बाद समान्तर संयोजन में जोड़ा गया है।
समान्तर संयोजन के लिये तुल्यधारिता का सूत्र

आंकिक प्रश्न-

प्रश्न 1.
(a) आवेश 4 × 10^-7C के कारण इससे 9 cm दूरी पर स्थित किसी बिंदु P पर विभव परिकलित कीजिए।
(b) अब, आवेश 2 × 10^-9C को अनंत से बिंदु P तक लाने में किया गया कार्य ज्ञात कीजिए। क्या उत्तर जिस पथ के अनुदिश आवेश को लाया गया है उस पर निर्भर करता है?
हल-दिया गया है-
(a) Q = 4 × 10^-7C
r = 9 cm = 9 × 10^-2m.
V = \(\frac{1}{4 \pi \epsilon_o} \frac{Q}{r}\)
मान रखने पर V = \(\frac{9 \times 10^9 \times 4 \times 10^{-7}}{9 \times 10^{-2}}\)
V = 4 × 10⁴ Volt
(b) किया गया कार्य (W) = आवेश (q) × विभवान्तर (V)
W = 2 × 10^-9 × 4 × 10⁴
= 8 × 10^-5
नहीं, कार्य पथ पर निर्भर नहीं होगा।

प्रश्न 2.
एक वर्ग की प्रत्येक भुजा 90 सेमी. लम्बी है। इसके कोने पर क्रमशः -2,+3,-4 तथा +5 माइक्रो कूलॉम आवेश रखे हैं। वर्ग के केन्द्र पर विद्युत विभव ज्ञात कीजिये।
हल-माना कि 90 सेमी. भुजा वाला वर्ग ABCD है और जिसके शीर्ष A,B,C,D पर क्रमश: -2, 3, -4, +5 माइक्रो कूलॉम मान के आवेश रखे हुए हैं।
यहाँ AC और BD वर्ग के विकर्ण हैं जो O पर काटते हैं जो कि वर्ग का केन्द्र है। वर्ग के केन्द्र O पर विभव V₀ = वर्ग के शीर्षों पर रखे प्रत्येक आवेश के कारण उत्पन्न विभवों का बीजगणितीय योग
यहाँ पर (AC)² = (AB)² + (BC)²
(AC)² = (90)² + (90)² = 2 × (90)²
∴ AC = 90√2 सेमी.

प्रश्न 3.
एक बिन्दु आवेश के कारण किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता तथा वैद्युत विभव क्रमशः 30 न्यूटन/कूलॉम तथा 15 जूल/कूलॉम है। ज्ञात कीजिए कि
(i) प्रेक्षण बिन्दु से आवेश की दूरी तथा
(ii) आवेश का परिमाण।
हल-दिया है-
E = 30 न्यूटन/कूलॉम
V = 15 जूल/कूलॉम
(i) एक बिन्दु आवेश q के कारण इससे $r$ दूरी पर स्थित प्रेक्षण बिन्दु पर विद्युत क्षेत्र की तीव्रता

प्रश्न 4.
+10 μC एवं -10 μC के दो बिन्दु आवेश वायु में परस्पर 40 cm की दूरी पर रखे हैं।
(a) निकाय की वैद्युत स्थितिज ऊर्जा की गणना कीजिए। यह मान लीजिए कि अनन्त पर विद्युत स्थितिज ऊर्जा शून्य होती है।
(b) निकाय के लिए समविभव पृष्ठ खींचिये।
(c) निकाय के दोनों आवेशों को अनन्त तक दूर करने में कितना कार्य करना होगा?
हल-(a) दिया है-
q₁ = 10 μC = 10 × 10_-6C
q₂ = -10 μC = – 10 × 10_-6C
r₁₂ = 40 cm = 0. 40 m
दो आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा

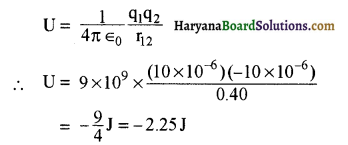
(b) अनुच्छेद 2.6 में देखें।
(c) जब दोनों आवेशों को एक-दूसरे से अलग करते हुए अनन्त तक विस्थापित किया जायेगा तो दोनों की वैद्युत स्थितिज ऊर्जा शून्य हो जायेगी अर्थात्
U₂ = 0
परन्तु U₁ = -2. 25 J
इसलिए दोनों को विस्थापित करने में किया गया कार्य
W = U₂ – U₁ = 0 – (- 2. 25)
= 2. 25 J

प्रश्न 5.
किसी बिन्दु P पर वैद्युत विभव V(x, y, z) = 6x -8xy² -8 y + 6yz – 4z²। मूल बिन्दु पर स्थित 4 कूलॉम बिन्दु आवेश पर वैद्युत बल ज्ञात कीजिए।
हल-हम जानते हैं-

प्रश्न 6.
10^-6 मीटर व्यास तथा 880.5 किलोग्राम/मीटर³ घनत्व वाली एक तेल बूँद 10 मिलीमीटर में पृथक्कृत प्लेटों के मध्य स्थिर रहती है। प्लेटों के मध्य विभवान्तर 36 वोल्ट है। तेल बूँद पर इलेक्ट्रॉनों की संख्या ज्ञात कीजिए।
g = 10 मीटर/सेकण्ड²
हल-दिया है-
घनत्व d₀ = 880.5 किग्रा./मी.³

प्रश्न 7.
तीन सर्वसम (एक-जैसे) संधारित्रों को श्रेणीक्रम में संयोजित करने (जोड़ने) पर उनकी तुल्य (कुल) धारिता 1 μF है। यदि
उन्हें पार्श्वक्रम (समान्तर क्रम) में संयोजित किया (जोड़ा) जाये, तो उनकी कुल धारिता कितनी होगी? यदि दोनों दशाओं (संयोजनों) में संधारित्रों को एक ही स्रोत से जोड़ा जाये तो इन दो प्रकार के संयोजनों में संचित ऊर्जा का अनुपात ज्ञात कीजिए।
हल-माना कि प्रत्येक संधारित्र की धारिता C μF है। इसलिए श्रेणीक्रम में संयोजन की स्थिति में

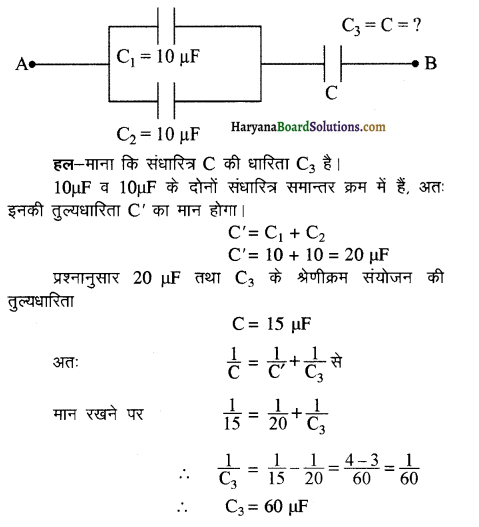
प्रश्न 8.
संधारित्र C की धारिता की गणना कीजिए यदि A व B के मध्य संयोजन की तुल्यधारिता 15 μF है।

प्रश्न 9.
चित्र में दर्शाये गये संयोजन की बिन्दु P व N के मध्य तुल्यधारिता ज्ञात कीजिए।.

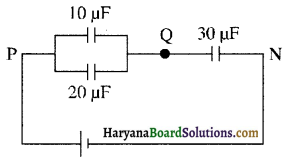
हल-यहाँ 10 μF व 20 μF मान के संधारित्र समान्तर क्रम में जुड़े हुए हैं, अतः इनकी तुल्यधारिता जुड़े हुए हैं, अतः इनकी तुल्यधारिता
C = (C₁ + C₂) से C = (10 + 20) = 30 μF होगी।
अतः इन संधारित्रों को बिन्दु P व N के मध्य अन्य 30 μF मान के एक संधारित्र से प्रतिस्थापित कर सकते हैं। यह प्रतिस्थापित संधारित्र; पहले से ही लगे हुए 30 μF संधारित्र के श्रेणीक्रम में है जैसा आगे के चित्र में दर्शाया गया है।

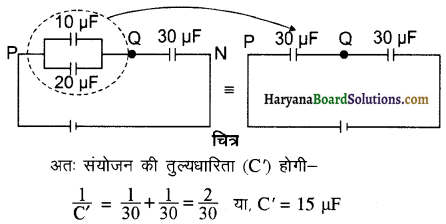
प्रश्न 10.
चित्र में दर्शाये गये संयोजन की बिन्दु P व N के मध्य तुल्यधारिता का मान ज्ञात कीजिए जबकि (अ) स्विच S खुला है, (ब) स्विच S बन्द है। यहाँ C₁ = 1 µF व C₂ = 2 µF हैं।
हल-(अ) दिये गये संयोजन में बिन्दु a व b के मध्य स्विच S खुला होने पर बिन्दु P व a के मध्य जुड़ी संधारित्र C_p बिन्दु a व N के मध्य जुड़ी संधारित्र C₁ के साथ श्रेणी संयोजन में होगी। इस संयोजन की तुल्यधारिता

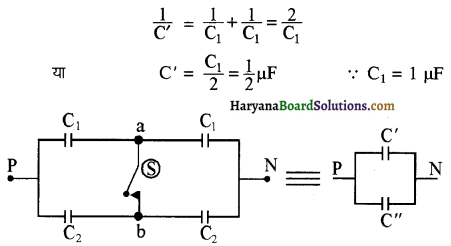
इसी प्रकार बिन्दु P व N के मध्य जुड़ी दोनों C₂ मान वाली संधारित्र भी श्रेणी संयोजन में हैं। इस संयोजन की तुल्यधारिता
\(\frac{1}{\mathrm{C}^{\prime \prime}}=\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_2}=\frac{2}{\mathrm{C}_2}\)
या C” = \(\frac{\mathrm{C}_2}{2}\) = 1 μF
∵ C₂ = 2 μF
अब बिन्दु P व N के मध्य संधारित्र C’ तथा C” परस्पर समान्तर संयोजन में हैं अतः तुल्यधारिता
C = \( \frac{1}{2}\) μF + 1 μF = \(\frac{3}{2}\) μF होगी।
(ब) बिन्दु a व b के मध्य स्विच S बन्द (on) होने पर ये बिन्दु समान विभव पर होंगे इसलिए संयोजन के दोनों खण्ड परस्पर श्रेणी क्रम में हो जायेंगे जिनमें प्रत्येक खण्ड की धारिता होगी-
C_t = C_tt = C_t + C_tt = 1 + 2 = 3 μF

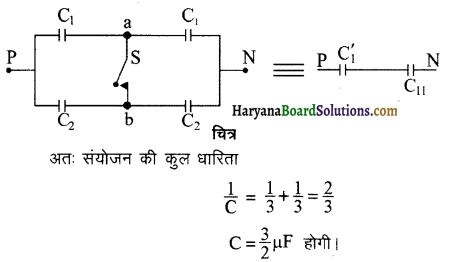
प्रश्न 11.
एक समान्तर पट्ट वायु संधारित्र की धारिता 8 μF है। इसकी प्लेटों के बीच की दूरी आध् कर दी जाती है तथा प्लेटों के बीच का स्थान 5 परावैद्युतांक वाले माध्यम से भर दिया जाता है। दूसरी स्थिति में संधारित्र की धारिता ज्ञात कीजिए।
हल-समान्तर पट्ट वायु संधारित्र की धारिता
C = \(\frac{\epsilon_0 A}{\mathrm{~d}}\) = 8 μF (दिया है,)
प्लेटों के बीच की दूरी आधी अर्थात् d/2 करने पर तथा प्लेटों के बीच का स्थान K = 5 परावैद्युतांक वाले माध्यम से भरने पर संधारित्र की धारिता
C_m = \(\mathrm{K}\left(\frac{\epsilon_0 \mathrm{~A}}{\mathrm{~d} / 2}\right)=2 \mathrm{~K}\left(\frac{\epsilon_0 \mathrm{~A}}{\mathrm{~d}}\right)\)
इसलिए C_m = 2K × C
मान रखने पर C_m = 2 × 5 × 8 μF = 80 μF

प्रश्न 12.
एक समान्तर पट्ट संधारित्र की दोनों प्लेटों के बीच की दूरी 4 मिमी. है। 3 पराव्द्युतांक वाली 3 मिमी. मोटी एक परावैद्युत पट्टी प्लेटों के बीच प्लेटों के समान्तर रख दी जाती है। प्लेटों के बीच की दूरी इस प्रकार व्यवस्थित की जाती है कि संधारित्र की धारिता प्रारम्भिक धारिता की 2/3 हो जाती है। प्लेटों के बीच नई दूरी क्या है?
हल-दिया गया है-प्रारम्भिक संधारित्र की धारिता का सूत्र,
C = \(\frac{\epsilon_0 \mathrm{~A}}{\mathrm{~d}}\)
यदि प्लेटों के बीच परावैद्युत रखने पर, इनके बीच नई दूरी d₁ हो तो प्रश्नानुसार, संधारित्र की नई धारिता = \(\left(\frac{2}{3}\right)\) बिना परावैद्युत संधारित्र की प्रारम्भिक धारिता
परावैद्युत पट्टी रखने के उपरान्त धारिता का सूत्र

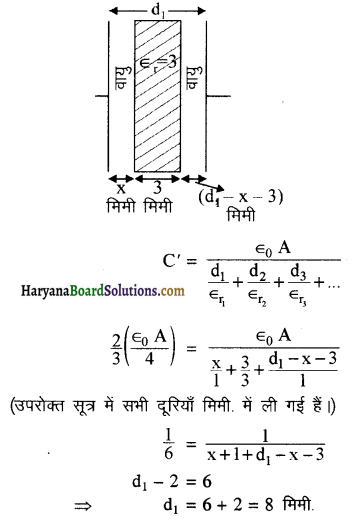
प्रश्न 13.
C धारिता वाले अनेक संधारित्र चित्र में दर्शाये अनुसार अनन्त संख्या में संयोजित हैं। बिन्दु A व B के मध्य कुल धारिता का मान ज्ञात कीजिए।
हल-चूँकि श्रेणी अनन्त लम्बाई की है, अतः बिन्दुओं P व a के दाहिनी ओर की श्रेणी की धारिता का मान उतना ही होगा जो श्रेणी के बिन्दुओं A व B के दाहिनी ओर है। यदि श्रेणी की तुल्यधारिता C₁ हो तो दिये गये चित्र के संयोजन को नीचे दिये गये चित्र द्वारा प्रतिस्थापित
कर सकते हैं। इस प्रकार A व B के मध्य तुल्यधारिता \(\left[\mathrm{C}+\frac{\mathrm{CC}_1}{\mathrm{C}+\mathrm{C}_1}\right]\)
होगी। परन्तु धारिता का यह मान मूल श्रेणी की तुल्यधारिता C₁ के ही बराबर है। अतः

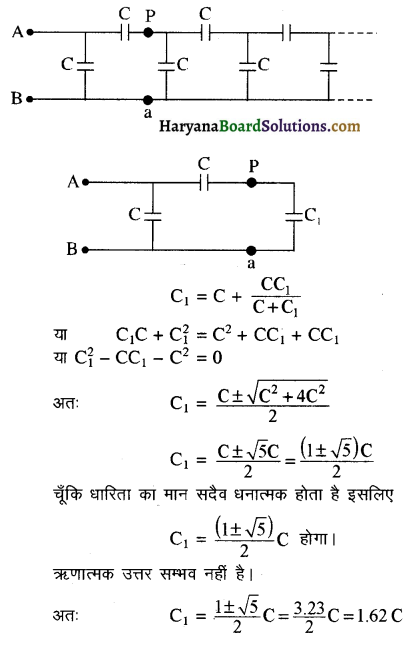
प्रश्न 14.
एक गोलाकार संधारित्र के गोलों के बीच भरे माध्यम का परावैद्युतांक 7 है। इसके गोलों की त्रिज्यायें क्रमशः 50 सेमी. तथा 60 सेमी. हैं। संधारित्र की धारिता का मान ज्ञात कीजिए।
हल-गोलीय संधारित्र के आन्तरिक गोले की त्रिज्या a = 50 सेमी. = 0.50 मीटर, बाह्य गोले की त्रिज्या b = 60 सेमी. = 0.60 मीटर तथा दोनों गोलों के बीच माध्यम का परावैद्युतांक K = 7 इसलिए गोलीय संधारित्र की धारिता

प्रश्न 15.
समान्तर पट्ट वायु संधारित्र की धारिता 10 μF है। इस संधारित्र को चित्र के अनुसार दो बराबर भागों में विभाजित करके \(\epsilon_{r_1}=2\) तथा \(\epsilon_{\boldsymbol{r}_2}=4\) परावैद्युतांक वाले माध्यम से भर दिया जाता है। इस निकाय की धारिता का मान ज्ञात कीजिए।

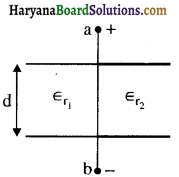
हल-यहाँ पर प्रत्येक भाग को एक संधारित्र के तुल्य लिया जा सकता है। दोनों संधारित्रों की ऊपर वाली प्लेटें बैटरी के धनाग्र से व नीचे की प्लेटें ऋणाग्र से जुड़ी हैं। अतः कल्पित दोनों संधारित्रों को परस्पर समान्तर संयोजन में जुड़ा मानकर प्रथम संधारित्र की धारिता
C₁ = द्वितीय संधारित्र की धारिता C₂ = \(\frac{\epsilon_{\mathrm{r}_2} \in_0 \mathbf{A} / 2}{\mathrm{~d}}\) अतः संयोजन की कुल धारिता

प्रश्न 16.
4 सेमी. व 7 सेमी. के दो चालक गोलों पर आवेश की मात्राएँ क्रमशः 500 माइक्रो कूलॉम और 60 माइक्रो कूलॉम हैं। चालकों को परस्पर जोड़ने पर विद्युत स्थितिज ऊर्जा हानि की गणना कीजिए।
हल-निकाय की कुल प्रारम्भिक विद्युत ऊर्जा

प्रश्न 17.
दो समान आवेश घनत्व वाले चालकों A तथा B की त्रिज्याएँ क्रमशः R₁ व R₂ (R₁ >R₂) हैं। चालकों को नगण्य धारिता के चालक तार से जोड़ा जाता है तो ज्ञात कीजिए-
(अ) आवेश किस चालक से किसकी ओर प्रवाहित होगा?
(ब) आवेश पुनर्वितरण के पश्चात् चालकों पर आवेश का अनुपात क्या होगा?
हल-(अ) यदि आवेश पुनर्वितरण से पूर्व चालकों A व B पर

समीकरण (iii) से \(\frac{\mathrm{Q}_1}{\mathrm{Q}_2}\) का मान रखने पर
यहाँ R₁ > R₂ है, अतः गोले A पर विभव का मान (V₁) गोले B पर विभव के मान (V₂) से अधिक होगा। अतः आवेश; उच्चविभव के चालक A से निम्न विभव के चालक B की ओर प्रवाहित होगा।
(ब) आवेश पुनर्वितरण के पश्चात् गोलों पर आवेश की मात्राओं का अनुपात उनकी धारिताओं के अनुपात के तुल्य होगा। अर्थात
\(\frac{Q_1}{Q_2}=\frac{C_1}{C_2}=\frac{4 \pi \epsilon_0 R_1}{4 \pi \epsilon_0 R_2}=\frac{R_1}{R_2}\)

प्रश्न 18.
एक अनावेशित संधारित्र को बैटरी से जोड़ा जाता है। दर्शाइये कि संधारित्र को आवेशित करने के लिए बैटरी द्वारा प्रयुक्त की गई ऊर्जा का आधा भाग ऊष्मा के रूप में क्षय होता है।
हल-किसी V विद्युत वाहक बल की बैटरी द्वारा C धारिता के संधारित्र को Q आवेश से आवेशित करने के लिए बैटरी द्वारा किये गये कार्य का मान W = QV होगा।
वस्तुतः यह कार्य बैटरी द्वारा संधारित्र को आवेशित करने की प्रक्रिया में खर्च की गई ऊर्जा है। इसमें जो ऊर्जा संधारित्र में संचित ऊर्जा के तुल्य होगी, वह है U = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\)QV
तथा शेष ऊर्जा = QV – \(\frac{1}{2}\)QV = \(\frac{1}{2}\)QV जो ऊष्मा के रूप में क्षय हो जायेगी। अतः बैटरी द्वारा आवेशन प्रक्रिया में खर्च की गई ऊर्जा का आधा भाग ऊष्मा के ऊर्जा के रूप में क्षय होता है।

प्रश्न 19.
समान धारिता की दो संधारित्र चित्रानुसार (चित्र) एक बैटरी से जुड़ी हुई हैं। स्विच S प्रारम्भ में बन्द अवस्था में है। अब स्विच S को खुला कर संधारित्र की प्लेटों के मध्य ∈^r = 3 परावैद्युतांक के पदार्थ को भरा जाता है। परावैद्युत पदार्थ को रखने से पूर्व व उसके पश्चात् संधारित्रों में संग्रहित विद्युत ऊर्जा के मानों का अनुपात ज्ञात कीजिए।

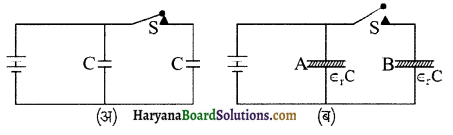
हल-प्रारम्भ में स्विच S बन्द होने पर दोनों संधारित्रों के समान्तर क्रम में जुड़े होने के कारण, ये दोनों समान विभव V पर होंगे।
अर्थात् = U_i = \(\frac{1}{2}\)C₁V²
= \(\frac{1}{2}\)(C₁ + C₂) V² = CV² ………..(i)
जब स्विच S को खुला रखकर संधारित्र की प्लेटों के मध्य परावैद्युत पदार्थ रखा जाता है तब प्रत्येक संधारित्र की धारिता ∈_r गुणा हो जायेगी और चूँकि संधारित्र A अब भी बैटरी से जुड़ा है। अतः इस पर विभवान्तर का मान प्रारम्भिक विभवान्तर के मान V के तुल्य होगा जबकि संधारित्र B पर विभवान्तर का नया मान V’ = [/latex]\frac{\mathrm{V}}{\epsilon_{\mathrm{r}}}[/latex] हो जायेगा एवं आवेश स्थिर रहेगा। अतः इस स्थिति में निकाय की विद्युत ऊर्जा होगी-

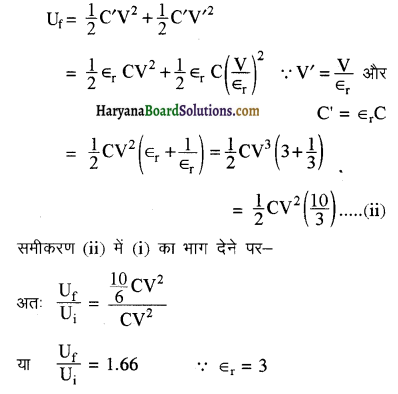
प्रश्न 20.
X एवं Y दो समान्तर प्लेट संधारित्र हैं, जिनकी प्लेटों का क्षेत्रफल एवं उनके बीच की दूरी समान है। X की प्लेटों के मध्य वायु है और Y की प्लेटों के मध्य K = 5 परावैद्युतांक वाला परावैद्युत माध्यम है। (चित्र में)
(a) X एवं Y की प्लेटों के मध्य विभवान्तर की गणना कीजिए।
(b) X एवं Y में संचित वैद्युत स्थितिज ऊर्जाओं का अनुपात क्या है?

हल-(a) वायु संधारित्र X की धारिता

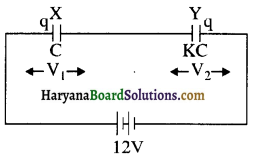
प्रश्न 21.
चित्र में दर्शाए अनुसार तीन परिपथों, जिनमें प्रत्येक स्विच S और दो संधारित्र लगे हैं, को प्रारम्भ में आवेशित किया जाता है। स्विच को बन्द करने पर किस परिपथ में बार्यी ओर दिए गए संधारित्र में आवेश
(i) बढ़ेगा,
(ii) घटेगा और
(iii) अपरिवर्तित रहेगा? कारण दीजिए।

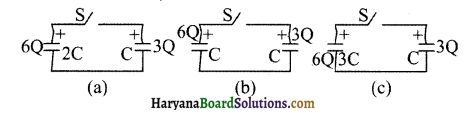
हल-आवेश संरक्षण के नियम से
माना q₁ तथा q₂ दो आवेश हैं जो कि संधारित्र के बायीं तरफ तथा दायीं तरफ है।

अतः बायें संधारित्र पर आवेश का मान अपरिवर्तित रहता है।
(b) दूसरे परिपथ के लिये
6Q + 3Q = CV + CV
उभयनिष्ठ विभवान्तर, V = \(\frac{9 \mathrm{Q}}{2 \mathrm{C}}\)
स्विच (S) की बन्द करने के बाद बायें संधारित्र पर संधारित्र का मान
q₁ = CV
= C × \(\frac{9 \mathrm{Q}}{2 \mathrm{C}}\) = 4.5 Q
इसलिये परिपथ (b) में बायें संधारित्र पर आवेश का मान घटेगा।