HBSE 10th Class Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.1

Haryana State Board HBSE 10th Class Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Exercise 5.1

प्रश्न 1.
निम्नलिखित स्थितियों में से किन स्थितियों में संबद्ध संख्याओं की सूची AP है और क्यों?
(i) प्रत्येक किलोमीटर के बाद का टैक्सी का किराया, जबकि प्रथम किलोमीटर के लिए किराया 15 रु० है और प्रत्येक अतिरिक्त किलोमीटर के लिए किराया 8 रु० है।
(ii) किसी बेलन (cylinder) में उपस्थित हवा की मात्रा, जबकि वायु निकालने वाला पंप प्रत्येक बार बेलन की शेष हवा का 1/4 भाग बाहर निकाल देता है।
(ii) प्रत्येक मीटर की खुदाई के बाद, एक कुआँ खोदने में आई लागत, जबकि प्रथम मीटर खुदाई की लागत 150 रु० है और बाद में प्रत्येक मीटर खुदाई की लागत 50 रु० बढ़ती जाती है।
(iv) खाते में प्रत्येक वर्ष का मिश्रधन, जबकि 10000 रु० की राशि 8% वार्षिक की दर से चक्रवृद्धि ब्याज पर जमा की जाती है।
हल :
(i) यहाँ पर, प्रथम 1 कि०मी० का टैक्सी का किराया = 15 रु०
प्रत्येक अतिरिक्त 1 कि०मी० का टैक्सी का किराया = 8 रु०
अतः टैक्सी का 1 कि०मी०, 2 कि०मी०, 3 कि०मी०, 4 कि०मी० इत्यादि का क्रमशः किराया
= 15 रु०, 23 रु०, 31 रु०, 39 रु०……………..
इस प्रकार संबंध संख्याओं की सूची = 15, 23, 31, 39….
∵ सार्व अंतर (d) = 23 – 15 = 8
अतः संबंध संख्याओं की सूची AP है जिसका सार्व अंतर 8 है।

(ii) यहाँ पर, माना बेलन में उपस्थित हवा की मात्रा = Vm³

क्योंकि क्रमागत संख्याओं में समान अंतर नहीं है।
इसलिए संबंध संख्याओं की सूची AP में नहीं है।

(iii) यहाँ पर, प्रथम 1 मी० कुएँ की खुदाई का व्यय = 150 रु०
प्रत्येक अतिरिक्त 1 मी० कुएँ की खुदाई का व्यय = 50 रु०
अतः कुएँ की खुदाई का 1 मी०, 2 मी०, 3 मी०, 4 मी० ………….. इत्यादि का व्यय
= 150 रु०, 200 रु०, 250 रु०, 300 रु०…….
इस प्रकार संबंध संख्याओं की सूची = 150, 200, 250, 300…
सार्व अंतर (d) = 200 – 150 = 50
अतः संबंध संख्याओं की सूची AP है जिसका सार्व अंतर 50 है।

(iv) यहाँ पर,
मूलधन = 10,000 रु०
दर = 8% वार्षिक

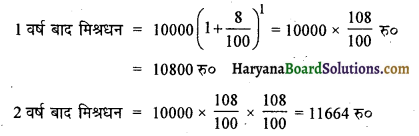
3 वर्ष बाद मिश्रधन = 10000 x \(\frac{108}{100} \times \frac{108}{100} \times \frac{108}{100}\) = 12597.12 रु०
अतः संबंध संख्याओं की सूची = 10800, 11664, 12597.12 …………
यहाँ पर 11664 – 10800 = 864
तथा 12597.12 – 11664 = 933.12
864 ≠ 933.12
क्योंकि क्रमागत संख्याओं में समान अंतर नहीं है।
इसलिए संबंध संख्याओं की सूची AP में नहीं है।

प्रश्न 2.
दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अंतर d निम्नलिखित हैं-
(i) a= 10, d = 10
(ii) a =-2, d = 0
(iii) a = 4, d = -3
(iv) a =-1, d = 1/2
(v) a = -1.25, d = -0.25
हल :
(i) यहाँ पर
प्रथम पद (a) = 10
सार्व अंतर (a) = 10
a₂ = a + 1d = 10 + 10 = 20
a₃ = a + 2d = 10 + 2 x 10 = 30
a₄ = a + 3d = 10 + 3 x 10 = 40
अतः AP के प्रथम चार पद = 10, 20, 30, 40

(ii) यहाँ पर
प्रथम पद (a) = -2
सार्व अंतर (a) = 0
a₂ = a + 1d = -2 + 1 x 0 = -2
a₃ = a + 2d = -2 + 2 x 0 = -2
a₄ = a + 3d = -2 + 3 x 0 = -2
अतः AP के प्रथम चार पद = -2,-2,-2,-2

(iii) यहाँ पर
प्रथम पद (a) = 4
सार्व अंतर (d) = -3
a₂ = a + 1d = 4 + 1(-3)= 4 – 3 = 1
a₃ = a + 2d = 4 + 2(-3) = 4 – 6 = -2
a₄ = a+ 3d = 4 + 3(-3) = 4 – 9 = -5
अतः AP के प्रथम चार पद = 4, 1,-2,-5

(iv) यहाँ पर
प्रथम पद (a) = -1
सार्व अंतर (d) = 1/2

अतः AP के प्रथम चार पद =-1, –\(\frac{1}{2}\), 0, \(\frac{1}{2}\)

(v) यहाँ पर
प्रथम पद (a) = -1.25
सार्व अंतर (d) = -0.25
a₂ = a + 1d = -1.25 +1 (-0.25) = –1.50
a₃ = a+2d = -1.25 + 2 (-0.25) = -1.75
a₄ = a + 3d = -1.25 + 3 (-0.25) = -2.00
अतः AP के प्रथम चार पद = -1.25, -1.50,-1.75, -2.00

प्रश्न 3.
निम्नलिखित में से प्रत्येक AP के लिए प्रथम पद तथा सार्व अंतर लिखिए
(i) 3, 1, -1, -3, …………
(ii) -5,-1, 3, 7, ………. …. 1 5 9 13
(iii) \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}\)
(iv) 0.6, 1.7, 2.8, 3.9, ……..
हल :
(i) यहाँ पर दी गई
AP = 3,1,-1,-3, …………
प्रथम पद (a) = 3
सार्व अंतर (d) = 1-3 = -2
अतः = 3 व d= – 2

(ii) यहाँ पर दी गई
AP = -5, -1, 3, 7, …………
प्रथम पद (a) = -5
सार्व अंतर (d) = -1 – (-5) = -1 + 5 = 4
अतः a = -5 व d = 4

(iii) यहाँ पर दी गई

(iv) यहाँ पर दी गई
AP = 0.6, 1.7, 2.8, 3.9,
प्रथम पद (a) = 0.6
सार्व अंतर (d) = 1.7-0.6 = 1.1
अतः a = 0.6 व d = 1.1

प्रश्न 4.
निम्नलिखित में से कौन-कौन AP हैं? यदि कोई AP है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
(i) 2, 4, 8, 16, …………
(ii) 2,\(\frac{5}{2}\),3, \(\frac{7}{2}\), ……….
(iii) -1.2,-3.2, -5.2, -7.2, ……………………
(iv) -10, -6, -2, 2, …………
(v) 3,3 + -2 , 3 + 272, 3 + 3-12,………
(vi) 0.2, 0.22, 0.222, 0.2222, ………………
(vii) 0, -4, -8, –12, ………….
(viii) \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\)
(ix) 1, 3, 9, 27, ……
(x) a, 2a, 3a, 4a, …….
(xi) a, a², a³, a⁴, ……
(xii) 12, 18, 18, 132 ,…..
(xiii) √3, √6, √9, √2 , ………
(xiv) 1², 3²,5²,7², …………………………
(xv) 1²,5²,7², 73 ……………
हल :
(i) यहाँ पर दिया गया अनुक्रम है-2, 4, 8, 16, …………
a₂ – a₁ = 4 – 2 = 2
a₃ – 4₂ = 8 – 4 =4
a₄ – a₃ = 16 – 8 = 8
`क्योंकि दो क्रमागत पदों का अंतर समान नहीं है।
इसलिए दिया गया अनुक्रम AP नहीं है।

(ii) यहाँ पर दिया गया अनुक्रम है-2,\(\frac{5}{2}\),3, \(\frac{7}{2}\), ……….

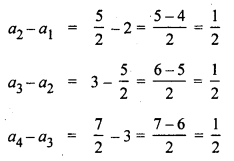
क्योंकि दो क्रमागत पदों का अंतर समान है।
अतः दिया गया अनुक्रम AP है, जिसका सार्व अंतर (d) =\(\frac{1}{2}\)
AP के अगले तीन पद होंगे
a₅ = a + 4d = 2 + 4 x \(\frac{1}{2}\) = 2 + 2 = 4
a₆ = a + 5d = 2 + 5 x \(\frac{1}{2}\) = \(\frac{4+5}{2}=\frac{9}{2}\)
a₇ = a + 6d = 2 +6 x \(\frac{1}{2}\) = 2 + 3 = 5

(iii) यहाँ पर दिया गया अनुक्रम है- -1.2,-3.2, -5.2, -7.2, ……………………
a₂ – a₁ = -3.2 – (-1.2) = -3.2 + 1.2 = 2.0
a₃ – a₂ = -5.2 -(-3.2)=-5.2 + 3.2 = -2.0
a₄ – a₃ = -7.2 – (-5.2) = -7.2 + 5.2 = -2.0
क्योंकि दो क्रमागत पदों का अंतर समान है।
अतः दिया गया अनुक्रम AP है, जिसका सार्व अंतर (d) = -2
AP के अगले तीन पद होंगे
a₅ = a + 4d = -1.2 + 4(-2) = -1.2 – 8 = -9.2
a₆ = a+ 5d = -1.2 + 5(-2) = -1.2 – 10 = -11.2
a₇ = a + 6d = -1.2 + 6(-2) = -1.2 – 12 = -13.2

(iv) यहाँ पर दिया गया अनुक्रम है- -10, -6, -2, 2, …………
a₂ – a₁ = -6-(-10) = -6 + 10 = 4
a₃ – a₂ = -2 -(-6) = -2 + 6 = 4
a₄ – a₃ = 2 – (-2)= 2 + 2 = 4
क्योंकि दो क्रमागत पदों का अंतर समान है।
अतः दिया गया अनुक्रम AP है, जिसका सार्व अंतर (d) = 4
AP के अगले तीन पद होंगे
a₅ = a +4d = -10 + 4(4) = -10 + 16 = 6
a₆ = a+ 5d = -10 + 5(4) = -10 + 20 = 10
a₇ = a + 6d = -10 + 6(4) = -10 + 24 = 14

(v) यहाँ पर दिया गया अनुक्रम है- 3,3 + -2 , 3 + 272, 3 + 3-12,………
a₂ – a₁ = (3 + √2)-3 = 3 + √2 – 3 = √2
a₃ – a₂ = (3 + 2√2)- (3 + √2) = 3 + 2√2 -3 – √2 = √2
a₄ – a₃ = (3 + 3√2)- (3 + 2√2) = 3 +3√2 – 3 – 2√2 = √2
क्योंकि दो क्रमागत पदों का अंतर समान है।
अतः दिया गया अनुक्रम AP है, जिसका सार्व अंतर (d) = √2
AP के अगले तीन पद होंगे
a₅ = a +4d = 3 +4√2
a₆ = a+ 5d = 3 + 5√2
a₇ = a + 6d = 3 + 6√2

(vi) यहाँ पर दिया गया अनुक्रम है-0.2, 0.22, 0.222, 0.2222, ………………
a₂ – a₁ = 0.22 – 0.2 = 0.02
a₃ – a₂ = 0.222 – 0.22 = 0.002
a₄ – a₃ = 0.2222 – 0.222 = 0.0002
क्योंकि दो क्रमागत पदों का अंतर समान नहीं है।
इसलिए दिया गया अनुक्रम AP नहीं है।

(vii) यहाँ पर दिया गया अनुक्रम है- 0, -4, -8, –12, ………….
a₂ – a₁ = -4 – 0 = -4
a₃ – a₂ = -8 -(-4) = -8 + 4 =-4
a₄ – a₃ = -12 – (-8) = -12 + 8 = -4
क्योंकि दो क्रमागत पदों का अंतर समान है।
अतः दिया गया अनुक्रम AP है, जिसका सार्व अंतर (d) = -4
AP के अगले तीन पद होंगे
a₅ = a + 4d = 0 + 4(-4)= –16
a₆ = a + 5d = 0 + 5(-4) = -20
a₇ = a + 6d = 0 + 6(-4)= -24

(viii) यहाँ पर दिया गया अनुक्रम है- \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\)

क्योंकि दो क्रमागत पदों का अंतर समान है।
अतः दिया गया अनुक्रम AP है, जिसका सार्व अंतर (d) = 0
AP के अगले तीन पद होंगे
a₅ = a + 4d = –\(\frac{1}{2}\) + 4(0) = –\(\frac{1}{2}\)
a₆ = a + 4d = –\(\frac{1}{2}\) + 5(0) = –\(\frac{1}{2}\)
a₇ = a + 6d = 1 + 6(0) = –\(\frac{1}{2}\) + 6(0) = –\(\frac{1}{2}\)

(ix) यहाँ पर दिया गया अनुक्रम है-1, 3, 9, 27, ……
a₂ – a₁ = 3 – 1 = 2
a₃ – a₂ = 9 – 3 = 6
a₄ – a₃ = 27 – 9 = 18
क्योंकि दो क्रमागत पदों का अंतर समान नहीं है।
इसलिए दिया गया अनुक्रम AP नहीं है।

(x) यहाँ पर दिया गया अनुक्रम है- a, 2a, 3a, 4a, …….
a₂ – a₁ = 2a – a = a
a₃ – a₂ = 3a – 2a = a
a₄ – a₃ = 4a – 3a = a
क्योंकि दो क्रमागत पदों का अंतर समान है।
अतः दिया गया अनुक्रम AP है, जिसका सार्व अंतर (d) = a
AP के अगले तीन पद होंगे
a₅ = a + 4d = a + 4(a) = 5a
a₆ = a + 5d = a + 5(a) = 6a
a₇ = a + 6d = a + 6(a) = 7a

(xi) यहाँ पर दिया गया अनुक्रम है-a, a², a³, a⁴, ……
a₂ – a₁ = a² – a = a(a-1)
a₃ – a₂ = a³ – a² = a²(a-1)
a₄ – a₃ = a⁴ – a³ = a³(a-1)
क्योंकि दो क्रमागत पदों का अंतर समान नहीं है।
इसलिए दिया गया अनुक्रम AP नहीं है।

(xii) यहाँ पर दिया गया अनुक्रम है- 12, 18, 18, 132 ,…..
a₂ – a₁ = √8 – √2 = 2√2 – √2 = 2
a₃ – a₂ = √18 – √8 = 3√2 – 2√2 = 12
a₄ – a₃ = √32 – √18 = 4√2 – 3√2 = 2
क्योंकि दो क्रमागत पदों का अंतर समान है। अतः दिया गया अनुक्रम AP है, जिसका सार्व अंतर (d) = √2
AP के अगले तीन पद होंगे-
a₅ = a +4d = √2 + 4(√2) = 5√2 = √50
a₆ = a + 5d. = √2 + 5(√2) = 6√2 = √72
a₇ = a + 6d = √2 + 6(√2) = 7√2 = √98

(xiii) यहाँ पर दिया गया अनुक्रम है- √3, √6, √9, √2 , ………
a₂ – a₁ = √6 – √3 = √3 (√2 – 1)
a₃ – a₂ = √9 – √6 = √3 (√3 – √2)
a₄ – a₃ = √12 – √5 = 2√3 -3
क्योंकि दो क्रमागत पदों का अंतर समान नहीं है।
इसलिए दिया गया अनुक्रम AP नहीं है।।

(xiv) यहाँ पर दिया गया अनुक्रम है-1², 3²,5²,7², …………………………
= 1, 9, 25, 49,.. ……..
a² – a¹ = 9 – 1 = 8
a³ – a² = 25 – 9 = 16
a⁴ – a³ = 49 – 25 = 24
क्योंकि दो क्रमागत पदों का अंतर समान नहीं है।
इसलिए दिया गया अनुक्रम AP नहीं है।

(xv) यहाँ पर दिया गया अनुक्रम है – 1²,5²,7², 73 ……………
= 1, 25, 49,73……
a² – a¹ = 25 – 1 = 24
a³ – a² = 49 – 25 = 24
a⁴ – a³ = 73 – 49 = 24
क्योंकि दो क्रमागत पदों का अंतर समान है।
अतः दिया गया अनुक्रम AP है, जिसका सार्व अंतर (d) = 24
AP के अगले तीन पद होंगे-
a⁵ = a + 4d = 1 + 4(24)= 1 + 96 = 97
a⁶ = a + 5d = 1 + 5(24) = 1 + 120 = 121
a⁷ = a + 6d = 1+ 6(24) = 1 + 144 = 145