Haryana State Board HBSE 7th Class Maths Solutions Chapter 1 पूर्णांक Ex 1.1 Textbook Exercise Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 1 पूर्णांक Ex 1.1
प्रश्न 1.
किसी विशिष्ट दिन विभिन्न स्थानों के तापमानों को डिग्री सेल्सियस (°C) में निम्नलिखित संख्या रेखा द्वारा दर्शाया गया है:

(a) इस संख्या रेखा को देखिए और इस पर अंकित स्थानों के तापमान लिखिए।
(b) उपर्युक्त स्थानों में से सबसे गर्म और सबसे ठण्डे स्थानों के तापमानों में क्या अन्तर है?
(c) लाहुलस्पीती एवं श्रीनगर के तापमानों में क्या अन्तर है?
(d) क्या हम कह सकते हैं कि शिमला और श्रीनगर के तापमानों का योग शिमला के तापमान से कम है? क्या इन दोनों स्थानों के तापमानों का योग श्रीनगर के तापमान से भी कम है?
हल :
(a) दी गई संख्या रेखा पर अंकित स्थानों के तापमान:
| स्थान | तापमान |
| लाहुलस्पीती | – 8°C |
| श्रीनगर | -2°C |
| शिमला | 5°C |
| ऊटी | 14°C |
| बैंगलोर | 22°C |
स्थान तापमान स्थान तापमान लाहुलस्पीती – 8°C ऊटी श्रीनगर -2°C . बैंगलोर 22°C शिमला 5°C
(b) बैंगलोर सबसे गर्म (22°C) तथा सबसे ठण्डा लाहुलस्पीती (-8°C) है तथा इनका तापान्तर = 22°C(-8°C) = 22°C + 8°C = 30°C है।
(c) लाहुलस्पीती तथा श्रीनगर के तापमानों में अन्तर – 2°C – (-8°C) = -2°C + 8°C = 6°C
(d) हाँ, श्रीनगर तथा शिमला के तापमानों का योग शिमला के तापमान से कम है।
-2°C + 5°C = 3°C तथा 3°C <5°C
यह तापमान श्रीनगर के तापमान से कम नहीं है।
![]()
प्रश्न 2.
किसी प्रश्नोत्तरी में सही उत्तर के लिए धनात्मक अंक दिए जाते हैं और गलत उत्तर के लिए ऋणात्मक अंक दिए जाते हैं। यदि पाँच उत्तरोत्तर चक्करों (rounds) में जैक द्वारा प्राप्त किए गए अंक 25, -5, -10, 15 और 10 थे, तो बताइए अन्त में उसके अंकों का कुल योग कितना था?
हल :
जैक द्वारा पाँच क्रमागत चक्करों में प्राप्त अंक 25, -5, -10, 15 और 10 थे।
जैक द्वारा प्राप्तांकों का कुल योग = 25 + (-5) + (-10) + 15 + 10
= 25 – 5 – 10 + 15 + 10
= 50 – 15 = 35 उत्तर
प्रश्न 3.
सोमवार को श्रीनगर का तापमान -5°C था और मंगलवार को तापमान 2°C कम हो गया। मंगलवार को श्रीनगर का तापमान क्या था? बुधवार को तापमान 4°C बढ़ गया। बुधवार को तापमान कितना था?
हल :
सोमवार को श्रीनगर का तापमान = -5°C
मंगलवार को तापमान 2°C कम हो गया तो मंगलवार | का तापमान = (- 5 – 2)°C = -7°C उत्तर
बुधवार के तापमान में वृद्धि 4°C तो बुधवार का | तापमान = (- 7+ 4)°C = -3°C उत्तर
प्रश्न 4.
एक हवाई जहाज समुद्र तल से 5000 मीटर की ऊँचाई पर उड़ रहा है। एक विशिष्ट बिन्दु पर यह हवाई जहाज समुद्र तल से 1200 मीटर नीचे तैरती हुई पनडुब्बी के ठीक ऊपर है। पनडुब्बी और हवाई जहाज के. बीच की ऊर्ध्वाधर दूरी कितनी है?
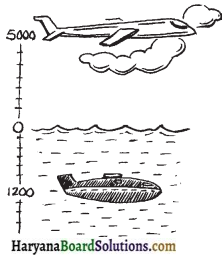
हल :
हवाई जहाज तथा पनडुब्बी के मध्य ऊर्ध्वाधर दूरी
= 5000m – (-1200) m
=5000 m + 1200 m
= 6200 m उत्तर
![]()
प्रश्न 5.
मोहन अपने बैंक खाते में 2000 रुपये जमा करता है और अगले दिन इसमें से 1642 रुपये निकाल लेता है। यदि खाते में से निकाली गई राशि को ऋणात्मक संख्या से निरूपित किया जाता है, तो खाते में जमा की गई राशि को आप कैसे निरूपित करोगे? निकासी के पश्चात् मोहन के खाते में शेष राशि ज्ञात कीजिए।
हल :
बैंक खाते में जमा की गई राशि को धनात्मक पूर्णाक से प्रदर्शित करेंगे।
निकासी के पश्चात् मोहन के खाते में शेष राशि = (+2000 रु.) + (-1642 रु.)
= (2000 – 1642) रु.
= 358 रु. उत्तर
प्रश्न 6.
रीता बिन्दु A से पूर्व की ओर बिन्दु B तक 20 किलोमीटर की दूरी तय करती है। उसी सड़क के अनुदिश बिन्दु B से वह 30 किलोमीटर की दूरी पश्चिम की ओर तय कस्ती है। यदि पूर्व की ओर तय की गई दूरी को धनात्मक पूर्णांक से निरूपित किया जाता है, तो पश्चिम की ओर तय की गई दूरी को आप कैसे निरूपित करोगे? बिन्दु A से उसकी अन्तिम स्थिति को किस पूर्णांक से निरूपित करोगे?

हल :
पश्चिम की ओर तय की गई दूरी को ऋणात्मक संख्या से निरूपित करेंगे। रीता द्वारा तय की गई दूरी का चित्रण :
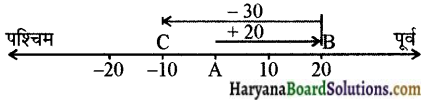
रीता बिन्दु A से 20 किलोमीटर दूर पूर्व की ओर बिन्दु B तक पहुँचती है तथा B से पश्चिम की ओर 30 किलोमीटर उसी सड़क के सहारे जाती है।
अत: A से उसकी अन्तिम स्थिति (-10) किलोमीटर होगी। यह पूर्णांक – 10 से प्रदर्शित किया जायेगा। उत्तर
प्रश्न 7.
किसी मायावी वर्ग में प्रत्येक पंक्ति, प्रत्येक स्तम्भ एवं प्रत्येक विकर्ण की संख्याओं का योग समान होता है। बताइए निम्नलिखित में से कौनसा वर्ग एक मायावी वर्ग है?
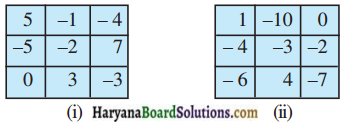
हल :
(i) प्रथम वर्ग में :
प्रथम पंक्ति : 5 + (-1) + (-4) = 5 – 1 – 4 = 0
द्वितीय पंक्ति : (-5) + (-2) + 7
= – 5 – 2 + 7 = 0
तृतीय पंक्ति : 0 + 3 + (-3)= 0 + 3 – 3 = 0
प्रथम स्तम्भ : 5 + (-5) + 0 = 5 – 5 + 0 = 0
द्वितीय स्तम्भ : (-1) + (-2) + 3
= – 1 – 2 + 3 = 0
तृतीय स्तम्भ : (-4) + 7 + (-3)
= – 4 + 7 – 3 = 0
पहला विकर्ण : 5 + (-2) + (-3)
= 5 – 2 – 3 = 0
परन्तु दूसरा विकर्ण : 0 + (-2) + (-4)
= 0 – 2 – 4 = – 6
∴ प्रत्येक पंक्ति, स्तम्भ तथा विकर्ण का योग समान नहीं है। अत: यह एक मायावी वर्ग नहीं है।
(ii) द्वितीय वर्ग में :
प्रथम पंक्ति : 1 + (-10) + 0
= 1 – 10 + 0 = -9
द्वितीय पंक्ति : (-4) + (-3) + (-2)
= – 4 – 3 – 2 = – 9
तृतीय पंक्ति : (-6) + 4 + (-7)
= – 6 + 4 – 7 = – 9
प्रथम स्तम्भ : 1 + (-4) + (-6)
= 1 – 4 – 6 = -9
द्वितीय स्तम्भ : (-10) + (-3) +4
= – 10 – 3 + 4 = – 9
तृतीय स्तम्भ : 0 + (-2) + (-7)
= 0 – 2 – 7 = -9
पहला विकर्ण : 1 + (-3) + (-7)
= 1 – 3 – 7 = -9
और दूसरा विकर्ण : (-6) + (-3) + 0
= – 6 – 3 + 0 = -9
∴ प्रत्येक स्तम्भ, पंक्ति तथा विकर्ण के योग समान हैं। अत: यह एक मायावी वर्ग है।
![]()
प्रश्न 8.
a और b के निम्नलिखित मानों के लिए a -(b)= a + b का सत्यापन कीजिए:
(i) a = 21, b = 18
(ii) a = 118, b = 125
(iii) a = 75, b = 84
(iv) a = 28,b = 11
हल :
(i) बायाँ भाग = a -(-b) = 21 – (-18)
= 21 + 18 = 39
दायाँ भाग = a + b = 21 + 18 = 39
∴ बायाँ भाग = दायाँ भाग
(ii) बायाँ भाग = a -(-b)= 118 – (-125)
= 118 + 125 = 243
दायाँ भाग = a + b = 118 + 125 = 243
∴ बायाँ भाग = दायाँ भाग
(iii) बायाँ भाग = a -(- b) = 75 -(-84)
= 75 + 84 = 159
दायाँ भाग = a + b = 75 + 84 = 159
∴ बायाँ भाग = दायाँ भाग
(iv) बायाँ भाग = a – (-b) = 28 – (-11)
= 28 + 11 = 39
दायाँ भाग = a + b = 28 + 11 = 39
∴ बायाँ भाग = दायाँ भाग
प्रश्न 9.
निम्नलिखित कथनों को सत्य बनाने के लिए, बॉक्स में संकेत >, < अथवा = का उपयोग कीजिए:
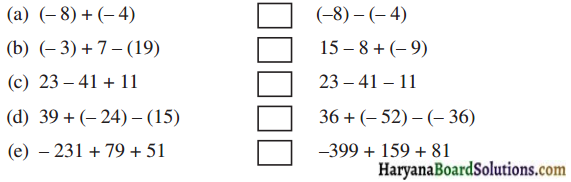
हल :
(a) यहाँ (-8) + (-4) = – 8 – 4 = – 12
और (-8) – (-4) = – 8 + 4 = – 4
चूँकि – 12 < – 4
इसलिए, (-8) + (-4) < (-8) – (-4)
(b) यहाँ (-3) + 7 – (19) = – 3 + 7 – 19
= – 22 + 7 = – 15
और 15 – 8 + (-9) = 15 – 8 – 9
= 15 – 17 = – 2
चूँकि – 15 < – 2
इसलिए, (-3) + 7 – (19)015-8+ (-9)
(c) यहाँ 23 – 41 + 11 = 34 – 41 = – 7
और 23 – 41 – 11 = 23 – 52 = – 29
चूँकि -7 > -29
इसलिए 23 – 41 + 11 > 23 – 41 – 11
(d) यहाँ 39 + (-24) – (15) = 39 – 24 – 15
= 39 -39 = 0
और 36 + (-52) – (-36) = 36 – 52 + 36
= 72 – 52 = 20
चूँकि 0 < 20
इसलिए, 39 + (-24) – (15) < 36 + (-52) – (-36)
(e) यहाँ – 231 + 79 + 51 = – 231 + 130 = -101
और – 399 + 159 + 81 = – 399 + 240 = -159
चूंकि – 101 > – 159
इसलिए, – 231 + 79 + 51 > – 399 + 159 + 81
![]()
प्रश्न 10.
पानी के एक तालाब में अन्दर की ओर सीढ़ियाँ हैं। एक बन्दर सबसे ऊपर वाली सीढ़ी (यानी पहली सीढ़ी) पर बैठा हुआ है। पानी नौवीं सीढ़ी पर है।
(i) वह एक छलाँग में तीन सीढ़ियाँ नीचे की ओर और अगली छलाँग में दो सीढ़ियों ऊपर की ओर जाता है। कितनी छलाँगों में वह पानी के स्तर तक पहुँच पाएगा?
(i) पानी पीने के पश्चात् वह वापस जाना चाहता है। इस कार्य के लिए वह एक छलाँग में 4 सीढ़ियाँ ऊपर की ओर और अगली छलाँग में 2 सीढ़ियाँ नीचे की ओर जाता है। कितनी छलाँगों में वह वापस सबसे ऊपर वाली सीढ़ी पर पहुँच जाएगा?
(iii) यदि नीचे की ओर पार की गई सीढ़ियों की संख्या को ऋणात्मक पूर्णाक से निरूपित किया जाता है और ऊपर की ओर पार की गई सीढ़ियों की संख्या को धनात्मक पूर्णांक से निरूपित किया जाता है, तो निम्नलिखित को पूरा करते हुए भाग (i) और (ii) में उसकी गति को निरूपित कीजिए :
(a) – 3 + 2 – …….. = – 8
(b) 4 – 2 + …… = 8.
(c) में योग (-8) आठ सीढ़ियों नीचे जाने को निरूपित करता है, तो (b) में योग 8 किसको निरूपित करेगा?
हल :
(i) नीचे जाते समय बन्दर एक छलांग में 3 सीढ़ियाँ नीचे कूदता है तथा अगली छलाँग में 2 वापस ऊपर की ओर।
अत: पानी तक पहुँचने के लिए वह प्रति छलाँग निम्न प्रकार कूदेगा :
– 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 = – 8
अत: पानी तक पहुँचने के लिए वह 11 बार छलांग लगायेगा।
(ii) पानी पीने के पश्चात् वह ऊपर वाली सीढ़ी तक पहुँचने के लिए प्रति छलाँग निम्न प्रकार कूदेगा :
4 – 2 + 4 – 2 + 4 = 8
अत: वह वापसी के लिए 5 बार छलांग लगायेगा।
(iii) (a) -3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 = -8
(b) 4 – 2 + 4 – 2 + 4 = 8
(b) में योग 8 का अर्थ ऊपर जाने वाली सीढ़ियों से है।