HBSE 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.2

Haryana State Board HBSE 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Exercise 13.2

प्रश्न 1.
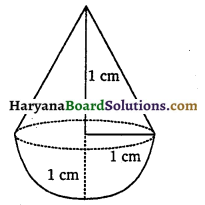
एक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 cm हैं तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है। इस ठोस का आयतन π के पदों में ज्ञात कीजिए।
हल :
यहाँ पर,
दिए गए ठोस के अर्धगोलाकार भाग की त्रिज्या (r) = 1 cm
दिए गए ठोस के शंक्वाकार भाग की त्रिज्या (r) = 1 cm
दिए गए ठोस के शंक्वाकार भाग की ऊँचाई (h) = 1 cm
अतः दिए गए ठोस का आयतन = (अर्धगोलाकार भाग + शंक्वाकार भाग) का आयतन

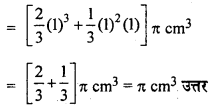
प्रश्न 2.
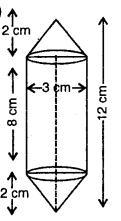
एक इंजीनियरिंग के विद्यार्थी रचेल से एक पतली एल्यूमीनियम की शीट का प्रयोग करते हुए एक मॉडल बनाने को कहा गया जो एक ऐसे बेलन के आकार का हो जिसके दोनों सिरों पर दो शंकु जुड़े हुए हों। इस मॉडल का व्यास 3 cm है और इसकी लंबाई 12 cm है। यदि प्रत्येक शंकु की ऊँचाई 2 cm हो तो रचेल द्वारा बनाए बए मॉडल में अंतर्विष्ट हवा का आयतन ज्ञात कीजिए। (यह मान लीजिए कि मॉडल की आंतरिक और बाहरी विमाएँ लगभग बराबर हैं।)
हल :

यहाँ पर,
मॉडल के बेलनाकार भाग की त्रिज्या (r₁) = \(\frac{3}{2}\) cm
k-3 cm मॉडल के बेलनाकार भाग की ऊँचाई (h₁) (12-2 x 2) cm
= 8 cm
मॉडल के प्रत्येक शंक्वाकार भाग की त्रिज्या (r₂) = \(\frac{3}{2}\) cm
मॉडल के प्रत्येक शंक्वाकार भाग की ऊँचाई (h₂) = 2 cm
मॉडल में अंतर्विष्ट हवा का आयतन = (बेलनाकार भाग + दोनों शंक्वाकार भागों) का आयतन

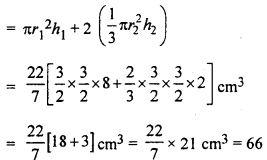
प्रश्न 3.
एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चाशनी होती है। 45 गुलाबजामुनों में लगभग कितनी चाशनी होगी, यदि प्रत्येक गुलाबजामुन एक बेलन के आकार का है, जिसके दोनों सिरे अर्धगोलाकार हैं तथा इसकी लंबाई 5 cm और व्यास 2.8 cm है (देखिए संलग्न आकृति)।
हल :


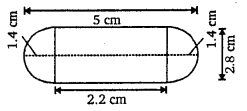
यहाँ पर,
गुलाबजामुन के बेलनाकार भाग की त्रिज्या (r₁) = \(\frac{2.8}{2}\) = 1.4 cm
गुलाबजामुन के बेलनाकार भाग की ऊँचाई (h₁) = (5 – 1.4 x 2) cm
= 2.2 cm
गुलाबजामुन के प्रत्येक अर्धगोलाकार भाग की त्रिज्या (r₂) = \(\frac{2.8}{2}\) cm = 1.4 cm अतः 1 गुलाबजामुन का आयतन = (बेलनाकार भाग + दोनों शंक्वाकार भागों) का आयतन
= πr₁²h₁ + 2(\(\frac{2}{3}\)πr₂²)
= [ \(\frac{22}{7}\) x 1.4 x 1.4 x 2.2 + \(\frac{4}{3} \times \frac{22}{7}m\) x 1.4 x 1.4 x 1.4] cm³
= [13.552 + 11.499]cm³ = 25.051 cm³
45 गुलाबजामुनों का आयतन = 45 x 25.051 cm³
= 1127.295 cm³ = 1127 cm³
अतः 45 गुलाबजामुनों में चीनी की चाशनी की मात्रा = \(\frac{1127 \times 30}{100}\) cm³
= 338.1 cm³ = 338 cm³

प्रश्न 4.
एक कलमदान घनाभ के आकार की एक लकड़ी से बना है जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढे बने हुए हैं। घनाभ की विमाएँ 15 cm x 10 cm x 3.5 cm हैं। प्रत्येक गड्ढे की त्रिज्या 0.5 cm है और गहराई 1.4 cm है। पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए (देखिए संलग्न आकृति)।
हल :

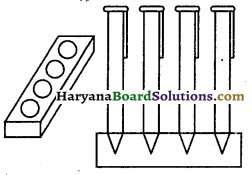
यहाँ पर,
घनाभाकार लकड़ी का कुल आयतन = (15 x 10 x 3.5) cm³
= 525 cm³
कलमदान के प्रत्येक शंक्वाकार गड्ढे की त्रिज्या (r) = 0.5 cm
कलमदान के प्रत्येक शंक्वाकार गड्ढे की गहराई (h) = 1.4 cm
कलमदान के चारों शंक्वाकार गड्ढों का आयतन = 4(\(\frac{1}{3}\) πr²h)
= \(\frac{4}{3} \times \frac{22}{7}\) x 0.5 x 0.5 x 1.4 cm³
= 1.47 cm³
अतः कलमदान की लकड़ी का आयतन = (घनाभाकार लकड़ी – शंक्वाकार गड्ढों ) का आयतन
= (525 – 1.47) cm³
= 523.53 cm

प्रश्न 5.
एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 cm है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 cm है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें प्रत्येक 0.5 cm त्रिज्या वाला एक गोला है, डाली जाती हैं, तो इसमें से भरे हुए पानी का एक चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
हल :
यहाँ पर,
शंकु के आकार के बर्तन की त्रिज्या (r₁) = 5 cm
शंकु के आकार के बर्तन की ऊँचाई (h) = 8 cm

बर्तन में डाली गई प्रत्येक सीसे की गोली की त्रिज्या (r₂) = 0.5 cm

प्रश्न 6.
ऊँचाई 220 cm और आधार व्यास 24 cm वाले एक बेलन, जिस पर ऊँचाई 60 cm और त्रिज्या 8 cm वाला एक अन्य बेलन आरोपित है, से लोहे का एक स्तंभ बना है। इस स्तंभ का द्रव्यमान ज्ञात कीजिए, जबकि दिया है 1 cm’ लोहे का द्रव्यमान लगभग 8g होता है। (π = 3.14 लीजिए।)
हल :

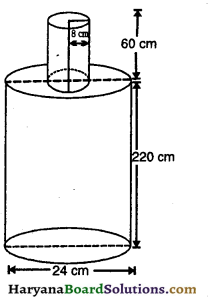
यहाँ पर,
बड़े बेलन का व्यास = 24 cm
बड़े बेलन की त्रिज्या (R) = \(\frac{24}{2}\) cm = 12 cm
बड़े बेलन की ऊँचाई (H) = 220 cm
बड़े बेलन का आयतन (V₁) = πR²H
= 3.14 x 12 x 12 x 220 cm³
= 99475.2 cm²
छोटे बेलन की त्रिज्या (r) = 8 cm
छोटे बेलन की ऊँचाई (h) = 60 cm
छोटे बेलन का आयतन (V₂) = πr²h
= 3.14 x 8×8 x 60 cms
= 12057.6 cm स्तंभ में लगे कुल लोहे का आयतन = V₁ + V₂
= (99475.2 + 12057.6) cm³
= 111532.8 cm³
1 cm³ लोहे का द्रव्यमान = 8g
111532.8 cm लोहे का द्रव्यमान = 111532.8 x 8 g
= [laex]\frac{111532.8 \times 8}{1000}[/latex] kg
= 892.26 kg

प्रश्न 7.
एक ठोस में, ऊँचाई 120 cm और त्रिज्या 60 cm वाला एक शंकु सम्मिलित है, जो 60 cm त्रिज्या वाले एक अर्धगोले पर आरोपित है। इस ठोस को पानी से भरे हुए एक लंब वृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि यह बेलन की तली को स्पर्श करे। यदि बेलन की त्रिज्या 60 cm है और ऊँचाई 180 cm है तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए।
हल :

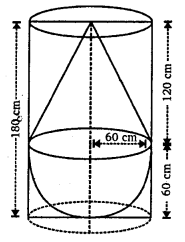
यहाँ पर,
लंब वृत्तीय बेलनाकार बर्तन की त्रिज्या (R) = 60 cm
लंब वृत्तीय बेलनाकार बर्तन की ऊँचाई (H) = 180 cm
लंब वृत्तीय बेलनाकार बर्तन का आयतन (V₁) = πR²H
= \(\frac{22}{7}\) x 60 x 60 x 180cm³
= 2036571.40 cm³
ठोस के शंक्वाकार भाग की त्रिज्या (r) = अर्धगोलाकार भाग की त्रिज्या
(r) = 60 cm
ठोस के शंक्वाकार भाग की ऊँचाई (h) = 120 cm
ठोस का आयतन (V₂) = (शंक्वाकार भाग + अर्धगोलाकार भाग) का आयतन

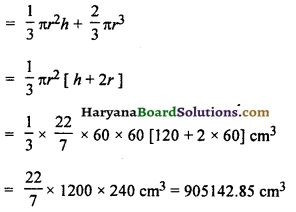
अतः बेलनाकार बर्तन में शेष बचे पानी का आयतन = V₁ – V₂
= (2036571.40-905142.85) cm³
= 1131428.55 cm³
= 1.131m³ (लगभग)

प्रश्न 8.
एक गोलाकार काँच के बर्तन की एक बेलन के आकार की गर्दन है जिसकी लंबाई 8 cm है और व्यास 2 cm है जबकि गोलाकार भाग का व्यास 8.5 cm है। इसमें भरे जा सकने वाली पानी की मात्रा माप कर, एक बच्चे ने यह ज्ञात किया कि इस बर्तन का आयतन 345 cm है। जाँच कीजिए कि उस बच्चे का उत्तर सही है या नहीं, यह मानते हुए कि उपरोक्त मापन आंतरिक मापन है और π = 3.14
हल :
यहाँ पर,
बर्तन के बेलनाकार भाग का व्यास (d₁) = 2 cm
बर्तन के बेलनाकार भाग की त्रिज्या (r₁) = \(\frac{2}{2}\) cm = 1 cm
बर्तन के बेलनाकार भाग की ऊँचाई (h) = 8 cm
बर्तन के बेलनाकार भाग का आयतन (V₁) = πr₁²h
= 3.14 x 1 x 1 x 8 cm³
= 25.12 cm
बर्तन के गोलाकार भाग का व्यास (d₂) = 8.5 cm
बर्तन के गोलाकार भाग की त्रिज्या (r₂) = \(\frac{8.5}{2}\) cm = 4.25 cm
बर्तन के गोलाकार भाग का आयतन (V₂) = \(\frac{4}{3} \pi r_{2}^{3}\)
= \(\frac{4}{3}\) x 3.14 x 4.25 x 4.25 x 4.25 cm³
= 321.39 cm ³
बर्तन में भरे जा सकने वाले पानी का कुल आयतन = V₁ + V₂
= [25.12 + 321.39] cm³
= 346.51 cm³
अतः बच्चे का उत्तर 345 cm³ सही नहीं है।