HBSE 10th Class Maths Solutions Chapter 12 वृत्तों से संबंधित क्षेत्रफल Ex 12.3

Haryana State Board HBSE 10th Class Maths Solutions Chapter 12 वृत्तों से संबंधित क्षेत्रफल Ex 12.3 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 12 वृत्तों से संबंधित क्षेत्रफल Exercise 12.3

प्रश्न 1.
संलग्न आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि .. PQ = 24cm, PR = 7cm तथा 0 वृत्त का केंद्र है।
हल :

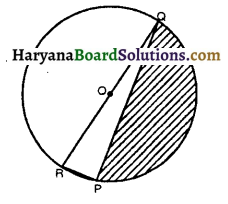
यहाँ पर,
PQ = 24cm
PR = 7cm
हम जानते हैं कि अर्धवृत्त में बना कोण ∠RPQ = 90°
समकोण त्रिभुज RPQ में पाइथागोरस प्रमेय से

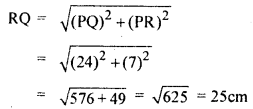
अतः दिए गए वृत्त का व्यास (RQ) = 25cm
दिए गए वृत्त की त्रिज्या (r) = \(\frac{25}{2}\) cm
दिए गए वृत्त के छायांकित भाग का क्षेत्रफल = अर्धवृत्त का क्षेत्रफल – ΔRPQ का क्षेत्रफल

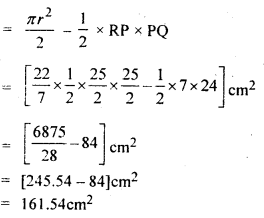
प्रश्न 2.
संलग्न आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र 0 वाले दोनों संकेंद्रीय वृत्तों की त्रिज्याएँ क्रमशः 7cm और 14cm हैं तथा ∠AOC = 40° है।
हल :

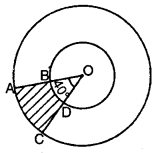
यहाँ पर, बड़े वृत्त की त्रिज्या (R) = 14cm
छोटे वृत्त की त्रिज्या (r) = 7cm
चाप AC तथा चाप BD द्वारा केंद्र पर अंतरित कोण (e) = 40°
छायांकित त्रिज्यखंड का क्षेत्रफल = (त्रिज्यखंड AOC – त्रिज्यखंड BOD) का क्षेत्रफल

प्रश्न 3.
संलग्न आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14cm का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं।
हल :

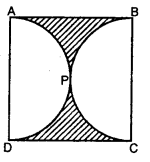
यहाँ पर, वर्ग ABCD की भुजा = 14cm
वर्ग ABCD का क्षेत्रफल = भुजा – भुजा
= 14 x 14 cm² = 196 cm²
प्रत्येक अर्धवृत्त की त्रिज्या (r) = \(\frac{14}{2}\) = 7 cm
दोनों अर्धवृत्तों (APD + BPC) का क्षेत्रफल = 2 x (\(\frac{1}{2}\) πr² )
= \(\frac{22}{7}\) x 7 x 7 cm²
= 154 cm²
अतः आकृति के छायांकित भाग का क्षेत्रफल = (196 – 154) cm²
= 42 cm²

प्रश्न 4.
संलग्न आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ भुजा 12cm वाले एक समबाहु त्रिभुज OAB के शीर्ष 0 को केंद्र मानकर 6 सें०मी० त्रिज्या वाला एक वृत्तीय चाप खींचा गया है।
हल :

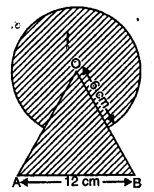
यहाँ पर, ΔAOB समबाहु त्रिभुज है। .
∴ ∠AOB = 60°
[∵ समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।]
समबाहु ΔOAB का क्षेत्रफल = \(\frac{\sqrt{3}}{4}\) – (भुजा)²
= \(\frac{\sqrt{3}}{4}\) x 12 x 12 cm²
= 36√3 cm²
वृत्त की त्रिज्या (r) = 6cm
वृत्त का क्षेत्रफल = πr²
= \(\frac{22}{7}\) x 6 x 6 cm²
= \(\frac{792}{7}\) cm²

प्रश्न 5.
भुजा 4 cm वाले एक वर्ग के प्रत्येक कोने से 1 cm त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है तथा बीच में 2 cm व्यास का एक वृत्त भी काटा गया है, जैसाकि संलग्न आकृति में दर्शाया गया है। वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
हल :

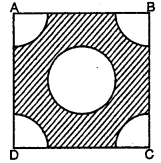
यहाँ पर,
दिए गए वर्ग की भुजा = 4 cm
दिए गए वर्ग का क्षेत्रफल = भुजा – भुजा
= 4 x 4 cm² = 16 cm²
कोने से काटे गए वृत्त के प्रत्येक चतुर्थांश की त्रिज्या (r₁) = 1 cm
कोने से काटे गए वृत्त के चारों चतुर्थांश का क्षेत्रफल = 4 x प्रत्येक चतुर्थांश का क्षेत्रफल
= \(4\left(\frac{\pi r_{1}^{2}}{4}\right)=\frac{22}{7}\) = x 1 x 1 cm²
= \(\frac{22}{7}\)cm²
बीच के वृत्त का व्यास = 2 cm
बीच के वृत्त की त्रिज्या (r₂) = 2/2 cm = 1 cm

प्रश्न 6.
एक वृत्ताकार मेज़पोश, जिसकी त्रिज्या 32 cm है, में बीच में एक समबाहु त्रिभुज ABC छोड़ते हुए एक डिज़ाइन बना हुआ है, जैसाकि संलग्न आकृति में दिखाया गया है। इस छायांकित डिज़ाइन का क्षेत्रफल ज्ञात कीजिए।

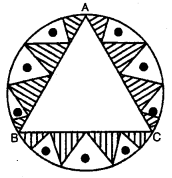
हल :

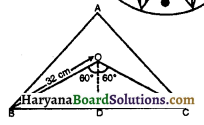
यहाँ पर, समबाहु त्रिभुज ABC की भुजा BC द्वारा वृत्त के केंद्र O पर
अंतरित कोण (BOC) = \(\frac{360^{\circ}}{3}\) = 120°
ΔBOD में,
∠BOD = \(\frac{120^{\circ}}{2}\) = 60° ; OB (वृत्त की त्रिज्या) = 32cm
\(\frac{\mathrm{OD}}{\mathrm{OB}}\)= cos 60° तथा \(\frac{\mathrm{BD}}{\mathrm{OB}}\) = sin 60°
\(\frac{\mathrm{OD}}{32}=\frac{1}{2}\) तथा \(\frac{\mathrm{BD}}{32}=\frac{\sqrt{3}}{2}\)
समबाहु त्रिभुज ABC की भुजा BC = 2 x BD = 2 x 16√3 cm
= 32√3 cm
दिए गए वृत्त का क्षेत्रफल = πr²

अतः दी आकृति के छायांकित भाग का क्षेत्रफल = \(\left[\frac{22528}{7}-768 \sqrt{3}\right]\) cm²

प्रश्न 7.
संलग्न आकृति में, ABCD भुजा 14 cm वाला एक वर्ग है। A,B,C और D को केंद्र मानकर, चार वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त तीन शेष वृत्तों में से दो वृत्तों को बाह्य रूप से स्पर्श करता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल :

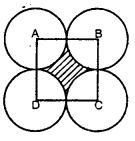
यहाँ पर,
दिए गए वर्ग ABCD की भुजा = 14 cm
दिए गए वर्ग ABCD का क्षे० = भुजा – भुजा
= (14 x 14)cm2 = 196cm2
प्रत्येक वृत्त के चतुर्थांश की त्रिज्या (r) = \(\frac{14}{2}\) = 7 cm
प्रत्येक वृत्त के चतुर्थांश का क्षेत्रफल = \(\frac{\pi r^{2}}{4}=\frac{22}{7} \times \frac{7 \times 7}{4}\) cm²
= \(\frac{77}{2}\) cm²
चारों वृत्तों के चारों चतुर्थांशों का क्षेत्रफल = 4 x प्रत्येक चतुर्थांश का क्षेत्रफल .
= 4 x \(\frac{77}{2}\) cm² = 154 cm²
अतः आकृति के छायांकित भाग का क्षेत्रफल = वर्ग का क्षेत्रफल – चार चतुर्थांशों का क्षेत्रफल
= (196 – 154) cm²
= 42 cm²

प्रश्न 8.
संलग्न आकृति एक दौड़ने का पथ (racing track) दर्शाती है, जिसके बाएँ और दाएँ सिरे अर्धवृत्ताकार हैं।

दोनों आंतरिक समांतर रेखाखंडों के बीच की दूरी 60m है तथा इनमें से प्रत्येक रेखाखंड 106m लंबा है। यदि यह पथ 10m चौड़ा है, तो ज्ञात कीजिए।
(i) पथ के आंतरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दूरी
(ii) पथ का क्षेत्रफल।
हल :
यहाँ पर,

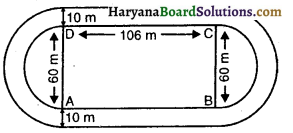
(i) प्रत्येक आंतरिक अर्धवृत्त का व्यास = 60m
प्रत्येक आंतरिक अर्धवृत्त की त्रिज्या (r) = \(\frac{60}{2}\) = 30 m
दोनों आंतरिक अर्धवृत्तों की परिधि = 2 x प्रत्येक अर्धवृत्त की परिधि
= 2 x (πr)
= 2 x \(\frac{22}{7}\) x 30m
= \(\frac{1320}{7}\) m
= Sm आंतरिक दोनों किनारों की दूरी = AB + CD = (106 + 106)m
= 212 m
अतः पथ के आंतरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में तय दूरी

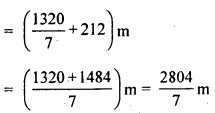
(ii) आंतरिक आयत का क्षेत्रफल = 106 x 60 m² = 6360 m²
बाहरी आयत का क्षेत्रफल = 106 x 80 m² = 8480 m²
आयताकार छायांकित आकृति का क्षेत्रफल = बाहरी क्षेत्रफल – आंतरिक क्षेत्रफल
= (8480 – 6360)m² = 2120m²
प्रत्येक बाहरी अर्धवृत्त की त्रिज्या (R) = 80/2 = 40m
प्रत्येक अर्धवृत्ताकार छायांकित आकृति का क्षेत्रफल= \(\frac{1}{2}\)[πR² – πr²]
= \(\frac{1}{2} \times \frac{22}{7}\) [(40)² – (30)²] cm = ” x 700 m² = 1100 m²
वृत्तों से संबंधित क्षेत्रफल दोनों अर्धवृत्ताकार छायांकित आकृतियों का क्षेत्रफल = 2 x 1100 m²
= 2200 m²
अतः छायांकित कुल पथ का क्षेत्रफल = (2120 + 2200) m²
= 4320 m²

प्रश्न 9.
संलग्न आकृति में, AB और CD केंद्र 0 वाले एक वृत्त के दो परस्पर लंब व्यास हैं तथा OD छोटे वृत्त का व्यास है। यदि OA = 7cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल :

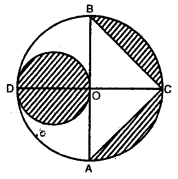
यहाँ पर,
बड़े वृत्त की त्रिज्या (OA) = 7cm
बड़े वृत्त का व्यास (AB) = 2 x OA = 2 x 7cm = 14cm
परंतु OC = OA = 7cm (प्रत्येक बड़े वृत्त की त्रिज्या)
ΔABC का क्षेत्रफल = \(\frac{1}{2}\) x AB x OC
= \(\frac{1}{2}\) x 14 x 7 cm² = 49cm²
बड़े अर्धवृत्त का क्षेत्रफल = T(OA) = \(\frac{\pi(\mathrm{OA})^{2}}{2}=\frac{22}{7} \times \frac{1}{2}\)x 7 x 7 cm2
= 77 cm²
दिए गए छोटे वृत्त का व्यास (OD) = 7cm (बड़े वृत्त की त्रिज्या)
दिए गए छोटे वृत्त की त्रिज्या (r) = \(\frac{7}{2}\) cm
दिए गए छोटे वृत्त का क्षेत्रफल =πr²= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)cm² = 38.5cm²
अतः छायांकित भाग का क्षेत्रफल = छोटे वृत्त का क्षेत्रफल + (बड़े अर्धवृत्त का क्षेत्रफल – AABC का क्षेत्रफल)
= [38.5 + (77-49)] cm²
= [38.5 + 28] cm²
= 66.5 cm²

प्रश्न 10.
एक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 cm है। इस त्रिभुज के प्रत्येक शीर्ष को केंद्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है (देखिए संलग्न आकृति)। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
(π = 3.14 और √3 = 1.73205 लीजिए।)
हल :

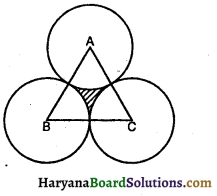
यहाँ पर, समबाहु त्रिभुज ABC का क्षेत्रफल = 17320.5 cm²
\(\frac{\sqrt{3}}{4}\) (भुजा)² = 17320.5 cm
(भुजा)² = 17320.5 x \(\frac{4}{\sqrt{3}}\)
= \(\frac{17320.5 \times 4}{1.73205}\) = 40000
= (200)²
भुजा = 200 cm
प्रत्येक वृत्त की त्रिज्या (r) =
= 100 cm
प्रत्येक त्रिज्यखंड का कोण (θ) = 60० (समबाहु त्रिभुज का प्रत्येक कोण)
तीनों त्रिज्यखंडों का क्षेत्रफल = \(3\left[\frac{\theta}{360} \times \pi r^{2}\right]\)
= 3 x \(\frac{60}{360}\) x 3.14 x 100 x 100ccm²
= 15700 cm²
इस प्रकार, आकृति के छायांकित भाग का क्षेत्रफल = ΔABC का क्षेत्रफल – तीनों त्रिज्यखंडों का क्षेत्रफल
= (17320.5-15700)cm²
= 1620.5cm²

प्रश्न 11.
एक वर्गाकार रूमाल पर, नौ वृत्ताकार डिज़ाइन बने हैं, जिनमें से प्रत्येक की। त्रिज्या 7cm है (देखिए संलग्न आकृति)। रूमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
हल :

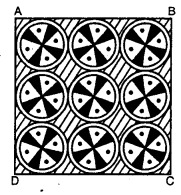
यहाँ पर,
रूमाल के प्रत्येक वृत्ताकार डिजाइन की त्रिज्या (r) = 7 cm
रूमाल के प्रत्येक वृत्ताकार डिजाइन का व्यास (d) = 2 x r cm
= 2×7 cm
= 14 cm
वर्गाकार रूमाल की प्रत्येक भुजा = 3 x प्रत्येक वृत्त का व्यास
= 3 x 14 cm = 42 cm
रूमाल के 9 वृत्ताकार डिजाइनों का क्षेत्रफल = 9 x πr²
= 9 x \(\frac{22}{7}\) x 7 x 7 cm²
= 1386 cm²
वर्गाकार रूमाल का क्षेत्रफल = भुजा – भुजा
= 42 x 42 cm² = 1764 cm²
अतः . वृत्ताकार डिजाइनों को छोड़कर शेष रूमाल का क्षेत्रफल = (1764 – 1386) cm2
= 378 cm²

प्रश्न 12.
संलग्न आकृति में, OACB केंद्र 0 और त्रिज्या 3.5 cm वाले एक वृत्त का चतुर्थांश है। यदि OD = 2cm है, तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए-
(i) चतुर्थांश OACB (ii) छायांकित भाग
हल :

(i) यहाँ पर, चतुर्थांश OACB की त्रिज्या (r) = 3.5 cm
चतुर्थांश OACB का क्षेत्रफल = \(\frac{\pi r^{2}}{4}\)
= \(\frac{22}{7} \times \frac{1}{4}\) x 3.5 x 3.5 cm²
= 9.625 cm²

(ii) अब समकोण AOBD का क्षेत्रफल = \(\frac{1}{2}\) x OB x OD
= \(\frac{1}{2}\) x 3.5 x 2 cm²
= 3.5 cm²
अतः आकृति के छायांकित भाग का क्षेत्रफल = (चतुर्थांश OACB — AOBD) का क्षेत्रफल
= (9.625 -3.5) cm²
= 6.125 cm²

प्रश्न 13.
संलग्न आकृति में, एक चतुर्थांश OPBQ के अंतर्गत एक वर्ग OABC बना हुआ . है। यदि OA = 20 cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल :

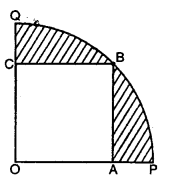
यहाँ पर, वर्ग OABC में, भुजा OA = भुजा AB = 20 cm
वर्ग OABC का क्षेत्रफल = भुजा x भुजा
= 20 x 20 cm² = 400 cm²

= 628 cm²
अतः आकृति के छायांकित भाग का क्षेत्रफल = (चतुर्थांश OPBQ – वर्ग OABC) का क्षेत्रफल
= (628 – 400) cm²
= 228 cm²

प्रश्न 14.
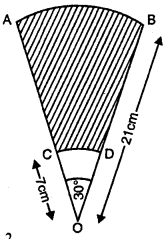
AB और CD केंद्र O तथा त्रिज्याओं 21cm और 7cm वाले दो संकेंद्रीय वृत्तों के क्रमशः दो चाप हैं (देखिए संलग्न आकृति)। यदि ∠AOB = 30° है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल :

यहाँ पर,
त्रिज्यखंड OAB की त्रिज्या (R) = 21 cm
चाप AB द्वारा केंद्र O पर अंतरित कोण (θ) = 30°
त्रिज्यखंड OAB का क्षेत्रफल = \(\frac{\theta}{360}\) x πR²
= \(\frac{30}{360} \times \frac{22}{7}\) x 21 x 21 cm²
= \(\frac{231}{2}\) cm²
त्रिज्यखंड OCD की त्रिज्या (r) = 7 cm
चाप CD द्वारा केंद्र O पर अंतरित कोण (θ) = 30°
त्रिज्यखंड OCD का क्षेत्रफल = \(\frac{\theta}{360}\) x πr²
= \(\frac{30}{360} \times \frac{22}{7}\) x 7 x 7 cm²
= \(\frac{77}{6}\) cm²
अतः आकृति के छायांकित भाग का क्षेत्रफल = (त्रिज्यखंड OAB — त्रिज्यखंड OCD) का क्षेत्रफल

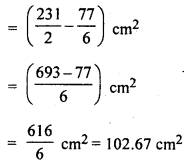
प्रश्न 15.
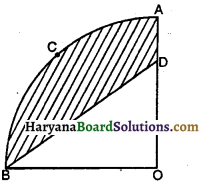
संलग्न आकृति में, ABC त्रिज्या 14 cm वाले एक वृत्त का चतुर्थांश है तथा BC को व्यास मान कर एक अर्धवृत्त खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल :

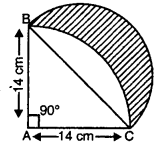
यहाँ पर, समकोण त्रिभुज ABC में, AB = AC = 14 cm
(वृत्त की त्रिज्या के समान)

समकोण त्रिभुज ABC का क्षेत्रफल = \(\frac{1}{2}\) x AC x AB
= \(\frac{1}{2}\) x 14 x 14 cm² = 98 cm²
अतः आकृति में दर्शाए गए छायांकित. भाग का क्षेत्रफल
= BC पर बने अर्धवृत्त का क्षेत्रफल – (चतुर्थांश का क्षेत्रफल – ΔABC का क्षेत्रफल)
= [154 -(154-98)] cm²
= [154 – 154 + 98] cm² = 98 cm²

प्रश्न 16.
संलग्न आकृति में, छायांकित डिज़ाइन का क्षेत्रफल ज्ञात कीजिए, जो 8cm त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है।
हल :

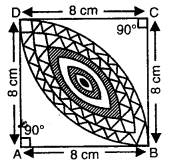
यहाँ पर,
आकृति में छायांकित डिजाइन का क्षेत्रफल = 2[चतुर्थांश ABD का क्षेत्रफल – समकोण ΔABD का क्षेत्रफल)