HBSE 10th Class Maths Solutions Chapter 11 Constructions Ex 11.1

Haryana State Board HBSE 10th Class Maths Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 11 Constructions Ex 11.1

In each of the following, give the justification of the construction also:

Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution:
Steps of Construction :
1. Draw a line segment AB = 7.6 cm.
2. Draw any ray AX, making an acute angle with AB.
3. Along AX mark (5 + 8) = 13 points A₁, A₂,
A₃ ……………………. A₁₃ such that AA₁ = A₁A₂ = A₂A₃ = …………………….. A₁₂A₁₃

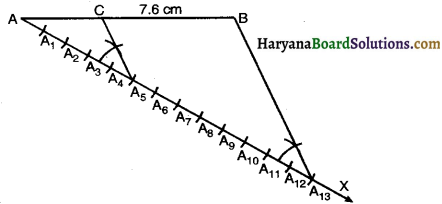
4. Join A₁₃B.
5. Through A₅, draw A₅C || A₁₃B meeting AB at C.
6. Then AC : BC = 5 : 8.
7. On measuring
AC = 2.9 cm
CB = 4.7 cm
Justification : In ∆ABA₁₃, A₅C || A₁₃B.
\(\frac{\mathrm{AA}_5}{\mathrm{~A}_5 \mathrm{~A}_{13}}=\frac{\mathrm{AC}}{\mathrm{BC}}\) [By Basic proportionality theorem]
But \(\frac{\mathrm{AA}_5}{\mathbf{A}_5 \mathbf{A}_{13}}=\frac{5}{8}\) [By construction]
∴ \(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{5}{8}\)
AC : BC = 5 : 8.

Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac{2}{3}\) of the coi responding sides of the first triangle.
Solution:
Steps of construction :
1. Draw a line segment BC = 5 cm.
2. With B as a centre and radius 4 cm draw an arc.
3. With C as a centre and radius 6 cm draw another arc to intersect the first arc. at A.

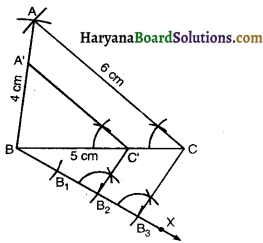
4. Join BA and CA to get ∆ABC.
5. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
6. Along BX mark 3 points B₁, B₂ and B₃ such that BB₁ = B₁B₂ = B₂B₃.
7. Join B₃C.
8. From B₂ draw B₂C’ || B₃C meeting BC at C’.
9. From C’ draw C’A’ || CA meeting BA at A’.
Then A’BC’ is the required triangle, each of whose side is \(\frac{2}{3}\) of corresponding Sides of ∆ABC.
Justification : Since, A’C’ || AC
Therefore, ∆A’BC’ ~ ∆ABC
\(\frac{\mathrm{AB}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{2}{3}\)

Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle 7 whose sides are \(\frac{7}{5}\) of the corresponding sides of the 5 first triangle.
Solution:
Steps of Construction :
1. Draw a line segment BC = 6 cm.
2. With B as a centre and radius 5 cm draw an arc.
3. With C as a centre and radius 7 cm draw another arc to intersect the first arc at A.
4. Join BA and CA to get ∆ABC.

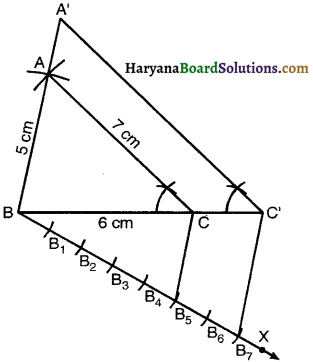
5. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
6. Along BX mark 7 points B₁, B₂, B₃, …….., B₇ such that BB₁ = B₁B₂ = B₂B₃ = ………….. = B₆B₇.
7. Join B₅C.
8. From B₇ draw B₇C’ || B₅₆C intersecting the produced line segment BC at C’.
9. From C’ draw CA’ || AC intersecting the produced line segment BA at A’.
Then, ∆A’BC’ is the required triangle each of whose side is \(\frac{7}{5}\) of the corresponding sides of the ∆ABC.
Justification : Since, AC || A’C’
Therefore, ∆A’BC’ ~ ∆ABC
⇒ \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{7}{5}\)

Question 4.
Construct an Isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of the isosceles triangle.
Solution:
Steps of Construction :
1. Let ABC be the isosceles triangle with base AB = 8 cm and altitude CD = 4 cm.
2. Draw a line segment AB = 8 cm.
3. Draw the perpendicular bisector of AB intersecting AB at D.
4. With D as a centre and radius 4 cm draw an arc intersecting the perpendicular bisector at C.
5. Join AC and BC to get the isosceles triangle ABC.

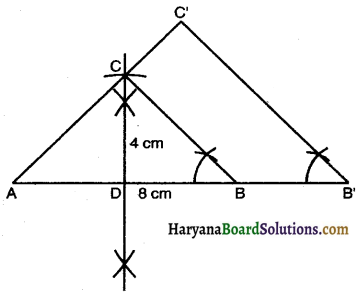
6. Produce AB to B’ AB’ = 1\(\frac{1}{2}\) of 8 = \(\frac{3}{2}\) × 8 = 12 cm.
7. Through B’ draw B’C’ || BC intersecting the produced line segment AC to C’.
Then AB’C’ is the required triangle each of whose side is 1\(\frac{1}{2}\) times of the corresponding sides of ∆ABC.
Justification : Since, BC || B’C’
Therefore, ∆C’AB’ ~ ∆CAB
⇒ \(\frac{\mathrm{AC}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}=\frac{3}{2}\).

Question 5.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are \(\frac{3}{4}\) of the corresponding sides of the triangle ABC.
Solution:
Steps of Construction:
1. Draw a line segment BC = 6 cm.
2. At B, draw ∠CBY = 60°.
3. From B draw an arc AB = 5 cm meeting BY at A. Join AC. Thus ∆ABC obtained.
4. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
5. Along BX mark four points B₁, B₂, B₃, B₄ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
6. Join B₄C.

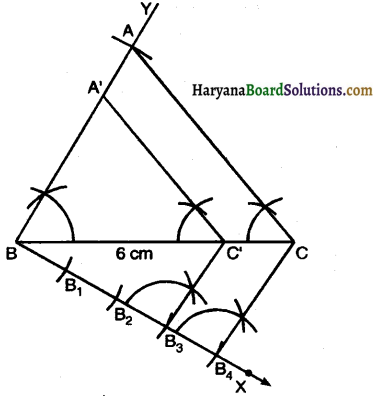
7. From B₃ draw B₃C’ || B₄C meeting BC at C.
8. From C’ draw C’A’ || CA, meeting AB at A’. Then A’BC’ is the required triangle, each of whose side is \(\frac{3}{4}\) of corresponding sides of AABC.
Justification: Since, A’C || AC
Therefore, ∆A’BC ~ ∆ABC
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{3}{4}\).

Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are \(\frac{4}{3}\) times the corresponding sides of ∆ABC.
Solution:
Steps of Construction :
1. Draw line segment BC = 7 cm.
In ∆ABC, ∠B = 45°, ∠A = 105°,
∠C = 180° – (45° + 105°) = 30°
2. At B draw an angle ∠B = 45° and at C draw an angle ∠C *= 30° intersecting each other at A to get ∆ABC.
3. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
Along BX mark four points B₁, B₂, B₃ and B₄ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.

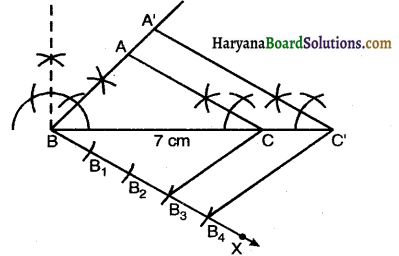
4. Join B₃C.
5. From B₄ draw B₄C’ || B₃C intersecting the produced line segment BC at C’.
6. From C’ draw C’A’ || CA intersecting the produced line segment BA at A’.
Then A’BC’ is the required triangle, each of whose side is \(\frac{4}{3}\) times the corresponding sides of ∆ABC.
Justification : Since, AC || A’C’
Therefore, ∆A’BC’ ~ ∆ABC
\(\frac{\mathrm{AB}^{\mathrm{B}}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{4}{3}\).

Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of the given triangle.
Solution:
Steps of Construction :
1. Let ABC be right triangle in which ∠B = 90°, BC = 4 cm and AB = 3 cm.
2. Draw BC = 4 cm
3. Draw ∠CBY = 90° at B.
4. Cut AB = 3 cm from BY. Join AC to get ∆ABC.
5. Draw any ray CX making an acute angle with BC on the side opposite to the vertex A.
6. Along CX mark five points C₁, C₂, C₃, C₄ and C₅ such that CC₁ = C₁C₂ = C₂C₃ = C₃C₄ = C₄C₄₅.
Join C₃B.

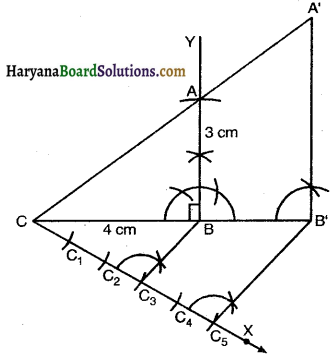
7. From C₅ draw C₅B’ || C₃B intersecting the produced line segment CB at B’.
8. From B’ draw B’A’ || BA intersecting the produced line segment CA at A’.
Then, A’CB’ is the required triangle.
Justification : Since, BA || B’A’
Therefore, ∆A’CB’ ~ ∆ACB
\(\frac{\mathrm{A}^{\prime} \mathrm{C}}{\mathrm{AC}}=\frac{\mathrm{B}^{\prime} \mathrm{C}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{5}{3}\).