HBSE 10th Class Maths Important Questions Chapter 9 Some Applications of Trigonometry

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 9 Some Applications of Trigonometry Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 9 Some Applications of Trigonometry

Short/Long Answer Type Questions

Question 1.
From a point on a bridge across a river the angles depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 4m from the banks. Find the width of river.
Solution :
Let A and B represent points on the bank on opposite sides of the river so that AB is the width of river. Pis a on the bridg at a height of 4 m is DP = 4m. We are required to determine the width of the river, which is the length of side AB of ΔAPB
∴ AB = AD + BD

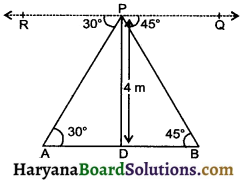
Angles of depression of the banks on opposite sides of the river are
⇒ ∠APR = 30°
⇒ ∠PAD = 30°
[alternate interior angles]
and ∠BPQ = 45°
∠PBD = 45°
In right triangle APD, we have
tan 30° = \(\frac {PD}{AD}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac {4}{AD}\)
⇒ AD = 4\(\sqrt{3}\) …………..(1)
In right triangle BPD, we have
tan 45° = \(\frac {PD}{BD}\)
⇒ 1 = \(\frac {4}{BD}\)
⇒ BD = 4 ………….(2)
Adding equ. (1) and (2), we get
AD + BD = 4\(\sqrt{3}\) + 4
= 4 × 1.732 + 4
⇒ AB = 6.928 + 4 = 10.928 m
Hence, width of river = 10.928 m.

Question 2.
As observed from the top of a 100 m high lighthouse from the sea level, the angles of depression of two ships are 30 and 45°. If one ship is exactly behind the other on same side of lighthouse, find the distance between two ships.
Solution :
Let the AB be the lighthouse of height of 100 m. Let D and C be position of two ships. The angle of depression of two ships are 30° and 45°

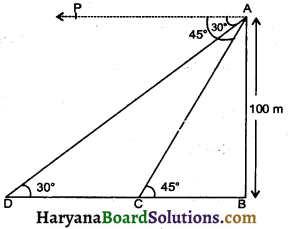
⇒ ∠DAP = 30°
⇒ ∠ADB = 30°
[Alternate interior angles]
and ∠CAP = 45°
⇒ ∠ACB = 45°
In right triangle ADB, we have
tan 30° = \(\frac {AB}{BD}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac {100}{BD}\)
⇒ BD = 100\(\sqrt{3}\)
⇒ 10 × 1.732 = 173.2 m
In right triangle ACB, we have
tan 45° = \(\frac {AB}{BC}\)
⇒ 1 = \(\frac {100}{BC}\)
⇒ BC = 100 m
⇒ DC = BD – BC
173.2 – 100 = 73.2 m
Hence distance between two ships
= DC = 73.2 m

Question 3.
The angle of elevation of the top of a hill from the foot of a tower is 60° and the angle of depression from the top of the tower of the foot of the hill is 30°. If tower is 50 m high, find the height of hill.
Solution :
Let AB be the hill of height hm and CD be the tower of height 50 m.

Angle of elevation of the top of a hill from the foot of a tower is 60° i.e. ∠ACB = 60° and angle of depression from top of the tower of the foot of the hill is 30 i.e. ∠BDE = 30°.
⇒ ∠DBC = 30°
[Alternate interior angles]
In right triangle BCD, we have
tan 30° = \(\frac {CD}{BC}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac {50}{BC}\)
⇒ BC = 50\(\sqrt{3}\) ……..(1)
In right triangle ABC, we have
tan 60° = \(\frac {AB}{BC}\)
⇒ \(\sqrt{3}\) = \(\frac {h}{BC}\)
⇒ h = \(\sqrt{3}\)BC ………..(2)
substituting, the value of BC in equ. (2), we get
h = \(\sqrt{3}\) × 50\(\sqrt{3}\)
= 50 × 3 = 150 m
Hence height of hill = 150 m

Question 4.
A vertical tower stands on a horizontal plane and is sur mounted by a vertical flag staff of height 6 m. At a point on the plane, the angle of elevation of the bottom and top of the flag staff are 30° and 45° respectvely. Find the height of the tower. Take \(\sqrt{3}\) = 1.73]
Solution :
Let AB be tower of height h m and BC be vertical flag staff of height 6m. At point D on the plane angle of elevation of the bottom and top of the flag staff are 30° and 45° respectively i.e. ∠ADB = 30° and ∠ADC = 45°
In right triangle ABD, we have

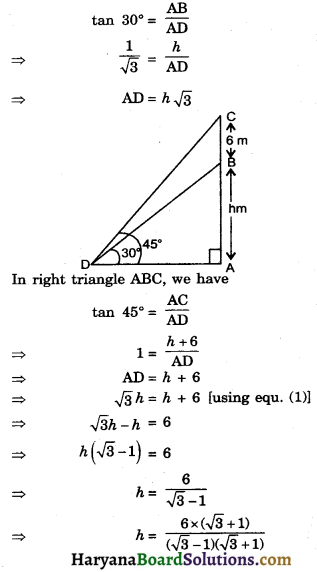
⇒ h = \(\frac{6 \times(1.73+1)}{(\sqrt{3})^2-(1)^2}\)
⇒ h = \(\frac{6 \times 2.73}{3-1}\)
⇒ h = \(\frac{6 \times 2.73}{2}\)
⇒ h = 3 × 2.73
⇒ h = 8.19 m
Hence, height of the tower h = 8.19 m

Question 5.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 48 meters high. Find the height of the building.
Solution :
Let AB be tower of the height 48 m and CD be building of height h m. Angle of elevation of the top of a building from the foot of the tower is 30° Le. ∠CBD = 30° and angle of elevation of top of the tower from the foot of the building is 60° L.E. ∠ACB = 60°,

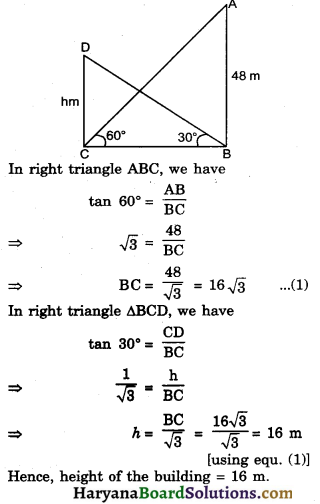
Question 6.
An aeroplane when flying at a height of 4000 m. from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of two planes from the same point on the ground are 60° and 45° repectively. Find the vertical distance between the aeroplanes at that instant.
Solution :
Let A and B be position of two aeroplanes. When A be the vertical above B and AC = 4000 m.
Let the angles of elevation of two nlanes from the point A be 60 and 45° respectively i.e. ∠ADC = 60° and ∠BDC = 45°

Hence, vertical distance between two aeroplanes = 1690.53 m.

Question 7.
Two men on either side of the cliff 80 m high observes the angles of the elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
Solution :
Let the CD be cliff of height 80 m. Let A abd B be position of eyes of two men. The angles of elevation of eyes of two men from top of the cliff be 30° and 60° respectively i.e. ∠CAD = 30° and ∠CBD = 60°.

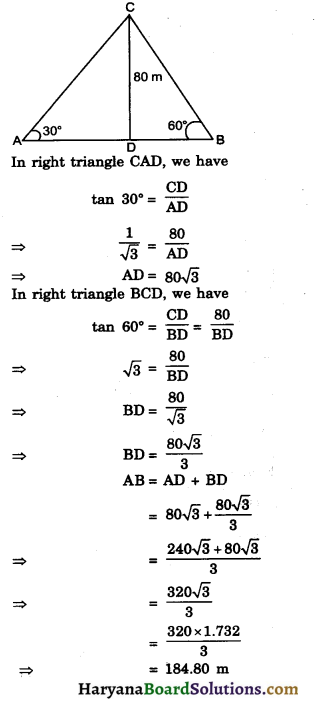
Hence, distance between two men = 184.80 m

Question 8.
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30°. The angle of depression of the reflection of the cloud in lake, at A is 60°. Find the distance of cloud from A.
Solution :
Let BR be surface of lake and A be point of observation P be position of cloud and C be the position of reflection of cloud in the lake. Draw AQ ⊥ PR. Angle of elevation of cloud from point A is 30° i.e. ∠PAQ = 30° and angle of depression of reflection of cloud in the lake is 60° i.e. ∠CAQ = 60°
Let PQ be h m, then PR = (h + 20) m and
RC = PR = (h + 20) m

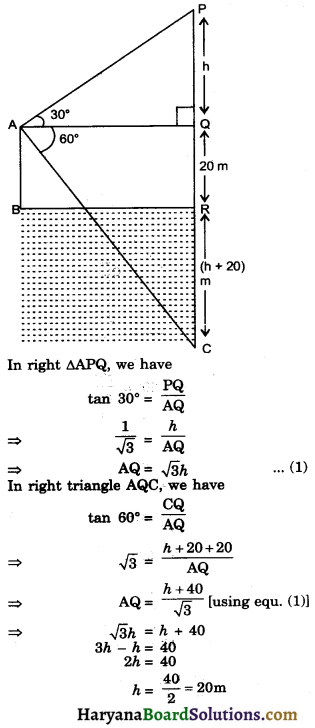
substituting the value of h in equ. (1), we get
AQ = \(\sqrt{3}\) × 20 = 20\(\sqrt{3}\)m
In right ΔAPQ, we have
⇒ AP² = AQ² + PQ²
⇒ AP² = (20\(\sqrt{3}\))² + (20)²
⇒ AP² = 1200 + 400
⇒ AP² = 1600
⇒ AP = \(\sqrt{1600}\)
⇒ AP = 40
Hence, distance of cloud from point A = 40 m.

Question 9.
Amit standing on a horizontal plane, find a bird flying at a distance of 200m. From him at an elevation of 30°. Deepak standing on the roof of a 50m hight building, find the angle of elevation of the same bird to be 45°. Amit and Deepak are on opposite sides of the bird. Find the distance of the bird from Deepak.
Solution :
Let A and B be two positions of Amit and Deepak. Let P be position of bird. Bird flying at a distance from A 200 m i.e. AP = 200 m. Angle of elevation of P from Amit is 30° i.e. ∠PAR = 30° and Angle of elevation of P from Deepak is 45° i.e.
∠PBQ = 45°

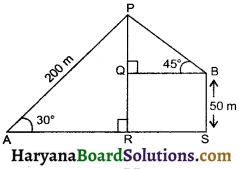
In right ΔAPR, we have
sin 30° = \(\frac {PR}{AP}\)
⇒ \(\frac {1}{2}\) = \(\frac{P Q+Q R}{200}\)
⇒ PQ + QR = \(\frac {200}{2}\)
⇒ PQ + 20 = 100 [∴ QR = BS]
⇒ PQ = 100 – 50 = 50 m
In right ΔPBQ, we have
sin 45° = \(\frac {PQ}{PB}\)
⇒ \(\frac{1}{\sqrt{2}}\) = \(\frac {50}{PB}\)
⇒ PB = 50\(\sqrt{2}\) m
Hence, distance of the bird from Deepak is 50\(\sqrt{2}\) m.

Question 10.
A vertical tower stands on a horizontal plane and is sur mounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and top of the flag staff are λ and β respectively. Prove that the height of the tower is \(\frac {h tan α}{tan β – tan α}\)
Solution :
Let AB be the vertical tower of height H and AD be flag staff of height h. The angle of elevation of bottom and top of flag staff are λ and β respectively i.e.
⇒ ∠ACB = α and
∠DCB = β

Hence proved.

Fill in the Blanks

Question 1.
……… is the height to which something is raised above a point of reference.
Solution :
Elevation

Question 2.
………. is the depth to which something is lowered below point of reference.
Solution :
depression

Question 3.
Numerically the angle of elevation is… to the angle of depression.
Solution :
equal

Question 4.
The angle of elevation and angle of depression both are measured with the ………. .
Solution :
horizontal

Question 5.
If two lines are ………, then the alternate interior angles formed are equal.
Solution :
parallel

Question 6.
Two angles having a sum of ………… are called complementary angles.
Solution :
90°

Question 7.
As the ……….. of an object increases, the angles of elevation of its top with the horizontal level also increases.
Solution :
height

Multiple Choice Questions

Choose the correct answer for each of the following:

Question 1.
A 20 m long ladder rests against a wall. If the feet of the ladder is 10 m away from the wall, then angle of the elevation is:
(a) 30°
(b) 60°
(c) 90°
(d) 45°
Solution :

Question 2.
When the sun is 30° above the horizontal, the length of the shadow casts by a 50 m high building is :
(a) 50\(\sqrt{3}\) m
(b) 25 m
(c) 25\(\sqrt{3}\) m
(d) \(\frac{50}{\sqrt{3}}\)m

Solution :
∵ Tan 30° = \(\frac {BC}{AB}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac {50}{AB}\)
⇒ Length of shadow AB = 50\(\sqrt{3}\) m
Hence correct choice is (a)

Question 3.
The angle of elevation of a tower from a distance 100 m from its foot is 30°. Height of tower is :
(a) 50\(\sqrt{3}\)
(b) 100\(\sqrt{3}\)
(c) \(\frac{100}{\sqrt{3}}\)
(d) \(\frac{50}{\sqrt{3}}\)
Solution :
In ΔABC

Hence, height of tower = \(\frac{100}{\sqrt{3}}\)m
Hence correct choice is (c).

Question 4.
A kite is flying at a height of 30 m from the ground. The length of string from the kite to the ground is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is :
(a) 45°
(b) 30°
(c) 60°
(d) 90°
Solution :
In ΔABC

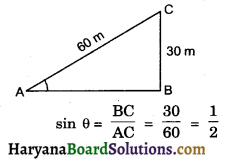
sin θ = sin 30°
⇒ θ = 30°
Hence angle of elevation 30°
So correct choice is (b).

Question 5.
If the elevation of the Sun changed from 30° to 60°, then difference between the length of shadows of a pole of height 15 m is :
(a) 7.5 m
(b) 15 m
(c) 103 m
(d) 573 m
Solution :
In ΔBCD

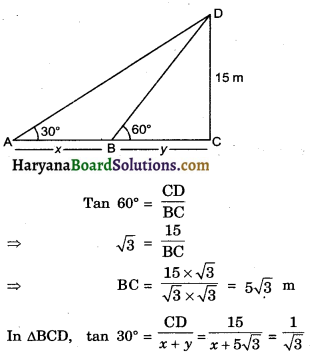
⇒ x + 5\(\sqrt{3}\) = 15\(\sqrt{3}\)
⇒ x = 15\(\sqrt{3}\) – 5\(\sqrt{3}\)
⇒ x = 10\(\sqrt{3}\) m
Hence required difference x = 10\(\sqrt{3}\) m
So correct choice is (c)

Question 6.
From a window 15 above the ground, the angle of elevation of the top of a tower is α and angle of depression of the foot of the tower is β. Then height of the tower is :
(tan α = \(\frac {5}{3}\), tan β = \(\frac {2}{3}\))
(a) 50 m
(b) 52.5 m
(c) 55 m
(d) 53.5 m
Solution :
Tan α = \(\frac {5}{3}\), Tan β = \(\frac {2}{3}\)
In ΔАВС Tan β = \(\frac{2}{3}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{15}{\mathrm{BC}}\)

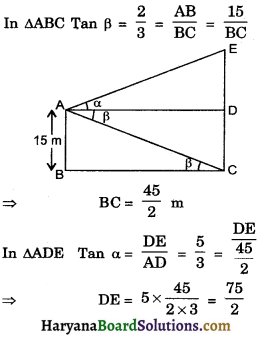
= 37.5 m
∴ Height of tower = CD + DE
= 15 + 37.5 m
= 52.5 m
So correct choice is (b).

Question 7.
A, B, C are three collinear points on the ground such that B lies between A and Cand AB = 10 m. If the angles of elevation of the top of a vertical tower at C are respectively 30° and 60° as seen from A and B, then the height of tower is :
(a) 5\(\sqrt{3}\) m
(b) 5 m
(c) \(\frac{10}{\sqrt{3}}\)
(d) \(\frac{20}{\sqrt{3}}\)
Solution :
Let CD = x, and BC = y
In ΔBCD,

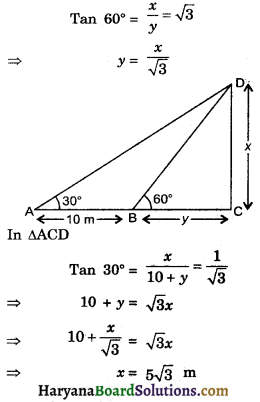
So correct choice is (a).

Question 8.
A person of height 2 m wants to get a fruit which is on a pole of height \(\frac {10}{3}\)m. If he stands at a distance of \(\frac {4}{3}\)m from the foot of the pole, then the angle at which he should throw the stone, so that it hits the fruits, is :
(a) 15°
(b) 30°
(c) 45°
(d) 60°
Solution :
From the figure

= Tan 45°
∴ θ = 45°
So correct choice is (c)