HBSE 10th Class Maths Important Questions Chapter 7 Coordinate Geometry

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 7 Coordinate Geometry Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 7 Coordinate Geometry

Short/Long Answer Type Questions

Question 1.
The distance between the point A(5, -3) and B(13, m) is 10 units. Calculate the value of m.
Solution :
Here, x₁ = 5, y₁ = – 3, x₂ = 13, y₂ = m
Distance (AB) = 10
⇒ \(\sqrt{(13-5)^2+(m+3)^2}\) = 10
⇒ \(\sqrt{8^2+m^2+9+6 m}\) = 10
⇒ \(\sqrt{64+m^2+9+6 m}\) = 10
⇒ \(\sqrt{73+m^2+6 m}\) = 10
⇒ [Squaring both sides]
⇒ m² + 6m + 73 – 100 = 0
⇒ m² + 6m – 27 = 0
⇒ m² + (9m – 3m) – 27 = 0
⇒ m² + 9m – 3m – 27 = 0
⇒ m(m + 9) – 3(m + 9) = 0
⇒ (m + 9) (m – 3) = 0
⇒ m + 9 = 0 or m – 3 = 0
⇒ m = – 9 or m = 3

Question 2.
If the distances of P(x, y) from A(5, 1) and B(-1, 5) are equal, then prove that 3x
Solution :
Since, of from A(5, 1) and B(-1, 5) are equal

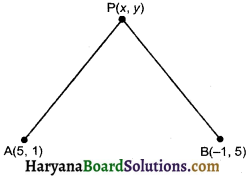
So, PA = PB
⇒ PA² = PB²
⇒ (5 – x)² + (1 – y)² = (-1 – x)² + (5 – y)²
⇒ 25 + x² – 10x + 1 + y² – 2y = 1 + x² + 2x + 25 + y² – 10y
⇒ 26 – 10x – 2y = 26 + 2x – 10y
⇒ – 10x – 2x = – 10y + 2y
⇒ – 12x = – 8y
⇒ 3x = 2y Hence proved.

Question 3.
It k(5, 4) is the mid point of line segment PQ and coordinates of Q are (2, 3) then find the coordinates of point P.
Solution :
Let coordinate of point P be (x, y)

Since k(5, 4) is mid point of P(x, y) and Q(2, 3)
∴ 5 = \(\frac{x+2}{2}\) and 4 = \(\frac{y+3}{2}\)
⇒ 10 = x + 2 and 8 = y + 3
⇒ x = 10 – 2 and y = 8 – 3
⇒ x = 8 and y = 5
∴ coordinates of point P are (8, 5)

Question 4.
If the midpoint of two points A(2, 5) and B(-5, y) is (-\(\frac {7}{2}\), 3). then find the distance between points A and B.
Solution :
Let point C(-\(\frac {7}{2}\), 3) is the midpoint of line AB.

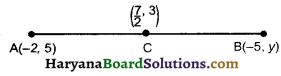
∴ 3 = \(\frac{5+y}{2}\)
⇒ 6 = 5 + y
⇒ y = 6 – 5 = 1
Coordinates of point is (-5, 1)
Length of AB = \(\sqrt{(-5+2)^2+(1-5)^2}\)
= \(\sqrt{(-3)^2+(-4)^2}\)
= \(\sqrt{9+16}\) = \(\sqrt{25}\) = 5
Hence, length of AB = 5 units.

Question 5.
In a parallelogram ABCD A(3, 1), B(5, 1), C(a, b) and D(4, 3) are the vertices. Find vertex C(a, b).
Solution :
We know that diagonals of a parallelogram bisects each other so, O is the mid point of AC as well as that of BD

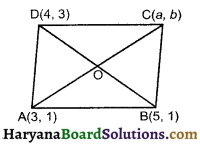
∴ Coordinates of mid point of AC = coordinates of mid point of BD
⇒ (\(\left(\frac{3+a}{2}, \frac{1+b}{2}\right)\)) = (\(\left(\frac{5+4}{2}, \frac{1+3}{2}\right)\))
⇒ (\(\left(\frac{3+a}{2}, \frac{1+b}{2}\right)\)) = (\(\frac {9}{2}\), \(\frac {4}{2}\))
⇒ \(\frac{3+a}{2}\) = \(\frac {9}{2}\) and \(\frac{1+b}{2}\) = \(\frac {4}{2}\)
⇒ 3 + a = 9 and l + b = 4
⇒ a = 9 – 3 and b = 4 – 1
⇒ a = 6 and b = 3
Hence, coordinates of vertex C is (6, 3)

Question 6.
If the coordinates of two adjacent vertices of a parallelogram are (3, 2), (1, 0) and diagonals bisect each other at (2, – 5), find the coordinates of the other two vertices.
Solution :
Diagonals of a parallelogram bisect each other.
Let coordinates of vertices C be (x₁, y₁) and d be (x₂, y₂) O is the mid point of AC as well as that of BD.

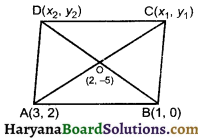
∴ coordinates of mid point of AC = (2, – 5)
⇒ (\(\frac{3+x_1}{2}, \frac{2+y_1}{2}\)) = (2, – 5)
⇒ \(\frac{3+x_1}{2}\) = 2, \(\frac{2+y_1}{2}\) = – 5
⇒ 3 + x₁ = 4, 2 + y₁ = – 10
⇒ x₁ = 1, y₁ = – 12
And coordinates of mid point of BD = (2, – 5)
⇒ (\(\frac{1+x_2}{2}, \frac{0+y_2}{2}\)) = (2, – 5)
⇒ \(\frac{1+x_2}{2}\) = 2, \(\frac{0+y_2}{2}\) = – 5
⇒ 1 + x₂ = 4, y₂ = – 10
⇒ x₂ = 3, y₂ = – 10
Coordinates of vertice Care (1, -12) and vertice D are (3, – 10).

Question 7.
If the midpoint of the line segment joining the points A(3, 4) and B(k, 6) is P(x, y) and x + y – 10 = 0. Find the value of k.
Solution :
Since, mid point’s coordinates are C(x, y)
∴ x = \(\frac{3+k}{2}\) and y = \(\frac{4+6}{2}\) = 5
Since (x, y) lies the equation x + y – 10, so

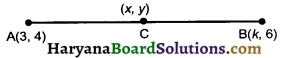
substituting the value, A(3, 4) of x, y in this equ., we get
\(\frac{3+k}{2}\) + 5 – 10 = 0
⇒ \(\frac{3+k}{2}\) – 5=0
⇒ \(\frac{3+k-10}{2}\) = 0
⇒ k – 7 = 0
⇒ k = 7
Hence, value of k is 7.

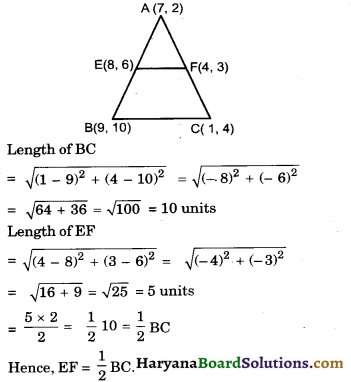
Question 8.
The coordinate of the vertices of ΔABC are A (7, 2), B (9, 10) and C(1, 4). If E and F are the mid points of AB and AC respectvely, prove that EF = \(\frac {1}{2}\)BC
Solution :
Since, E and f are the mid points of AB and AC respectvely coordinates of points are
\(\frac{9+7}{2}, \frac{10+2}{2}\) = (8, 6)
Coordinates of points Fare
\(\frac{1+7}{2}, \frac{4+2}{2}\) = (4, 3)

Question 9.
If the point C(-1, 2) divides in ternally the time segments joining A(2, 5) and B(x, y) in the ratio 3 : 4, find the coordinates of B.
Solution :
Hence, x₁ = 2, y₁ = 5, x₂ = x, y₂ = y, x = – 1, y = 2, m₁ = 3, m₂ = – 4

⇒ 3x + 8 = – 7 and 3y + 20 = 14
⇒ 3x = – 7 – 8 and 3y = 14 – 20
⇒ 3x = -15 and 3y = -6
⇒ x = –\(\frac {15}{3}\) and y = – \(\frac {6}{3}\)
⇒ x = – 5 and y = – 2
Hence, coordinate of point Bare (-5, -2)

Question 10.
In what ratio does the point P (\(\frac {24}{11}\), y) divide the line segment joining the points P(2, -2) and Q(3, 7) ? Also find the value y.
Solution :
Let the required ratio be k : 1
Here, x₁ = 2, y = – 2, x₂ = 3, y₂ = 7, x = \(\frac {24}{11}\), y = y
m₁ = k, m₂ = 1
By section formula, we have

Question 11.
Find the value of P, if the points A(2, 3) B(4, P) and C(6, – 3) are collinear.
Solution :
The given points are collinear So, the area of ΔABC will be zero.
Here, x₁ = 2, y₁ = 3, x₂ = 4, y₂ = P, x₃ = 6, y₃ = – 3
Area of ΔABC = 0
⇒ \(\frac {1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0
⇒ \(\frac {1}{2}\)[2 (P + 3) + 4 (-3 – 3) + 6 (3 – P)]= 0
⇒ \(\frac {1}{2}\)[2P + 6 – 24 + 18 – 6P] = 0
⇒ \(\frac {1}{2}\)[-4P + 0] = 0
⇒ – 4P = 0
⇒ P = 0

Question 12.
Find the area of triangle ABC with A(1, – 4) and the mid points of sides through A being (2, – 1) and (0, – 1).
Solution :
Let the coordinates of vertices B be (x₂, y₂) and C be (x₃, y₃)

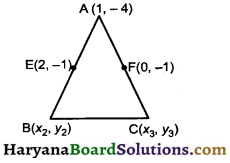
Let E (2, – 1) and f(0, – 1) are mid points of AB and AC respectively,
∴ 2 = \(\frac{1+x_2}{2}\) and – 1 = \(\frac{-4+y_2}{2}\)
⇒ 4 = 1 + x₂ and – 2 = – 4 + y₂
⇒ x₂ = 3 and y₂ = 2
∴ (x₂, y₂) = (3, 2)
Again 0 = \(\frac{1+x_3}{2}\) and – 1 = \(\frac{-4+y_2}{2}\)
⇒ 0 = 1 + x₃ and – 2 = – 4 + y₃
⇒ x₃ = – 1 and y₃ = 2
∴ (x₃, y₃) = (-1, 2)
Here, x₁ = 1, y₁ = – 4, x₂ = 3, y₂ = 2, x₃ = -1, y₃ = 2
Area of ABC
= \(\frac {1}{2}\)[x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= \(\frac {1}{2}\)[1(2 – 2) + 3 (2 + 4) + (-1)(-4 – 2)]
= \(\frac {1}{2}\)[1 × 0 + 3 × 6 + (-1) × (- 6)]
= \(\frac {1}{2}\)[0 + 18 + 6]
= \(\frac {1}{2}\) × 24 = 12
Hence, area of ABC = 12sq. units.

Question 13.
Prove that the points (2, -2), (2, 1) and (5, 2) are the vertices of a right angled triangle. Also find the area of this trian.
Solution :
Let the points A (2, -2), B (-2, 1) and C (5, 2) are the vertices of right angled triangle.
AB² = (-2 – 2)² + (1 + 2)²
= 16 + 9 = 25
BC² = (5 + 2)² + (2 – 1)² = 49 + 1 = 50
And AC² = (5 – 2)² + (2 + 2)²
= 9 + 16 = 25
AB² + AC² = 25 + 25 = 50 = BC²

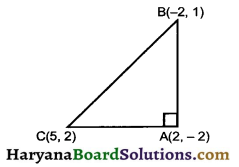
Since, BC² = AB² + AC², So by converse of phythagores theorem ∠A = 90° there fore point A (2, -2), B (-2, 1) and C (5, 2) are the vertices of a right angled triangle
Here, x₁ = 2, y₁ = -2, x₂ = -2, y₂ = – 1, x₃ = 5, y₃ = 2
Area of ΔABC
= \(\frac {1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac {1}{2}\)[2(1 – 2) + (-2)(2 + 2) + 5(-2 – 1)]
= \(\frac {1}{2}\)[2 × (-1) + (-2) × 4 + 5 × (-3)]
= \(\frac {1}{2}\)[- 2 – 8 – 15]
= \(\frac {1}{2}\)[-25]
= \(\frac {-25}{2}\)
Hence, area of Δ = \(\frac {25}{2}\)sq. units.

Question 14.
Find the area of that triangle whose vertices are (-3, -2), (5, -2) and (5, 4). Also prove that it is a right-angled triangle
Solution :
Let the points of vertices be A(-3, – 2), B (5, -2) and C (5, 4)
Here, x₁ = – 3, y₁ = – 2, x₂ = 5, y₂ = – 2, x₃ = 5 and y₃ = 4
Area of D ABC
= \(\frac {1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac {1}{2}\)[(-3)(-2 – 4) + 5 (4 + 2) + 5(-2 + 2)]
= \(\frac {1}{2}\)[(-3) × (-6) + 5 × 6 + 5 × 0)]
= \(\frac {1}{2}\)[18 + 30 + 0]
= \(\frac {1}{2}\) × 48 = 24 sq. units
AB² = (5 + 3)² + (-2 + 2)² = 8² + 0² = 64
BC² = (5 – 5)² + (4 + 2)² = 0² + 6² = 36
AC² = (5 + 3)² + (4 +2)² = 8² + 6² = 64 + 36 = 100
AB² + BC² = 64 + 36 = 100 = AC²

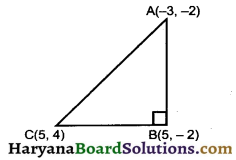
By converse of phythagoras theorem ∠B = 90° Hence, ΔABC is a right angled triangle.

Question 15.
In a ΔABC, A is (1, – 4). If E (0, -1) and Δ(2,-1) are the mid points of AB and AC. Calculate the area of ΔABC.
Solution :
Let the coordinates of vertices B is (x₂, y₂) and C is (x₃, y₃) since, E is the mid point of AB

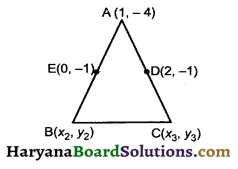
∴ 0 = \(\frac{1+x_2}{2}\) and – 1 = \(\frac{-4+y_2}{2}\)
⇒ 0 = \(\frac{1+x_2}{2}\) and – 2 = – 4 + y₂
⇒ x₂ = -1 and y₂ = – 2 + 4 = 2
(x₂, y₂) = (-1, 2)
Since, D is the midpoint of AC
∴ 2 = \(\frac{1+x_3}{2}\) and – 1 = \(\frac{-4+y_2}{2}\)
⇒ 0 = 1 + x₂ and – 2 = – 4 + y₂
⇒ x₂ = -1 and y₂ = – 2 + 4 = 2
∴ (x₃, y₃) = (-1, 2)
Since, D is the midpoint of AC.
∴ 2 = \(\frac{1+x_3}{2}\) and – 1 = \(\frac{-4+y_3}{2}\)
4 = 1 + x₃ and -2 = – 4 + y₃
x₃ = 3 and y₃ = 4 – 2 = 2
∴ (x₃, y₃) = (3, 2)
Here, x₁ = 1, y₁ = – 4, x₂ = – 1, y₂ = 2, x₃ = 3, y₃ = 2
Area of ΔABC
= \(\frac {1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac {1}{2}\)[1(2 – 2) + (-1) (2 + 4) + 3(-4 – 2)]
= \(\frac {1}{2}\)[1 × 0 + (-1) × 6 + 3 × (-6)]
= \(\frac {1}{2}\)[0 – 6 – 18]
= \(\frac {1}{2}\) × (-24) = – 12
Hence, area of ΔABC = 12 sq. units.

Question 16.
Find the area of the triangle formed by joining the mid points of the sides of a triangle, whose coordinates of vertices are (0, -1), (2, 1) and (0, 3).
Solution :
Let vertices of triangle be A (0, -1), B (2, 1) and (0, 3) in which of sides AB, BC and AC respectvely.

∴ Coordinates of point
(D) = \(\frac{1+0}{2}, \frac{1-1}{2}\) = (1, 0)
Coordinates of point
E = \(\frac{2+0}{2}, \frac{1+3}{2}\) = (1, 2)
And Coordinates of point
F = \(\frac{0+0}{2}, \frac{3-1}{2}\) = (0, 1)
Here, x₁ = – 1, y₁ = 0, x₂ = 1, y₂ = 2, x₃ = 0, y₃ = 1
Area of ΔDEF
= \(\frac {1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac {1}{2}\)[1 (2 – 1) + 1(1 – 0) + 0 (0 – 2)]
= \(\frac {1}{2}\)[1 × 1 + 1 × 1 + 0]
= \(\frac {1}{2}\) × (1 + 1)
= \(\frac {1}{2}\) × 2 = 1 sq. unit.
Hence, area of ΔDEF = 1sq. unit.

Fill in the Blanks

Question 1.
The point of intersection of two axes is called ……….
Solution :
origin

Question 2.
The distance of a point from the y axis is known its ………….
Solution :
abscissa

Question 3.
The ……… of a line segment divides the line segment in the ratio 1 : 1
Solution :
midpoint

Question 4.
If the area of a triangle is ……… sequare unit, then its vertices will be collinear.
Solution :
zero

Question 5.
The distance of a point from the x axis is called its …….
Solution :
ordinate

Question 6.
The distance of a point P(x, y) from the ………. is \(\sqrt{x^2+y^2}\)
Solution :
origin.

Multiple Choice Questions

Question 1.
The coordinates of the point which is reflection of point (-3, 5) in x axis are :
(a) (3, 5)
(b) (3, -5)
(c) (-3, -5)
(d) (-3, 5)

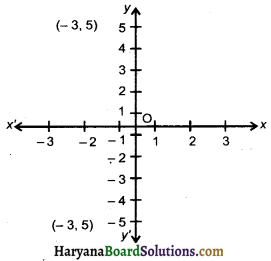
Solution :
(d) (-3, 5)

In graph paper we observe reflection of (-3, 5) in axis is (-3, -5).

Question 2.
The point P on x axis equidistant from the A(-1, 0) and B(5, 0) is:
(a) (2, 0)
(b) (0, 2)
(c) (3, 0)
(d) (2, 2)
Solution :
(a) (2, 0)

Since point P on x axis. So the coordinates of P(x, 0)

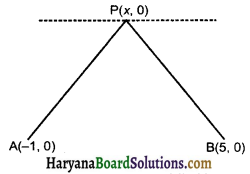
∵ Point P is equidistant from point A and point B.
∴ PA = PB
⇒ PA² = PB²
⇒ (-1 – x)² + (0 – 0)² = (5 – x)² + (0 – 0)²
⇒ 1 + x² + 2x + 0 = 25 + x² – 10x + 0
⇒ x² + 2x – x² + 10x = 25 – 1
⇒ 12x = 24
⇒ x = \(\frac {24}{12}\) = 2
Coordinates of point P(2, 0).

Question 3.
The distance between the points (acosθ + b sinθ, 0) and (0, asinθ – bcosθ), is :
(a) a² + b²
(b) a² – b²
(c) \(\sqrt{a^2+b^2}\)
(d) \(\sqrt{a^2-b^2}\)
Solution :
(c) \(\sqrt{a^2+b^2}\)

Let the given points A (a cosθ + b sinθ, 0) and (o, a sinθ – b cosθ)
The distance AB

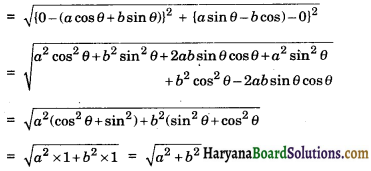
Question 4.
If the point P(6, 2) divides the line segment joining A(6, 5) and B(4, y) in the ratio 3 : 1, then the value of y is:
(a) 4
(b) 3
(c) 2
(d) 1
Solution :
(d) 1

The point P(6, 2) divides the line segment joining A(6, 2) and B(4, y) in the ratio 3 : 1

Here x₁ = 6, y₁ = 5, x₂ = 4, y₂ = y, m₁ = 3, m₂ = 1, x = 6, y = 2
By section formula

Question 5.
If the point P(k, 0) divides the line segment joining the points A(2, – 2) and B(-7, 4) in the ratio 1 : 2 then the value of k is :
(a) 1
(b) 2
(c) – 2
(d) – 1
Solution :
(d) – 1

Here, x₁ = 2, y₁ = – 2, x₂ = – 7, y₂ = 4, x = k, y = 0, m₁ = 1, m₂ = 2.
By section formula,

Question 6.
The value of P, for which the points A(3, 1), B(5, P) and C (7, – 5) are collinear is :
(a) – 2
(b) 2
(c) – 1
(d) 1.
Solution :
(a) – 2

the given points are collinear. So, area of ΔABC is zero.
Here, x₁ = 3, y₁ = – 1, x₂ = 5, y₂ = P, x₃ = 7, y₃ = – 5
Area of ΔABC = 0
⇒ \(\frac {1}{2}\)[x₁ (y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0
⇒ \(\frac {1}{2}\)[3(P + 5) + 5(-5 – 1) + 7(1 – P)] = 0
⇒ \(\frac {1}{2}\)[3P + 15 + 5(-6) + 7 – 7P] = 0
⇒ \(\frac {1}{2}\)[3P + 15 – 30 + 7 – 7P] = 0
⇒ \(\frac {1}{2}\)[-4P – 8] = 0
⇒ -4P = 8
⇒ P = \(\frac {8}{- 4}\)
⇒ P = – 2