Haryana State Board HBSE 10th Class Maths Important Questions Chapter 1 Real Numbers Important Questions and Answers.
Haryana Board 10th Class Maths Important Questions Chapter 1 Real Numbers
Short/Long Answer Type Questions
Question 1.
Show that square of any positive integer cannot be of the form (54 + 2) or (5q + 3) for any integer q.
OR
Prove that one of three consecutive positive integer is divisible by 3.
Solution :
Let be any positive integer and applying Euclid’s division Lemma it is of the form 5. For 5P + 1 or 5P + 2 or 5P + 3 or 5P + 4.
So, we have the following cases
Case I : When x = 5P
⇒ x2 = 25P2 = 5 (5P2)
⇒ x2 = 5q [Where q = 5P2]
Case II : When
x = 5P + 1
x2 = (5P + 1)2
= 25p2 + 10P + 1
= 5(5P2 + 2P) + 1
= 59 +1
[Where q = 5P2 + 2P]
Case III : When x = 5P + 2
x2 = (5P + 2)2
= 25P2 + 20P + 4
= 5(5P2 + 4P) + 4
= 59 + 4
(Where q = 5P2 + 4P)
Case IV : When x = 5P + 3
⇒ x2 = (5P + 3)2
= 25P2 + 30P + 4
= 25P2 + 30P + 5 + 4
= 5 (5P2 + 6P + 1) + 4
= 5 + 4
(Where q = 5P2 + 6P + 1)
Case V : When x = 5P + 4
⇒ x2 = (5P + 4)2
= 25P2 + 40P + 16
= 25P2 + 40P + 15 + 1
= 5(5P2 + 8P + 3) + 1
= 5q + 1
(Where q = 5P2 + 8P + 3)
So, square of any positive integer cannot be of the form (5q + 2) or (5q + 3).
Or
Solution :
Let x be any positive integer. By Euclid’s division lemma x = 3q + r, where 0 < r ≤ 3
[∴ r = 0, 1, 2]
Putting r = 0, we get
x = 3q + 0 = 3q which is divisible by 3.
Putting r = 1, we get
x = 3q + 1 which is not divisible by 3.
Putting r = 2, we get
x = 3q + 2, which is not divisible by 3.
So, one of every three consecutive positive integers is divisible by 3.
![]()
Question 2.
If n is an odd integer, then show that n2 – 1 is divisible by 8.
Solution :
We know that any odd positive integer x can be written in form 4q + 1 or 4q + 3
So, according to the question
Case I : When x = 4q + 1
Then, x2 – 1 = (4q + 1)2 – 1
= 16q2 + 8q + 1 – 1
= 89 (2q + 2) …(1)
Which is divisible by 8.
Case II : When x = 4q + 3
Then, x2 – 1 = (4q + 3)2 – 1
= 16q2 + 24q + 9 – 1
= 16q2 + 24q + 8
= 8(2q2 + 3 + 1) ………(2)
Which is divisible by 8. Therefore, from equations (1) and (2), it is clear that, if x is an odd positive integer. x2 – 1 is divisible by 8.
Question 3.
What is the HCF of the smallest prime number and the smallest composite number,
Solution :
Smallest prime number = 2
Smallest composite number = 4
∴ 2 = 2
and 4 = 2 × 2 = 22
HCF of (2, 4) 2.
![]()
Question 4.
Write the smallest number which is divisible by both 306 and 657.
Solution :
The required smallest number is the LCM of 306 and 657.
We have 306 = 2 × 3 × 3 × 17
= 2 × 32 × 17
And 657 = 3 × 3 × 73
= 32 × 73
LCM (306, 657) = 2 × 32 × 17 × 73
= 22938
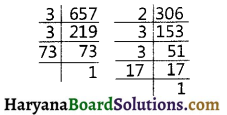
Hence, the required smallest number = 22338
Question 5.
The length, breadth and height of a room are 8m 50cm, 6m 26cm and 4m 75cm respectively. Find the length of longest rod that can measure the dimensions of the room exactly.
Solution :
Dimensions of a room are:
Length = 8m 50cm = 850 cm.
Breadth = 6m 25cm = 625 cm
And Height = 4m 75cm = 475 cm.
The required length of longest rod is the HCF of 850 cm, 625 cm and 475 cm.
850 = 2 × 5 × 5 × 17
= 2 × 52 × 17
625 = 5 × 5 × 5 × 5 = 54 And
475 = 5 × 5 × 19 = 52 × 19
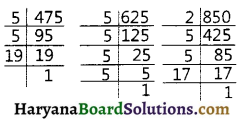
HCF of (850, 625, 475) = 52 = 25 cm
Hence, required length of longest rod = 25 cm.
![]()
Question 6.
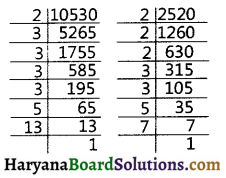
State the fundamental theorem of Arithmetic. Find the LCM of numbers 2520 and 10530 by prime factorization method.
Solution :
Fundamental Theorem of Arithmetic : Every composite number can be expressed (or factorized) as a product of primes, and this factorisation is unque, apart from the order in which the prime factors occur. Then factorisation of x can be written as x = P1 × P2 × P3, × ………. Px, Where P1, P2, ……..Px are primes and written in ascending order.
So, we have
2520 = 2 × 2 × 2 × 3 × 3 × 5 × 7
= 23 × 32 × 5 × 7
And 10530 = 2 × 3 × 3 × 3 × 3 × 5 × 13
= 2 × 34 × 5 × 13
LCM (2520, 10530) = 23 × 34 × 5 × 7 × 13
= 294840
Question 7.
Show that 3\(\sqrt{7}\) is an irrational number.
Solution :
Let us assume that 3\(\sqrt{7}\) is a rational. It can be expressed as form of \(\frac {a}{b}\),where a and b are coprime positive integers and b ≠ 0.
∴ 3\(\sqrt{7}\) = \(\frac {a}{b}\)[HCF of a and b is 1 and b ≠ 0]
⇒ \(\sqrt{7}\) = \(\frac {a}{3b}\) ……………(1)
⇒ \(\frac {a}{3b}\) = rational
[∵ a and b are positive integers]
So, from equ. (1) \(\sqrt{7}\) is rational number. But this contradicts the fact \(\sqrt{7}\) is irrational number. So, our asumption that 3\(\sqrt{7}\) is an irrational number, is wrong.
Hence, that \(\sqrt{6}\) is an irrational numbers.
Question 8.
Prove that \(\sqrt{6}\) is an irrational number.
Solution :
Let us assume that \(\sqrt{6}\) is rational. It can be express in the form of \(\frac {a}{3b}\), where a and b are coprime positive integers and b ≠ 0.
∴ \(\sqrt{6}\) = \(\frac {a}{b}\) (Where a and b are coprime ∴ HCF of a and b = 1 ……..(i)
⇒ 6 = \(\frac{a^2}{b^2}\) (Squaring both sides)
⇒ 6b2 = a2 ……………(i)
Therefore 6 divides a2. It follows that 6 divides a.
[By theorem 1.3]
Let a = 6c and put this value in equ. (i) we get
6b2 = (6c)2
⇒ 6b2 = 36c2
⇒ \(\frac{36 c^2}{6}\) = b2
⇒ 6c2 = b2 ………..(ii)
It means b2 is divisible by 6. It follows that b, is divisible by 6.
(By theorem 1.3)
From equations (i) and (ii) we say that 6 is a common factor of both a and b. But this contradicts the fact that a and b are coprime, so we have no common factor. So, our assumption that \(\sqrt{6}\) is a rational number is wrong. Therefore, \(\sqrt{6}\) is an irrational number. Proved.
![]()
Question 9.
Given that \(\sqrt{2}\) is an irrational number, then prove that (5 + 3\(\sqrt{2}\)) is an irrational number.
Solution :
Let us assume that 5 + 3\(\sqrt{2}\) is a rational number. It can be express in the form of \(\frac {a}{b}\), where a and b are coprime positive integers and b ≠ 0.
∴ 5 + 3\(\sqrt{2}\) = \(\frac {a}{b}\)
[Where HCF of a and b = 1]
⇒ 5 – \(\frac {a}{b}\) = 3\(\sqrt{2}\)
⇒ \(\frac{5 b-a}{b}\) = 3\(\sqrt{2}\)
⇒ \(\frac{5 b-a}{3}\) = \(\sqrt{2}\)
∵ a and b are positive integers
⇒ \(\frac{5 b-a}{3}\) is rational
Therefore, \(\sqrt{2}\) is rational But given that \(\sqrt{2}\) is irrational. So, our assumption that 5 + 3\(\sqrt{2}\) is rational is wrong.
Hence, 5 + 3\(\sqrt{2}\) is an irrational number.
Proved.
Question 10.
What type of decimal expansion does a rational number has? How can you distinguish it from decimal expansion of irrational numbers?
Solution :
A rational number may has its decimal expansion either terminating decimal expansion or a non-terminating repeating. But an irrational number has its decimal expansion non-repeating and non-terminating.
![]()
Question 11.
Write whether rational number \(\frac {7}{75}\) will have terminating decimal expansion or a non-terminating decimal.
Solution :
= \(\frac{7}{3 \times 5^2}\)
Since, denominator of given rational number is not form 2m × 5n.
Hence, it is non-terminating decimal expansion
Question 12.
After how many decimal places will the decimal expansion of \(\frac{23}{2^4 \times 5^3}\) terminate?
Solution :
We have
\(\frac{23}{2^4 \times 5^3}=\frac{23 \times 5}{2^4 \times 5^3 \times 5}=\frac{23 \times 5}{2^4 \times 5^4}\)
= \(\frac{115}{(10)^4}=\frac{115}{10000}\) = 0.0115
Hence, \(\frac{23}{2^4 \times 5^3}\) will terminate after 4 decimal places.
Fill in the Blanks
Question 1.
The sum or difference of a rational and an irrational number is.
Solution :
irrational
![]()
Question 2.
Every composite number can be factorized as the product of ………….
Solution :
primes
Question 3.
The product and quotient of a …………..rational and irrational number is irrational.
Solution :
non-zero
Question 4.
………………is the least prime and…………is the least composite number.
Solution :
2, 4
Question 5.
The HCF of two co-prime numbers is always …………..
Solution :
1
![]()
Question 6.
If a and b are co-primes, then a2 and b2 are …………….
Solution :
co-prime.
Multiple Choice Questions
Question 1.
Euclid’s division Lemma states that for two positive integers a and b, there exists unque integers q and r satisfying a = bq + r, and :
(a) o < r < b (b) 0 > r ≤ b
(c) 0 ≤ r < b
(d) 0 ≤ r ≤ b
Solution :
(c) 0 ≤ r < b
Question 2.
The total number of factors of prime numbers is :
(a) 1
(b) 0
(c) 2
(d) 3
Solution :
(c) 2
∵ We know that prime numbers h only two factors 1 and number itself.
![]()
Question 3.
Sum of the exponents of prime factors in the prime factorization of 196 is :
(a) 3
(b) 4
(c) 5
(d) 2
Solution :
(b) 4
∵ We have 196 = 2 × 2 × 7 × 7
= 22 × 72
It’s sum of exponents
= 2 + 2 = 4
Question 4.
The HCF and LCM of 12, 21, 15 respectvely are :
(a) 3, 140
(b) 12, 420
(c) 3, 420
(d) 420, 3
Solution :
(c) 3, 420
We have 12 = 2 × 2 × 3 = 22 × 3
21 = 3 × 7 × 3 × 7 and
15 = 3 × 5 = 3 × 5
LCM (12, 21, 15) = 22 × 3 × 5 × 7 = 420
And HCF (12, 21, 15) = 3
So, HCF and LCM of (12, 21, 15) = 3, 420
Question 5.
Which of the following rational number.
(a) \(\frac {1}{2}\)
(b) \(\frac {1}{2}\)
(c) \(\frac{343}{2^3 \times 5^2 \times 7^3}\)
(d) \(\frac{31}{2^4 \times 3^5}\)
Solution :
(c) \(\frac{343}{2^3 \times 5^2 \times 7^3}\)
![]()
Question 6.
The decimal representation of \(\frac{11}{2^3 \times 5}\) will :
(a) terminate after 1 decimal place
(b) terminate after 2 decimal place
(c) terminate after 3 decimal place
(d) not terminate
Solution :
(c) terminate after 3 decimal place
∵ Since, \(\frac{11}{2^3 \times 5}=\frac{11}{8 \times 5}=\frac{11}{40}\) = 0.275
So, \(\frac{11}{2^3 \times 5}\) will terminate after 3 decimal places.