HBSE 10th Class Maths Important Questions Chapter 5 Arithmetic Progressions

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 5 Arithmetic Progressions Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 5 Arithmetic Progressions

Short/Long Answer Type Questions

Question 1.
For what value of k will k + 9, 2k – 1 and 2k + 7 are the consecutive terms of an AP?
Solution :
The consecutive terms of an AP are k + 9, 2k – 1 and 2k + 7, then
2k – 1 = \(\frac{k+9+2 k+7}{2}\)
⇒ 4k – 2 = 3k + 16
⇒ 4k – 3k = 16 + 2
⇒ k = 18.

Question 2.
Find how many integers between 200 and 500 are divisible by 8.
Solution :
The numbers divisible by 8 between 200 and 500 are : 208, 216, 224,…..496, which an AP.
Here, a = 208, d = 8 and a_n = l = 496
We know that an = a + (n – 1)d
⇒ 496 = 208 + (n – 1) × 8
⇒ 496 – 208 = 8n – 8
⇒ 288 = 8n – 8
⇒ 288 + 8 = 8n
⇒ \(\frac {296}{8}\) = n
⇒ n = 37
Hence, required integer divisible by 8 = 37.

Question 3.
Find the middle term of an AP: 213, 205, 197……..
Solution :
The given sequence of an AP is 213, 205, 197, ………37
Here, a = 213, d = 205 – 213 = -8, l = 37
Let the number of terms ben
a_n = l = a + (n – 1)d
⇒ 37 = 213 + (n – 1) × (- 8)
⇒ 37 = 213 – 8n + 8
⇒ 8n = 221 – 37
⇒ n = \(\frac {184}{8}\) = 23
The middle term will be \(\frac{23+1}{2}\) i.e 12^th
So, a₁₂ = 213 + (12 – 1) × (-8)
= 213 – 88 = 125
Hence, middle term os AP is 125.

Question 4.
For what value of n are the nth terms of two APs : 63, 65, 67 …..and 3, 10, 17……..
Solution :
The two APs are 63, 65, 67,…. and 3, 10, 17……
Let a, d and A, D be Ist term and common difference of two given APs
Here, a = 63, d = 65 – 63 = 2 And
A = 3, D = 10 – 3 = 7
n^th terms of two APs are eqal
aⁿ = Aⁿ
⇒ a + (n – 1)d = A + (n – 1)D
⇒ 63 + (n – 1) × 2 = 3 + (n – 1) × 7
⇒ 63 + 2n – 2 = 3 + 7n – 7
⇒ 2n + 61 = 7n – 4
⇒ 61 + 4 = 7n – 2n
⇒ 65 = 5n
⇒ n = \(\frac {65}{5}\) = 13
Hence, 13^th term of two given APs are equal.

Question 5.
Write the nth terms of the AP:
\(\frac{1}{m}, \frac{1+m}{m}, \frac{1+2 m}{m}\) (CBSE-Comptt 2017)
Solution :
The given sequence of an APs is

Question 6.
Which term of the AP. 20, 19\(\frac {1}{4}\), 18\(\frac {1}{2}\), 17\(\frac {3}{4}\), is the first negative term. (CBSE 2020)
Solution :
The given sequence of AP is
20, 19\(\frac {1}{4}\), 18\(\frac {1}{2}\), 17\(\frac {3}{4}\), …………
Here, a = 20, d = 19\(\frac {1}{4}\) – 20 = \(\frac {-3}{4}\)
Let n^th term of an AP be the first negative term, then,

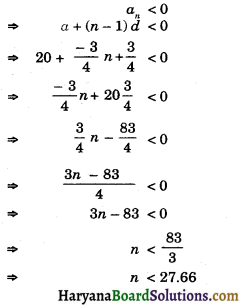
Hence, 28^th term of the AP is the first negative term.

Question 7.
If m times the m^th term of an AP is equal to n times its n^th term and m ≠ n, show the (m + n)^th term of AP is zero. [CBSE 2019]
Solution :
Let a be first term and d be common difference of AP.
We have, ma_m = na_n
⇒ m[a + (m – 1)d] = n[a + (n – 1)d]
⇒ ma + m²d – md = na + n²d – nd
⇒ m²d – n²d – md + nd = na – ma
⇒ d(m² – n²) – d(m – n) = a(n – m)
⇒ d[m² – n² – (m – n)] = a(n – m)
⇒ d[(m + n) (m – n) – (m – n)] = – a(m – n)
⇒ d[(m – n) (m + n – 1)] = – a(m – n)
⇒ d(m + n – 1) = \(\frac{-a(m-n)}{(m-n)}\)
⇒ d(m + n – 1) = – a
⇒ d = – \(\frac{a}{m+n-1}\)
Now, a_(m+n) = a + (m + n – 1)d
⇒ a_(m+n) = a + (m + n – 1) × – \(\frac{a}{(m+n-1)}\)
⇒ a_(m+n) = a – a = 0
Hence, (m + n)^th term = 0.

Question 8.
A manufactures of TV set produce 720 sets in fourth year and 1080 set in the sixth year, Assuming that the production increase uniformly by a fixed number every year, then find total production in first 9 year.
Solution :
Production of TV sets in 4th year = 720,
Production of TV sets in 6th year = 1080
Let a and d be first term and common difference respectively then,
a₄ = a + (4 – 1)d
⇒ 720 = a + 3d
⇒ a + 3d = 720 …….(1)
And a₆ = a + (6 – 1)d
⇒ 1080 = a + 5d
⇒ a + 5d = 1080 …….(2)
Substracting equ. (2) from equ. (1), We get

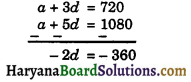
⇒ d = \(\frac {-360}{-2}\) = 180
Substituting the value of d in equ. (1), Weget
a + 3 × 180 = 720
⇒ a + 540 = 720
⇒ a = 720 – 540
⇒ a = 180
Production of TV sets increases uniformly by a fixed numbers.
So, Total productions of TV sets in first 9 year = a₉
a₉ = a + (9 – 1) 180
= 180 + 8 × 180
= 180 + 1440 = 1620
Hence, production in first 9^th year = 1620.

Question 9.
Find the sum of the first 20 terms of the following AP : 1, 4, 7, 10,……..
Solution :
The given sequence of AP is 1, 4, 7, 10 …………
Here, a = 1, d = 4 – 1 = 3, n = 20
We know that
S_n = \(\frac {n}{2}\)[2a + (n – 1)d]
= \(\frac {20}{2}\)(2 × 1 + (20 – 1) × 3]
= 10 (2 + 57)
= 10 × 59 = 590
Hence, sum of first 20 term = 590

Question 10.
Find the sum of all two digit natural numbers which are divisible by 4.
Solution :
The all two digit numbers which are divisible by 4 are :
12, 16, 20,…………..96
Here, a = 12, a_n = l =96, d = 16 – 12 = 4
∴ a_n = a + (n – 1)d
⇒ 96 = a + (n – 1)d
⇒ 96 = 12 + (n – 1) × 4
⇒ 96 = 12 + 4n – 4
⇒ 96 – 8 = 4n
⇒ 88 = 4n
⇒ n = \(\frac {88}{4}\) = 22
Sum of first 22 terms = S₂₂
∴ S₂₂ = \(\frac {22}{2}\)[12 + 96]
= 11 × 108 = 1188
Hence, sum of all two digit numbers divisible by 4 = 1188

Question 11.
How many terms of AP – 6, \(\frac {-11}{2}\), – 5, \(\frac {-9}{2}\), ………. are needed to give their sum zero.
Solution :
The given sequence of AP is
– 6, \(\frac {-11}{2}\), – 5, \(\frac {-9}{2}\), ……….
Here, a = – 6, d = \(\frac {-11}{2}\) – (-6) = \(\frac{-11}{2}+\frac{12}{2}=\frac{1}{2}\)
and S_n = 0 (given)
Let AP has n terms
S_n = 0
⇒ \(\frac {n}{2}\)[2a + (n – 1)d] = 0
⇒ \(\frac {n}{2}\)[2 × (-6) + (n – 1) × \(\frac {1}{2}\)] = 0
⇒ \(\frac {n}{2}\)[- 12 + \(\frac{n}{2}-\frac{1}{2}\)] = 0
⇒ \(\frac {n}{4}\)[- 24 + n – 1] = 0
⇒ n[- 25 + n] = 0
⇒ n² – 25n = 0
⇒ n(n – 25) = 0
⇒ n = 0 or n – 25 = 0
⇒ n = 0 or = n = 25
Reject n = 0
Hence, terms needed = 25

Question 12.
How many terms of the AP : 45, 39, 33………must be taken so that their sum is 180 ? explain the double answer.
Solution :
The given sequence of AP is 45, 39, 33, ………….
Here, a = 45, d = 39 – 45 = – 6 and S_n = 180 (given)
Let AP has n terms
S_n = 180
⇒ \(\frac {n}{2}\)[2a + (n – 1)d] = 180
⇒ \(\frac {n}{2}\)[2 × 45 + (n – 1)(-6)] = 180
⇒ \(\frac {n}{2}\)[90 – 6n + 6] = 180
⇒ \(\frac {n}{2}\)[96 – 6n] = 180
⇒ 96n – 6n² = 360
⇒ 6n² – 96n + 360 = 0
⇒ n² -16n + 60 = 0
⇒ n² – (10 + 6)n + 60 = 0
⇒ n – 10n – 6n + 60 = 0
⇒ n(n – 10) – 6 (n – 10) = 0
⇒ (n – 10)(n – 6) = 0
⇒ n = 10, or n = 6
Hence, 10 or 6 terms must be taken

Question 13.
Solve the equation : 1 + 4 + 7 + 10 + …… +x = 287
Solution :
The given equation is 1 + 4 + 7 + 10 +……+ x = 287
Here, a = 1, d = 4 – 1 = 3, a_n = x and S_n = 287
∴ a_n = a + (n – 1)d
⇒ x = 1 + (n – 1) × 3
⇒ x = 1 + 3n – 3
⇒ x = 3n – 2 ………….(i)
Also S_n = \(\frac {n}{2}\)[1 + l]
⇒ 287 = \(\frac {n}{2}\)[1 + x]
⇒ 287 = \(\frac {n}{2}\)[1 + 3n – 2]
⇒ 287 = \(\frac {n}{2}\)[3n – 1]
⇒ 574 = 3n² – n
⇒ 3n² – n – 574 = 0
By quadratic formula, we have
n = \(\frac{1 \pm \sqrt{(-1)^2-4 \times 3 \times(-574)}}{2 \times 3}\)
= \(\frac{1 \pm \sqrt{1+6888}}{6}=\frac{1 \pm \sqrt{6889}}{6}=\frac{1 \pm 83}{6}\)
⇒ n = \(\frac{1+83}{6}\) or n = \(\frac{1-83}{6}\)
⇒ n = 14 or n = \(\frac {- 41}{3}\) (Reject)
So, putting the value of n in equation (1), we get
x = 3 × 14 – 2 = 42 – 2 = 40
Hence, x = 40

Question 14.
If second and third terms of an AP are 3 and 5 respectvely, then find the sum of first 20 terms of it.
Solution :
Let a be first term and common difference bed of an AP
a₂ = 3
⇒ a + d = 3 ………..(1)
And a₃ = 5
⇒ a + 2d = 5 ……….(2)
Subtracting equ. (2) from equ. (1), we get

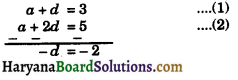
⇒ d = 2
Substituting the value of d in equ (1), we get
a + 2 = 3
⇒ a = 1
S₂₀ = \(\frac {20}{2}\)[2 × 1 + (20 – 1) × 2]
= 10 [2 + 38]
= 10 × 40 = 400
Hence,
S₂₀ = 400

Question 15.
If the sum of the first n terms of an AP is \(\frac {1}{2}\)(3n² + 7n), then find its nth terma. Hence write its 20^th terms.
Solution :
We have
S_n = \(\frac {1}{2}\)[3n² + 7n]
S₁ = \(\frac {1}{2}\)[3 × 1² + 7 × 1]
= \(\frac {1}{2}\) × 10 = 5
S₂ = \(\frac {1}{2}\)[3 × 2² + 7 × 2]
= \(\frac {1}{2}\)[12 + 14]
= \(\frac {1}{2}\) × 26 = 13
∴ a₁ = S₁ = 5, a₂ = S₂ – S₁ = 13 – 5 = 8
d = 8 – 5 = 3
So, AP is 5, 8, 11, ……………….
N^th term (a_n) =a + (n – 1)d
= 5 + (n – 1) × 3
= 5 + 3n – 3
= 3n + 2
And a₂₀ = 5 + (20 – 1) × 3
= 5 + 57 = 62.
Hence, AP is, 5, 8, 11, ………… and a₂₀ = 62

Question 16.
If the sum of first four terms of an AP is 40 and that of first 14 terms is 280. Find the sum of its n terms.
Solution :
Let first terms be a and common difference be d
S₄ = 40 (given)
⇒ \(\frac {4}{2}\)[2a + (4 – 1) × d] = 40
⇒ 2[2a + 3d] = 40
⇒ 2a + 3d = 20 …. (1)
And S₁₄ = 280
⇒ \(\frac {14}{2}\)[2a + (14 – 1)d] = 280
⇒ 2a + 13d = \(\frac {280}{7}\)
⇒ 2a + 13d = 40 ………(2)
Subtracting the equ (2) from equ. (1), we get

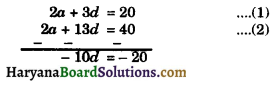
⇒ d = \(\frac {- 20}{- 10}\) = 2
Substituting the value of d in the equ. (1), we get
2a + 3 × 2 = 20
⇒ 2a + 6 = 20
⇒ 2a = 20 – 6 = 14
⇒ a = \(\frac {14}{2}\) = 7
Its sum of n^th term (S_n) = \(\frac {n}{2}\)[2a + (n – 1)d]
= \(\frac {n}{2}\)[2 × 7 + (n – 1) × 2]
= \(\frac {n}{2}\)[14 + 2n – 2]
= \(\frac {n}{2}\)[12 + 2n]
= n (6 + n) = n² + 6n
Hence, sum of its nth = n² + 6n.

Question 17.
Show that the sum of an AP whose first term is a, the second term b and the last term c, is equal to \(\frac{(a+c)(b+c-2 a)}{2(b-a)}\).
Solution :
We have, first term = a
second term = b
Then, common difference (d)
= b – a
last term (l) = c
Let n be the number of terms in the AP
∴ a_n = l = c
⇒ a + (n – 1) × (b – a) = c
⇒ (n – 1) (b – a) = c – a

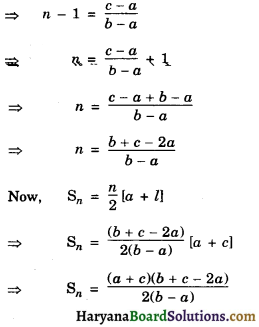
Hence Proved.

Question 18.
Find the sum of all 11 terms of an A.P. whose middle terms is 30.
Solution :
Let first term be a and common difference be d of, AP consisting of 11 terms, (\(\frac{11+1}{2}\))^th i.e. 6^th terms is middle terms. But it is given that middle most term is 30.
∴ a₆ = 30
⇒ a + (6 – 1)d = 30
⇒ a + 5d = 30
Sum of 11 terms (S₁₁) = \(\frac {11}{2}\)[2a + (11 – 1)d]
= \(\frac {11}{2}\)[2a + 10d]
= 11 (a + 5d)
= 11 × 30 [using eq. (1)]
= 330
Hence, S₁₁ = 330.

Question 19.
If in an A.P. the sum of first m times is n and the sum of its first n terms is m, then prove that the sum of its first (m + n) terms is -( m + n)
Solution :
Let first term be a and common difference be d of given A.P. then.
S_m = n (given)
⇒ \(\frac {m}{2}\)[2a + (m – 1)d] = n
⇒ 2ma + m (m – 1)d = 2n ………….(1)
And S_n = m (given)
⇒ \(\frac {n}{2}\)[2a + (n – 1)d] = m
⇒ 2na + n(n – 1)d = 2m ………….(2)
Substracting eq. (2) from eq. (1), we get

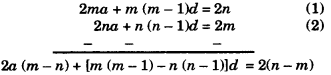
2a(m – n) + [m (m – 1) – n(n – 1)]d = 2(n – m)
⇒ 2a(m – n) + [(m² – m – n² + n)]d = – 2(m – n)
⇒ 2a(m – n) + [(m² – n²) – (m – n)]d = – 2(m – n)
⇒ 2a(m – n) + [(m + n) (m – n) – (m – n)d)] = 2(m – n)
(m – n)[2a + (m + n – 1)d] = – 2(m – n)
⇒ 2a + (m + n – 1)d = \(\frac{-2(m-n)}{(m-n)}\)
2a + (m + n – 1)d = – 2 ……..(3)
Now, S (m+n) = \(\frac{(m+n)}{2}\)[2a + (m + n – 1)d]
= \(\frac{(m+n)}{2}\) × (-2)
(using equation) ….(3)
= – (m + n)
Hence, S (m + n) = – (m + n)
Hence proved.

Question 19.
If m^th term of AP is \(\frac {1}{n}\) and n^th term is , find the sum of first mn terms.
Solution :
Let the first term of an AP is a and its common difference be d. them.
a_m = \(\frac {1}{n}\) …………(1)
⇒ a + (m – 1)d = \(\frac {1}{n}\)
And a_n = \(\frac {1}{m}\)
⇒ a + (n – 1)d = \(\frac {1}{m}\) …………(2)
Subtracting the equation (2) from (1), We get

Question 20.
A Motor car travels 175 km distance from place A to B, at a uniform speed 70km/ hr, passes through all ten green traffic signals. Due to heavy traffic it stops for one minute at first signal 3 minutes at second signal, 5 minutes at third signal and so on stops for 19 minutes at tenth signal How much total time to reach at the place B. Solve by suitable mathematical method.
Solution :
Distance travelled by car (s) = 175km.
Speed of a car (s) = 70km/hr.
Time taken by a car = \(\frac {D}{S}\)
to reach place AtoB = \(\frac {175}{70}\) hrs = \(\frac {5}{2}\)hours.
Due to heavy traffic a car stops at signal Iat to signal s 10 Time taken by a car at signal Ist to signal 10 = 1 min + 3 min + 5 min + ——- 19
Here a₁ = – 1, a₂ = – 3, a₃ = 5 and a_m = 19, n = 10.
Since, a₂ – a₁ = 3 – 1 = 2, a₃ – a₂ = 5 – 3 = 2,
a₃ – a₂ = a₂ – a₁
So, the given sequence form an AP
∴ S₁₀ = \(\frac {n}{2}\)[a + l]
= \(\frac {10}{2}\)[1 + 19]
= 5 × 20 = 100 min.
So, car stops at ten signal = 100 min
= \(\frac {100}{60}\)hrs
= 1\(\frac {40}{60}\)hrs
= 1\(\frac {2}{3}\) = \(\frac {5}{3}\)hrs
Total time taken by car = \(\frac{5}{2}+\frac{5}{3}=\frac{15+10}{6}\)
= \(\frac {25}{6}\) = 4\(\frac {1}{6}\)hrs

Question 21.
A Car travels 260km distance from place A to place B, at a uniform speed 65 km/hr passes through all thirreen green traffic signals, 4 minutes at first signal, 7 minutes at second signal 10 minutes at third signal and soon stops for 40 minutes at thirteen signal. How much total it takes to reach at the place B? Solve by suitable mathematical method.
Solution :
Distance covered from place A to B = 260 km/hr.
Speed of a car = 65km/hr
Time taken by a car = \(\frac{260}{65}=\frac{20}{5}\) = 4 hrs.
Car stops at thirteen green signals So, time taken by car at 13 green signals in
min = 4 + 7 + 10 + …….. 40
Since, a₂ – a₁ = 7 – 4 = 3, a₃ – a₂ = 10 – 7 = 3
a₃ – a₂ = a₂ – a₁ =
So, the given sequence form a_n AP
Here, a = 4, d = 3, a_n = 40 and n = 13
∴ S₁₃ = \(\frac {n}{2}\)[a + l]
= \(\frac {13}{2}\)[4 + 40]
= \(\frac {13}{2}\) × 44
= 13 × 12 = 156 min.
So, time taken (extra) by a car = 156 min
= \(\frac {156}{60}\) hrs
2\(\frac {36}{60}\)hrs = 2\(\frac {3}{5}\)hrs = \(\frac {13}{5}\)hrs
Total time taken by a car
= 4 + 2\(\frac {3}{5}\)hrs
= 6\(\frac {2}{5}\)hrs

Fill in the Blanks

Question 1.
If a, b, c are in AP, then ………… = \(\frac{a+c}{2}\) and b is called the airthmetic mean.
Solution :
b

Question 2.
The constant difference between any two consecutive terms of an AP is called the ……………. of the AP.
Solution :
commondifference

Question 3.
= \(\frac {x}{2}\)[2a + (n – 1)d]
Solution :
S_n

Question 4.
The common differeence of an AP can be positive, negative or ………..
Solution :
zero

Question 5.
An arithmetic progression is a list of numbers in which each term is obtained by adding or substracting a fixed number of the …………. term expect the first term.
Solution :
preceding

Question 6.
A ……….. may be difined as an arrangement of numbers in some definite order and according to some rule.
Solution :
sequence.

Multiple Choice Questions

Question 1.
The common difference of the AP.
\(\frac{1}{p}, \frac{1-p}{p}, \frac{1-2 p}{p}\) is :
(a) 1
(b) \(\frac {1}{p}\)
(c) – 1
(d) – \(\frac {1}{p}\)
Solution :
(c) The sequence of given AP is
\(\frac{1}{p}, \frac{1-p}{p}, \frac{1-2 p}{p}\), ………..
Common difference (d)
=\(\frac{1-\mathrm{P}}{\mathrm{P}}-\frac{1}{P}=\frac{1-\mathrm{P}-1}{\mathrm{P}}=\frac{-\mathrm{P}}{\mathrm{P}}\) = – 1

Question 2.
The n^th term of the AP. a, 3a, 5a, ……….
(a) na
(b) (2n – 1)a
(c) 2(2n + 1)
(d) 2na
Solution :
(b) The sequence of given AP is a, 3a, 5a …….
Here,
a₁ = a, d = 3a – a = 2a
n^th term (a_n) = a + (n – 1)d .
= a + (n – 1) × 2a
= a + 2na – 2a
= 2na – a
= a (2n – 1)

Question 3.
Value of x for which 2x, (x + 10) and (3x + 2) are there consecutive terms of an AP are :
(a) 6
(b) – 6
(c) 18
(d) – 18
Solution :
(a) Three consecutive terms of AP are 2x, (x + 10) and (3x + 2) Then,
x + 10 = \(\frac{2 x+3 x+2}{2}\)
⇒ 2x + 20 = 5x + 2
⇒ 20 – 2 = 5x – 2x
⇒ 18 = 3x
⇒ x = \(\frac {18}{3}\) = 6

Question 4.
The first term of AP is p and common difference is q, then its 10th term is :
(a) q + qp
(b) p – 9q
(c) p + 9q
(d) 2p + 9q.
Solution :
(c) p + 9q

a = p, d = q
a_n = a + (n – 1)d
⇒ a₁₀ = p + (10 – 1) = p + 9q

Question 5.
The 5th terms of the sequence defined by t₁ = 2, t₂ = 3 and t_n = t_n-1 + t_n-2 for n ≥ 3 :
(a) 16
(b) 13
(c) 15
(d) 2.
Solution :
(b) t₁ = 2, t₂ = 3

and t_n = t_n-1 + t_n-2
t₃ = t₂ + t₁ = 3 + 2 = 5
t₄ = t₃ + t₂ = 5 + 3 = 8
t₅ = t₄ + t₃ = 8 + 5 = 13
Hence correct choice is (b).

Question 6.
The sum of first 20 odd natural numbers is : ……………..
(a) 400
(b) 200
(c) 500
(d) 800.
Solution :
(a) Odd number is 1, 3, 5 ……
a = 1, d = 2, n = 20
S_n = \(\frac {n}{2}\)[2a + (n – 1)d]
= \(\frac {20}{2}\)[2 × 1 + 19 × 2]
= 10 × 40
= 400
So, correct choice is (a).