HBSE 10th Class Maths Important Questions Chapter 13 Surface Areas and Volumes

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 13 Surface Areas and Volumes Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 13 Surface Areas and Volumes

Short/Long Answer Type Questions

Question 1.
A copper rod of radius 1 cm and length 2 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution :
We have,
Radius of copper rod (r₁) = 1 cm
Length of copper rod (h₁) = 2 cm
Volume of copper rod = πr₁² × h₁
= π × 1² × 2
= 2π cm³
Let r² be radius of wire
Lenght of wire (h²) = 18 m
= 1800 cm

So, the diameter of the crossection i.e.
thickness of wire = \(\frac{2}{30}=\frac{1}{15}\)cm
= 0.67 mm (approx.)

Question 2.
A solid metallic sphere of diameter 16 cm is melted and recast into smaller solid cones, each of the radius 4 cm and height 8 cm. Find the number of cones so formed.
Solution :
We have,
Radius of sphere (R) = \(\frac {16}{2}\) = 8 cm
Volume of sphere = \(\frac {4}{3}\)πR³
= \(\frac {4}{3}\) × π × 8³
= \(\frac{4 \times 512 \pi}{3}\)cm³
radius of cone (r) = 4 cm
and height of cone (h) = 8 cm
Let the number of recast x cones be x
Volume of recast x cones
= x × \(\frac {1}{3}\)πr²h
= x × \(\frac {1}{3}\)π × 4² × 8
= \(\frac {128πx}{3}\)cm³

Since, solid sphere is melted and recast into smaller cones
∴ Volume of recast x cones = Volume of sphere
⇒ \(\frac{128 \pi x}{3}=\frac{4 \times 512 \pi}{3}\)
⇒ x = \(\frac{4 \times 512 \pi \times 3}{3 \times 128 \pi}\)
⇒ x = 16
Hence, number of recast cones = 16

Question 3.
A solid metallic cuboid of dimensions 9 m × 8m × 2 m is melted and recent into solid cubes of edges 2 m. Find the number of cubes so formed.
Solution :
We have,
Dimensions of cuboid = 9m × 8m × 2m
Volume of cuboid = 9 × 8 × 2
= 144 m³
edge of recast cube (a) = 2m
Volume of recast cube = a³
= (2)³ = 8m³
Let the number of recast cube be x
Since, cuboid is melted and recast into small x cubes
So, volume of x recasted cubes = Volume of cuboid
⇒ 8 × x = 144
⇒ x = \(\frac {144}{8}\) = 18
Hence, number of recast cubes = 18

Question 4.
A solid mettalic cylinder of radius 3.5 cm and height 14 cm is melted and recast into a number of small solid mettalic balls, each of radius \(\frac {7}{12}\)cm. Find the number of bass so formed.
Solution :
We have,
Radius of cylinder (R) = 3.5 cm
Height of cylinder (h) = 14 cm
Volume of cylinder = πr² h
= π × (3.5)² × 14 cm³
Andradius of recasted ball (r) = \(\frac {7}{12}\)cm
Volume of recasted small ball = \(\frac {4}{3}\)πr³
Let the number of recasted small balls be x
= \(\frac {4}{3}\)π(\(\frac {7}{12}\))³ cm³
since, cylinder is melted and recasted into x small balls
∴ Volume of x recasted = Volume of cylinder small balls

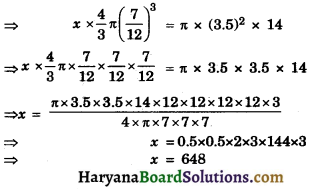
Hence, number of recasted smaller balls = 648

Question 5.
Find the number of coins of 1.5 cm diameter and 0.2 cm thickness to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Solution :
We have,
Radius of coins (r) = \(\frac {1.5}{2}\) = 0.75 cm
Thickness of coin (h) = 0.2
Volume of coin = πr²h
= π × (0.75)² × 0.2
= 1.125 π cm³
Let the number of recasted coins be x
∴ Volume of x coins = x × 1.125 πcm³
Radius of cylinder (R) = \(\frac {4.5}{2}\) = 2.25 cm
and Height of cylinder (H) = 10 cm
Volume of cylinder = πR²H
= π × (2.25)² × 10
= 50.625π cm³
Since, x coins to be melted to form a right circular cylinder
∴ Volume of x coins = Volume of cylinder
⇒ x × 1.125 π = 50.625π
⇒ x = \(\frac {50.625π}{1.125π}\)
⇒ x = 45
Hence, number of coins melted = 45

Question 6.
A sphere of diameter 12 cm is Iropped in a right circular cylindrical vessel, partly illed with water. If the sphere is completely ubmerged in water, the water level in the cylindrical vessel rises by 3\(\frac {5}{9}\) cm. Find the diameter of the cylindrical vessel.
Solution :
We have,
Diameter of sphere = 12 cm
Radius of the sphere (r) = \(\frac {12}{2}\) = 6 cm
Volume of the sphere = \(\frac {4}{3}\)πr³
= \(\frac {4}{3}\) × π × 6 × 6 × 6
= 288π

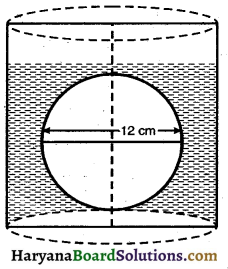
If sphere dropped into the cylinder, water rises by 3\(\frac {5}{9}\) cm
= \(\frac {32}{9}\)cm
∴ Height of the water rises in the cylinder (h) = \(\frac {32}{9}\) cm
Let radius of cylinder = R cm
Volume of the water rises that contained cylinder = πR²h
= π × R² × \(\frac {32}{9}\)
Volume of rises water of cylinder = Volume of the sphere
⇒ π × R² × \(\frac {32}{9}\) = 288π
⇒ R² = \(\frac{288 \pi \times 9}{32 \times \pi}\)
⇒ R² = 9 × 9
⇒ R = \(\sqrt{9 \times 9}\)
⇒ R = 9 cm.
∴ Diameter of the cylinder
= 2 × 9 = 18 cm.
Hence, diameter of the cylinder
= 18 cm.

Question 7.
Water is flowing at the rate of 5 km/hr through a pipe of diameter 14 cm into a rectangular tank of dimensions 50 m × 44 m. Find the time in which the level of water in the tank will rise by 7 cm.
Solution :
We have,
Speed of water in pipe = 5 km/hr
∴ Length of water flow in pipe in 1 hours.
= 5000 m
Let time consumes in it = t hour
Radius of pipe (r) = \(\frac {14}{2}\) = 7cm = \(\frac {7}{100}\)m
Volume of water flown in t hours through pipe = πr²H
= π × (\(\frac {7}{100}\))² × 5000 × t
= π × \(\frac {49}{100}\) × 5000 × t m ³
= 24.5 π × t m³
length of rectangle tank (l) = 50 m
Breadth of rectangle tank (b) = 44 m
Level of water rise (h) = 7 cm = \(\frac {7}{100}\)m
Volume of water in tank = l × b × h
= 50 × 44 × \(\frac {7}{100}\)
= 154 m³
Since, water flown through a pipe in the rectangular tank, so
Volume of water flawn through pipe in t hours = Volume of water in the tank
⇒ 24.5 π × t = 154
⇒ \(\frac{24.5 \times 22}{7}\) × t = 154
⇒ 77 × t = 154
⇒ t = \(\frac {154}{77}\)
⇒ t = 2 hours
Hence, time taken in which the level of water in the tank will rise by 7 cm = 2 hours.

Question 8.
Two spheres of same metal weight 1 kg and 7 kg. The radius of smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere.
Solution :
Radius of small sphere (r) = 3 cm
Volume of smaller sphere = \(\frac {4}{3}\)π × (3)³
= 36π cm³
Weight of smaller sphere is 1 kg and that of larger sphere is 7 kg
Since, 1 kg metal sphere occupies 36π cm³ sapse
How, weight of recasted metal sphere = 1 + 7 = 8 kg
∴ 8 Kg metal sphere occupies 36π × 8 cm³
Two sphere 1 kg and 7 kg mass melted and recast single sphere
Let the R be radius of recasted single sphere
∴ Volume of recasted single sphere = Volume of two 8 kg spheres
⇒ \(\frac {4}{3}\)πR³ = 36π × 8
⇒ R³ = \(\frac{36 \pi \times 8 \times 3}{4 \pi}\) = 216
⇒ R = 3\(\sqrt{6 \times 6 \times 6}\)
⇒ R = 6 cm
Hence, diameter of recasted new sphere = 2 × 6 = 12 cm.

Question 9.
504 cones each of diameter 3.5 em and hight 3 cm are melted and recast into a metallic sphere. Find the diameter of sphere and hence find its surface area. (use π = 22/7)
Solution :
We have,
Radius of each cone (r) = \(\frac {3.5}{2}\)
and its height (h) = 3 cm
Volume of 1 cone = \(\frac {1}{3}\)π × r²h
= \(\frac {1}{3}\)π × (\(\frac {3.5}{2}\))² × 3
= \(\frac {12.25}{4}\)π cm³
Volume of 504 cones = \(\frac{12.25 \pi \times 504}{4}\)
= 1543.5 π
Let the R be radius of recasted sphere volume of recasted sphere = \(\frac {4}{3}\)πR³
Since, 504 cones are melted and recast into metallic sphere
∴ Volume of recasted sphere = Volume of 504 cones

Hence, diameter of sphere 21 cm and its surface area = 1386 cm²

Question 10.
From each end of a solid metal cylinder, metal was scooped out in hemispherical form of same diameter. The height of the cylinder is 10 cm and its base is of radius 4.2 cm. The rest of the cylinder is melted and converted into at cylindrical wire of 1.4 cm thickness. find the length of wire. (use π = 22/7)
Solution :
We have,
Base radius of cylinder (R) = 4.2 cm
Height of cylinder (h) = 10 cm
Volume of cylinder = πR²h
= π × (4.2)² × 10
= 176.4π cm³
Volume of metal scooped out = 2 × volume of hemisphere

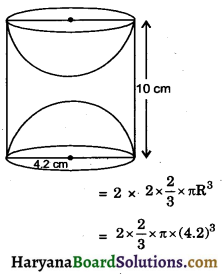
= 98.784π cm³
Volume of rest of cylinder
= 176.4π × 98.784π
= 77.616 π cm³
let the length of wire be l cm
∴ Volume of wire = πr²l [here H = 1 = π × (0.7)² × l]
[∴ radius of wire (r) = \(\frac {1.4}{2}\) = 0.7 cm]
= 0.49 πl
Since, rest of cylinder is melted and converted into a cylindrical wire.
∴ Volume of wire = Volume of rest of cylinder
⇒ 0.49πl = 77.616π
⇒ l = \(\frac {77.616л}{0.49π}\)
⇒ l = \(\frac {77.616}{0.49}\) = \(\frac {77.616}{49}\)
⇒ l = 158.4 cm
Hence, length of wire = 158.4 cm

Question 11.
A well of diameter 7 m is dug and earth from digging is evenly spread out to form a platform 22 m × 14 m × 2.5 m. Find the depth the well.
Solution :
We have,
Diameter of well = 7 m
∴ Its radius (r) = \(\frac {7}{2}\)m
Let depth of well be h m
Volume of soil dugout from well spread out to form a plateform.
So, volume of soil dugout from well = Volume of soil to form plateform
⇒ π × \(\frac {49}{4}\) × h = 770
⇒ h = \(\frac{770 \times 4}{49 \times \pi}\)
⇒ h = \(\frac{110 \times 4 \times 7}{7 \times 22}\)
⇒ h = 5 × 4 = 20 m
Hence, depth of well = 20 m

Question 12.
A well of diameter 4 m dug 21 m deep. The earth taken out of it has beed spread evenly all around it in the shape of a circular ring of width 3 m to form an embankment. Find the height of the embankment.

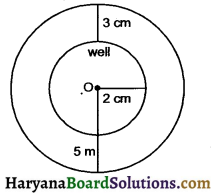
Solution :
We have,
Radius of the well (r) = \(\frac {4}{2}\) = 2 m
Depth of the well (h) = 21 m
Volume of the earth dug out = πr²h
= π × 2² × 21
= 84π m³
Radius of the embankment (R)
= 2 + 3 = 5 m
Let height of embankment be h’ m.
Volume of the earth used for making embankment = volume of the earth dugout
⇒ πr²h’ – πr²h’ = 84π
⇒ πh’ (R² – r²) = 84π
⇒ h’ (5² – 2²) = \(\frac {84π}{π}\)
⇒ h’ (25 – 4) = 84
⇒ h’ × 21 = 84
⇒ h’ = \(\frac {84}{21}\) = 4m
Hence, height of embankment is 4 cm.

Question 13.
Find the curved surface area of the frustum of a cone, the diameters of whose circular ends are 20 m and 6 m and its height is 24 m.

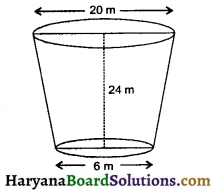
Solution :
We have,
Radii of two circular ends are :
r₁ = \(\frac {20}{2}\) = 10m, r₂ = \(\frac {6}{2}\) = 3m
And its height (h) = 24 m
Slant height of frustum of cone (l)
= \(\sqrt{h^2+\left(r_1-r_2\right)^2}\)
= \(\sqrt{24^2+(10-3)^2}\)
= \(\sqrt{576+49}\)
= \(\sqrt{625}\)
= 25 m
Curved surface area = πl(r₁ + r₂)
Frustum of a cone = 3.14 × 25 (10 + 3)
= 78.5 × 13
= 1020.5 m²

Question 14.
A bucket is in the form of a frustum of a cone of height 30 cm with raddi of its lower and upper ends as 10 cm and 20 cm, respectively. Find the capacity of the bucket. Also find the cost of milk which can completely fill the bucket at the rate of ₹ 40 per litre. (use π = 22/7)
Solution :
We have,
Raddi of lower and upper ends of frustum of a cone are
r₂ = cm and r₁ = 20 cm
And its height (h) = 30 cm
Capacity of bucket = Volume of bucket
= \(\frac {πh}{3}\)(r₁² + r₂² + r₁r₂)
= \(\frac{22}{7} \times \frac{30}{3}\)[(20)² + (10)² + 20 × 10]
= \(\frac {22}{7}\) × 10[400 + 100 + 200]
= \(\frac {220}{7}\) × 700
= 22000 cm³
Milk in the container = \(\frac {22000}{1000}\) liters
[∴ 1 litre = 1000 cm³]
= 22 litres
cost of milk = 22 × 40 = ₹880
Hence, capacity of bucket = 22 litres and cost of milk = ₹880

Question 15.
A metal container, open from the top, is in the shape of frustum of a cone of height 21 cm with raddi of its lower and upper circular ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of ₹35 per litre.
Solution :
We have,
Radii of lower and upper circular ends of a metal container open from the top are
r₂ = 8 cm, r₁ = 20 cm
and its height (h) = 21 cm
Volume of container = \(\frac {πh}{3}\)(r₁² + r₂² + r₁r₂)
= \(\frac{22}{3} \times \frac{21}{3}\)[(20)² + 8² + 20 × 8]
= 22 [400 + 64 + 160]
= 22 [624]
= 13728 cm³
= \(\frac {13728}{1000}\)
= 13.728 litres
cost of milk = 13.728 × 35
= ₹ 480.48

Question 16.
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of volume the two parts.
Solution :
Let VAB cone and VN be its axis, and let M be mid point of VN,

VN = 10 cm, VM = MN = \(\frac {10}{2}\)
Let VM be h’ = 5 cm
Let radii of upper and lower ends of frustum be r₁ cm and r₂ cm respectively
Δ VNB ~ Δ VMD [By AA similarity]

Hence, ratio of the required volumes = 1 : 7

Question 17.
A right circular cone is cut by two planes parallel to the base trisecting the height. Compare the volumes of the three parts into which the cone is divided.
Solution :
Let the right circular cone be cut by two parallel planes DE and FG.
∴ BC || DE || FG.
Now,
Δ ARG ~ ΔAPC
⇒ \(\frac {RG}{PC}\) = \(\frac {AR}{AP}\)

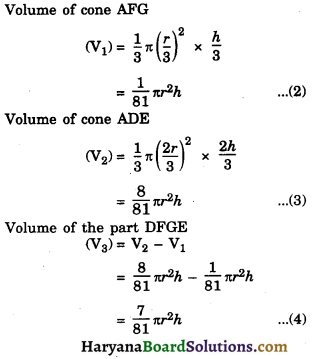
Fill in the Blanks

Question 1.
A playin top (lattu) consistr of a hemisphere and a _______
Solution :
cone

Question 2.
πl (r₁ + r₂) is _______ surface area of frusum.
Solution :
curved

Question 3.
In conversion of one solid to other solid, we have constant ________
Solution :
volume

Question 4.
Two spheres have raddi in the ratio 2 : 1, then ratio of their volume is _______
Solution :
8 : 1

Question 5.
While calculating the volumes of combi- nation of solids, the volume of common parts should be _______
Solution :
excluded

Question 6.
Volume of cylinder of radius r and height h is 27 cm³. Then the volume of cone of same radius and same height is _______ cm³.
Solution :
9

Question 7.
Bodies which have three dimensions in space are called ______.
Solution :
solids

Multiple Choice Questions

Question 1.
Volume of two spheres are in the ratio 64 : 27 the ratio of their surface areas is :
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) 16 : 9
Solution :
(d) 16 : 9

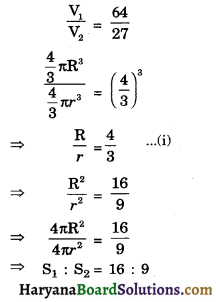
So correct choice is (d).

Question 2.
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that \(\frac {1}{8}\) space of the cube remains unfilled. Then the number of marbles that the cube can accommodate is :
(a) 142296
(b) 142396
(c) 142496
(d) 142596
Solution :
(a) 142296

Number of marbles

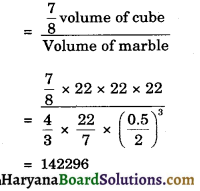
So correct choice is (a)

Question 3.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form at cone of base diameter 8 cm. The height of the cone is:
(a) 12 cm
(b) 14 cm
(c) 15 cm
(d) 18 cm
Solution :
(b) 14 cm

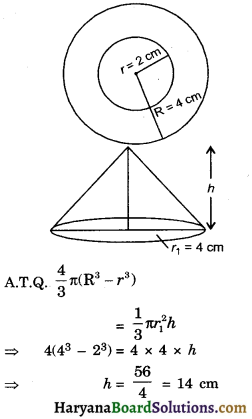
So correct choice is (b).

Question 4.
A solid piece of iron in the form of a cuboid of dimensions 49 cm × 33 cm × 24 cm, is moulded to form a solid slphere. The radius of the splhere is:
(a) 21 cm
(b) 23 cm
(c) 25 cm
(d) 19 cm
Solution :
(a) 21 cm

volume of sphere = volume of cuboid.
\(\frac {4}{3}\)πr³ = l × b × h
\(\frac {4}{3}\) × \(\frac {22}{7}\) × r³ = 49 × 33 × 24
r³ = 7³ × 3³
r = 7 × 3 = 21 cm
so correct choice is (a).

Question 5.
A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that \(\frac {1}{8}\) space is covered by the moter then the number of bricks used to construct the wall is :
(a) 11100
(b) 112000
(c) 11000
(d) 11300
Solution :
(b) 112000

So correct choice in 11200 i.e., (b).

Question 6.
Twelve solid spheres of the same size are made by melting a solid metallic cyclinder of base diameter 2 em and height 16 cm. The diameter of each sphere is :
(a) 4 cm
(b) 3 cm
(c) 2 cm
(d) 6 cm
Solution :
(c) 2 cm

volume of 12 sphere volume of cylinder
12 × \(\frac {4}{3}\)πr³ = πR²Н = π × 1 × 16
⇒ r = 1 cm
∴ d = 2r= 2 cm
So correct choice (c).

Question 7.
The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. The curved surface area of the bucket is
(a) 4950 cm²
(b) 4951 cm²
(c) 5952 cm²
(d) 4953 cm²
Solution :
(a) 4950 cm²

l = 45 cm, R = 28 cm, r = 7 cm
CSA = π(R + r)
= \(\frac {1}{2}\) × 45(28 + 7)
= \(\frac{22 \times 45 \times 35}{7}\)
= 4950 cm²
So correct choice is (a).

Question 8.
A medicine capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. the capacity of the capsule is:
(a) 0.36 cm³
(b) 0.35 cm³
(c) 0.34 cm³
(d) 0.33 cm³
Solution :
(a) 0.36 cm³

r = \(\frac {0.5}{2}\)cm
capacity of capsule


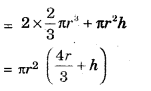
Hence correct choice is (a).