HBSE 10th Class Maths Important Questions Chapter 11 Constructions

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 11 Constructions Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 11 Constructions

Short/Long Answer Type Questions

Question 1.
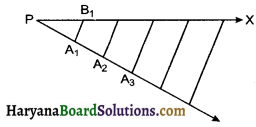
Construct a triangle with sides 4 cm, 5 cm and 7 cm and then another triangle whose sides are \(\frac {3}{4}\) of the corresponding sides of the first triangle.
Solution :
Steps of Construction :
1. Draw a line segment BC = 5 cm.
2. With B as centre and radius 4 cm draw and arc.
3. With C as centre and radius 7 cm draw another are to intersect the previous are at A.
4. Join AB and AC to get ΔABC
5. Draw any ray BX making an acute angle with BC on the opposite to the vertex A.

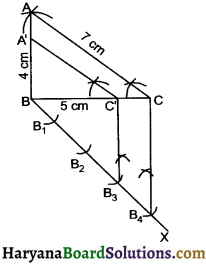
6. Along BX mark 4 points B₁, B₂, B₃ and B₄ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄
7. Join B₄C
8. From B₃ draw B₃C’ || B₄C meeting BC at
9. From C’ draw A’C’ || AC meeting AB at A’. Then A’BC’ is required triangle, each of whose side is \(\frac {3}{4}\) of corresponding sides of ΔABC.

Justification: Since
A’C’ || AC
Therefore, A’BC’ ~ ΔABC
\(\frac {A’B}{AB}\) = \(\frac {BC’}{BC}\) = \(\frac {A’C’}{AC}\) = \(\frac {3}{4}\)

Question 2.
Construct a triangle with sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac {3}{5}\) times of the corresponding sides of the given triangle.
Solution:
Steps of Construction:
1. Draw a line segment QR = 4 cm.

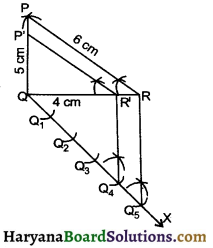
2. With Q as centre and radius 5 cm draw an
3. With R as centre and radius 6 cm draw another are to intersect the previous arc at P.
4. Join PQ and PR to get ΔPQR
5. Draw any ray QX making an acute angle with QR on the opposite to the vertex P.
6. Along QX mark 5 points Q₁, Q₂, Q₃, Q₄ and Q₅ such that QQ₁ = Q₁Q₂ = Q₂Q₃ = Q₃Q₄ = Q₄Q₅
7. Join Q₅R
8. From Q₃ draw Q₃R’ || Q₅R meeting QR at R’
9. From R’ draw R’P’ || PR. Then P’ QR’ is required triangle.
Justification: Since
P’R’ || PR
Therefore, P’QR’ ~ ΔPQR
\(\frac {P’Q}{PQ}\) = \(\frac {QR’}{QR}\) = \(\frac {P’R’}{PR}\) = \(\frac {3}{5}\)

Question 3.
Construct a ΔABC with AB = 6 cm, BC = 5 cm and ∠B = 60°. Now construct another triangle whose sides are \(\frac {2}{3}\) times the corresponding sides of ΔABC.
Solution :
Steps of Construction :
1. Draw a line segment BC = 5 cm.
2. At B, draw ∠CBY = 60°
3. From B, draw and are AB = 6 cm meeting by at A

4. Join AC. Thus, ΔABC obtained
5. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
6. Along BX mark 3 points B₁, B₂, and B₃ such that BB₁ – B₁B₂ = B₂B₃
7. Join B₃C
8. From B₂ draw B₂C’ || B₃C meeting BC at C
9. From C’ draw A’C’ || AC meeting AB at A’. Then A’BC’ is required triangle, each of whose side is  \(\frac {2}{3}\) of corresponding sides of ΔABC

Justification: Since
A’C’ || AC
Therefore, A’BC’ in ΔABC
\(\frac {A’B}{AB}\) = \(\frac {BC’}{BC}\) = \(\frac {A’C’}{AC}\) = \(\frac {2}{3}\)

Question 4.
Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are \(\frac {3}{5}\) of the corresponding sides of ΔABC.
Solution:
Steps of Construction:
1. Draw a line segment AB = 5 cm.

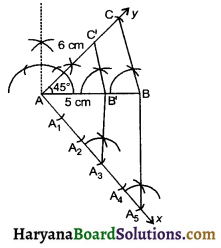
2. At A, draw ∠BAY = 45°
3. From A draw an arc AC = 6 cm meeting A at C
4. Join BC. Thus, ΔABC obtained.
5. Draw any ray AX making an acute angle with AB on the side opposite to the vertex C.
6. Along AX mark 5 points A₁, A₂, A₃, A₄ and A₅ such that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅
7. Join A₅B
8. From A₃ draw A₃B’ || A₅B meeting AB at B’
9. From B’ draw B’C’ || BC meeting AC at C’.
Then AB’C’ is required triangle, each of whose side is \(\frac {3}{5}\) of corresponding sides of ΔABC.
Justification: Since
B’C’ || BC
Therefore, AB’C’ ~ ΔABC
\(\frac {AB’}{AB}\) = \(\frac {B’C’}{BC}\) = \(\frac {AC’}{AC}\) = \(\frac {3}{5}\)

Question 5.
Draw a ΔABC in which BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct another triangle whose sides are \(\frac {3}{4}\) times corresponding sides of ΔABC.
Solution:
Steps of Construction:
1. Draw a line segment BC = 7 cm.

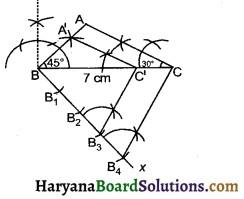
2. In ΔABC, ∠B = 45°, 2A = 105°
∴ ∠C = 180° – (45° + 105°) = 30°
At B draw and angle ∠B = 45° and draw ∠C = 30° intersecting each other at A to get ΔABC
3. At B draw any ray BX making an acute angle with BC on the side opposite to the vertex A
4. Along BX mark 4 points B₁, B₂, B₃ and B₄ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄
5. Join B₄C
6. From B₃ draw B₃C’ || B₄C meeting BC at C’
7. From C’ draw C’A’ || AC meeting AB at A
Then A’BC’ is required triangle, each of whose side is \(\frac {3}{4}\) of corresponding sides of ΔABC.

Justification: Since
A’C’ || AC
Therefore, A’BC’ ~ ΔABC
\(\frac {A’B}{AB}\) = \(\frac {BC’}{BC}\) = \(\frac {A’C’}{AC}\) = \(\frac {3}{4}\)

Question 6.
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are \(\frac {3}{4}\) times the corresponding sides of ΔABC.
Solution :
Steps of Construction:
1. Draw a line segment BC = 7 cm.
2. In ΔABC, ∠B = 45°, 2A = 105°
∴ ∠C = 180° – (45° + 105°) = 30°
At B draw and angle ∠B = 45° and draw ∠C = 30° intersecting each other at A to get ΔABC
3. At B draw any ray BX making an acute angle with BC on the side opposite to the vertex A
4. Along BX mark 4 points B₁, B₂, B₃ and B₄ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄
5. Join B₄C
6. From B₃ draw B₃C’ || B₄C meeting BC at C’
7. From C’ draw C’A’ || AC meeting AB at A
Then A’BC’ is required triangle, each of whose side is \(\frac {3}{4}\) of corresponding sides of ΔABC.

Justification: Since
A’C’ || AC
Therefore, A’BC’ ~ ΔABC
\(\frac {A’B}{AB}\) = \(\frac {BC’}{BC}\) = \(\frac {A’C’}{AC}\) = \(\frac {3}{4}\)

Question 7.
How many tangents can be constructed to any point on the circle of radius 4 cm ?
Solution :
We know that, if a point lies on the circle, then there is only one tangent to the circle at this point. So, one tangent can be constructed to any point on the circle of radius 4 cm.

Question 8.
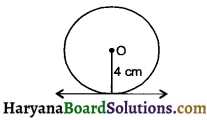
Draw a circle of radius 3.5 cm. From a point P, 6 cm from its centre, draw two tangents to the circle.
Solution :
Steps of Construction :
1. Draw a circle with O as the centre and radius 3.5 cm
2. Mark a point P outside the circle such that OP = 6 cm.
3. Join OP and draw prependicular bisector of PO meeting PO at M.,
4. Draw a circle with M as the centre and radius equal to PM = OM intersecting the given circle at points Q and R.

5. Join PQ and PR then PQ and PR are required tangents.

Question 9.
Draw a circle of radius 2 cm with centre O and take a point P outside the circle such that OP = 6.5 cm. From P, draw two tangents to the circle.
Solution :
Steps of Construction :
1. Draw a circle with O as the centre and radius 2.0 cm
2. Mark a point P outside the circle such that OP = 6.5 cm.
3. Join OP and draw perpendicular bisector of PO meeting PO at M

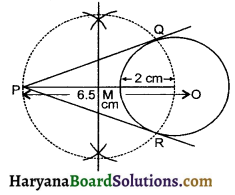
4. Draw a circle with M as the centre and radius equal to PM = OM intersecting the given circle at points Q and R.
5. Join PQ and PR then PQ and PR are required tangents.

Question 10.
Draw a pair of tangents to a circle of radius 5 cm, which are inclined to each other at an angle of 70°.
Solution :
Steps of Construction:
1. Draw a circle with centre O and radius 5 cm
2. Construct raddi OA and OB such that ∠AOB = 360° (90° + 90° + 70°) = 110°.
3. Draw AL ⊥ OA at A and BM ⊥ OB at B. They intersect at P.
4. Then PA and PB are the required tangents inclined to each other at 70°.

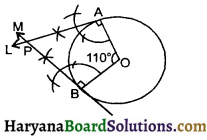
Justification: PA ⊥ OA and PB ⊥ OB and ∠AOB = 110°
∠APB = 360° – (90° + 90° + 110°)
∠APB = 360° – 290°
∠APB = 70°
Therefore, tangents PA and PB are inclined at 60°

Question 11.
Draw a circle of radius 5 cm. From a point 13 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Also verify the measurement by actual calculation.
Solution:
Steps of Construction:
1. Draw a circle with centre O of radius 5 cm
2. Mark a point A, 13 cm away from the centre.
3. Join AO and bisect it at M.
4. Draw a circle with M as the centre and radius equal to AM intersects the given circle at points P and Q.
5. Join AP and AQ

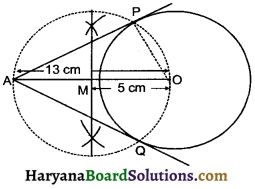
Then AP and AQ are the required tangents lengths of AP and AQ are 12 cm.

Justification:
Join OP
∴ ∠APO = 90°
[Angle is a semicircle]
AP ⊥ OP
Therefore, AP is a tangent to the given circle. Similarly AQ is a tangent to the given circle.
In right triangle APO, we have
AO² = PO² + AP²
13² = 5² + AP²
169 – 25 = AP²
AP = \(\sqrt{144}\)
AP = 12 cm

Fill in the Blanks

Question 1.
The part of a curve between two given points on the curve is known as……….
Solution :
Curve

Question 2.
……. is a straight line which touches the circle at one point only.
Solution :
tangent

Question 3.
There can be ……. tangents drawn to the circle from point in side it.
Solution :
no

Question 4.
The angle between radius and tangents is …… a angle.
Solution :
right

Question 5.
To draw a ……. at a given point to the circle, We simply draw radius at this point and draw a line perpendicular through this point.
Solution :
tangent.

Multiple Choice Questions

Choose the correct answer in each of the following:

Question 1.
In the given figure, if PA₁ =A₁A₂ = A₂A₃ = A₄Q and A₁B₁ || A₂B₂ || A₃B₄ || A₄B₄ || QR. Then A₂ divides the line segment PR in the ratio:

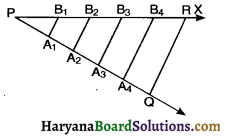
(a) 2 : 2
(b) 2 : 3
(c) 1 : 2
(d) 3 : 2
Solution :
From fig it is clear that A₂ divides the line segment PR in the ratio 2 : 3.

So correct choice is (b)

Question 2.
In the above figure, A₃ divides the line segment PR in the ratio :
(a) 3 : 5
(b) 2 : 3
(c) 3 : 2
(d) 3 : 6
Solution :
A₃ divides the line segment PR in the ratio 3 : 2
So, correct choice is (c)

Question 3.
In the above figure A, divides the line segment in the ratio :
(a) 1 : 1
(b) 1 : 2
(c) 1 : 4
(d) 1 : 5
Solution :
Here, A₁ divides the line segment in the ratio 1 : 4.
So correct choice is (c).

Question 4.
To divide a line segment AB in the ratio 4 : 7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A₁, A₂, A₃, … are located at equal distances on the ray AX and the point B is joined to:
(a) A₁₂
(b) A₁₁
(c) A₁₀
(d) A₉
Solution :
4 + 7 = 11
∴ A₁₁
Hence correct choice is (b).

Question 5.
To construct a triangle similar to a given ΔABC with its sides \(\frac {3}{7}\) of the corresponding sides of ΔABC, first draw a ray BX such that ∠CBX is an acute angle and X lies on the opposite side of A with respect to BC. Then locate points B₁, B₁, B₁, …. on BX at equal distance and next step is to join :
(a) B₁₀ to C
(b) B₃ to C
(c) B₇ to C
(d) B₄ to C
Solution :
B₇ to C
So correct choice is (c).

Question 6.
To divide a line segment AB in the ratio 3 : 4. We draw a ray ∠BAX, so that is an acute angle and then marks the points on the ray AX at equal distances such that the minimum number of these points is :
(a) 3
(b) 7
(c) 4
(d) 12
Solution :
3 + 4 = 7
So correct choice is (b).

Question 7.
To construct a triangle similar to a given ΔABC with its sides \(\frac {8}{5}\) of the corresponding sides of ΔABC draw a ray BX such that ∠CBX is an acute angle and X is on the opposite side of A with respect to BC. The minimum number of points to be located at equal distances on ray BX is :
(a) 5
(b) 8
(c) 13
(d) 3
Solution :
8
so correct choice is (b).

Question 8.
To divide a line segment AB in the ratio 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray by parallel to AX and the points A₁, A₂, A₃, and B₁, B₂, B₃, … are located at equal distances on the ray AX and BY, respectively. Then the points joined are :
(a) A₅ and B₆
(b) A₆ and B₅
(c) A₄ and B₅
(d) A₅ and B₄
Solution :
So, the points joined are A₅ and B₆ [By Prop. of similar Δs]

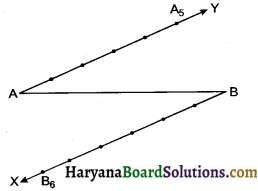
So correct choice is (a).