HBSE 10th Class Maths Important Questions Chapter 1 वास्तविक संख्याएँ

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 1 वास्तविक संख्याएँ Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 1 वास्तविक संख्याएँ

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न

प्रश्न 1.
240 और 6552 का HCF यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग करके ज्ञात कीजिए ।
हल :

यूक्लिड विभाजन एल्गोरिथ्म से-
6552 = 240 × 27 + 72
240 = 72 × 3 + 24
72 = 24 × 3 + 0
क्योंकि यहाँ पर शेषफल शून्य तथा भाजक 24 है।
इसलिए 240 और 6552 का HCF = 24

प्रश्न 2.
दर्शाइए कि कोई भी धनात्मक पूर्णांक 3q या 3q + 1 या 3q + 2 के रूप का होता है, जहाँ q कोई पूर्णांक है।
हल :
माना a एक धनात्मक पूर्णांक है तथा b = 3 हो तो यूक्लिड विभाजन एल्गोरिथ्म से-
a = 3q + r
क्योंकि 0 ≤ r < 3 है, इसलिए संभावित शेषफल 0, 1 या 2 हो सकते हैं ।
अर्थात् a संख्याओं 3q, 3q + 1 या 3q + 2 के रूप का हो सकता है जहाँ q कोई पूर्णांक है ।

प्रश्न 3.
निम्नलिखित संख्याओं को \(\frac {p}{q}\) के रूप में व्यक्त कीजिए-
(i) 0.375
(ii) 0.104
(iii) 0.15
(iv) 15.75
हल :

प्रश्न 4.
एक मिठाई विक्रेता के पास 420 काजू की बर्फियाँ और 130 बादाम की बर्फियाँ हैं । वह इनकी ऐसी ढेरियाँ बनाना चाहती है कि प्रत्येक ढेरी में बर्फियों की संख्या समान रहे तथा ये ढेरियाँ बर्फी की परात में न्यूनतम स्थान घेरें । इस काम के लिए प्रत्येक ढेरी में कितनी बर्फियाँ रखी जा सकती हैं?
हल :
प्रश्नानुसार, यहाँ पर हमें 420 और 130 का HCF यूक्लिड एल्गोरिथ्म द्वारा ज्ञात करना है-

420 = 130 × 3 + 30
130 = 30 × 4 + 10
30 = 10 × 3 +0
क्योंकि यहाँ पर शेषफल शून्य तथा भाजक 10 है ।
इसलिए 420 और 130 का HCF = 10
अतः प्रत्येक प्रकार की बर्फी के लिए मिठाई विक्रेता 10-10 की ढेरी बना सकता है

प्रश्न 5.
8232 को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए ।
हल :

8232 = 2 × 2 × 2 × 3 × 7 × 7 × 7
= 2³ × 3 × 7³

प्रश्न 6.
सिद्ध कीजिए कि \(\sqrt{2}\) एक अपरिमेय संख्या है।
हल :
माना \(\sqrt{2}\) एक परिमेय संख्या है जो कि दिए गए के विपरीत है।
अब \(\sqrt{2}\) = \(\frac {a}{b}\) जहाँ a और b सह-अभाज्य पूर्णांक हैं तथा b ≠ 0 है।
⇒ \(\sqrt{2}\)b = a
दोनों ओर का वर्ग करने पर, 2b² = a² ………..(i)
इससे पता चलता है कि a², 2 से विभाज्य है, इसलिए a भी 2 से विभाज्य होगी। ………..(ii)
⇒ a = 2m जहाँ m एक पूर्णांक है ।
a का मान समीकरण (i) में रखने पर,
2b² = (2m)²
⇒ 2b² = 4m²
या b² = 2m²
इसका अर्थ यह है कि 2 से b² विभाजित हो जाता है इसलिए b भी 2 से विभाजित होगा । ………….(iii)
इसी प्रकार समीकरण (ii) व (iii) से a और b में कम-से-कम एक उभयनिष्ठ गुणनखंड 2 है। इससे हमारी कल्पना गलत होती है कि a और b सह-अभाज्य हैं । अतः सिद्ध है कि \(\sqrt{2}\) एक परिमेय संख्या नहीं है।
अतः \(\sqrt{2}\) एक अपरिमेय संख्या है।

प्रश्न 7.
संख्या 40, 36 और 126 का अभाज्य गुणनखंडन विधि द्वारा HCF और LCM ज्ञात कीजिए ।
हल :

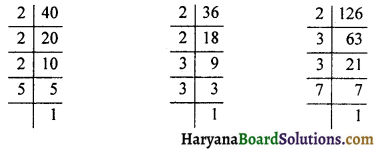
40 = 2 × 2 × 2 × 5 = 2³ × 5
36 = 2 × 2 × 3 × 3 = 2² × 3²
126 = 2 × 3 × 3 × 7 = 2 × 3² × 7
∴ HCF(40, 36, 126) = अभाज्य गुणनखंडों की उभयनिष्ठ सबसे छोटी घातों का गुणनफल = 2 उत्तर
LCM(40, 36, 126) = अभाज्य गुणनखंडों की सबसे बड़ी घातों का गुणनफल = 2³ × 3² × 5 × 7
= 8 × 9 × 5 × 7 = 2520

प्रश्न 8.
छः अंकों की सबसे बड़ी संख्या ज्ञात कीजिए जो 24, 15 तथा 36 से पूर्णतया विभाज्य हो ।
हल :
यहाँ पर हम पहले 24, 15 व 36 का LCM ज्ञात करेंगे।

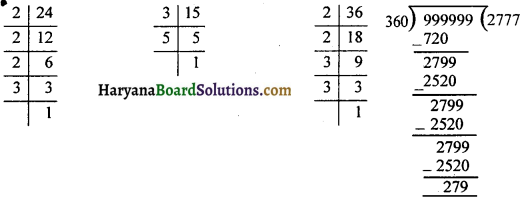
24 = 2 × 2 × 2 × 3 = 2³ × 3
15 = 3 × 5
36 = 2 × 2 × 3 × 3 = 2² × 3²
LCM(24, 15, 36) = 2³ × 3² × 5 = 8 × 9 × 5 = 360
हम जानते हैं कि छः अंकों की बड़ी से बड़ी संख्या = 999999
अतः अभीष्ट संख्या = 999999 – 279 = 999720

प्रश्न 9.
यदि दो संख्याओं का LCM व HCF क्रमशः 180 व 6 हो तथा इनमें से एक संख्या 30 हो तो दूसरी संख्या ज्ञात कीजिए ।
हल :
यहाँ पर,
LCM = 180
HCF = 6
पहली संख्या = 30
∴ दूसरी संख्या = LCM × HCF / पहली संख्या
= \(\frac{180 \times 6}{30}\)
= 6 × 6 = 36

प्रश्न 10.
वह बड़े से बड़े धनात्मक पूर्णांक ज्ञात कीजिए जो 398, 436 और 542 को विभाजित करने पर क्रमशः 7, 11 व 15 शेषफल छोड़े?
हल :
यहाँ पर

अब हम 391, 425 व 527 का HCF ज्ञात करेंगे-

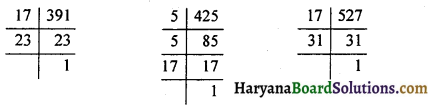
391 = 17 × 23
425 = 5 × 5 × 17 = 5² × 17
527 = 17 × 31
HCF (391, 425, 527) = 17
अतः वांछित पूर्णांक = 17

प्रश्न 11.
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय है-
(i) 3 – 2\(\sqrt{5}\)
(ii) 2\(\sqrt{3}\)
हल :
(i) माना 3 – 2\(\sqrt{5}\) एक परिमेय संख्या है जो कि दिए गए के विपरीत है ।
अब 3 – 2\(\sqrt{5}\) = \(\frac {a}{b}\) जहाँ a और b सह-अभाज्य पूर्णांक हैं तथा b ≠ 0 है।
⇒ 2\(\sqrt{5}\) = 3 – \(\frac {a}{b}\)
या 2\(\sqrt{5}\) = \(\frac{3 b-a}{b}\)
या \(\sqrt{5}\) = \(\frac{3 b-a}{2 b}\)
क्योंकि a और b पूर्णांक हैं जिस कारण \(\frac{3 b-a}{2b}\) एक परिमेय संख्या होगी ।
इसलिए \(\sqrt{5}\) एक परिमेय संख्या होगी जो कि असत्य है क्योंकि \(\sqrt{5}\) एक अपरिमेय संख्या है।
अतः हमारी कल्पना गलत है। इससे सिद्ध होता है कि 3 – 2\(\sqrt{5}\) एक अपरिमेय संख्या है।

(ii) यदि संभव हो तो माना 2\(\sqrt{3}\) एक परिमेय संख्या है।
तो 2\(\sqrt{3}\) = \(\frac {a}{b}\) जहाँ a और b सह-अभाज्य पूर्णांक हैं तथा b ≠ 0 है।
⇒ \(\sqrt{3}\) = \(\frac {a}{2b}\)
क्योंकि a और b पूर्णांक हैं जिस कारण \(\frac {a}{2b}\) एक परिमेय संख्या होगी ।
⇒ \(\sqrt{3}\) एक परिमेय संख्या होगी जो कि असत्य है क्योंकि \(\sqrt{3}\) एक अपरिमेय संख्या है।
अतः हमारी कल्पना गलत है। इससे सिद्ध होता है कि 2\(\sqrt{3}\) एक अपरिमेय संख्या है।

प्रश्न 12.
सिद्ध कीजिए कि \(\sqrt{3}\) एक अपरिमेय संख्या है।
हल :
माना \(\sqrt{3}\) एक परिमेय संख्या है जो कि दिए गए के विपरीत है ।
अब \(\sqrt{3}\) = \(\frac {a}{b}\) जहाँ a और b सह-अभाज्य पूर्णांक हैं तथा b ≠ 0 है ।
⇒ \(\sqrt{3}\)b = a
दोनों ओर का वर्ग करने पर,
3b² = a² ………..(i)
इससे पता चलता है कि a², 3 से विभाज्य है, इसलिए a भी 3 से विभाज्य होगी। …………..(ii)
⇒ a = 3m जहाँ m एक पूर्णांक है।
a का मान समीकरण (i) में रखने पर,
3b² = (3m)²
⇒ 3b² = 9m²
या b² = 3m²
इसका अर्थ यह है कि 3 से b² विभाजित हो जाता है इसलिए b भी 3 से विभाजित होगा । …………..(iii)
इसी प्रकार समीकरण (ii) व (iii) से a और b में कम-से-कम एक उभयनिष्ठ गुणनखंड 3 है। इससे हमारी कल्पना गलत होती है कि a और b सह-अभाज्य हैं । जिस कारण \(\sqrt{3}\) एक परिमेय संख्या नहीं है ।
अतः \(\sqrt{3}\) एक अपरिमेय संख्या है।

प्रश्न 13.
सिद्ध कीजिए कि 3\(\sqrt{2}\) एक अपरिमेय संख्या है।
हल :
यदि सम्भव हो तो माना 3\(\sqrt{2}\) एक परिमेय संख्या है।
तो 3\(\sqrt{2}\) = \(\frac {a}{b}\) जहाँ a और b सह – अभाज्य पूर्णांक हैं तथा b ≠ 0 है।
⇒ \(\sqrt{2}\) = \(\frac {a}{3b}\)
क्योंकि a और b पूर्णांक हैं जिस कारण \(\frac {a}{3b}\) एक परिमेय संख्या होगी ।
⇒ \(\sqrt{2}\) एक परिमेय संख्या होगी जोकि असत्य है क्योंकि \(\sqrt{2}\) एक अपरिमेय संख्या है।
अतः हमारी कल्पना गलत है। इससे सिद्ध होता है कि 3\(\sqrt{2}\) एक अपरिमेय संख्या है।

प्रश्न 14.
\(\frac {7}{160}\) का दशमलव प्रसार लिखिए ।
हल :

प्रश्न 15.
परिमेय संख्या 34.12345 के हर के अभाज्य गुणनखंडों के विषय में आप क्या कह सकते हैं?
हल :
क्योंकि 34.12345 एक सांत दशमलव संख्या है। इसलिए इस हर के अभाज्य गुणनखंडन 2ⁿ × 5^m के रूप के होंगे, जहाँ n और m पूर्णांक होंगे।

बहुविकल्पीय – प्रश्न :

प्रश्न 1.
निम्नलिखित में से कौन-सी संख्या अपरिमेय नहीं है?
(A) \(\sqrt{2}\)
(B) \(\sqrt{3}\)
(C) \(\sqrt{4}\)
(D) \(\sqrt{5}\)
हल :
(C) \(\sqrt{4}\)

प्रश्न 2.
प्रत्येक भाज्य संख्या को एक अद्वितीय रूप से …………….. संख्याओं के गुणनफल के रूप में व्यक्त किया जा सकता है ।
(A) अभाज्य
(B) सम
(C) विषम
(D) भाज्य
हल :
(A) अभाज्य

प्रश्न 3.
यूक्लिड विभाजन प्रमेयिका a = bq + का प्रयोग 17 व 6 के लिए करने पर का मान होगा-
(A) 6
(B) 2
(C) 17
(D) 5
हल :
(D) 5

प्रश्न 4.
यूक्लिड विभाजन प्रमेयिका a = bq + r का प्रयोग 20 व 4 के लिए करने पर का मान होगा-
(A) 5
(B) शून्य
(C) 4
(D) 20
हल :
(B) शून्य

प्रश्न 5.
12 व 5 का HCF क्या होगा ?
(A) 5
(B) 12
(C) 1
(D) 60
हल :
(C) 1

प्रश्न 6.
किन्हीं दो अभाज्य संख्याओं का HCF क्या होगा ?
(A) दोनों संख्याओं का गुणनफल
(B) बड़ी संख्या
(C) छोटी संख्या
(D) एक
हल :
(D) एक

प्रश्न 7.
20 व 5 का HCF क्या होगा ?
(A) 1
(B) 5
(C) 20
(D) 4
हल :
(B) 5

प्रश्न 8.
10 व 3 को यूक्लिड विभाजन प्रमेयिका के रूप में लिखा जा सकता है-
(A) 10 = 3 × 3 – 1
(B) 10 = 3 × 3 + 1
(C) 10 = 3 × 1 + 7
(D) 3 = 10 × 3 + 1
हल :
(B) 10 = 3 × 3 + 1

प्रश्न 9.
4 व 19 का HCF क्या होगा ?
(A) 4
(B) 19
(C) 1
(D) 76
हल :
(C) 1

प्रश्न 10.
510 व 92 का HCF क्या होगा ?
(A) 2
(B) 81
(C) 27
(D) 243
हल :
(A) 2

प्रश्न 11.
दो धनात्मक पूर्णांकों के LCM और HCF में सम्बन्ध होगा-
(A) HCF > LCM
(B) HCF = LCM
(C) LCM > HCF
(D) इनमें से कोई नहीं
हल :
(B) HCF = LCM (यदि धनात्मक पूर्णांक समान हों) तथा (C) LCM > HCF (यदि धनात्मक पूर्णांक भिन्न हों)

प्रश्न 12.
प्रत्येक धनात्मक विषम पूर्णांक को किस रूप में लिखा जा सकता है, जबकि p कोई पूर्णांक हो ?
(A) 2p+ 1
(B) 2p
(C) 2p + 2
(D) 4p
हल :
(A) 2p + 1

प्रश्न 13.
निम्नलिखित में से किस युग्म का HCF, 4 होगा ?
(A) 23, 4
(B) 28, 4
(C) 31, 4
(D) 10, 4
हल :
(B) 28, 4

प्रश्न 14.
निम्नलिखित में से किस युग्म का HCF, 4 नहीं होगा ?
(A) 12, 4
(B) 20, 4
(C) 22, 4
(D) 28, 4
हल :
(C) 22, 4

प्रश्न 15.
निम्नलिखित में से अपरिमेय (irrational) संख्या छाँटिए-
(A) \(\sqrt{36}\)
(B) \(\sqrt{121}\)
(C) \(\sqrt{9}\)
(D) \(\sqrt{8}\)
हल :
(D) \(\sqrt{8}\)

प्रश्न 16.
यदि 306 और 657 का HCF 9 हो, तो उसका LCM क्या होगा ?
(A) 2482
(B) 22338
(C) 2754
(D) 5913
हल :
(B) 22338

प्रश्न 17.
26 व 91 का HCF क्या होगा ?
(A) 26
(B) 867
(C) 13
(D) एक
हल :
(C) 13

प्रश्न 18.
1232 व 32 का HCF क्या होगा ?
(A) 16
(B) 616
(C) 8
(D) 2464
हल :
(A) 16

प्रश्न 19.
336 व 54 का HCF क्या होगा ?
(A) 9
(B) 3
(C) 6
(D) 18
हल :
(C) 6

प्रश्न 20.
यदि q कोई पूर्णांक हो तो एक धनात्मक विषम पूर्णांक को लिखा जा सकता है-
(A) 4q
(B) 4q + 1
(C) 4q + 2
(D) 4q + 4
हल :
(B) 4q + 1

प्रश्न 21.
यदि q कोई पूर्णांक हो तो एक धनात्मक विषम पूर्णांक को किस रूप में नहीं लिखा जा सकता?
(A) 6q +1
(B) 6q + 2
(C) 6q + 3
(D) 6q + 5
हल :
(B) 6q + 2

प्रश्न 22.
एक मिठाई विक्रेता के पास 420 काजू की बर्फियाँ और 130 बादाम की बर्फियाँ हैं। वह इनकी ऐसी ढेरियाँ बनाना चाहता है कि प्रत्येक ढेरी में बर्फियों की संख्या समान रहे तथा ये ढेरियाँ बर्फी की परात में न्यूनतम स्थान घेरें । इस काम के लिए, प्रत्येक ढेरी में कितनी बर्फियाँ रखी जा सकती हैं?
(A) 30
(B) 130
(C) 20
(D) 10
हल :
(D) 10

प्रश्न 23.
किसी परेड में 616 सदस्यों वाली एक सेना की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैंड के पीछे मार्च करना है। दोनों समूहों को समान संख्या वाले स्तंभों में मार्च करना है। उन स्तंभों की अधिकतम संख्या क्या होगी जिसमें वे मार्च कर सकते हैं?
(A) 8
(B) 32
(C) 4
(D) 2
हल :
(A) 8

प्रश्न 24.
प्रत्येक भाज्य संख्या को अभाज्य संख्याओं के एक गुणनफल के रूप में व्यक्त (गुणनखंडित) किया जा सकता है तथा यह गुणनखंडन अद्वितीय होता है, इस पर कोई ध्यान दिए बिना कि अभाज्य गुणनखंड किस क्रम में आ रहे हैं। इसे कहा जाता है-
(A) यूक्लिड विभाजन प्रमेय
(B) अंकगणित की आधारभूत प्रमेय
(C) बीजगणित की आधारभूत प्रमेय
(D) रेखागणित की आधारभूत प्रमेय
हल :
(B) अंकगणित की आधारभूत प्रमेय

प्रश्न 25.
सबसे छोटी अभाज्य संख्या है-
(A) 2
(B) 3
(C) 1
(D) 5
हल :
(A) 2

प्रश्न 26.
सबसे छोटी विषम अभाज्य संख्या है-
(A) 1
(B) 2
(C) 3
(D) 5
हल :
(C) 3

प्रश्न 27.
30 के अभाज्य गुणनखंड होंगे-
(A) 6 × 5
(B) 1 × 30
(C) 2 × 15
(D) 2 × 3 × 5
हल :
(D) 2 × 3 × 5

प्रश्न 28.
दो पूर्णांकों 336 तथा 54 का LCM होगा-
(A) 12
(B) 3024
(C) 6
(D) इनमें से कोई नहीं
हल :
(B) 3024

प्रश्न 29.
72 के अभाज्य गुणनखंड होंगे-
(A) 2³ × 3³
(B) 2³ × 3³
(C) 2³ × 3³
(D) 2³ × 3²
हल :
(D) 2³ × 3²

प्रश्न 30.
यदि 96 और 404 का HCF 4 हो तो उनका LCM होगा-
(A) 38784
(B) 9696
(C) 2274
(D) इनमें से कोई नहीं
हल :
(B) 9696

प्रश्न 31.
140 के अभाज्य गुणनखंड होंगे-
(A) 2² × 5² × 7²
(B) 2² × 5² × 7
(C) 2² × 5 × 7
(D) 2 × 5 × 7
हल :
(C) 2² × 5 × 7

प्रश्न 32.
156 के अभाज्य गुणनखंड होंगे-
(A) 2² × 3 × 13
(B) 2² × 3² × 13
(C) 2² × 3² × 13²
(D) 2 × 3² × 13
हल :
(A) 2² × 3 × 13

प्रश्न 33.
12 और 20 के HCF और LCM में सम्बन्ध होगा-
(A) HCF > LCM
(B) HCF < LCM
(C) HCF = LCM
(D) इनमें से कोई नहीं
हल :
(B) HCF < LCM

प्रश्न 34.
6, 72 व 120 का LCM होगा-
(A) 240
(B) 360
(C) 120
(D) 152
हल :
(B) 360

प्रश्न 35.
12, 15 व 21 का LCM होगा-
(A) 420
(B) 315
(C) 410
(D) इनमें से कोई नहीं
हल :
(A) 420

प्रश्न 36.
किन्हीं तीन विभिन्न अभाज्य संख्याओं का HCF होगा-
(A) तीनों संख्याओं का गुणनफल
(B) सबसे छोटी संख्या
(C) सबसे बड़ी संख्या
(D) एक
हल :
(D) एक

प्रश्न 37.
किन्हीं तीन विभिन्न अभाज्य संख्याओं का LCM होगा-
(A) सबसे छोटी संख्या
(B) सबसे बड़ी संख्या
(C) तीनों संख्याओं का गुणनफल
(D) एक
हल :
(C) तीनों संख्याओं का गुणनफल .

प्रश्न 38.
17, 23 व 29 का LCM होगा-
(A) 1140
(B) 1139
(C) 1239
(D) इनमें से कोई नहीं
हल :
(D) इनमें से कोई नहीं

प्रश्न 39.
510 व 92 का LCM होगा-
(A) 23460
(B) 3460
(C) 2346
(D) 1800
हल :
(A) 23460

प्रश्न 40.
पूर्णांक 8, 9 और 25 का LCM है-
(A) 1500
(B) 1700
(C) 1800
(D) इनमें से कोई नहीं
हल :
(C) 1800

प्रश्न 41.
यदि 36 व x का HCF व LCM क्रमशः 6 व 180 हो तो x का मान होगा-
(A) 180
(B) 36
(C) 30
(D) 6
हल :
(C) 30

प्रश्न 42.
यदि दो संख्याओं का गुणनफल 240 तथा उनका HCF 4 हो तो LCM होगा-
(A) 12
(B) 20
(C) 240
(D) 60
हल :
(D) 60

प्रश्न 43.
यदि दो संख्याओं का HCF व LCM क्रमशः 24 व 360 हो तथा इनमें से एक संख्या 72 हो तो दूसरी संख्या होगी-
(A) 120
(B) 60
(C) 30
(D) 15
हल :
(A) 120

प्रश्न 44.
किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारंभ करके एक ही दिशा में चलते हैं। कितने समय बाद वे पुनः प्रारंभिक स्थान पर मिलेंगे?
(A) 6 मिनट
(B) 12 मिनट
(C) 18 मिनट
(D) 36 मिनट
हल :
(D) 36 मिनट

प्रश्न 45.
किसी स्कूल की नौवीं कक्षा के सैक्शन-ए में 36 विद्यार्थी तथा सैक्शन -बी में 32 विद्यार्थी हैं । इस स्कूल की लाइब्रेरी में कम से कम कितनी किताबें होनी चाहिएँ ताकि सैक्शन-ए या सैक्शन-बी के विद्यार्थियों को बराबर-बराबर दी जा सके ?
(A) 144
(B) 288
(C) 32
(D) 36
हल :
(B) 288

प्रश्न 46.
\(\sqrt{5}\) हैं :
(A) सम
(B) विषम
(C) परिमेय
(D) अपरिमेय
हल :
(D) अपरिमेय

प्रश्न 47.
………………… और अपरिमेय संख्याएँ मिलकर वास्तविक संख्याएँ बनाती हैं?
(A) परिमेय
(B) सम
(C) विषम
(D) अभाज्य
हल :
(A) परिमेय

प्रश्न 48.
\(\sqrt{3}\) है :
(A) परिमेय
(B) अपरिमेय
(C) मिश्रित संख्या
(D) इनमें से कोई नहीं
हल :
(B) अपरिमेय

प्रश्न 49.
निम्नलिखित में से कौन-सी संख्या अपरिमेय नहीं है?
(A) \(\sqrt{2}\)
(B) \(\sqrt{3}\)
(C) \(\sqrt{13}\)
(D) \(\sqrt{16}\)
हल :
(D) \(\sqrt{16}\)

प्रश्न 50.
\(\sqrt{2}\) है-
(A) अपरिमेय
(B) परिमेय
(C) मिश्रित संख्या
(D) इनमें से कोई नहीं
हल :
(A) अपरिमेय

प्रश्न 51.
यदि \(\frac {p}{q}\) एक ऐसी परिमेय संख्या हो, जिसमें q = 2ⁿ5^m जहाँ n और m ऋणेतर पूर्णांक है तो इसका दशमलव प्रसार होगा-
(A) असांत आवर्ती
(B) असांत अनावर्ती
(C) सांत
(D) असांत
हल :
(C) सांत

प्रश्न 52.
निम्नलिखित में से किस संख्या का दशमलव प्रसार असांत आवर्ती होगा ?
(A) \(\frac{3}{2^3}\)
(B) \(\frac{13}{5^3}\)
(C) \(\frac{23}{2^3 5^2}\)
(D) \(\frac{129}{2^2 5^7 7^5}\)
हल :
(D) \(\frac{129}{2^2 5^7 7^5}\)

प्रश्न 53.
निम्नलिखित में से किस संख्या का दशमलव प्रसार सांत होगा-
(A) \(\frac{29}{7^3}\)
(B) \(\frac{2}{5^1}\)
(C) \(\frac{11}{3^1 5^1 7^1}\)
(D) \(\frac{13}{2^3 7^3}\)
हल :
(B) \(\frac{2}{5^1}\)

प्रश्न 54.
निम्नलिखित में से किस संख्या का दशमलव प्रसार असांत आवर्ती होगा ?
(A) \(\frac {3}{8}\)
(B) \(\frac {13}{125}\)
(C) \(\frac {17}{9}\)
(D) \(\frac {7}{80}\)
हल :
(C) \(\frac {17}{9}\)

प्रश्न 55.
\(\frac {3}{8}\) का दशमलव प्रसार होगा-
(A) 0.375
(B) 0.0375
(C) 3.75
(D) 0.00375
हल :
(A) 0.375

प्रश्न 56.
निम्नलिखित में से अपरिमेय (irrational) संख्या छाँटिए-
(A) \(\sqrt{9}\)
(B) \(\sqrt{14}\)
(C) \(\sqrt{25}\)
(D) \(\sqrt{36}\)
हल :
(B) \(\sqrt{14}\)

प्रश्न 57.
यदि 124 और 148 का HCF 4 हो, तो उसका LCM क्या होगा ?
(A) 1147
(B) 18352
(C) 4588
(D) इनमें से कोई नहीं
हल :
(C) 4588

प्रश्न 58.
\(\frac {17}{8}\) का दशमलव प्रसार होगा-
(A) 0.2125
(B) 0.02125
(C) 2.125
(D) 21.25
हल :
(C) 2.125

प्रश्न 59.
निम्नलिखित में से अपरिमेय (irrational) संख्या छाँटिए-
(A) \(\sqrt{8}\)
(B) \(\sqrt{16}\)
(C) \(\sqrt{49}\)
(D) \(\sqrt{81}\)
हल :
(A) \(\sqrt{8}\)

प्रश्न 60.
यदि 135 और 225 का HCF 45 हो, तो उसका LCM क्या होगा ?
(A) 405
(B) 1125
(C) 675
(D) इनमें से कोई नहीं
हल :
(C) 675