Haryana State Board HBSE 9th Class Maths Solutions Chapter 7 त्रिभुज Ex 7.2 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 7 त्रिभुज Exercise 7.2
प्रश्न 1.
एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेद करते हैं। A और O को जोड़िए। दर्शाइए कि
(i) OB = OC
(ii) AO कोण A को समद्विभाजित करता है।
हल :
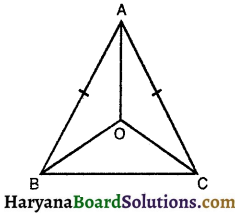
(i) यहाँ पर ΔABC में,
AB = AC
∠B = ∠C [समान भुजाओं के सम्मुख कोण]
या \(\frac {1}{2}\)∠B = \(\frac {1}{2}\)∠C
या ∠OBC = ∠OCB …….(i) [∵ OB तथा OC क्रमशः ∠B तथा ∠C के समद्विभाजक हैं] ….(ii)
⇒ OB = OC [समान कोणों की सम्मुख भुजाएँ] [इति सिद्धम]
(ii) अब ΔABO तथा ΔACO में,
AB = AC [दिया है]
∠OBA = ∠OCA [समान कोणों के समद्विभाजक]
OB = OC [प्रमाणित]
ΔABO ≅ ΔACO [भुजा-कोण-भुजा सर्वांगसमता]
∠BAO = ∠CAO [सर्वांगसम त्रिभुजों के संगत भाग]
AO, ∠BAC को समद्विभाजित करता है। [इति सिद्धम]
![]()
प्रश्न 2.
ΔABC में AD भुजा BC का लंब समद्विभाजक है (देखिए आकृति)। दर्शाइए कि ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
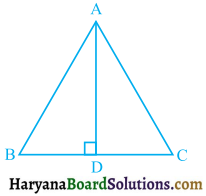
हल :
ΔABD और ΔACD में,
DB = DC [दिया है]
∠ADB = ∠ADC [∵ AD ⊥ BC]
AD = AD [उभयनिष्ठ]
⇒ ΔABD ≅ ΔACD [भुजा-कोण-भुजा सर्वांगसमता]
अतः AB = AC [सर्वागसम त्रिभुजों के संगत भाग]
इसलिए ΔABC एक समद्विबाहु त्रिभुज है। [इति सिद्धम]
प्रश्न 3.
ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमशः शीर्षलंब BE और CF खींचे गए हैं (देखिए आकृति)। दर्शाइए कि ये शीर्षलंब बराबर हैं।
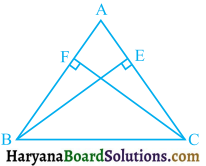
हल :
यहाँ पर दिया है BE ⊥ AC तथा CF ⊥ AB
ΔABE और ΔACF में,
∠AEB = ∠AFC [प्रत्येक = 90°]
∠A = ∠A [उभयनिष्ठ]
AB = AC [दिया है]
∴ ΔABE ≅ ΔACF [कोण-कोण-भुजा सर्वांगसमता]
या BE = CF [∵ सर्वागसम त्रिभुजों के संगत भाग]
अतः दिए गए शीर्षलंब बराबर हैं। [इति सिद्धम]
![]()
प्रश्न 4.
ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलंब BE और CF बराबर हैं (देखिए आकृति)। दर्शाइए कि
(i) ΔABE ≅ ΔACF
(ii) AB = AC अर्थात् ΔABC एक समद्विबाहु त्रिभुज है।
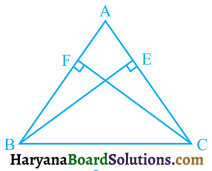
हल :
(i) ΔABE तथा ΔACF में,
∠AEB = ∠AFC [प्रत्येक = 90°]
∠BAE = ∠CAF [उभयनिष्ठ]
BE = CF [दिया है]
∴ ΔABE ≅ ΔACF [कोण-कोण-भुजा सर्वांगसमता] [इति सिद्धम]
(ii) AB = AC
[∵ सर्वांगसम त्रिभुजों के संगत भाग]
अतः ΔABC एक समद्विबाहु त्रिभुज है। [इति सिद्धम]
प्रश्न 5.
ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं (देखिए आकृति)। दर्शाइए कि ∠ABD = ∠ACD है।
हल :
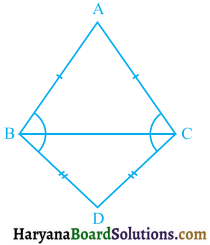
यहाँ पर ΔABC में,
AB = AC [दिया है]
⇒ ∠ABC = ∠ACB [समान भुजाओं के सम्मुख कोण] …(i)
इसी प्रकार ΔBCD में,
BD = CD [दिया है]
∴ ∠DBC = ∠DCB [समान भुजाओं के सम्मुख कोण] …(ii)
समीकरण (i) व (ii) से,
∠ABC + ∠DBC = ∠ACB + ∠DCB
या ∠ABD = ∠ACD [इति सिद्धम]
![]()
प्रश्न 6.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिंदु D तक इस प्रकार बढ़ाई गई है कि AD = AB है (देखिए आकृति)। दर्शाइए कि ∠BCD एक समकोण है।
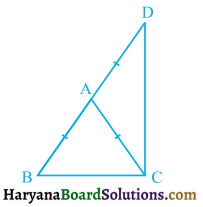
हल :
यहाँ पर ΔABC में,
AB = AC [दिया है]
∠ACB = ∠ABC ………..(i)
[समान भुजाओं के सम्मुख कोण]
परंतु AB = AD [दिया है]
⇒ AD = AC [∵ AB = AC]
इसीलिए ΔADC में, AD = AC
⇒ ∠ACD = ∠ADC …(ii) [समान भुजाओं के सम्मुख कोण]
समीकरण (i) व (ii) से,
∠ACB + ∠ACD = ∠ABC + ∠ADC
या ∠BCD = ∠ABC + ∠BDC
[∵ ∠ADC = ∠BDC]
दोनों ओर ∠BCD जोड़ने पर,
∠BCD + ∠BCD = ∠ABC + ∠BDC + ∠BCD
या 2∠BCD = 180° [त्रिभुजों के कोणों का योगफल]
या ∠BCD = 90°
अतः ∠BCD एक समकोण है। [इति सिद्धम]
प्रश्न 7.
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
हल :
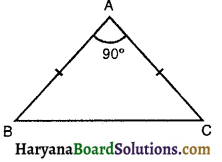
ΔABC में,
∠A = 90°
AB = AC
⇒ ∠B = ∠C [समान भुजाओं के सम्मुख कोण]
हम जानते हैं कि, ∠A + ∠B + ∠C = 180°
या 90° + 2∠B = 180° [∵ ∠C = ∠B]
या 2∠B = 180° – 90° = 90°
या ∠B = \(\frac {90°}{2}\) = 45°
अतः ∠C = ∠B = 45° उत्तर
![]()
प्रश्न 8.
दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है। (B.S.E.H. March, 2018)
हल :
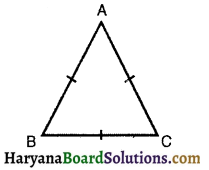
माना ΔABC एक समबाहु त्रिभुज है। अतः AB = AC = BC
अब क्योंकि
AB = AC
∠B = ∠C ………..(i) [समान भुजाओं के सम्मुख कोण]
इसी प्रकार,
CB = CA
⇒ ∠A = ∠B ……….(ii) [समान भुजाओं के सम्मुख कोण]
समीकरण (i) व (ii) से,
हम जानते हैं कि,
∠A + ∠B + ∠ C = 180°
या ∠A + ∠A + ∠A = 180°
या 3∠A = 180° या ∠A = 60°
∴ ∠A = ∠B = ∠C = 60°
अतः समबाहु त्रिभुज का प्रत्येक कोण 60 होता है। [इति सिद्धम]