Haryana State Board HBSE 9th Class Maths Solutions Chapter 4 Linear Equations in Two Variables Ex 4.4 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 4 Linear Equations in Two Variables Exercise 4.4
Question 1.
Give the geometric representations of y = 3 as an equation :
(i) in one variable
(ii) in two variables.
Solution :
(i) The representation of the solution on the number line is shown in figure 4.26, where y = 3 is treated as an equation in one variable.

(ii) We know that y = 3 can be written as 0.x + 1.y = 3 which is a linear equation in two variables x and y. This is represented by a line. Now all the values of x are permissible because 0.x is always 0. However y must satisfy the equation y = 3.
Hence, three solutions of the given equation are x = 0, y = 3; x = – 2, y = 3 and x = 3, y = 3.

Plotting the points A(- 2, 3), B(0, 3) and C(3, 3) on the graph paper and joining these points, we get a straight line AC. It is a graph of a line y = 3. The graph of a line is parallel to x-axis at a distance of 3 units above it.
![]()
Question 2.
Give the geometric representations of 2x + 9 = 0 as an equation :
(i) in one variable
(ii) in two variables.
Solution :
(i) The representation of the solution of the equation 2x + 9 = 0 i.e., x = \(\frac {- 9}{2}\) on the number line is shown in the figure 4.28, where x = \(\frac {- 9}{2}\) is treated as an equation in one variable
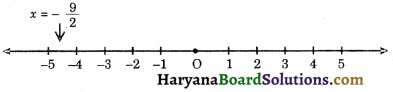
(ii) We know that 2x + 9 = 0 can be written as 2x + 0.y + 9 = 0 as a linear equation in two variables x and y. Now all the values of y are permissible because 0.y is always zero. However, x must satisfy the equation 2x + 9 = 0 i.e., x = \(\frac {- 9}{2}\)
Hence, three solutions of the given equation are \(\frac {- 9}{2}\), 3; \(\frac {- 9}{2}\), 0; \(\frac {- 9}{2}\), – 2.

Plotting the points A(\(\frac {- 9}{2}\), 3), B(\(\frac {- 9}{2}\), 0) and C(\(\frac {- 9}{2}\), – 2) on the graph paper and joining these points, we get a straight line AC. It is the required graph of equation 2x + 9 = 0. The graph of a equation is parallel to y-axis at a distance of \(\frac {9}{2}\)units on left of y-axis.