Haryana State Board HBSE 9th Class Maths Solutions Chapter 4 Linear Equations in Two Variables Ex 4.3 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 4 Linear Equations in Two Variables Exercise 4.3
Question 1.
Draw the graph of each of the following linear equations in two variables :
(i) x + y = 4
(ii) x – y = 2
(iii) y = 3x
(iv) 3 = 2x + y
Solution:
(i) We have,
x + y = 4
⇒ y = 4 – x
When x = 0, then y = 4 – 0 = 4
When x = 1, then y = 4 – 1 = 3
When x = 2, then y = 4 – 2 = 2
Now, we prepare the table of values of (x, y).
| x | 0 | 1 | 2 |
| y | 4 | 3 | 2 |
Plotting the points A(0, 4), B(1, 3) and C(2, 2) on the graph paper and joining these points, we get a straight line AC. It is the required graph of x + y = 4.

(ii) We have,
x – y = 2
⇒ – y = – x + 2
⇒ y = x – 2
When x = 0, then y = 0 – 2 = – 2
When x = 2, then y = 2 – 2 = 0
When x = 4, then y = 4 – 2 = 2
Now, we prepare the table of values of (x, y).
| x | 0 | 2 | 4 |
| y | – 2 | 0 | 2 |
Plotting the points A(0, – 2), B(2, 0) and C(4, 2) on the graph paper and joining these points, we get a straight line AC. It is the required graph of x – y = 2.

(iii) We have, y = 3x
When x = 0, then y = 0
When x = 1, then y = 3 × 1 = 3
When x = 2, then y = 3 × 2 = 6
Now, we prepare the table of values of (x, y).
| x | 0 | 1 | 2 |
| y | 0 | 3 | 6 |
Plotting the points A(0, 0), B(1, 3) and C(2, 6) on the graph paper and joining these points, we get a straight line AC. It is the required graph of y = 3x.

(iv) We have,
3 = 2x + y
⇒ y = 3 – 2x
When x = 0, then y = 3 – 2 × 0 = 3 – 0 = 3
When x = 1, then y = 3 – 2 × 1 = 3 – 2 = 1
When x = 2, then y = 3 – 2 × 2 = 3 – 4 = – 1
Now, we prepare the table of values of (x, y)
| x | 0 | 1 | 2 |
| y | 3 | 1 | – 1 |
Plotting the points A(0, 3), B(1, 1) and C(2, – 1) on the paper and joining these points, we get a straight line AC. It is the required graph of 3 = 2x + y.
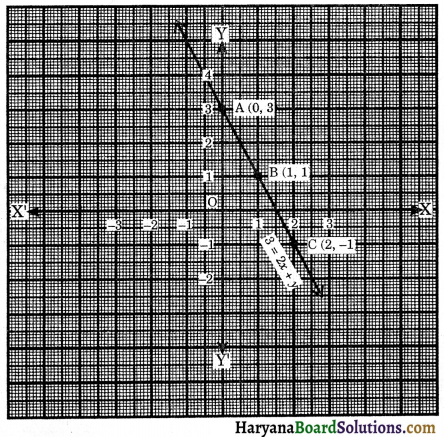
![]()
Question 2.
Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?
Solution:
Equations of two lines passing through (2, 14) are x + y = 16, 2x + y = 18. But note that, 8x – y = 2, 3x + y = 20 and 6x – y = – 2 are also satisfied by the co-ordinates of the point (2, 14). So, infinitely many number of lines can be pass through the point (2, 14).
Question 3.
If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.
Solution:
Since the point (3, 4) lies on the graph of the equation 3y = ax + 7. Therefore, the point (3, 4) satisfies the given equation.
⇒ 3 × 4 = a × 3 + 7
⇒ 12 = 3a + 7
⇒ 12 – 7 = 3a
⇒ 5 = 3a
⇒ a = \(\frac {5}{3}\)
Hence, a = \(\frac {5}{3}\)
![]()
Question 4.
The taxi fare in a city is as follows: For the first kilometre, the fare is ₹ 8 and for the subsequent distance it is ₹ 5 per km. Taking the distance covered as x km and total fare as ₹ y, write a linear equation for this information, and draw its graph.
Solution:
Taking the distance covered as x km and total fare as ₹ y.
Fare for first km = ₹ 8
Remaining distance = (x – 1) km
Fare for remaining distance = (x – 1) × 5
Total fare (y) for x km = 8 + (x – 1) × 5
⇒ y = 8 + (x – 1) × 5
⇒ y = 8 + 5x – 5
⇒ y = 5x + 3
When x = 1, then y = 5 × 1 + 3 = 5 + 3 = 8
When x = 2, then y = 5 × 2 + 3 = 10 + 3 = 13
When x = 3, then y = 5 × 3+ 3 = 15 + 3 = 18
Now, we prepare the table of values of (x, y).
| x | 1 | 2 | 3 |
| y | 8 | 13 | 18 |
Plotting the points A(1, 8), B(2, 13) and C(3, 18) on the graph paper and joining these points, we get a straight line AC. It is the required graph of y = 5x + 3.
Hence, linear equation is 5x – y + 3 = 0.

Question 5.
From the choices given below, choose the equation whose graphs are given in figure 4.15 and 4.16:
For figure 4.15
(i) y = x
(ii) x + y = 0
(iii) y = 2
(iv) 2 + 3y = 7x
(v) x + 2y = 6
For figure 4.16
(i) y = x + 2
(ii) y = x – 2
(iii) y = -x + 2

Solution:
For figure 4:15, the points on the line are (1, – 1), (0, 0) and (-1, 1). We observe that co-ordinates of the point of the graph satisfy the equation x + y = 0. So, x + y = 0 is the equation corresponding to the graph in figure 4:15.
So, the correct option is (ii) x + y = 0.
For figure 4:16, the points on the line are (2, 0), (0, 2) and (-1, 3). We observe that coordinates of the points of the graph satisfy the equation y = – x + 2. So, y = – x + 2 is the equation corresponding to the graph in figure 4.16.
So, the correct option is (iii) y = – x + 2.
![]()
Question 6.
If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is : (i) 2 units (ii) 0 unit.
Solution :
Let the work done by the body be y units and distance travelled by x units. According to question, work done by the body on application of a constant force is directly proportional to the distance travelled by the body. From ratio and proportion we can express this fact as:
y = 5x[∵ work done = force × distance]
Taking distance x along x-axis and work done along y-axis.
When x = 0, then y = 5 × 0 = 0
When x = 1, then y = 5 × 1= 5
When x = 2, then y = 5 × 2 = 10
When x = 3, then y = 5 × 3 = 15
Now, we prepare the table of values of (x, y).
| x | 0 | 1 | 2 | 3 |
| y | 0 | 5 | 10 | 15 |
Plotting the points A(0, 0), B(1, 5), C(2, 10) and D(3, 15) on the graph paper and joining these points, we get a straight line AD. It is the required graph of y = 5x.

From the graph we observe that:
(i) When distance (x) = 2 units, then work done (y) = 10 units.
(ii) When distance (x) = 0 unit, then work done (y) = 0 unit.
Question 7.
Yamini and Fatima, two students of class IX of a school, together contributed ₹ 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You may take their contributions as ₹ x and ₹ y). Draw the graph of the same.
Solution:
Let the contribution of Yamini be ₹ x and contribution of Fatima be ₹ y.
According to question, x + y = 100
⇒ y = 100 – x
When x = 10, then y = 100 – 10 = 90
When x = 20, then y = 100 – 20 = 80
When x = 30, then y = 100 – 30 = 70
When x = 40, then y = 100 – 40 = 60
Now, we prepare the table of values of (x, y).
| x | 10 | 20 | 30 | 40 |
| y | 90 | 80 | 70 | 60 |
Plotting the points A(10, 90), B(20, 80), C(30, 70) and D(40, 60) on the graph paper. Joining these points we get a straight line AD. It is the required graph of x + y = 100.

Hence, required linear equation is x + y = 100.
![]()
Question 8.
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius :
F = (\(\frac {9}{5}\)) C + 32
(i) Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis.
(ii) If the temperature is 30°C, what is the temperature in Fahrenheit?
(iii) If the temperature is 95°F, what is the temperature in Celsius?
(iv) If the temperature is 0°C, what is the temperature in Fahrenheit and if the temperature is O’F, what is the temperature in Celsius?
(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.
Solution:
We have,
F = \(\frac {9}{5}\)C + 32
Taking the temperature in Celsius along x-axis and temperature in Fahrenheit along y-axis.
When C = 20, then
F = \(\frac {9}{5}\) × 20 + 32
= 36 + 32 = 68
When C = 40, then
F = \(\frac {9}{5}\) × 40+32
= 72 + 32 = 104
When C = 60, then
F = \(\frac {9}{5}\) × 60 + 32
= 108 + 32 = 140
When C = – 40, then
F = \(\frac {9}{5}\) × (-40) + 32
= – 72 + 32 = – 40
Now, we prepare the table of values of (C, F).
| °C | 20 | 40 | 60 | – 40 |
| °F | 68 | 104 | 140 | – 40 |
Plotting the points A(20, 68), B(40, 104), C(60, 140) and D(-40, – 40) on the graph paper and joining these points, we get a straight line CD. It is the required graph of F = \(\frac {9}{5}\)C + 32.

(i) The graph is shown in the above figure.
(ii) If the temperature is 30°C, then temperature in Fahrenheit is 86°F.
(iii) If the temperature is 95°F, then temperature in Celsius is 35°C.
(iv) If the temperature is 0°C, then temperature in Fahrenheit is 32°F and if temperature is 0°F, then temperature in Celsius is – 17.8°C (approx.).
(v) Let 0°C = 0°F = x
Substituting the 0°C = 0°F = x in the equation, we get
x = \(\frac {9}{5}\)x + 32
x – \(\frac {9}{5}\)x = 32
\(\frac{5 x-9 x}{5}\) = 32
\(\frac{-4 x}{5}\) = 32
x = \(\frac{32 \times 5}{-4}\) = – 40
Yes, a temperature which is numerically the same in both Fahrenheit and Celsius is – 40, which is shown in the figure 4.19 at point D.