Haryana State Board HBSE 9th Class Maths Important Questions Chapter 7 Triangles Important Questions and Answers.
Haryana Board 9th Class Maths Important Questions Chapter 7 Triangles
Very Short Answer Type Questions
Question 1.
In ΔPQR, if altitude PM bisects QR, prove that PQ = PR.
Solution :
Given: A ΔPQR such that PM ⊥ QR and MQ = MR.
To prove PQ = PR.
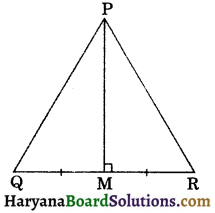
Proof: In ΔPMQ and ΔPMR, we have
MQ = MR, (Given)
∠PMQ = ∠PMR, (Each = 90°)
and PM = PM, (Common)
∴ ΔPMQ ≅ ΔPMR,
(By SAS congruence rule)
⇒ PQ = PR (CPCT)
Hence Proved
![]()
Question 2.
In the figure, BD ⊥ AC, CE ⊥ AB and AB = AC. Prove that BD = CE.
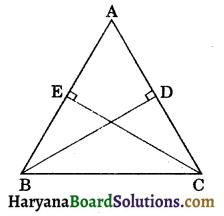
Solution :
In ΔABD and ΔACE, we have
∠ADB = ∠AEC (Each = 90°)
∠BAD = ∠CAE (Common)
and AB = AC (Given)
∴ ΔABD ≅ ΔACE
(By AAS congruence rule)
⇒ BD = CE (CPCT)
Hence Proved
Question 3.
In the figure, ABCD is a quadrilateral in which AX ⊥ BD, CY ⊥ BD, AX = CY and BX = YD. Show that :
(i) ΔAXD ≅ ΔCYB
(ii) AD = BC.
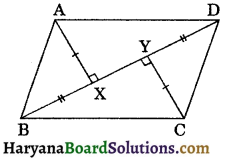
Solution :
(i) We have
BX = YD
⇒ BX + XY = YD + XY,
(Adding XY on both sides)
⇒ BY = XD ……(i)
Now in ΔAXD and ΔCYB, we have
AX = CY. (Given)
∠AXD = ∠CYB (Each = 90°)
and XD = BY, [From (i)]
∴ ΔAXD ≅ ΔCYB, (By SAS congruence rule)
⇒ AD = BC,
Hence proved
(ii) ΔАХD ≅ ΔCYB (As proved above)
⇒ AD = BC, (CPCT)
Hence proved
Question 4.
On the arms AB and BC of an ∠ABC, points N and M are taken respectively such that ∠MAB = ∠NCB (see the figure). If AB = BC, then prove that BM = BN.
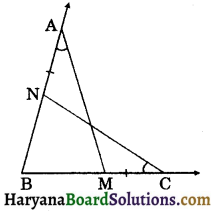
Solution :
In ΔABM and ΔCBN, we have
∠MAB = ∠NCB, (Given)
AB = BC, (Given)
∠B = ∠B (Common)
∴ ΔABM ≅ ΔCBN,
(By ASA congruence rule)
⇒ BM = BN, (CPCT)
Hence proved
![]()
Question 5.
In the figure, AP ⊥ BD, CQ ⊥ BD and AP = CQ. Prove that BD bisects AC.
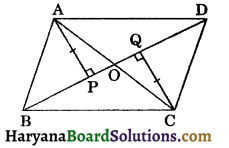
Solution :
In ΔAOP and ΔCOQ, we have
∠APO = ∠CQO,
[∵ AP ⊥ BD and CQ ⊥ BD
∴ Each = 90°]
∠AOP = ∠COQ,
(Vertically opposite angles) and
and AP = CQ, (Given)
∴ ΔAOP ≅ ΔCOQ,
(By AAS congruence rule)
⇒ AO = OC, (CPCT)
⇒ O is the midpoint of AC.
Hence, BD bisects AC. Hence Proved
Question 6.
See figure, explain how one can find the breadth of the river without crossing it.
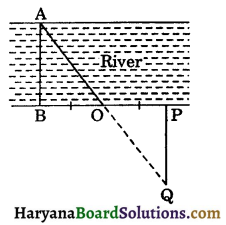
Solution :
AB be the breadth of river Mark Point P on the bank of river.
Construction: Let O be the midpoint of BP. Mark a point Q on AO produced such that AO = OQ. Join PQ.
Now in ΔAOB and ΔQOP, we have
BO = OP
(O is the midpoint of BP)
∠AOB = ∠QOP
(Vertically opposite angles)
and AO = OQ (By construction)
∴ ΔAOB ≅ ΔQOP
(By SAS congruence rule)
⇒ AB = PQ (CPCT)
Hence, breadth of river AB = PQ i.e., one should measure PQ to find the breadth AB of the river.
Question 7.
In the figure, AP is the bisector of ∠CAD and AP || BC. Prove that AB = AC.
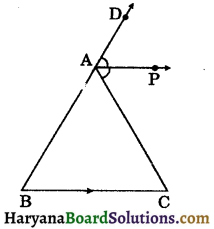
Solution :
∠DAP = ∠CAP …………..(i)
(∵ AP is the bisector of ∠CAD)
∵ AP || ВC (Given)
∠DAP = ∠ABC …………..(ii)
(Corresponding angles)
∠CAP = ∠ACB ………….(iii)
(Alternate interior angles)
From (i), (ii) and (iii), we get
∠ABC = ∠ACB
⇒ AB = AC, (sides opposite to equal angles are equal)
Hence proved
![]()
Question 8.
In the figure, AC = BC and ∠x = ∠y.
Prove that: (i) ΔABD ≅ ΔBAE (ii) AD = BE.
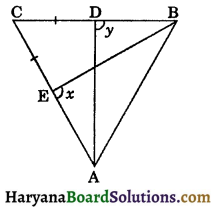
Solution :
(i) We have, BC = AC, (Given)
⇒ ∠B = ∠A, …………(i)
(Angles opposite to equal sides are equal)
In ΔABD and ΔBAE, we have
∠B = ∠A [from (i)]
∠y = ∠x, (Given)
and AB = AB, (Common)
∴ ΔABD ≅ ΔBAE, (By AAS congruence rule)
Hence proved
(ii) ΔABD ≅ ΔBAE (CPCT)
AD = BE. Hence proved
Question 9.
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
[NCERT Exemplar Problems]

Solution :
In ΔABD and ΔCBD, we have
AB = BC (given)
AD = CD (given)
and BD = BD (common)
∴ ΔABD = ΔCBD
(by SSS congruence rule)
⇒ ∠ABD = ∠CBD (CPCT) and
and ∠ADB = ∠CDB (CPCT)
So, BD bisects ∠ABC and ∠ADC.
Hence proved
![]()
Question 10.
In a triangle ABC, if ∠A = 55° and ∠C = 65°. Determine the shortest and longest sides of the triangle.
Solution :
In a ΔABC, we have
∠A = 55°, ∠C = 65°
But
∠A + ∠B + ∠C = 180°
(Sum of interior angles of a triangle = 180°)

⇒ 55° + ∠B + 65° = 180°
⇒ 120° + ∠B = 180°
⇒ ∠B = 180° – 120°
⇒ ∠B = 60°
∵∠C is the greatest angle.
∴ AB is the longest side of the ΔABC. [∵ Side opposite to greater angle is larger] and ∠A is the smallest angle.
∴ BC is the shortest side of the ΔABC. [∵ side opposite to smaller angle is shortest]
Hence, AB is the longest side and BC is the shortest side of the triangle.
Question 11.
In figure, D is a point on the side AC of ΔABC and E is a point such that CD = ED. Prove that AB + BC > AE.
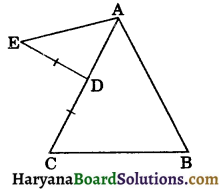
Solution :
In ΔABC, we have
AB + BC > AC, (Sum of any two sides of a triangle is greater than third side)
⇒ AB + BC > CD + AD,
[∵ AC = CD + AD]
⇒ AB + BC > ED + AD ……(i)
[∵ It is given that CD = ED]
In ΔAED, we have
AD + ED > AE ……(ii)
From (i) and (ii), we get
AB + BC > AE. Hence proved
Question 12.
The ABCD is a rectangle in which sides AB and AD produced to E and respectively such that AB = BE and EC = CF. Prove that AD = DF.
Solution :
We have,
AB = BE, (Given)
AB = DC, (Opposite sides of rectangle)
∴ BE = DC ……(i)
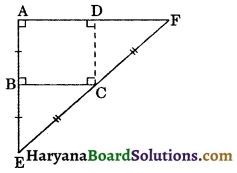
In ΔEBC and ΔCDF, we have
∠EBC = ∠FDC, (Each = 90°)
Hyp. EC = Hyp. CF, (Given)
and BE = DC,
[As proved above in (i)]
∴ ΔEBC ≅ ΔCDF
(By RHS congruence rule)
⇒ BC = DF, (CPCT) … (ii)
But BC = AD …..(iii)
From (ii) and (iii), we get
AD = DF. Hence proved
![]()
Question 13.
In figure, ABCD is a square. P and Q are points on sides AB and CD respectively such that CP = BQ. Prove that :
(i) BP = QC
(ii) ∠BCP = ∠CBQ
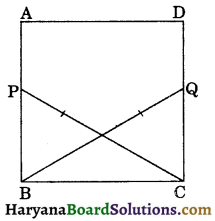
Solution :
In ΔPBC and ΔQCB, we have
∠PBC = ∠QCB,
(Each angle of a square is 90°)
Hyp. PC = Hyp. BQ, (Given)
and BC = BC (Common)
∴ ΔPBC ≅ ΔQCB,
(By RHS congruence rule)
⇒ PB = QC, (CPCT) [Proved (i)]
and ∠BCP = ∠CBQ,(CPCT) [Hence proved (ii)]
Question 14.
In the figure, ABCD is a quadrilateral in which AD = BC. If equal perpendiculars DP and BQ are drawn on diagonal AC. Prove that AP = CQ
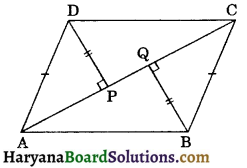
Solution :
In ΔDPA and ΔBQC, we have
∠DPA = ∠BQC,
[∵ DP ⊥ AC and BQ ⊥ AC]
Hyp. AD = Hyp. BC, (Given)
and DP = BQ (Given)
∴ ΔDPA ≅ ΔBQC,
(By RHS congruence rule)
⇒ AP = CQ, (CPCT)
Hence proved
Short Answer Type Questions
Question 1.
In the ΔABC, D is the midpoint of BC, AD is produced upto E so that DE = AD.
Prove that:
(i) ΔABD ≅ ΔECD
(ii) AB = EC
(iii) AB || EC
Solution :
Given: A ΔABC, in which D is the midpoint of BC and AD is produced upto E such that AD = DE.
To prove : (i) ΔΑΒD ≅ ΔECD
(ii) AB = EC
(iii) AB || EC
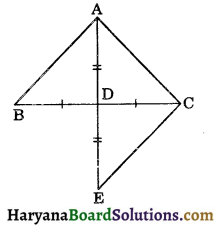
Proof :
(i) In ΔΑΒD and ΔECD, we have
BD = CD
(∵ D is the midpoint of BC)
∠ADB = ∠EDC, (vertically opposite angles)
and AD = DE, (Given)
∴ ΔABD ≅ ΔECD
(by SAS congruence rule) Hence proved
(ii) ΔABD ≅ ΔECD
(As proved above)
⇒ AB = EC, (CPCT) Hence proved
(iii) ΔABD ≅ ΔECD
(As proved above)
⇒ ∠ABD = ∠ECD, (CPCT)
⇒ ∠ABC = ∠ECB,
But these are alternate interior angles.
So, AB || EC, (By theorem 6.3) Hence proved
![]()
Question 2.
In the figure, ABCD is a parallelogram in which E is the mid point of BC. DE is produce and intersect side AB produced at L. Prove that AL = 2CD.
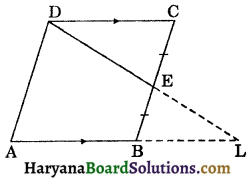
Solution :
Since opposite sides of a parallelogram are equal and parallel.
∴ AB = CD
and AB || CD …………(i)
∵ AB || CD and DL is the transversal.
∴ ∠CDL = ∠ALD
(A pair of alternate interior angles)
⇒ ∠CDL = ∠BLE …………(ii)
Now in ΔCDE and ΔBLE, we have
∠CDE = ∠BLE, [from (ii)]
∠DEC = ∠LEB,
(vertically opposite angles)
and EC = EB,
(E is the midpoint of BC)
∴ ΔCDE ≅ ΔBLE,
(By AAS congruence rule)
⇒ CD = BL (CPCT)
⇒ AB = BL, [Using (i) …(iii)]
Now, AL = AB + BL
⇒ AL = AB + AB, [Using (iii)]
⇒ AL = 2AB
⇒ AL = 2CD, [Using (i)]
Hence proved
Question 3.
In the parallellogram ABCD, the angles A and Care obtuse. Points P and Q are taken on the diagonal BD such that the angles PAD and QCB are right angles. Prove that PA = QC.
Solution :
Given: A parallelogram ABCD such that ∠A and ∠C are obtuse and ∠PAD = ∠QCB = 90°.
To prove: PA = QC.
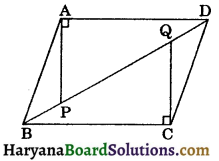
Proof : Since opposite sides of a parallelogram are parallel and equal.
∴ AD = BC and AD || BC …(i)
∵ AD || BC and BD is the transversal
⇒ ∠ADB = ∠CBD, (A pair of alternate interior angles)
⇒ ∠ADP = ∠CBQ …(ii)
Now, in ΔPAD and ΔQCB, we have
∠PAD = ∠QCB, (Each = 90°)
AD = BC [From (i)]
and ∠ADP = ∠CBQ, [From (ii)]
∴ ΔPAD ≅ ΔQCB,
(By ASA congruence rule)
⇒ PA = QC, (CPCT)
Hence proved
Question 4.
In the figure, ABCD is a square in which P, Q and R are the points in AB, BC and CD respectively such that AP = BQ = CR. Prove that:
(i) PB = QC
(ii) PQ = QR
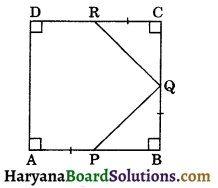
Solution :
∵ ABCD is a square and we know that each side of a square is equal.
∴ AB = BC = CD = DA
Now, AB = BC
⇒ AB – AP = BC – AP
(Subtracting AP from both sides)
⇒ AB – AP = BC – BQ (∵ AP = BQ)
⇒ PB = QC …………..(i) Hence Proved.
(ii) Now in triangles PBQ and QCR, we have
PB = QC [From (i)]
∠PBQ = ∠QCR
[∵ Each angle of a square is 90°]
and BQ = CR (Given)
ΔPBQ ≅ ΔQCR
(By SAS congruence rule)
⇒ PQ = QR (CPCT) Hence Proved.
![]()
Question 5.
In the figure, ΔABC is the right-angled at B. Squares ABPQ and ACDE are draw on the sides AB and AC of ΔABC respectively. Prove that :
(i) ΔQAC ≅ ΔBAE
(ii) QC = BE
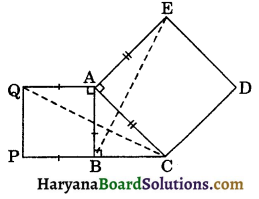
Solution :
(i) We have
∠QAB = ∠CAE
(Each angle of the square is 90°)
⇒ ∠QAB + ∠BAC = ∠CAE + ∠BAC,
(Adding ∠BAC on both sides)
⇒ ∠QAC = ∠BAE ……(i)
Now, in ΔQAC and ΔBAE, we have
AQ = AB, (Equal sides of square ABPQ)
∠QAC = ∠BAE, [From (i)]
and AC = AE, (Equal sides of square ACDE)
∴ ΔQAC ≅ ΔBAE, (By SAS congruence rule)
Hence proved
(ii) ΔQAC ≅ ΔBAE,
(As proved above)
⇒ QC = BE (CPCT)
Hence proved
Question 6.
In figure, the lines segment joining the midpoints P and Q of opposite sides AD and BC of quadrilateral ABCD is perpendicular to both these sides. Prove that the other sides of the quadrilateral are equal. [NCERT Exemplar Problems]

Solution :
Join BP and CP.
In ΔPQB and ΔPQC, we have
BQ = QC,
[∵ Q is the midpoint of BC]
∠PQB = ∠PQC, [Each = 90°]
and PQ = PQ, (Common)
∴ ΔPQB ≅ ΔPQC,
(By SAS congruence rule)
⇒ BP = CP, (CPCT) …(i)
and ∠BPQ = ∠CPQ, (CPCT) …(ii)
Now, ∠APQ = ∠DPQ, (Each = 90°)
⇒ ∠APQ – ∠BPQ = ∠DPQ – ∠BPQ,
(Subtracting ∠BPQ from both sides)
⇒ ∠APQ – ∠BPQ = ∠DPQ – ∠CPQ,
[Using (ii)]
⇒ ∠APB = ∠DPC …(iii)
Now, in ΔAPB and ΔDPV, we have
AP = PD, (∴ Pis the midpoint of AD)
∠APB = ∠DPC, [From …(iii)]
and BP = CP, [From (i)]
∴ ΔAPB ≅ ΔDPC,
(By SAS congruence rule)
⇒ AB = CD, (CPCT)
Or other sides of the quadrilateral are equal. Hence proved
Question 7.
If the diagonals of a quadrilateral bisect each other at right angles and ∠A = 90° prove that ABCD is a square.
Solution :
Given: A quadrilateral ABCD, in which diagonals AC and BD bisect each other at 90° and ∠A = 90°
To prove: ABCD is a square
i.e., AB = BC = CD = DA and
∠A = 90°.
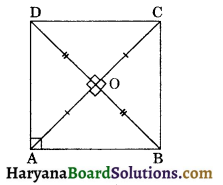
Proof: In ΔAOD and ΔAOB, we have
OD = OB (Given, diagonals bisect each other)
∠AOD = ∠AOB, (Each = 90°)
and AO = AO (Common)
∴ ΔAOD ≅ ΔAOB
(By SAS congruence rule)
⇒ AD = AB (CPCT) …(i)
Similarly we can prove that
ΔAOD ≅ ΔAOB
(By SAS congruence rule)
⇒ AB = BC ……(ii)
(CPCT)
and ΔBOC ≅ ΔDOC
(By SAS congruence rule)
⇒ BC = CD …….(iii) (CPCT)
From (i), (ii) and (iii), we get
AD = AB = BC = CD
and ∠A = 90 (Given)
Hence, ABCD is a square. Proved
![]()
Question 8.
In the figure, ∠ABC = 70° and AB = AC = CD. Find the value of x.
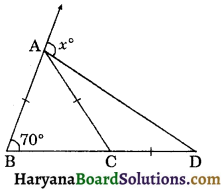
Solution :
In the ΔABC, we have AB = AC, (Given)
⇒ ∠ABC = ∠ACB, [∵ Angles opposite to equal sides are equal]
⇒ 70° = ∠ACB [∵ ∠ABC = 70°]
⇒ ∠ACB = 70°
Now in ΔACD, we have
AC = CD (Given)
⇒ ∠DAC = ∠ADC, ………(i)
[∵ Angles opposite to equal sides are equal]
In ΔACD, we have
∠ACB = ∠DAC + ∠ADC,
[By theorem 6.8]
⇒ 70° = ∠ADC + ∠ADC [From (i)]
⇒ 2∠ADC = 70°
⇒ ∠ADC = \(\frac {70°}{2}\) = 35° ……….(ii)
(Now in ΔABD, we have
x° = ∠ABD + ∠ADB
⇒ x° = ∠ABC + ∠ADC
⇒ x° = 70° + 35°,
[∵∠ABC = 70° and from (ii), ∠ADC = 35°]
⇒ x° = 105°
Hence, x° = 105°
Question 9.
In the figure, ABC is an isosceles triangle with AB = AC. BE and CF are respectively bisectors of ∠B and ∠C. Prove that ΔFCB ≅ ΔEBC.
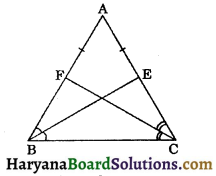
Solution :
In ΔABC, we have AB = AC (Given)
⇒ ∠ABC = ∠ACB ……….(i)
(Angles opposite to equal sides are equal)
⇒ \(\frac {1}{2}\)∠ABC = \(\frac {1}{2}\)∠ACB (Multiply by 1/2 on both sides)
⇒ ∠EBC = ∠FCB ……..(ii)
[∵ BE and CF are the bisectors of ∠B and ∠C respectively]
Now in ΔFCB and ΔEBC,
∠FBC = ∠ECB, [From (i)]
∠FCB = ∠EBC, [From (ii)]
and BC = BC, (Common)
∴ ΔFCB ≅ ΔEBC, (By ASA congruence rule)
![]()
Question 10.
If bisector of the vertical angle of a triangle bisects the base, show that the triangle is isosceles. [NCERT Exemplar Problems]
Solution :
Given: A ΔABC in which AP is the bisector of vertical angle A bisects BC on Pie., BP = CP.
To prove AB = AC.
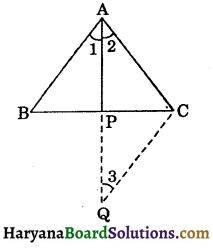
Construction: Produce AP to Q, so that AP = PQ. Join C to Q.
Proof: In ΔABP and ΔQCP, we have
BP = CP, (∵ AP bisects BC)
∠APB = ∠QPC,
(Vertically opposite angles)
and AP = PQ. (By construction)
∴ ΔABP ≅ ΔQCP,
(By SAS congruence rule)
⇒ AB=QC, (CPCT) …(i)
and ∠1 = ∠3, (CPCT) …(ii)
But ∠1 = ∠2, (Given) …(iii)
From (ii) and (iii), we get
∠2 = ∠3
⇒ AC = QC, …(iv)
(Sides opposite to equal angles are equal)
From (i) and (iv), we get
AB = AC
So, ΔABC is an isosceles triangle. Hence proved
Question 11.
In the figure, equilateral triangles APB and AQC are drawn on the sides of a ΔABC. If AB = AC, prove that CP = BQ.
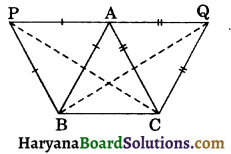
Solution :
Since, ΔAPB and ΔAQC are equilateral triangles.
AB = PB …(i) [Sides of equilateral triangle)
and AC = CQ ………(ii)
AB = AC (Given)…(iii)
From (i), (ii) and (iii), we get
PB = CQ …(iv)
∠ABP = ∠ACQ, ………….(v)
[Each = 60°]
∠ABC = ∠ACB, …(vi)
[∵ AB = AC]
Adding (v) and (vi), we get
∠ABP + ∠ABC = ∠ACQ + ∠ACB
⇒ ∠PBC = ∠QCB …(vii)
Now in ΔPBC and ΔQCB, we have
PB = CQ, [From (iv)]
∠PBC = ∠QCB, (From (vii)]
and BC = BC (Common)
∴ ΔPBC ≅ ΔQCB,
(By SAS congruence rule)
⇒ CP = BQ. (CPCT)
Hence proved
Question 12.
In the figure, CP is the bisector of ∠C meets AB on P. A point Q lies on CP such that AP = AQ. Prove that ∠CAQ = ∠ABC.

Solution :
In ΔAPQ, we have
AP= AQ
∠APQ = ∠AQP ……….(i)
[Angles opposite to equal sides are equal]
∵ CP is the bisector of ∠C.
⇒ ∠ACP = ∠BCP ……….(ii)
In ΔBPC, we have
∠APC = B + ∠BCP,
[By theorem 6.8]
⇒ ∠APQ = ∠B + ∠ACP, ……(iii)
[Using (ii)]
In ΔAQC, we have
∠AQP = ∠CAQ + ∠ACQ
[By theorem 6.8]
⇒ ∠AQP = ∠CAQ + ∠ACP …(iv)
From (i), (iii) and (iv), we get
∠B + ∠ACP = ∠CAQ + ∠ACP
⇒ ∠B = ∠CAQ
⇒ ∠ABC = ∠CAQ. Hence proved
![]()
Question 13.
In a parallelogram ABCD diagonals AC and BD are equal. Find the measure of angle B.
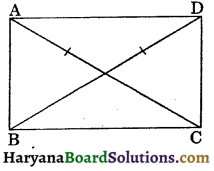
Solution :
We have, ABCD is a parallelogram. AC and BD are its diagonals.
∴ AB = CD, ……(i) (Opposite sides of a parallelogram)
Now in ΔABC and ΔDCB, we have
AB = CD, [From (i)]
AC = BD, (Given)
and BC = BC, (Common)
∴ ΔABC ≅ ΔDCB.
(By SSS congruence rule)
⇒ ∠ABC = ∠DCB, (CPCT) …(ii)
Now AB || CD and transversal BC intersects them at B and C respectively. ∠ABC + ∠DCB = 180°
(Sum of co-interior angles is 180°)
⇒ ∠ABC + ∠ABC = 180°
[From (ii), ∠DCB = ∠ABC]
⇒ 2∠ABC = 180°
⇒ ∠ABC = \(\frac {180°}{2}\) = 90°
Hence measure of ∠B = 90°
Question 14.
In the figure, ΔPQR is a triangle in which PM ⊥ QR. Prove that :
(i) PQ > PM
(ii) PQ + PR > 2PM.
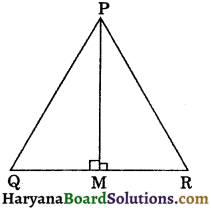
Solution :
(i) In right-angled ΔPQM, we have
Proof : ∠PQM + ∠QPM + ∠PMQ = 180°,
(Sum of interior angles of a triangle = 180°)
⇒ ∠PQM + ∠QPM + 90° = 180°
⇒ ∠PQM + ∠QPM = 180° – 90°
⇒ ∠PQM + ∠QPM = 90°
∴ ∠PQM and ∠QPM are acute angles.
⇒ ∠PMQ > ∠PQM
⇒ PQ > PM ………….(i)
(Side opposite to greater angle is larger)
Hence proved
(ii) Similarly, In right-angled ΔPRM, we have
∠PRM + ∠RPM = 90°
⇒ ∠PRM and ∠RPM are acute angles.
⇒ ∠PMR > ∠PRM
⇒ PR > PM ………….(ii)
(Side opposite to greater angle is larger)
Adding (i) and (ii), we get
PQ + PR > PM + PM
⇒ PQ + PR > 2PM. Hence proved
Question 15.
In the figure, BM and CM are the bisectors of ∠B and ∠C respectively and AC > AB. Prove that CM > BM.
Solution :
In ΔABC, we have
AC > AB (Given)
⇒ ∠B > ∠C [Angle opposite to longer side is greater]
⇒ \(\frac {1}{2}\)∠B > \(\frac {1}{2}\)∠C
(Multiply by 1/2 on both sides)
⇒ ∠MBC > ∠MCB, [∵ BM and CM are bisectors of ∠B and ∠C respectively]
∴ ∠MBC = \(\frac {1}{2}\)∠B and ∠MCB = \(\frac {1}{2}\)∠C)
⇒ CM > BM, (Side opposite to larger angle is longer)
Hence proved
Long Answer Type Questions
Question 1.
In a right-angled triangle, if one of the acute angles is double the other, prove that the hypotenuse is double the shortest side. [NCERT Exemplar Problems]
Solution :
Given: A ΔPQR such that
∠PQR = 90° and ∠R = 2.∠P.
To prove: PR = 2RQ.
Construction: Produce RQ to S such that QS = QR. Join PS.
Proof: ∠R = 2∠P, (Given)
Let ∠P = x, ∠R = 2x
In right-angled ΔPQR, we have
∠P + ∠R + ∠Q = 180°
(∵ Sum of interior angles of a Δ = 180°)
⇒ x + 2x + 90° = 180°
⇒ 3x = 180° – 90°
⇒ 3x = 90°
⇒ x = \(\frac {90°}{3}\) = 30°
∴ ∠P = 30° and ∠R = 2 × 30° = 60°
Now, ΔPQR and ΔPQS, we have
QR = QS, (By construction)
∠PQR = ∠PQS, (Each = 90°)
and PQ = PQ, (Common)
∴ ΔPQR ≅ ΔPQS
(By SAS congruence rule)
⇒ ∠R = ∠S (CPCT)
⇒ ∠R = ∠S = 60°
⇒ ΔPRS is an equilateral triangle.
RS = PS = PR, …(i) (Sides of an equilateral triangle)
But RQ = QS, (By construction)
∴ RS = RQ + QS
⇒ RS = RQ + RQ
⇒ RS = 2RQ
⇒ PR = 2RQ, [Using (i)]
Hence proved
![]()
Question 2.
Prove that the medians of an equilateral triangle are equal.
Solution :
Given: An equilateral ΔABC such that AL, BM and CN are its medians.
To prove: AL = BM = CN.
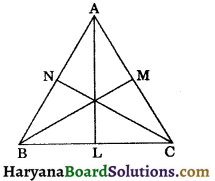
Proof: ΔABC is an equilateral triangle.
∴ AB = BC = AC ……………..(i)
⇒ AB = BC
⇒ \(\frac {1}{2}\)AB = \(\frac {1}{2}\)BC
(Multiply by 1/2 on both sides)
⇒ AN = BL …………….(ii)
(∵ CN and AL are medians)
Now in ΔALB and ΔCNA, we have
AB = AC, [From (i)]
∠ABL = ∠CAN, (Each = 60°)
and BL = AN, [From (ii)]
∴ ΔALB ≅ ΔCNA,
(By SAS congruence rule)
⇒ AL = CN, (CPCT) …(iii)
Similarly, ΔΑLC ≅ ΔΒΜΑ,
(By SAS congruence rule)
⇒ AL = BM (CPCT) …(iv)
From (iii) and (iv), we get
AL = BM = CN
Hence, medians of an equilateral triangle are equal.
Proved
Question 3.
In the figure, BCDE is a square and ΔABC is an equilateral triangle. Prove that :
(i) ∠BAE = 15°
(ii) AE = AD.
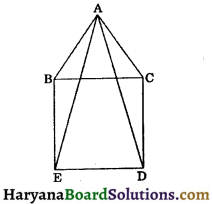
Solution :
∠ABE = ∠ABC + ∠CBE
∠ABE = 60° + 90°,
⇒ ∠ABE = 150° …….(i)
Similarly, ∠ACD = 60° + 90° = 150° …(ii)
In ΔABE and ΔACD, we have
AB = AC, (Sides of an equilateral triangle)
∠ABE = ∠ACD,
[From (i) and (ii)]
and BE = CD, (Square’s sides)
∴ ΔABE ≅ ΔACD,
(By SAS congruence rule)
AE = AD, (CPCT)
Proved (ii)
∵ AB = BC,
(Sides of an equilateral triangle)
and BE = BC, (Square’s sides)
⇒ AB = BE
⇒ ∠BAE = ∠BEA, ………….(iii)
(Angles opposite to equal sides are equal)
Now in ΔABE, we have
∠ABE + ∠BAE + ∠BEA= 180°,
(Sum of interior angles of a triangle = 180°)
⇒ 150° + ∠BAE + ∠BAE = 180°,
[From (iii), ∠BEA = ∠BAE]
⇒ 2∠BAE = 180° – 150°
⇒ ∠BAE = \(\frac {30°}{2}\)
⇒ ∠BAE = 15°. Proved (i).
Question 4.
In ΔPQR, ∠Q = 2∠R, PM is the bisector of ∠QPR meets QR on M and PQ = MR (see figure). Find the ∠PQR.
Solution :
In ΔPQR, we have
∠Q = 2∠R (Given)
Let ∠Q = 2∠R = 2x
⇒ ∠R = x
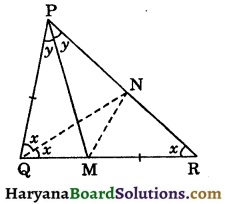
PM is the bisector of ∠QPR (given).
Let ∠QPM = ∠RPM = y
Draw QN, bisector of ∠PQR.
∴ ∠PQN = ∠RQN = x
In ΔNQR, ∠NQR = ∠QRN = x
⇒ QN = NR …(i) (∵ Sides opposite to equal angles are equal)
In ΔPQN and ΔMRN, we have
PQ = MR. (Given)
∠PQN = ∠MRN = x
and QN = RN, [From (i)]
∴ ΔPQN ≅ ΔMRN,
(By SAS congruence rule)
⇒ ∠QPN = ∠RMN, (CPCT)
⇒ ∠QPN = ∠RMN = 2y …(ii) (CPCT)
and PN = MN, (CPCT)
⇒ ∠NMP = ∠MPN = y, …………(iii)
(Angles opposite to equal sides are equal)
In ΔPQM, we have
∠PMR = ∠PQM + ∠QPM,
(By theorem 6.8)
⇒ ∠PMR = 2x + y ……(iv)
But ∠PMR = ∠NMP + ∠RMN,
⇒ ∠PMR = y + 2y
[Using (ii) and (iii)]
⇒ ∠PMR = 3y ……(v)
From (iv) and (v), we get
2x + y = 3y
⇒ 2x = 2y
⇒ x = y
In ΔPQR, we have
∠P + ∠Q + ∠R = 180°
⇒ 2y + 2x + x = 180°
⇒ 2x + 2x + x = 180°, (∵ y = x)
⇒ 5x = 180°
⇒ x = \(\frac {180°}{5}\) = 36°
∴ ∠PQR = 2 × 36° = 72°
Hence, ∠PQR = 72°
![]()
Question 5.
In the figure, ABCD is a square. X, Y and Z are the points in AB, BC and CD respectively, such that AX = BY = CZ.
Prove that :
(i) XY = YZ
(ii) ∠XYZ = 90°.
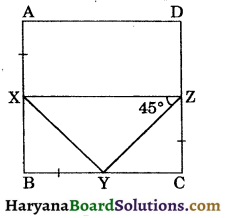
Solution :
(i) ∵ ABCD is a square.
∴ AB = BC = CD = DA
Now AB = BC …(i)
and AX = BY (Given)…(ii)
AB – AX = BC – BY
[Subtracting (ii) from (i)]
⇒ BX = CY …….(iii)
(∵ AX = BY)
and BY = CZ (Given) …….(iv)
Now in ΔXBY and ΔYCZ, we have
BX = YC, [From (iii)]
∠XBY = ∠YCZ [Each = 90°]
and BY = CZ, [From (iv)]
∴ ΔXBY = ΔYCZ
(By SAS congruence rule)
⇒ XY = YZ (CPCT)
Hence proved
(ii) ∵ XY = YZ, (As proved above)
⇒ ∠YXZ = ∠YZX [Angles opposite to equal sides one equal]
∴ ∠YXZ = ∠YZX = 45°
In ΔXYZ, we have
∠YXZ + ∠YZX + ∠XYZ = 180°
⇒ 45° + 45° + ∠XYZ = 180°
⇒ 90° + ∠XYZ = 180°
⇒ ∠XYZ = 180° – 90°
⇒ ∠XYZ = 90°. Hence proved
Question 6.
In the figure, ABC is an isosceles triangle in which AB = AC, AE ⊥ BC and F is the mid point of BE and D is the mid
point of EC. Prove that :
(i) E is the midpoint of BC.
(ii) AF = AD,
(iii) ΔABF ≅ ΔACD.

Solution :
(i) In ΔAEB and ΔAEC, we have
∠AEB = ∠AEC, (Each = 90°)
Hyp. AB = Hyp. AC, (Given)
and AE = AE (Common)
∴ ΔAEB ≅ ΔAEC,
(By RHS congruence rule)
⇒ BE = EC, (CPCT) …(i)
Or E is the midpoint of BC. Hence Proved
(ii) BE = EC, (As proved above)
⇒ \(\frac {1}{2}\)BE = \(\frac {1}{2}\)EC
(Multiply by 1/2 on both sides)
⇒ FE = ED,
[∵ F is the midpoint of BE and D is the midpoint of EC
∴ FE = \(\frac {1}{2}\)BE and ED = \(\frac {1}{2}\)EC]
Now in ΔAFE and ΔADE, we have
FE = ED, (As proved above)
∠AEF = ∠AED, (Each = 90°)
and AE = AE (Common)
∴ ΔAFE = ΔADE,
(By SAS congruence rule)
⇒ AF = AD, (CPCT) …(ii)
Hence proved
(iii) In ΔABF and ΔACD, we have
AB = AC, (Given)
BF = CD.
[∵ BE = EC ⇒ \(\frac {1}{2}\)BE = \(\frac {1}{2}\)EC
F and D are midpoints of BE and EC respectively ∴ BF = CD]
and AF = AD, [From (ii)]
∴ ΔABF ≅ ΔACD, (By SSS congruence rule)
Hence proved
Question 7.
Show at the difference of any two sides of a triangle is less than the third side.
Solution :
Given: A ΔABC.
To prove :
(i) AC – AB < BC.
(ii) BC – AC < AB.
(iii) BC – AB < AC.
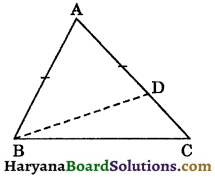
Construction: Take a point D on AC such that AD = AB. Join BD.
Proof: In ΔABD, side AD has been produced to C.
∠BDC > ∠ABD ………..(i)
(∵ Exterior angle of a triangle is greater than each of interior opposite angle)
In ΔBCD, side CD has been produced to A.
∠ADB > ∠DBC ………..(ii)
[∵ Exterior angle of a triangle is greater than each of interior opposite angle]
In ΔABD, we have
AB = AD, (By construction)
⇒ ∠ABD = ∠ADB ………..(iii)
(Angles opposite to equal sides are equal)
From (ii) and (iii), we get
∠ABD > ∠DBC
From (i) and (iv), we get
∠BDC > ∠DBC
⇒ BC > CD, (Side opposite to greater angle is larger)
⇒ CD < BC
⇒ AC – AD < BC
⇒ AC – AB < BC (By construction)
Similarly, BC – AC < AB and BC – AB < AC.
Hence proved
![]()
Question 8.
In the figure, ABCD is a square and P, Q and R are points on the sides AB, BC and CD respectively such that AP = BQ = CR. Prove that ∠PQR = 90°.
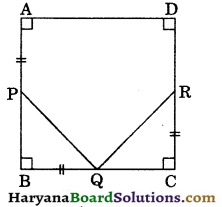
Solution :
In square ABCD, we have
AP = BQ = CR(Given) …(i)
AB = BC, (Square’s sides)
⇒ AB – AP = BC – AP
(Subtracting AP from both sides)
⇒ AB – AP = BC – BQ,
[From (i), AP = BQ]
⇒ PB = QC ………(ii)
Join PR.
Now, in ΔPBQ and ΔQCR, we have
PB = QC,
[As proved above in (ii)]
∠PBQ = ∠QCR,
(Each angle of square = 90°)
and BQ = CR (Given)
∴ ΔPBQ ≅ ΔQCR
(By SAS congruence rule)
⇒ ∠2 = ∠5, (CPCT) … (iii)
and ∠6 = ∠1 (CPCT)
AB || CD
⇒ PB || CR and PR is the transversal.
⇒ ∠BPR + ∠CRP = 180°,
(Sum of allied angles = 180°)
⇒ ∠2 + ∠3 + ∠1 + ∠4 = 180° …… (iv)
and ∠5 + ∠PQR + ∠6 = 180°, …… (v)
(Linear pair)
From (iv) and (v), we get
∠2 + ∠3 + ∠1 + ∠4 = ∠5 + ∠PQR + ∠6
⇒ ∠2 + ∠3 + ∠1 + ∠4 = ∠2 + ∠PQR + ∠1
[From (iii), ∠5 = ∠2 and ∠6 = ∠1]
⇒ ∠3 + ∠4 = ∠PQR …(vi)
In ΔPQR, we have
∠3 + ∠4 + ∠PQR = 180° (Sum of interior angles of a triangle = 180°)
⇒∠PQR + ∠PQR = 180° [Using (vi)]
⇒ 2∠PQR = 180°
⇒ ∠PQR = \(\frac {180°}{2}\) = 90°
Hence, ∠PQR = 90°. Hence Proved
Question 9.
ABCD is a square in which P and Q are points on the sides BC and CD respectively such that PQ || BD. If AR bisects the PQ.
prove that :
(i) ∠PAR = ∠QAR
(ii) If AR produce it will passes through C.
Solution :
(i) In ΔBCD, we have
BC = DC, (Square’s sides)
⇒ ∠CBD = ∠CDB
(Angles opposite to equal sides are equal)
Now, PQ || BD (Given) …(i)
∠CPQ = ∠CBD …….(ii)
(Corresponding angles)
∠CQP = ∠CDB, …….(iii)
(Corresponding angles)
From (i), (ii) and (iii), we get
∠CPQ = ∠CQP
⇒ CP = CQ
(Side opposite to equal angles are equal)

Now BC = CD
⇒ BC – CP = CD – CP
⇒ BC – CP = CD – CQ, [∵ CP = CQ]
⇒ BP = DQ ……….(iii)
In ΔABP and ΔADQ, we have
AB = AD, (Square’s sides)
∠ABP = ∠ADQ, (Each = 90°)
and BP = DQ [Using (iii)]
∴ ΔABP ≅ ΔADQ,
[By SAS congruence rule]
⇒ AP = AQ, (CPCT) …(iv)
Now, in ΔAPR and ΔAQR, we have
AP = AQ, [As proved in (iv)]
AR = AR (Common)
and PR = QR [It is given that R is the midpoint of PQ]
∴ ΔAPR ≅ ΔΑQR,
(By SSS congruence rule)
⇒ ∠PAR = ∠QAR, (CPCT)
Proved
(ii) If AR produce and join to C. It must be a straight line we have PQ || BD.
∠BSR + ∠PRS = 180°,
(Sum of allied angles = 180°)
⇒ ∠PRC + ∠PRS = 180°, [∵ ∠BSR and ∠PRC are corresponding angles ∴ ∠PRC = ∠BSR]
∴ Point A, R and C lies on the line AC.
⇒ AC is a straight line.
Hence, if AR is produced it will passes through C.
Proved
![]()
Question 10.
Squares ABCD and AFPQ are drawn on the sides AD and AF of parallelogram ADEF. Prove that BQ = AE.
Solution :
We have
AQ = AF …………(i)
(Square’s sides)
DE = AF …………(ii)
(Opposite sides of a parallelogram)
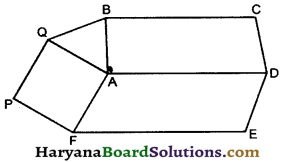
From (i) And (ii), we get
AQ = DE …………(iii)
⇒ ∠BAQ + 90° + ∠FAD + 90° = 360° (from fig.)
⇒ ∠BAQ + ∠FAD = 360°- 90° – 90°
⇒ ∠BAQ + ∠FAD = 180°
⇒ ∠BAQ = 180° – ∠FAD …(iv)
AF || DE, (Opposite sides of a parallelogram)
⇒ ∠ADE + ∠FAD = 180°,
(Sum of allied angles = 180°)
⇒ ∠ADE = 180° – ∠FAD …(v)
From (iv) and (v), we get
∠BAQ = ∠ADE …..(vi)
Now in ΔBAQ and ΔADE, we have
BA = AD, (Square’s sides)
∠BAQ = ∠ADE, [As proved in (vi)]
and AQ = DE, [As proved in (iii)]
∴ ΔBAQ ≅ ΔADE,
(By SSS congruence rule)
⇒ BQ = AE, (CPCT)
Hence proved.
Question 11.
In the figure, ABC is a triangle in which PQ ⊥ BC and PR ⊥ AB. If BP and CP are the bisectors of ∠B and ∠C respectively. Prove that :
(i) PR = PT,
(ii) AP bisects ∠A.

Solution :
(i) In ΔPRB and ΔPQB, we have
∠PRB = ∠PQB, (Each = 90°)
∠RBP = ∠QBP, [BP is the bisector of ∠B]
and BP = BP, (Common)
∴ ΔPRB ≅ ΔPQB,
(By AAS congruence rule)
⇒ PR = PQ, (CPCT) …(i)
Now draw PT ⊥ AC and join AP.
Again in ΔPQC and ΔPTC, we have
∠PQC = ∠PTC (Each = 90°)
∠PCQ = ∠PCT, (PC is the bisector of ∠C)
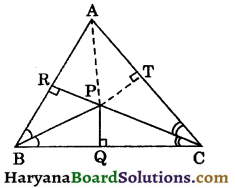
and PC = PC (Common)
∴ ΔPQC ≅ ΔPTC,
(By AAS congruence rule)
⇒ PQ = PT, (CPCT)
⇒ PT = PQ …………(ii)
From (i) and (ii), we get
PR = PT ……..(iii)
Hence Proved
(ii) Now in ΔARP and ΔATP, we have
∠ARP = ∠ATP, (Each = 90°)
Hyp. AP = Hyp. AP (Common)
and PR = PT,
[As proved above in (iii)]
∴ ΔARP ≅ ΔATP,
(By RHS congruence rule)
⇒ ∠RAP = ∠TAP (CPCT)
⇒ AP bisects the ∠A.
Hence proved
![]()
Question 12.
E is the point on the side AC of ΔABC such that AB = AE. If AD bisects ∠A, prove that :
(i) BD = DE,
(ii) ∠ABE > ∠C.
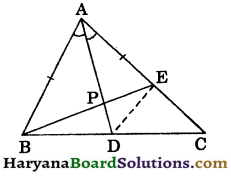
Solution :
(i) In ΔABE, we have
AB = AE (Given)
⇒ ∠ABE = ∠AEB,
(Angles opposite to equal sides are equal)
⇒ ∠ABP = ∠AEP
In ΔABP and ΔAEP, we have
∠PAB = ∠PAE (Given)
∠ABP = ∠AEP,
[As proved above in (i)]
and AP = AP, (common)
∴ ΔABP ≅ ΔAEP,
(By AAS congruence rule)
⇒ BP = PE (CPCT) …….(ii)
and ∠APB = ∠APE (CPCT)
⇒ ∠EPD = ∠BPD, ………..(iii)
(∵ ∠APB = ∠EPD and ∠APE = ∠BPD)
Now in ΔBPD and ΔEPD, we have
BP = PE, [As proved above in (ii)]
∠BPD = ∠EPD,
[As proved above in (iii)]
and PD = PD, (common)
∴ ΔBPD ≅ ΔΕPD,
(By SAS congruence rule)
⇒ BD = DE (CPCT)
Hence proved
(ii) In ΔBEC, we have
∠AEB = ∠C + ∠EBC, (By theorem 6.8)
∴ ∠AEB > ∠C
⇒ ∠ABE > ∠C, [∵ ∠AEB = ∠ABE]
Hence proved
Question 13.
In the figure, AD, BE and CF are medians of ΔABC. Prove that :
2(AD + BE + CF) > AB + BC + CA.
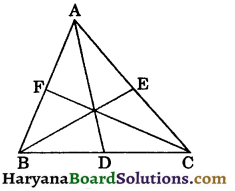
Solution :
In ΔABD, we have
BD + AD > AB, [∵ Sum of any two sides of a triangle is greater than third side]
⇒ \(\frac {1}{2}\)BC + AD > AB ……..(i)
Again in ΔACD, we have
CD + AD > AC,
[∵ Sum of any two sides of a Δ is greater than third side]
⇒ \(\frac {1}{2}\)BC + AD > AC …………(ii)
Adding (i) and (ii), we get
\(\frac {1}{2}\)BC + AD + \(\frac {1}{2}\)BC + AD > AB + AC
⇒ 2AD + BC > AB + AC …………….(iii)
Similarly, we can prove that
2BE + AC > AB + BC ………(iv)
and 2CF + AB > AC + BC ……………(v)
Adding (iii), (iv) and (v), we get
2AD + 2BE + 2CF + AB + BC + AC > AB + AC + AB + BC + AC + BC
⇒ 2AD + 2BE + 2CF > AB + BC + AC
2(AD + BE + CF) > AB + BC + CA.
Hence proved
Question 14.
In the figure, ABC is an equilateral triangle in which BP and CP are bisectors of ∠B and ∠C respectively. If PQ || AB and PR || AC, prove that BQ = QR = RC.
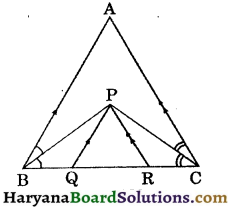
Solution :
We have ΔABC is an equilateral triangle.
∠A = ∠B = ∠C = 60°
∠PBQ = \(\frac {1}{2}\)∠B = \(\frac {60°}{2}\) = 30°……(i) [∵ BP is the bisector of ∠B]
and ∠PCR = \(\frac {1}{2}\)∠C = \(\frac {60°}{2}\) = 30°…(ii)
[∵ CP is the bisector of ∠C]
∵ PQ || AB
⇒ ∠PQR = ∠ABQ,
[Corresponding angles]
⇒ ∠PQR = 60° ……….(iii)
[∵ ∠ABQ = ∠ABC = 60°]
and PR || AC
⇒ ∠PRQ = ∠ACR
[Corresponding angles]
⇒ ∠PRQ = 60° ……(iv) [∵ ∠ABR = ∠ACB60°C]
In ΔPQR, we have
∠PQR + ∠PRQ + ∠QPR = 180°, (Sum of interior angles of a triangle = 180°)
⇒ 60° + 60° + ∠QPR = 180°,
[Using (iii) and (iv)]
⇒ ∠QPR = 180° – 60° – 60°
⇒ ∠QPR = 60°
∴ ΔPQR is an equilateral triangle.
⇒ PQ = QR = RP ……..(v)
In ΔPBQ, we have
∠PQR = ∠PBQ + ∠BPQ,
⇒ 60° = 30° + ∠BPQ,
[Using (i) and (iii)]
⇒ ∠BPQ = 60° – 30° = 30°
⇒ ∠PBQ = ∠BPQ, (Each = 30°)
⇒ PQ = BQ …(vi)
Similarly, PR = RC …(vii)
From (v), (vi) and (vii), we get
BQ = QR = RC.
Hence proved
Multiple Choice Questions
Choose the correct option in each of the following:
Question 1.
Which of the following is not a rule ‘for congruence of triangles’ :
(NCERT Exemplar Problems)
(a) SSS
(b) RHS
(c) SSA
(d) SAS
Solution :
(c) SSA
![]()
Question 2.
If ΔABC ≅ ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true :
[NCERT Exemplar Problems]
(a) BC = PQ
(b) AC = PR
(c) QR = BC
(d) AB = PQ
Solution :
(a) BC = PQ
Question 3.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if : [NCERT Exemplar Problems]
(a) BC = EF
(b) AC = DE
(c) AC = EF
(d) BC = DE
Solution :
(b) AC = DE
Question 4.
Two equilateral triangles are congruent, when :
(a) their sides are proportional
(b) their sides are equal
(c) their angles are equal
(d) None of these
Solution :
(b) their sides are equal
Question 5.
ΔABC ≅ ΔPQR, if BC = 4 cm, ∠B = 60° and ∠C = 70°, then which of the following is true :
(a) QR = 4 cm, ∠P = 60°
(b) PQ = 4 cm, ∠Q = 60°
(c) QR = 4 cm, ∠R = 60°
(d) QR = 4 cm, ∠Q = 60°
Solution :
(d) QR = 4 cm, ∠Q = 60°
Question 6.
In figure, ΔABD ≅ ΔACD, AB = AC, BD = CD. Name the criteria by which the triangles are congruent :
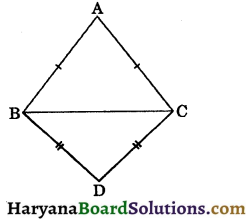
(a) SSS
(b) SAS
(c) ASA
(d) RHS
Solution :
(a) SSS
![]()
Question 7.
In the figure, ΔABD ≅ ΔACD. Name the criteria by which the triangles are congruent :
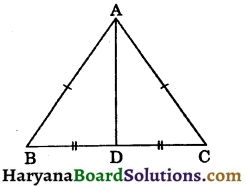
(a) SSS
(b) ASA
(c) AAS
(d) RHS
Solution :
(a) SSS
Question 8.
Two right-angled triangles ADB and ADC are congruent if AB = AC. Name the criteria by which the triangles are congruent :
(a) RHS
(b) SAS
(c) ASA
(d) SSA
Solution :
(a) RHS
Question 9.
In the figure, if AB = PQ, BC = QR and AC = PR, then which of the following is true :
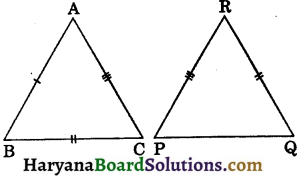
(a) ΔABC ≅ ΔRPQ
(b) ΔACB ≅ ΔRQP
(c) ΔABC ≅ ΔPQR
(d) ΔABC ≅ ΔPRQ
Solution :
(a) ΔABC ≅ ΔRPQ
Question 10.
In ΔPQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is : [NCERT Exemplar Problems]
(a) 4 cm
(b) 5 cm
(c) 2 cm
(d) 2.5 cm
Solution :
(a) 4 cm
![]()
Question 11.
In ΔABC, BC = AB and ∠B = 80°. Then ∠A is equal to [NCERT Exemplar Problems]
(a) 80°
(b) 40°
(c) 50°
(d) 100
Solution :
(c) 50°
Question 12.
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are:
[NCERT Exemplar Problems]
(a) isosceles but not congruent
(b) isosceles and congruent
(c) congruent but not isosceles
(d) neither congruent nor isosceles
Solution :
(a) isosceles but not congruent
Question 13.
In the figure, PQ = PR and QS = RS, then ratio of ∠PQS : ∠PRS is :
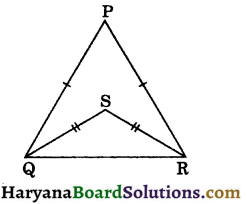
(a) 1 : 2
(b) 2 : 1
(c) 2 : 3
(d) 1 : 1
Solution :
(d) 1 : 1
Question 14.
In a ΔABC, we have:
(a) AB + BC > AC
(b) AB + AC = BC
(c) AB + BC < AC
(d) None of these
Solution :
(a) AB + BC > AC
![]()
Question 15.
In ΔABC, we have :
(a) AB + BC < AC
(b) AC – AB < BC (c) BC – AC > AB
(d) BC – AB > AC
Solution :
(b) AC – AB < BC