HBSE 8th Class Maths Solutions Chapter 7 घन और घनमूल Ex 7.2

Haryana State Board HBSE 8th Class Maths Solutions Chapter 7 घन और घनमूल Ex 7.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 7 घन और घनमूल Ex 7.2

प्रश्न 1.
अभाज्य गुणनखंडन विधि द्वारा निम्नलिखित में से प्रत्येक संख्या का घनमूल ज्ञात कीजिए
(i) 64
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
हल:
(i) 64 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) = 2² × 2²
\(\sqrt[3]{64}\) = 2 × 2 = 4

(ii) 512 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) = (2)³ × (2)³ × (2)³
\(\sqrt[3]{512}\) = 2 × 2 × 2 = 8

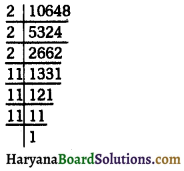
(iii) 10648 = \(\underline{2 \times 2 \times 2}\) × \(\underline{11 \times 11 \times 11}\)
= (2)³ × (11)³
= (2 × 11)³
= 22³
\(\sqrt[3]{10648}\) = 22

(iv) 27000 = \(\underline{3 \times 3 \times 3}\) × \(\underline{10 \times 10 \times 10}\)
= (3)³ × (10)³
= (3 × 10)³
= 30³
\(\sqrt[3]{27000}\) = 30

(v) 15625 = \(\underline{5 \times 5 \times 5}\) × \(\underline{5 \times 5 \times 5}\)
= (5)³ × (5)³
= (5 × 5)³
= 25³
\(\sqrt[3]{15625}\) = 25

(vi) 13824 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\)
= (2)³ × (2)³ × (2)³ × (3)³
= (2 × 2 × 2 × 3)³
= 24³
\(\sqrt[3]{15625}\) = 24

(vii) 110592 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\)
= (2)³ × (2)³ × (2)³ × (2)³ × (3)³
= (2 × 2 × 2 × 2 × 3)³
= 48³
\(\sqrt[3]{15625}\) = 48

(viii) 46656 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\) × \(\underline{3 \times 3 \times 3}\)
= (2)³ × (2)³ × (3)³ × (3)³
= (2 × 2 × 3 × 3)³
= 36³
\(\sqrt[3]{15625}\) = 36

(ix) 46656 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{7 \times 7 \times 7}\)
= (2)³ × (2)³ × (2)³ × (7)³
= (2 × 2 × 2 × 7)³
= 56³
\(\sqrt[3]{15625}\) = 56

(x) 91125 = \(\underline{5 \times 5 \times 5}\) × \(\underline{3 \times 3 \times 3}\) × \(\underline{3 \times 3 \times 3}\)
= (5)³ × (3)³ × (3)³
= (5 × 3 × 3)³
= 45³
\(\sqrt[3]{15625}\) = 45

प्रश्न 2.
बताइये सत्य है या असत्य-
(i) किसी भी विषम संख्या का घन सम होता है ।
(ii) एक पूर्ण घन दो शून्यों पर समाप्त नहीं होता है ।
(iii) यदि किसी संख्या का वर्ग 5 पर समाप्त होता है, तो उसका घन 25 पर समाप्त होता है ।
(iv) ऐसा कोई पूर्ण घन नहीं है, जो 8 पर समाप्त होता है ।
(v) दो अंकों की संख्या का घन तीन अंकों वाली संख्या हो सकती है।
(vi) दो अंकों की संख्या के घन में सात या अधिक अंक हो सकते हैं ।
(vii) एक अंक वाली संख्या का घन एक अंक वाली संख्या हो सकती है।
हल:
(i) असत्य
(ii) सत्य
(iii) असत्य
(iv) असत्य
(v) असत्य
(vi) असत्य
(vii) सत्य ।

प्रश्न 3.
आपको यह बताया जाता है कि 1331 एक पूर्ण घन है। क्या बिना गुणनखण्ड किये आप यह अनुमान लगा सकते हैं कि इसका घनमूल क्या है। इसी प्रकार 4913, 12167 और 32768 के घनमूलों के अनुमान लगाइए।
हल :
दिया है – 1331
1331 के सबसे दाईं ओर के अंक से प्रारम्भ करते हुए तीन-तीन अंकों के समूह बनाएँ । यह समूह 1 और 331 हैं । इस स्थिति में एक समूह 331 है, जिसमें तीन अंक हैं और दूसरा समूह 1 है, जिसमें 1 अंक है। सबसे पहले हम 331 लेते हैं। इसकी इकाई का अंक 1 है-
अत: घनमूल की इकाई का अंक 1 लेंगे ।
अब 1 को देखते हैं।
अत: घनमूल की दहाई का अंक 1 लेंगे ।
इस प्रकार,
\(\sqrt[3]{1331}\) = 11
हाँ, हम बिना गुणनखण्ड करके अनुमान लगा सकते हैं कि यह पूर्ण घन है।

(i) 4913 – 4913 के सबसे दाईं ओर के अंक से प्रारम्भ करते हुए तीन-तीन अंकों के समूह बनाएंगे । ये समूह 4 तथा 913 हैं । इस स्थिति में एक समूह 913 है जिसमें तीन अंक हैं और दूसरा समूह 4 है, जिसमें 1 अंक है।
पहले हम 913 लेंगे । इसकी इकाई का अंक 3 है । तो घनमूल की इकाई का अंक 7 लेते हैं, दूसरे समूह 4 को लेंगे।
1 का घन 1 है और 2 का घन 8 है । संख्या 4, संख्याओं 1 तथा 8 के बीच में स्थित है। अब 1 और 2 में से छोटी संख्या 1 है । 1 में इकाई का अंक स्वयं 1 है । हम 1 को वाँछित घनमूल का दहाई के अंक लेते हैं।
इस प्रकार, \(\sqrt[3]{4913}\) = 17

(ii) 12167 – 12167 के दाई ओर के अंक से प्रारम्भ करते हुए तीन-तीन अंकों के दो समूह 12 तथा 167 बनायेंगे । इनमें एक में 2 अंक तथा दूसरे में 3 अंक हैं ।
पहले हम 167 को लेंगे, इसकी इकाई का अंक 7 है तो घनमूल की इकाई का अंक 3 लेंगे ।
दूसरे समूह 12 को लेंगे । 2 का घन 8 है और 3 का घन 27 है । अत: संख्या 12, संख्याओं 8 और 27 के बीच में
अब, 2 और 3 में छोटी संख्या 2 है।
2 में इकाई का अंक स्वयं 2 है ।
हम 2 को वांछित घनमूल के दहाई का अंक लेते हैं।
इस प्रकार, \(\sqrt[3]{12167}\) = 23

(iii) 32768 – 32768. के दाई ओर के अंक प्रारम्भ करते हुए तीन-तीन अंकों के दो समूह 32 तथा 768 बनते पहले हम 768 को लेते हैं । इसकी इकाई का अंक 8 है। हम वांछित घनमूल की इकाई का अंक 2 लेते हैं।
दूसरे समूह 32 को लेते हैं । 3 का घन 27 है और 4 का घन 64 है। संख्या 32, संख्याओं 27 तथा 64 के बीच में स्थित है।
अब, 3 और 4 में छोटी संख्या 3 है।।
3 में इकाई का अंक स्वयं 3 है । हम 3 को वांछित घनमूल के दहाई का अंक लेते हैं।
इस प्रकार, \(\sqrt[3]{32768}\) = 32.