Haryana State Board HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Ex 5.5 Textbook Exercise Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Exercise 5.5
प्रश्न 1.
निम्नलिखित में से कौन लम्ब रेखाओं के उदाहरण हैं?
(a) मेज के ऊपरी सिरे की आसन्न भुजाएँ
(b) रेल पथ की पटरियाँ
(c) अक्षर L बनाने वाले रेखाखण्ड
(d) अक्षर V बनाने वाले रेखाखण्ड।
हल :
(a) हाँ, लम्ब,
(b) नहीं,
(c) हाँ, लम्ब,
(d) नहीं।
![]()
प्रश्न 2.
मान लीजिए रेखाखण्ड PQ रेखाखण्ड XY पर लम्ब है। मान लीजिए ये परस्पर बिन्द A पर प्रतिच्छेद करते हैं। ∠PAY की माप क्या है ?
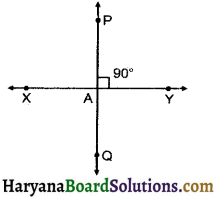
हल :
∠PAY की माप = 90°, [क्योंकि PO ⊥ XY]
प्रश्न 3.
आपके ज्यामिति बक्स में दो सेट स्क्वेयर हैं। इनके कोनों पर बने कोणों के माप क्या हैं ? क्या इनमें कोई ऐसी माप है जो दोनों में उभयनिष्ठ है ?
हल :
एक 30°, 60°, 90° सेट स्क्वे यर और दूसरा 45°, 45°, 90° सेट स्क्वे यर है।
स्पष्टतः उभयनिष्ठ कोण = 90°.
![]()
प्रश्न 4.
इस आकृति को ध्यान से देखिए। रेखा l, रेखा m पर लम्ब है।
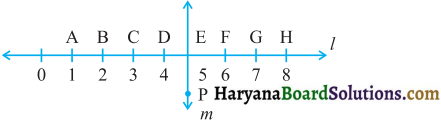
(क) क्या CE = EG है ?
(ख) क्या रेखा PE रेखाखण्ड CG को समद्विभाजित करती है ?
(ग) कोई दो रेखाखण्डों के नाम लिखिए जिनके लिए PE लम्ब समद्विभाजक है।
(घ) क्या निम्नलिखित सत्य हैं ?
(i) AC > FG
(ii) CD = GH
(iii) BC < EH
हल :
(क) ∵ CE = CD + DE
= 1 + 1 = 2 इकाई
और EG = EF + FG
= 1 + 1 = 2 इकाई
∴ CE = EG.
(ख) ∵ CE = EG
अतः E, CG का मध्य-बिन्दु है।
∴ PE, CG का समद्विभाजक है।
(ग) ∵ DE = EF [क्योंकि प्रत्येक 1 इकाई है]
अत: PE, DF का लम्ब समद्विभाजक है।
पुनः CE = EG = 2 इकाई
अत: PE, CG का लम्ब समद्विभाजक है।
(घ) (i) ∵ AC = AB + BC
= 1 + 1 = 2 इकाई
और FG = 1 इकाई
∴ AC > FG सत्य है।
(ii) ∵ CD = 1 इकाई
GH = 1 इकाई
CD = GH, सत्य है।
(iii) ∵ BC = 1 इकाई
और EH = EF + FG + GH
= 1 + 1 + 1 = 3 इकाई
BC < ED, सत्य है।