HBSE 12th Class Practical Work in Geography Solutions Chapter 2 आंकड़ों का प्रक्रमण

Haryana State Board HBSE 12th Class Geography Solutions Practical Work in Chapter 2 आंकड़ों का प्रक्रमण Textbook Exercise Questions and Answers.

Haryana Board 12th Class Practical Work in Geography Solutions Chapter 2 आंकड़ों का प्रक्रमण

बहुविकल्पीय प्रश्न

प्रश्न 1.
निम्नांकित चार विकल्पों में से सही विकल्प चुनिए –
(i) केंद्रीय प्रवृत्ति का जो माप चरम मूल्यों से प्रभावित नहीं होता है वह है ?
(क) माध्य
(ख) माध्य तथा बहुलक
(ग) बहुलक
(घ) माध्यिका
उत्तर:
(क) माध्य।

(ii) केंद्रीय प्रवृत्ति का वह माप जो किसी वितरण के उभरे भाग से हमेशा संपाती होगा वह है –
(क) माध्यिका
(ग) माध्य
(ख) माध्य तथा बहुलक
(घ) बहुलक।
उत्तर:’
(ख) माध्य तथा बहुलक।

(iii) ऋणात्मक सहसंबंध वाले प्रकीर्ण अंकन में अंकित मानी के वितरण की दिशा होगी –
(क) ऊपर बाएँ से नीचे दाएँ
(ख) नीचे बाएँ से ऊपर दाएँ
(ग) बाएँ से दाएँ
(घ) ऊपर दाएँ से नीचे बाएँ।
उत्तर:
(क) ऊपर बाएँ से नीचे दाएँ।

प्रश्न 2.
निम्नलिखित प्रश्नों के उत्तर लगभग 30 शब्दों में दीजिए-
(i) माध्य को परिभाषित कीजिए ।
उत्तर:
माध्य इसे औसत मान भी कहा जाता है। यह एक औसत कई मात्राओं के योग का निरूपक होता है। यह एक ऐसी संख्या होती है जो न्यूनाधिक रूप में संख्याओं की श्रृंखला को निरूपित या प्रदर्शित करती हैं। अतः औसत को कुल जनसंख्या के एक मध्यवर्ती मान या प्रवृत्ति के रूप में लिया जा सकता है इसका मूल्य अधिकतम तथा न्यूनतम मूल्य के बीच होता है।

(ii) बहुलक के उपयोग के क्या लाभ हैं? उत्तर – बहुलक के उपयोग के लाभ इस प्रकार हैं –
1. बहुलक की गणना सरलता से निरीक्षण विधि द्वारा की जा सकती है।
2. बहुलक पर श्रृंखला के चरम मूल्यों का प्रभाव नहीं पड़ता।
3. किसी श्रृंखला में सबसे अधिक बार आने के कारण, यह उसका सर्वोत्तम प्रतिनिधि होता है।
4. अंकों के प्रभाव की हालत में भी बहुलक ज्ञात किया जा सकता
5. बहुलक की व्यावहारिक उपयोगिता अधिक है किसी वस्तु की अधिक मात्रा के कारण उसका उत्पादन अधिक होता है।
6. बहुलक को रेखाचित्र द्वारा भी प्रदर्शित करके इसे सरल रूप दिया जा सकता है।

(iii) अपकिरण किसे कहते हैं?
उत्तर:
अपकिरण केंद्रीय प्रवृत्तियों के अंकों के बिखराव के मापन से संबंधित है अपरिकण किसी हदों के मापन के लिए भी प्रयोग किया जा सकता है जो किसी व्यक्तिगत विषय तथा संख्यात्मक आंकड़ों की प्रवृत्ति के बदलाव अथवा औसत मूल्य के फैलाव से संबंधित है। इसलिए हम कह सकते हैं कि अपकिरण एक डिग्री है। जो फैलाव या प्रकीर्ण अथवा केंद्रीय मानक मापन के फेरबदल से संबंधित है।

(iv) सहसंबंध किसे कहते हैं?
उत्तर:
सहसंबंध (Correlation ) –
दो भिन्न प्रकार के चरों के एक बंटन को दविचरीय वितरण कहते हैं, ये दोनों चर उस अवस्था में आपस में सह-संबंधित कहलाते हैं जब एक चर में परिवर्तन दूसरे चर में संगती परिवर्तन उत्पन्न होता है। प्रथम चर जिसके कारण दूसरे चर में परिवर्तन होता है स्वतंत्र (x) कहलाता है जबकि दूसरा चर आश्रित चर (v) के रूप में जाना जाता है। दो चरों के मध्य साहचर्य की मात्रा तथा दिशा का आंकलन सरल अथवा द्विचर सह संबंध कहलाता है सह संबंध की माप का सर्वाधिक प्रचलित स्वरूप पियर्सन का गुणन आघूर्ण सह संबंध गुणांक (r) है। का मूल्य +1 से 1 के बीच प्रसारित होता है।

(v) पूर्ण सहसंबंध किसे कहते हैं?
उत्तर:
पूर्ण सहसंबंध दो चरों के मध्य विशिष्ट साहचार्य को दर्शाने के लिए प्रयोग होता है यह दो मानों के बिखराव अथवा प्रकीर्णन दर्शाते हैं। इसे प्रकीर्ण आरेख अथवा प्रकीर्ण अंकन भी कहते हैं जब एक सरल रेखा प्रकीर्ण आरेख के निचले बाएँ से ऊपरी दाएँ भाग की ओर जाती है तो वह पूर्ण धनात्मक सहसंबंध कहलाता है। सहसंबंध को अधिकतम सीमाएँ 1 (एक) होती है। यह 1 से ज्यादा कभी भी नहीं हो सकती। सहसंबंध 1 को पूर्ण सहसंबंध कहते हैं।

(vi) सहसंबंध की अधिकतम सीमाएँ क्या हैं?
उत्तर:
सहसंबंध की अधिकतम सीमाएँ (एक) होती है। यह 1 से ज्यादा कभी भी नहीं हो सकती।

प्रश्न 3.
निम्नलिखित प्रश्नों के उत्तर लगभग 125 शब्दों में दीजिए –
(i) आरेखों की सहायता से सामान्य तथा विषम वितरणों में माध्य, माध्यिका तथा बहुलक की सापेक्षिक स्थितियों की व्याख्या कीजिए।
उत्तर:
केन्द्रीय प्रवृत्ति के तीनों मापों की तुलना सामान्य वितरण वक्र की सहायता से आसानी से की जा सकती है। यह इस प्रकार है –

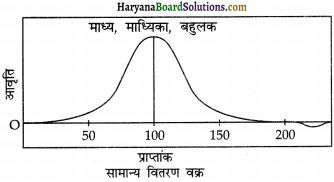
सामान्य वितरण की एक विशेषता होती है। इसमें माध्य, माध्यिका तथा बहुलक का मान समान होता है क्योंकि वितरण सामान्य सममित होता है। ज्यादातर इकाइयाँ वितरण के माध्य में अथवा माध्य के निकट होती है। ज्यादा उच्च तथा ज्यादा निम्न मूल्यों की बारंबारता अधिक नहीं होता तथा विरले ही होते हैं। अगर आंकड़े किसी प्रकार विषम और विकृत हो तो माध्य, माध्यिका और बहुलक संपाती नहीं होंगे और विषम आंकड़ों के प्रभाव पर विचार करने की जरूरत है।

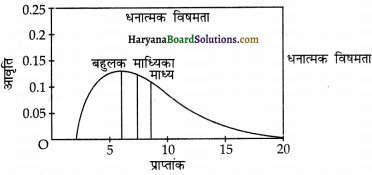
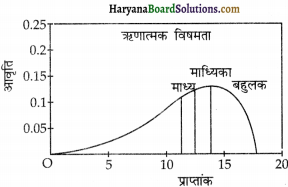
(ii) माध्य, माध्यिका तथा बहुलक की उपयोगिता पर टिप्पणी कीजिए।
उत्तर:
माध्य, माध्यिका तथा बहुलक काफी उपयोगी हैं इनकी विशेषता इस प्रकार है-

माध्य –
1. सरलता – समांतर माध्य सभी केंद्रीय प्रवृत्तियों में से उत्तम है जिसे समझना सरल है।
2. प्रतिनिधि मूल्य- माध्य सभी मूल्यों का प्रतिनिधि मूल्य है।
3. निश्चित मूल्य – समांतर माध्य सदा एक ही रहता है जिसका निश्चित मूल्य होता है।
4. स्थिर मूल्य- माध्यम का स्थिर मूल्य होता है। किसी श्रेणी के निर्देशन में परिवर्तन से प्रभाव नहीं पड़ता। यह संतुलित मूल्य है।

माध्यिका –
1. माध्यिका ज्ञात करना एक सरल विधि है।
2. माध्यिका चरम मूल्यों से प्रभावित नहीं होती है।
3. अपूर्ण आँकड़ों के बावजूद इसकी गणना की जा सकती है।4. खुले सिरे वाली श्रृंखला में माध्यिका का मूल्य सुगमता से प्राप्त हो जाता है।
5. माध्यिका का मूल्य ग्राफ की सहायता से भी ज्ञात किया जा सकता है।
6. माध्यिका का मूल्य सदैव निश्चित होता है।

बहुलक –
1. बहुलक की गणना सरलता से निरीक्षण विधि द्वारा की जा सकती है।
2. बहुलक पर श्रृंखला के चरम मूल्यों का प्रभाव नहीं पड़ता।
3. किसी शृंखला में सबसे अधिक बार आने के कारण, यह उसका सर्वोत्तम प्रतिनिधि होता है।
4. अंकों के अभाव की हालत में भी बहुलक ज्ञात किया जा सकता है।
5. बहुलक की व्यावहारिक उपयोगिता अधिक है। किसी वस्तु की अधिक मात्रा के कारण उसका उत्पादन अधिक होता है।

(iii) एक काल्पनिक उदाहरण की सहायता से मानक विचलन के गणना की प्रक्रिया समझाइए।
उत्तर:
विचलन के माप की दूसरी विधि, जो औसत माध्य का प्रयोग कर प्राप्त की जाती है मानक विचलन कहलाती है। इसे वर्ग माध्य-मूल विचलन भी कहते हैं। मानक विचलन किसी श्रेणी के | विभिन्न मूल्यों के समांतर माध्य से निकाले गए विचलनों के वर्गों के माध्य का वर्गमूल होता है। इसे ग्रीक भाषा के अक्षर (σ) सिगमा से प्रकट किया जाता है।

(σ) सिगमा
मानक विचलन की गणना की प्रक्रिया। निम्नलिखित उदाहरण की सहायता से मानक विचलन की गणना की जाती है –
(सिगमा) σ = \(\sqrt{\frac{\sum(x-\bar{x})^2}{N}}\) यहाँ σ = मानक विचलक (S.D)
\(\sum(x-\bar{x})^2\) = Sum total of squares of Deviation
N = Numbers of items.
उपरोक्त विधि अधिक उबाऊ बन जाती है अगर x की कीमत दशमलव पाइंट में तथा प्रेक्षणों की संख्या बहुत बड़ी हो। इस हालात में हम निम्नलिखित shortcut method का प्रयोग कर सकते हैं-
\(\sqrt{\frac{\sum x^2}{N}-\left(\frac{\sum \bar{x}}{N}\right)^2}\)

उदाहरण:
निम्नलिखित तालिका हमें वर्षा के पिछले दस सालों के आंकड़े पेश करता है। मानक विचलक की गणना –

(iv) प्रकीर्णक का कौन-सा माप सबसे अधिक अस्थिर है तथा क्यों ?
उत्तर:
यह देखा जाता है कि माध्य दो आंकड़ों के समूहों से प्राप्त किया जाता है। जैसे कि इन तालिकाओं में दिखाया गया है –

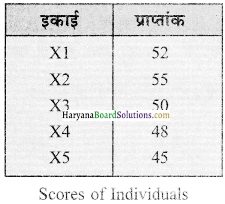
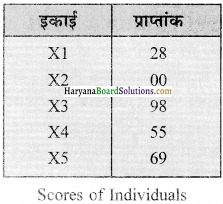
इन तालिकाओं में माध्य एकसमान है जो 50 है। तालिका में उच्चतम व निम्नतम मान क्रमशः 55 तथा 45 हैं। तालिका में दिए गए वितरण में ये अधिकतम तथा न्यूनतम मान क्रमश: 98 तथा 00 हैं। यहां पर दोनों ही वितरणों का माध्य एकसमान है। तथा द्वितीय वितरण जो कि अधिक अस्थिर तथा विषम है कि अपेक्षा प्रथम वितरण स्थिर और समरूप हैं। इससे हमें वितरण या श्रेणी के संघटन की प्रकृति का ज्ञान होता है तथा इसकी सहायता से दिए हुए वितरण की तुलना स्थिरता अथवा समरूपता के आधार पर हो जाती है।

(v) सहसंबंध की गहनता पर एक विस्तृत टिप्पणी लिखिए।
उत्तर:
जब सहसंबंध की दिशा ऋणात्मक तथा धनात्मक के विषय में संदर्भ आ जाता है तो स्वाभाविक तौर पर यह जानने के लिए जिज्ञासा जागृत होती है कि दोनों चरों में अनुरूपता तथा साहचर्य की गहनता की मात्रा कितनी है। इस साहचर्य की गहनता की मात्रा गणितीय दृष्टि से अधिकतम 1 (एक) तक होती हैं। इस मात्रा में सहसंबंध की दिशा का पहलू जोड़ने पर इसका अधिकतम विस्तार – 1 से शून्य की ओर होते हुए +1 तक होता है। इसका मान किसी भी स्थिति में एक से ज्यादा नहीं हो सकता।

(vi) कोटि सहसंबंध की गणना से विभिन्न चरण कौन-से हैं ?
उत्तर:
निम्नलिखित चरणों के द्वारा कोटि सहसंबंध की गणना की जा सकती है –
(1) आंकड़े के अनुकरण से संबंधित X-Y परिवर्ती या जो कि अभ्यास में दी गयी है अथवा उनकी पहले तथा दूसरे कॉलम में रखकर तालिका बना ली।
(2) दोनों परिवर्तीयों की अलग-अलग दर्जों में दो-दो । X – दर्जी की परिवर्ती को तीसरे चरण में रिकार्ड कर XR (Rank dx ) शीर्षक दिया जाए। इसी प्रकार रैंक Y- परिवर्ती (YR) को चौथे चरण में रखा जाए।
(3) अब दोनों XR अथवा YR को प्राप्त करने के बाद दोनों ही सैटों के रैंक का रिकार्ड करके पांचवें चरण में रखा जाए।
(4) इस प्रकार के हर मतभेद के चौकोर और अन्य कॉलमों को प्राप्त किया जाए और इनके मान को छठवें कॉलम में लिखा जाए।
(5) इसके बाद रैंक सहसंबंध की संगणना की जाए, निम्नलिखित समता का प्रयोग करके –
\(\mathrm{P}=1-\frac{6 \sum \mathrm{D}^2}{\mathrm{~N}\left(\mathrm{~N}^2-1\right)}\) यहाँ पर P = Rank Correlation
ED₂ = Sura of the squares of the difference between two sets of Ranks
N = The number of pairs of X-Y.

अतिरिक्त प्रश्न (Other Questions)

प्रश्न 1.
केंद्रीय प्रवृत्तियों के माप से क्या अभिप्राय है ?
उत्तर:
केंद्रीय प्रवृत्तियों के माप – ‘केंद्रीय प्रवृत्ति के माप’ सांख्यिकी विश्लेषण की एक महत्त्वपूर्ण तकनीक है। कई बार संपूर्ण आँकड़ों के लिए एक प्रतिनिधि मान को प्राप्त करना आवश्यक हो जाता है। यह मान विभिन्न आँकड़ों के बीच तुलना करने में सहायक होते हैं। यह माप सभी आँकड़ों के मध्य या केंद्र में होता है, इसलिए इसे केंद्रीय प्रवृत्ति के माप कहते हैं। ऐसे सारांश मान जो विभिन्न बंटन – निरूपकों को दर्शाते हैं, उनको केंद्रीय प्रवृत्ति के मापक कहते हैं। (The summary values that are representative of the various distributions are known as measures of central tendency.) इन मापों में प्रमुख निम्नलिखित माप हैं –
(i) माध्य अथवा औसत (Average or Mean)
(2) माध्यिका (Median)
(3) बहुलक (Mode)

प्रश्न 2.
माध्य किसे कहते हैं ? इसके प्रकार बताओ।
उत्तर:
माध्य (Mean ):
इसे औसत मान भी कहा जाता है। माध्य या औसत कई मात्राओं के योग का निरूपक होता है। यह एक ऐसी संख्या होती है जो न्यूनाधिक रूप में संख्याओं की श्रृंखला को निरूपित या प्रदर्शित करती है। अतः औसत को कुल जनसंख्या के एक मध्यवर्ती मान या प्रवृत्ति के रूप में लिया जा सकता है। इसका मूल्य अधिकतम तथा न्यूनतम मूल्य के बीच होता है।

माध्य तीन प्रकार के होते हैं –
(1) अंकगणितीय माध्य
(2) ज्यामितीय माध्य
(3) हरात्मक (हारमोनिक) माध्य।

प्रश्न 3.
अंकगणितीय माध्य (Arithmetic Mean) से क्या अभिप्राय है ? यह किस प्रकार ज्ञात किया जाता है ?
उत्तर;
अंकगणितीय माध्य (Arithmetic Mean ):
केंद्रीय प्रवृत्ति के माप का सबसे सरल रूप माध्य है, सभी भिन्न-भिन्न मानों के योग की कुल संख्या से भाग देने पर माध्य ज्ञात होता है।

उदाहरण – किसी गांव के पांच विभिन्न परिवारों की मासिक आय ₹100, ₹80, ₹120, ₹90 और ₹60 हैं तो इन परिवारों की माध्य आय =
(1) यह एक सरल विधि है।
(2) श्रेणी के सभी मदों को जोड़ कर ज्ञात करें।
(3) सभी मदों की गिनती ज्ञात करें।
\(\bar{X}=\frac{100+80+120+90+60}{5}=\frac{450}{5}=₹ 90\)
माध्य = \(\overline{\mathrm{X}}=\frac{\sum x}{n}\)

1. अवर्गीकृत आँकड़ों के लिए (For Ungrouped Data) –
किसी भी क्षेत्र में कृषक परिवारों की संख्या तथा X₁, X₂, X₃,………… X_n क्रमश: पहले, दूसरे, तीसरे और वें किसान परिवार की आय को प्रकट करें तो माध्य
\(\overline{\mathrm{X}}=\frac{\mathrm{X}_1+\mathrm{X}_2+\mathrm{X}_3 \ldots \ldots \ldots \mathrm{X}_n}{n}\) = \(\frac{\Sigma X}{n}\)
(जबकि \(\overline{\mathrm{x}}\) = माध्य ∑X = प्रेक्षणों का योग n = संख्या)

2. वर्गीकृत आँकड़ों के लिए (For Grouped Data):
इस अवस्था में माध्य निकालने की दो विधियां हैं –
(1) प्रत्यक्ष विधि (Direct Method)
(2) लघु विधि (Short-cut Method)

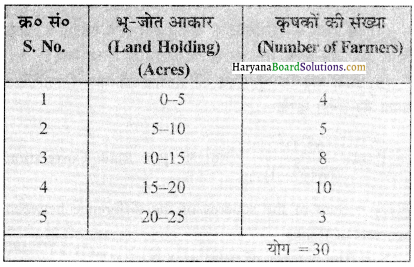
प्रश्न 4.
निम्नलिखित तालिका में दिए गए आँकड़ों के आधार पर माध्य निकालो-

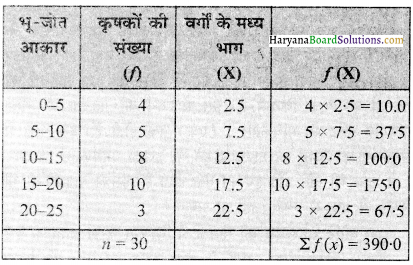
उत्तर:
1. प्रत्यक्ष विधि (Direct Method):
(1) यह एक सरल विधि है। इसमें मदों के साथ आवृत्ति (x) भी दी जाती है।
(2) प्रत्येक मद का मध्यमान (x) ज्ञात करो। इसे आवृत्ति (f) से गुणा करके f (x) ज्ञात करो।
(3) सभी मदों के f (x) का योग ज्ञात करो तथा इसे मदों की संख्या से भाग दें।
\(\overline{\mathrm{X}}=\frac{\sum f(x)}{n}\)
माध्य = \(\overline{\mathrm{X}}=\frac{\Sigma f x}{n}=\frac{390}{30}\) = 13 acres.

2. लघु विधि (Short-cut Method):
(1) प्रत्येक मद (वर्ग) का माध्य मूल्य (x) ज्ञात करो।
(2) एक मद को कल्पित माध्य (अस्थायी माध्य) मान लो (A)
(3) प्रत्येक माध्य मूल्य (x) से कल्पित मूल्य (A) घटा कर विचलन (dx) ज्ञात करो ।
(4) प्रत्येक मद की आवृत्ति (f) को विचलन से गुणा करो तथा इनका योग ∑f (dx) ज्ञात करें।
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d \overline{\mathrm{X}}}{n}\)

अस्थायी माध्य A =12.5 acres

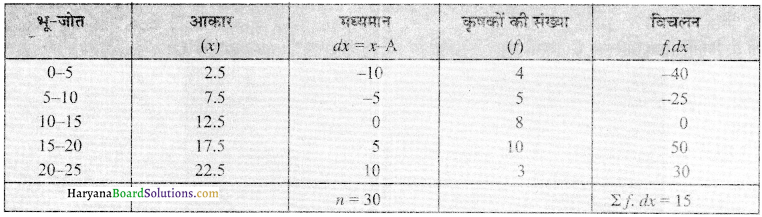
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x}{n}\) = 12.5 + \(\frac {15}{30}\) = 13acres

प्रश्न 5.
निम्नलिखित तालिका में दिए गए आँकड़ों का माध्य निकालो।

उत्तर:
1. प्रत्यक्ष विधि (Direct Method):

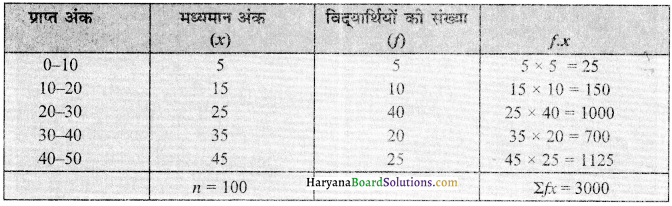
\(\overline{\mathrm{X}}=\frac{\Sigma f x}{n}=\frac{3000}{100}\) = 30 Marks

2. लघु विधि (Short-cut Method) –

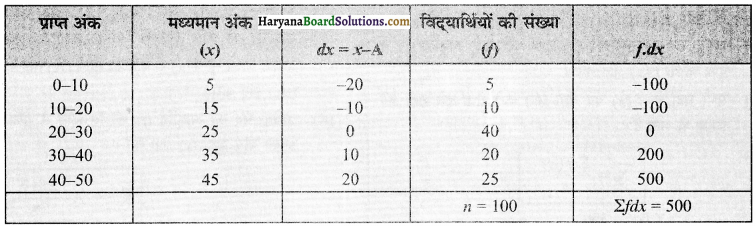
माध्य = \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\sum f d x}{n}\) = 25 + \(\frac {500}{100}\) = 30 marks.

प्रश्न 6.
निम्नलिखित तालिका में किसी स्थान की वर्षा के आँकड़े दिए गए हैं। माध्य ज्ञात करो ।

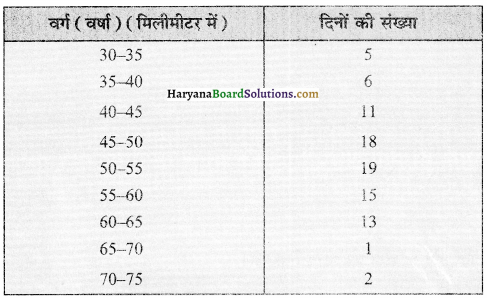
उत्तर:
1. प्रत्यक्ष विधि (Direct Method)

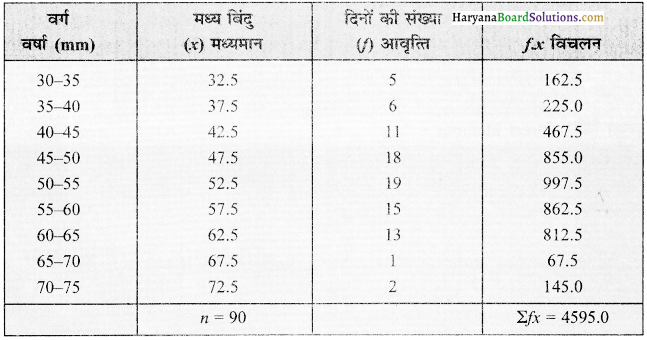
माध्य = \(\overline{\mathrm{X}}=\frac{\Sigma f \cdot x}{n}=\frac{4595}{90}\) = 51.06m.m

2. अप्रत्यक्ष विधि (Indirect method):
अस्थायी (कल्पित) माध्य = A = 50

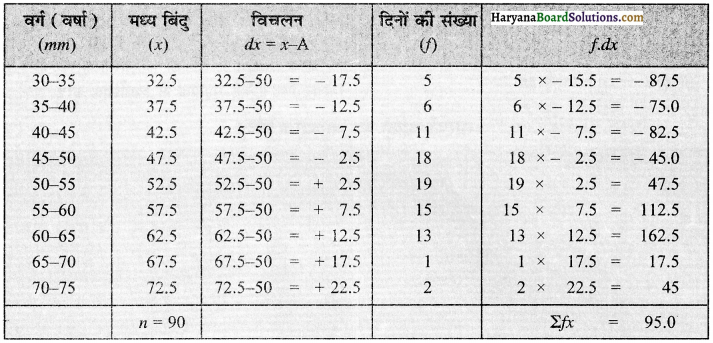
माध्य = \(\overline{\mathrm{X}}=\frac{\Sigma f \cdot x}{n}=\frac{4595}{90}\)
= 50 + \(\frac {95}{90}\)
= 50 + 1.06 = 51.06 m. m

प्रश्न 7.
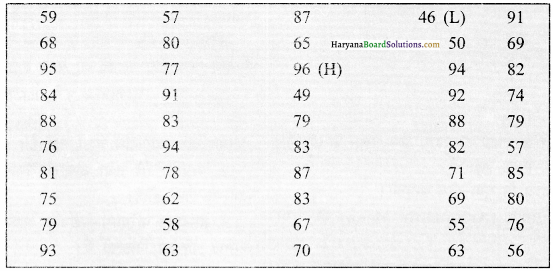
50 छात्रों द्वारा प्राप्त अंकों का प्रतिशत निम्नलिखित है। माध्य ज्ञात करो।

उत्तर:
अंकगणितीय माध्यम की गणना निम्न चरणों में की जाएगी –
चरण (Step):
1. न्यूनतम मान (L) और अधिकतम मान (H) की प्राप्ति।
(यहां L = 46 तथा H = 96)

चरण (Step) 2.
परिसर की गणना करने के लिए अधिकतम से न्यूनतम को घटाएं।
परिसर R = अधिकतम न्यूनतम (R =H – L) = 96 – 46 = 50

चरण (Step) 3.
परिसर को इच्छित संख्या के वर्गों (N) से विभाजित कर वर्ग अंतराल (C. I.) निर्धारित करें।
वर्ग अंतराल C. I. = \(\frac {परिसर}{वर्ग N}\)
5 वर्ग (N) लेने पर अंतराल = \(\frac {50}{5}\) = 10
वर्गों की यह संख्या न तो बहुत अधिक होनी चाहिए और नही बहुत कम।

चरण (Step) 4.
वर्ग सीमा का निर्धारण करें। (निचली तथा ऊपरी सीमा) इसके लिए वर्ग अंतराल को न्यूनतम मान (L) के साथ उतनी बार जोड़ें जब तक कि अधिकतम मान (H) प्राप्त न हो जाए।
इस प्रकार न्यूनतम सीमा अगली सीमा अगली सीमा
इस प्रकार न्यूनतम सीमा = 46 (निम्नतम मान L )
अगली सीमा = 46 + (10 × 1 ) = 56
अगली सीमा = 46 + (10 × 2) = 66
अगली सीमा = 46 + (10 × 3 ) = 76
अगली सीमा = 46 + (10 × 4 ) = 86
और अधिकतम सीमा = 46 + (10 × 5 ) = 96 (अधिकतम मान H )
अतः
प्रथम I वर्ग होगा – 46 से 56
II वर्ग होगा – 56 से 66
III वर्ग होगा – 66 से 76
IV वर्ग होगा – 76 से 86
वर्ग होगा – 86 से 96

चरण (Step) 5.
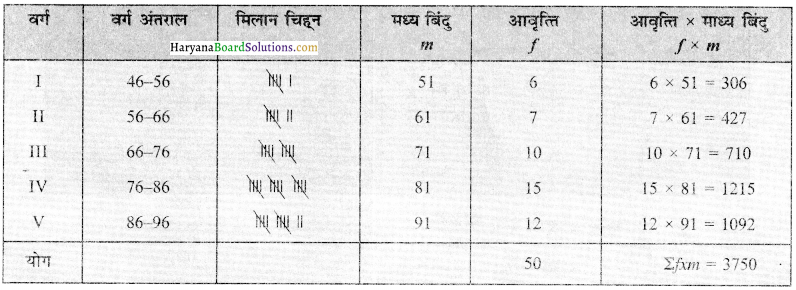
आँकड़ों को बारंबारता सारणी में 5 वर्गों सहित मिलान चिह्नों की सहायता से व्यवस्थित करें।
सारणी-अंकों का बारंबारता बंटन

चरण (Step) 6.
अब बारंबारता को उनके संगत मानों से गुणा करें, उन्हें जोड़कर प्राप्त करते हैं। ∑fxm

चरण (Step) 7.
अंकगणितीय माध्य की गणना सूत्र का प्रयोग करें,
\(\overline{\mathrm{X}}=\frac{\Sigma f x m}{\Sigma f}\) = \(\frac{3750}{50}\) = 75
नोट – बारंबारता की संकल्पना का प्रयोग अन्य प्रकार के औसतों/ माध्यों की गणना से भी किया जाता है।

प्रश्न 8.
समांतर माध्य के गुण-दोष बताओ।
उत्तर:
समांतर माध्य (Arithmatic Mean) के गुण (Merits) –
1. सरल (Simple)-समांतर माध्य सभी केंद्रीय प्रवृत्तियों में से सरल है जिसे समझना बहुत सरल है।
2. प्रतिनिधि मूल्य (Representative Value )-माध्य सभी मूल्यों का प्रतिनिधि मूल्य है।
3. निश्चित मूल्य (Certain Value )-समांतर माध्य सदा एक ही रहता है जिसका निश्चित मूल्य होता है।
4. स्थिर मूल्य (Stable Value )-माध्यम का स्थिर मूल्य होता है। किसी श्रेणी के निर्देशन ( Sample) में परिवर्तन से प्रभाव नहीं पड़ता। यह संतुलित मूल्य है।
5. समूह की तुलना (Comparison )-माध्य की सहायता से अंकों के समूहों की तुलना करना आसान है।
n = 90 ∑f.dx = 95

दोष (Demerits) –
1. चरम मूल्यों का माध्य पर प्रभाव (Effect of Extreme Values)-बहुत बड़ी या बहुत छोटी संख्या माध्य पर प्रभाव डालती है।
उदाहरण:
एक कम्पनी के मैनेजर का मासिक वेतन ₹50,000 है तथा अन्य तीन क्लर्कों का वेतन ₹3,500, 1,500, 1,000 है।
औसत वेतन = \(\frac{50,000+3,500+1,500+1,000}{4}\) = ₹14,000 यह वेतन प्रतिनिधि मूल्य नहीं है।
2. अप्रतिनिधि तथा अवास्तविक – समांतर माध्य श्रेणी में उपस्थित नहीं होता।
3. हास्यप्रद परिणाम – समांतर माध्य से कई बार हास्यप्रद तथा असंगत परिणाम निकलते हैं।
4. भ्रमात्मक निष्कर्ष कई बार समांतर माध्य की सहायता से प्राप्त निष्कर्ष भ्रमात्मक होते हैं।

प्रश्न 9.
गुणोत्तर माध्य किसे कहते हैं ? उदाहरण देकर स्पष्ट करो।
उत्तर:
गुणोत्तर माध्य (Geometric Mean):
n मानों का गुणोत्तर माध्य उदाहरणतः x₁,x₂,x₃,x₄, ……………. x_n मानों के भागफल के वें वर्गमूल के रूप में परिभाषित किया जाता है। अतः इसे गणितीय रूप में निम्नलिखित प्रकार से व्यक्त किया जा सकता है –
गुणोत्तर माध्य = \(\left(x_1, x_2, x_3, x_4, \ldots \ldots \ldots x_n\right)^{\frac{1}{n}}\)
= \(\left(x_1 x_2 x_3 \ldots \ldots \ldots x_n\right)^{\frac{1}{n}}\) निम्नलिखित उदाहरण की सहायता से गुणोत्तर माध्य की गणना की जा सकती है।
उदाहरण:
अर्थव्यवस्था में चार वर्षों की वृद्धि दर को क्रमशः 4, 8, 8 तथा 16 प्रतिशत दिया गया है।
अतः गुणोत्तर माध्य = \((4 \times 8 \times 8 \times 16)^{\frac{1}{4}}\)
यहां n = 4 है क्योंकि मदों की संख्या 4 है।
= 4 × 8 × 8 × 16 = 4096
= 4096 का चतुर्थ मूल 8 प्रतिशत।

गुणोत्तर माध्य के उपयोग-गुणोत्तर माध्य अधिक उपयोगी औसत होता है अगर आँकड़े अनुपात के रूप में हों। अगर आँकड़े परिवर्तन के रूप में हो तो असंगत परिणाम प्राप्त हो सकते हैं।

प्रश्न 10.
माध्यिका किसे कहते हैं ? इसे किस प्रकार ज्ञात किया जाता है ?
उत्तर:
माध्यिका (Median ) – यह केंद्रीय प्रवृत्ति का एक मुख्य माप है। इसका अर्थ है-मध्य मूल। किसी भी श्रेणी की माध्यिका वह मूल्य है जो श्रेणी को दो बराबर भागों में बांटता है। एक भाग में वे मूल्य होते हैं, जो माध्यिका से अधिक होते हैं तथा दूसरे भाग में वे मूल्य होते हैं, जो माध्यिका से कम होते हैं। उदाहरण के लिए 40, 42, 38, 45, 50, 52, 55 की माध्यिका 45 है। माध्यिका किसी दी हुई श्रृंखला के मानों का औसत होता है। इस पर श्रृंखला की चरम सीमाओं का प्रभाव नहीं पड़ता है।

माध्यिका ज्ञात करना –
अवर्गीकृत आँकड़ों के लिए (For Ungrouped Data):
(1) माध्यिका प्राप्त करने के लिए हम पहले आँकड़ों को आरोही तथा अवरोही क्रम में रखते हैं।
(2) इस प्रकार श्रृंखला के मध्य में जो मूल्य आता है, वहा माध्य कहलाता है।
(3) जब आँकड़ों की संख्या विषय ( odd ) हो तो माध्यिका ज्ञात करने का सूत्र –
M = \(\text { Size of }\left(\frac{N+1}{2}\right) \text { th item }\)
M = माध्यिका
N = मदों की संख्या

(4) जब आँकड़ों की संख्या सम (Even) हो तो माध्यिका ज्ञात करने का सूत्र
M = \(\frac{1}{2}\left(\frac{\mathrm{N}}{2} \text { th Item }+\frac{\mathrm{N}}{2}+1 \text { th item }\right)\)
मान लो किसी श्रेणी में 8 संख्याएं हैं तो \(\frac {N}{2}\) संख्या 4th संख्या होगी तथा \(\frac {N}{2}\) + 1 संख्या 5th संख्या होगी। इस प्रकार चौथी तथा पाँचवीं संख्या का औसत ही माध्यिका होगी।

माध्यिका वह मान है जो श्रृंखला को दो बराबर भागों में इस प्रकार बाँटता है कि माध्यिका के चरों के सही-सही केंद्रीय स्थान या स्थिति वाले मान के रूप में लगभग आधे मान इससे नीचे या कम और शेष आधे इसके ऊपर या अधिक होते हैं।
उदाहरण:
पाँच व्यक्तियों, अ ब स द य जिनकी आयु क्रमश: 20, 21, 19, 23 तथा 22 वर्ष दी गई है, के लिए माध्यिका की गणना कीजिए, माध्यिका की गणना निम्नलिखित चरणों में होगी –

चरण 1.
आँकड़ों को एक आरोही या अवरोही क्रम में सारणीबद्ध कीजिए।

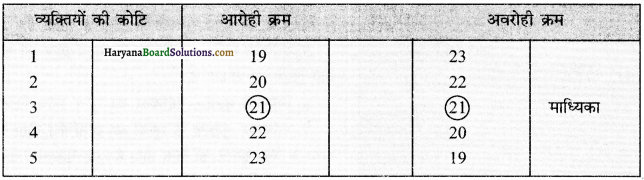
चरण 2.
मध्यवर्ती संख्या का मान ही माध्यिका है।

प्रश्न 11.
किसी बस्ती के 12 परिवारों की मासिक आय नीचे दी गई है, इसकी माध्यिका ज्ञात करो –
परिवारों की आय (₹ में)
140, 150, 130, 135, 170, 190, 500, 210, 205, 195, 290, 200
उत्तर:
आँकड़ों को आरोही क्रम में लिखने पर –
130, 135, 140, 150, 170, 190, 195, 200, 205, 210, 290, 500

आँकड़ों को अवरोही क्रम में लिखो
500, 290, 210, 205, 200, 195, 190, 170, 150, 140, 135, 130

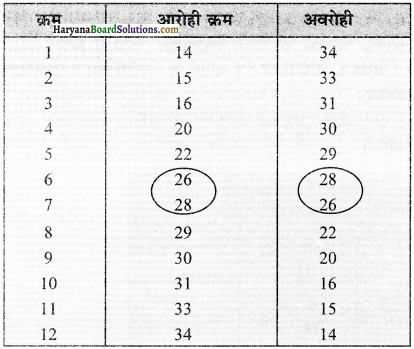
माध्यिका (M) =

प्रश्न 12.
निम्नलिखित सारणी में दिल्ली के मासिक तापमान के आँकड़े दिए गए हैं। दिल्ली के तापमान की माध्यिका ज्ञात करें।

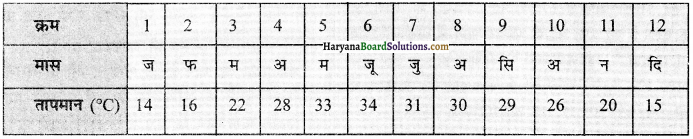
उत्तर:
तापमान के आँकड़ों को आरोही या अवरोही क्रम –


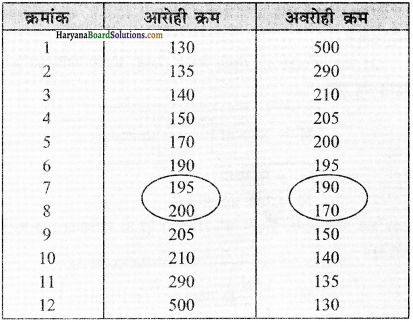
माध्यिका (M) = \(\frac {N+1}{2}\) वीं मद = \(\frac {12+1}{2}\) = 6.5 वीं मद
6.5 वीं मद का आकार = \(\frac {6वीं मद + 7वीं मद}{2}\) = \(\frac{26+28}{2}=\frac{54}{2}\) = 27°C

प्रश्न 13.
माध्यिका के गुण-दोष बताओ।
उत्तर:
माध्यिका के गुण (Merits) –
1. सरल विधि-माध्यिका ज्ञात करना एक सरल विधि है।
2. चरम मूल्यों का निम्नतम प्रभाव-माध्यिका चरम मूल्यों से प्रभावित नहीं होती है।
3. आँकड़ों के अभाव में प्रयोग-अपूर्ण आँकड़ों के बावजूद इसकी गणना की जा सकती है।
4. खुले सिरे वाली शृंखला में उपयोग-खुले सिरे वाली शृंखला में माध्यिका का मूल्य सुगमता से प्राप्त हो जाता है।
5. ग्राफिक विधि-माध्यिका का मूल्य ग्राफ की सहायता से भी ज्ञात किया जा सकता है।
6. निश्चित मूल्य-माध्यिका का मूल्य सदैव निश्चित होता है।
7. माध्यिका शृंखला के मूल्यों का प्रतिनिधि होता है। यह संपूर्ण बंटन के लिए गुरुत्व का केन्द्र होता है। यह गुणात्मक तथ्यों (सुन्दरता, ईमानदारी आदि) का अध्ययन करने के लिए सर्वोत्तम है।

माध्यिका के दोष (Demerits) –
(1) समंकों को आरोही तथा अवरोही क्रम में रखना आवश्यक है जिस पर अधिक समय लगता है।
(2) माध्यिका श्रेणी के सभी मूल्यों पर आधारित नहीं होती। यह केवल अनुमानित तथा स्थिति संबंधी माध्य है।
(3) यह एक उपयुक्त माध्य नहीं है क्योंकि यह चरम मूल्यों से प्रभावित नहीं होती।
(4) सम संख्याओं की दशा में यह दो संख्याओं के मध्य एक अनुमानित संख्या होती है।
(5) यह अनियमित आँकड़ों के लिए उपयुक्त विधि नहीं है।
(6) अधिक आँकड़े होने पर माध्यिका ज्ञात करना कठिन होता है।

प्रश्न 14.
बहुलक (Mode) किसे कहते हैं ? इसे किस प्रकार ज्ञात किया जाता है ? उसके गुण-दोष बताओ।
उत्तर:
बहुलक (Mode) – आँकड़ों का वह मूल्य है जो सबसे अधिक बार आता है, बहुलक कहलाता है। इस विशेष मान के चारों ओर आँकड़ों का सबसे अधिक संकेंद्रण होता है। यह मूल्य श्रेणी का प्रतिनिधि मूल्य है तथा सबसे अधिक लोकप्रिय होता है। निरीक्षण विधि (Inspection Method) द्वारा बहुलक ज्ञात करने की विधि-इस विधि में यह निश्चित करना पड़ता है कि कौन-सा मद सबसे अधिक बार आ रहा है अर्थात् जिस मूल्य की आवृत्ति सबसे अधिक होती है उसे बहुलक कहते हैं। जब खंडित श्रेणी की आवृत्तियां नियमित रूप से बढ़ती या घटती हैं तो अधिकतम आवृत्ति बिल्कुल स्पष्ट हो जाती है।

उदाहरण:

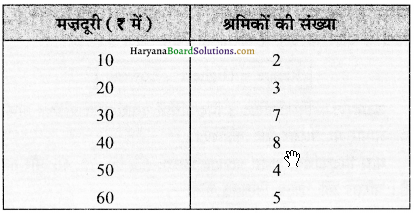
उपर्युक्त श्रृंखला से स्पष्ट है कि ₹ 40 की आवृत्ति 8 है जो सबसे अधिक है। इसलिए बहुलक (Z = ₹ 40) है।
उदाहरण:
निम्नलिखित बंटन से बहुलक ज्ञात करें। 2,10,5,7,9,2,7,11,17,7,8 बहुलक का मान निम्नलिखित चरणों में प्राप्त किया जा सकता है –

चरण 1.
आँकड़ों को आरोही या अवरोही क्रम में व्यवस्थित करके सारणीबद्ध करो।

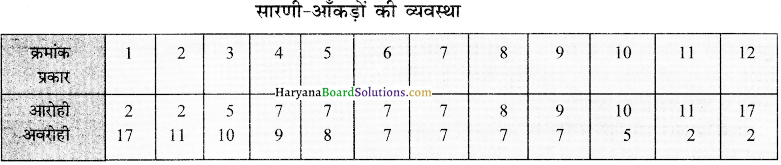
चरण 2.
आरोही एवं अवरोही दोनों ही क्रमों में ‘ 7 ‘ का मान सबसे अधिक बार अर्थात् 3 बार आता है।
अत: बहुलक =7
बहुलक के गुण (Merits) –
(1) बहुलक की गणना सरलता से निरीक्षण विधि द्वारा की जा सकती है।
(2) बहुलक पर शृंखला के चरम मूल्यों का प्रभाव नहीं पड़ता।
(3) किसी शृंखला में सबसे अधिक बार आने के कारण, यह उसका सर्वोत्तम प्रतिनिधि होता है।
(4) अंकों के अभाव की हालत में भी बहुलक ज्ञात किया जा सकता है।
(5) बहुलक की व्यावहारिक उपयोगिता अधिक है। किसी वस्तु की अधिक मात्रा के कारण उसका उत्पादन अधिक होता है।
(6) बहुलक को रेखाचित्र द्वारा भी प्रदर्शित करके इसे सरल रूप दिया जा सकता है।

बहुलक के दोष (Demerits) –
(1) दो से अधिक समंकों की बारंबारता समान होने के कारण, बहुलक एक अनिश्चित व अस्पष्ट माध्य है।
(2) बहुलक सभी मदों पर आधारित नहीं होता।
(3) बहुलक कभी-कभी असत्य और भ्रमात्मक भी हो सकता है।
(4) बहुलक ज्ञात करने में चरम मूल्यों पर ध्यान नहीं दिया जाता।
(5) अधिक संख्याएं न होने पर बहुलक एक महत्त्वपूर्ण माप नहीं है।
(6) वर्ग विस्तार बदलने पर बहुलक भी बदल जाता है।

प्रश्न 15.
विचलन की माप क्या है ? इसके प्रकार बताओ।
उत्तर:
विचलन की माप (Measures of Deviation) –
विचलन या विक्षेपण का सामान्य अर्थ चरों का एक केंद्रीय मान से बिखराव या विभिन्नता होता है। विचलन के चार वैकल्पिक मानों को हम लेंगे –
(1) परिसर (Range)
(2) माध्य विचलन (Mean Deviation)
(3) मानक विचलन (Standard Deviation)
(4) चतुर्थक विचलन (Quartile Deviation)

प्रश्न 16.
परिसर से क्या भाव है ? उदाहरण सहित स्पष्ट करो कि माध्य विचलन कैसे ज्ञात किया जाता है ?
उत्तर:
परिसर (Range) –
परिवर्तनशीलता का सबसे सरल माप परिसर है। यह माप किसी शृंखला में अधिकतम $(\mathrm{H})$ एवं न्यूनतम $(\mathrm{L})$ मानों में अंतर के रूप में परिभाषित किया जाता है।
Range = Highest – Lowest

उदाहरण:
निम्नलिखित 5 विद्यार्थियों द्वारा प्राप्त प्रतिशत अंकों के आधार पर परिसर ज्ञात कीजिए। पांच विद्यार्थियों द्वारा प्राप्तांक क्रमशः $83,96,72,46$ और 68 है। परिसर की गणना निम्नवत् होगी –
चरण 1. (Step 1) –
दिए ग़ए उदाहरण में अधिकतम (H) एवं न्यूनतम (L) को ज्ञात करें।
H = 96
L = 46

चरण 2. (Step 2) –
निम्नलिखित सूत्र का प्रयोग कर हम परिसर की गणना करेंगे-
R = H – L
R = 96 – 46 = 50%
परिसर विचलन की माप का अपरिष्कृत (Crude) मापन है क्योंकि इसमें परिसर के अंतर्गत मानों के वितरण (बंटन) के स्वरूप की कोई सूचना उपलब्ध नहीं होती। परिसर ज्ञात करना आसान है क्योंकि यह केवल दो चरम अंकों पर आधारित है।

माध्य विचलन एवं निरपेक्ष वितरण (Mean Deviation) –
माध्य विचलन (MD) माध्य (X) से निरपेक्ष विचलन (उनके चिह्नों ±) पर ध्यान दिए बिना) होता है। गणितीय सूत्र के रूप में माध्य विचलन (MD) को निम्नवत लिखा जा सकता है –
M.D = \(\frac{\sum|x-\bar{x}|}{N}\)
जहां
x = जनसंख्या का कोई मान
\(\bar{x}\) = जनसंख्या का माध्य
N = जनसंख्या की कुल संख्या

माध्य विचलन एक वैज्ञानिक माप है क्योंकि यह समांतर माध्य से विभिन्न मानों के बीच विचलनों का औसत है। उदाहरण-निम्नलिखित जनसंख्या के लिए माध्य विचलन की गणना कीजिए –
6,8,4,12,5
माध्य विचलन की गणना निम्नवत करते हैं –
(1) सभी मदों को (X) मान लो।
(2) समांतर माध्य \(((\overline{\mathrm{X}})\) ज्ञात करो।
(3) प्रत्येक मद में से \(\overline{\mathrm{X}}\) घटाओ। \((\mathrm{X}-\overline{\mathrm{X}}=d)\)
(4) प्रत्येक विचलन को जोड़ कर ∑d ज्ञात करें।
(5) विचलनों के योग को मदों की संख्या (N) से भाग दो।

चरण (Step) 1.
औसत माध्य \(((\overline{\mathrm{X}})\) की गणना कीजिए –
\(((\overline{\mathrm{X}})\) (अंकिक माध्य) = \(\frac{6+8+4+12+5}{5}\) = \(\frac{35}{5}\)= 7

चरण (Step) 2.
सारणी स्वरूप में प्रत्येक चर अंक में से माध्य मान को घटाइए –

चरण (Step) 3. अत: निरपेक्ष माध्य विचलन होगा
= \(\frac{1}{N} \Sigma|X \pm \bar{X}|=\frac{12}{5}\) = \(\frac{\sum|X-\bar{X}|}{N}=\frac{12}{5}\) = 2.4

प्रश्न 17.
मानक विचलन तथा चतुर्थक विचलन से क्या अभिप्राय है ? इन्हें ज्ञात करने की विधि बताओ।
उत्तर:
मानक विचलन (Standard Deviation) –
विचलन के माप की दूसरी विधि, जो औसत माध्य [(A.M. (7)] का प्रयोग कर प्राप्त की जाती है मानक विचलन (σ) कहलाती है। इसे वर्ग माध्य-मूल विचलन भी कहते हैं। मानक विचलन किसी श्रेणी के विभिन्न मूल्यों के समांतर माध्य से निकाले गए विचलनों के वर्गों के माध्य का वर्गमूल होता है। इसे ग्रीक भाषा के अक्षर (σ) सिग्मा से प्रकट किया जाता है। गणितीय सूत्र में इसे निम्नवत रखा जाता है –
\(\left.\underset{(\text { सिग्मा) }}{\sigma}=\sqrt{\left[\Sigma{ }^{(\mathrm{X}-\overline{\mathrm{X}})^2}\right.}\right]\)

उदाहरण:
निम्नलिखित बंटन का मानक विचलन ज्ञात करें।
6,8,4,2,5
मानक विचलन की गणना निम्न चरणों में होगी –

चरण (Step) 1.
औसत माध्य A.M. \((\overline{\mathrm{X}})\) ज्ञात करें –
\((\overline{\mathrm{X}})\) = \(\frac{6+8+4+2+5}{5}\) = \(\frac{25}{5}\) = 5

चरण (Step) 2.
सारणी स्वरूप में A.M. से वर्ग विचलन का निर्धारण करें।

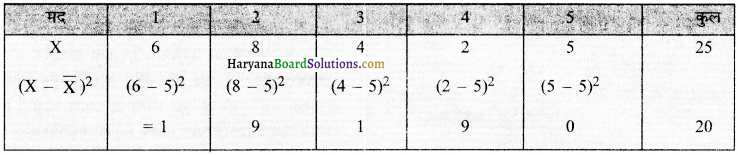
इसलिए
σ = \(\sqrt{\frac{20}{5}}\) = \(\sqrt{4}\) = 2
इस प्रकार उपरोक्त बंटन का मानक विचलन σ = 2 होगा।

चतुर्थक विचलन (Q.D.) (Quartile Deviation) –
माध्यिका द्वारा संपूर्ण बंटन दो बराबर भागों में विभक्त होता है किंतु चतुर्थक द्वारा संपूर्ण बंटक चार बराबर भागों में विभक्त करता है। चतुर्थक वह मूल्य है जो किसी श्रेणी को चार समान भागों में बांटता है इसे विभाजन मूल्य (Partition Value) कहते हैं। किसी भी श्रेणी में तीन चतुर्थक होते हैं।
(1) Q₁ = पहला चतुर्थक या न्यून चतुर्थक (The Lower Quartile)
(2) Q₂ = दूसरा चतुर्थक या मध्य चतुर्थक (The Middle Quartile)
(3) Q₃ = तीसरा चतुर्थक या ऊपरी चतुर्थक (The Upper Quartile)

(i) न्यून चतुर्थक (Q₁) –
यह कुल बंटन का \(\frac{1}{4}\) या एक चौथाई भाग इससे कम होगा जबकि कुल बंटन का \(\frac{3}{4}\) भाग इसके ऊपर या अधिक होगा।

(ii) मध्य चतुर्थक (Q₂) – इस प्रकार कुल बंटन का \(\frac{1}{2}\) होगा जिसमें आधा भाग इसके नीचे व शेष आधा इसके ऊपर या अधिक होगा। इस प्रकार मध्य चतुर्थक (Q₂) – कुछ नहीं बल्कि माध्यिका ही होता है।

(iii) ऊपरी चतुर्थक (Q₃) – शृंखला को इस प्रकार बांटता है कि \(\frac{3}{4}\) भाग इससे नीचे तथा केवल \(\frac{1}{4}\) भाग इसके ऊपर या अधिक होता है। चतुर्थक विचलन Q.D. को अन्तचतुर्थक का परिसर भी कहा जाता है, जिसे निम्नवत प्रदर्शित करते हैं-
Q.D = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}\)
उदाहरण:
उदाहरण-निम्नलिखित बंटन के लिए चतुर्थक विचलन का निर्धारण कीजिए –
46,32,25,50,72,35,75,65 तथा 58

चतुर्थक विचलन को निम्नवत निर्धारित किया जाता है –

चरण (Step) 1.
बंटन को आरोही क्रम में व्यवस्थित करें तथा उन्हें क्रमानुसार कोटि प्रदान करें जैसा कि नीचे दिया गया है- 25
32,35,46,50,58,65,72,75

चरण (Step) 2.
मध्य चतुर्थक (Q₂) अथवा माध्यिका (Mc) सही-सही माध्य की संख्या है। जैसे-
\(\frac{n+1}{2}=\frac{9+1}{2}\) = 5वीं (चूंकि n = 9)

चरण (Step) 3.
निम्न चतुर्थक (Q₃) निम्न आद्धर्ध (Mc) का आधा होता है, जैसे कि
\(\frac{5}{2}\) = 2.5 वीं संख्या
∴ Q₁ = \(\frac{32+35}{2}=\frac{67}{2}\) = 33.5

चरण (Step) 4.
ऊपरी चतुर्थक Q₃ उत्तरार्ध का आधा होता है। जैसे कि
\(\frac{7+8}{2}\) = 7.5 वीं संख्या
∴ Q₃ = \(\frac{65+72}{2}=\frac{137}{2}\) = 68.5

चरण (Step) 5.
चतुर्थक विचलन की गणना निम्नसूत्र Q.D. द्वारा की जाती है।
Q.D = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}\) = \(\frac{68.5-33.5}{2}\) = \(\frac{35}{2}\) = 17.5

प्रश्न 18.
सह-संबंध से क्या अभिप्राय है ? सह-संबंध गुणांक की गणना कैसे की जाती है ?
उत्तर:
सहसंबंध (Correlation) –
दो भिन्न प्रकार के चरों के एक बंटन को द्विचरीय वितरण कहते हैं, ये दोनों चर उस अवस्था में आपस में सह-संबंधित कहलाते हैं जब एक चर में परिवर्तन दूसरे चर में संगती परिवर्तन उत्पन्न होता है। प्रथम चर जिसके कारण दूसरे चर में परिवर्तन होता है स्वतंत्र (x) कहलाता है जबकि दूसरा चर आश्रित चर (y) के रूप में जाना जाता है। दो चरों के मध्य साहचर्य की मात्रा तथा दिशा का आंकलन सरल अथवा द्विचर सह-संबंध कहलाता है। सह-संबंध की माप का सर्वाधिक प्रचलित स्वरूप पियर्सन का गुणन आघूर्ण सह-संबंध गुणांक (r) है। r का मूल्य +1 से -1 के बीच प्रसारित होता है।

इस प्रकार जब –
(i) r +1 हो तो सहसंबंध पूर्ण तथा धनात्मक होता है,
(ii) r = 0 हो तो कोई सह-संबंध नहीं या शून्य सहसंबंध, तथा
(iii) r = -1 हो तो सह-संबंध ऋणात्मक होता है।
गुणन आघूर्ण सह-सम्बन्ध गुणांक (r) को गणितीय सूत्र में निम्नवत लिखा जाता है –
r = \(\frac{N \Sigma x y-\Sigma x, \Sigma y}{\sqrt{\left[N \Sigma x^2-(\Sigma x)^2\right]}\left[N \Sigma y^2-(\Sigma y)^2\right]}\)

जिसमें
x = स्वतंत्र चर
y = आश्रित चर
N = बंटन की कुल संख्या है

उदाहरण:
निम्नलिखित आँकड़ों “खखेत का आकार और विक्रय मूल्य” के आधार पर पियर्सन सह-संबंध गुणांक की गणना करें।

अग्रवत सारणी रूप में पियर्सन के सह-संबंध गुणांक की गणना की जा सकती है।
चरण (Step) 1.
दोनों चरों को अलग-अलग प्रदर्शित करते हुए आँकड़ों को क्रमानुसार व्यवस्थित करें व फिर उन्हें अलग-अलग जोड़ें।

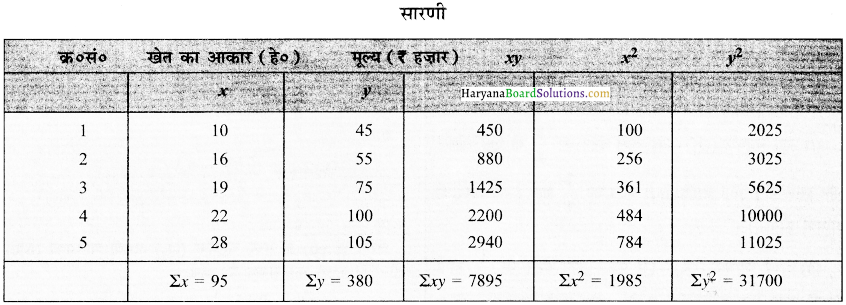
चरण (Step) 2.
x को y से गुणा करें व फिर उन्हें जोड़ें, इस प्रकार, ∑x = 95, ∑y = 380, ∑x y = 7895 होगा तथा ∑x^-2 = 1985 व ∑y² = 31700 होगा

चरण (Step) 3.
सूत्र का प्रयोग कर पियर्सन के गुणक आघूर्ण सहसंबंध गुणांक की गणना करते हैं।
r = \(\frac{N \Sigma x y-\Sigma x \Sigma y}{\sqrt{\left[N \Sigma x^2-(\Sigma x)^2\right]\left[N \Sigma y^2-(\Sigma y)^2\right]}}\)
r = \(\frac{5 \times 7895-95 \times 380}{\sqrt{\left[5 \times 1985-(95)^2\right]\left[5 \times 31700-(380)^2\right]}}\)
r = \(\frac{39475-36100}{\sqrt{(9925-9325)(158900-144400)}}\)
= \(\frac{3375}{356230}\) = + 0.95
इस प्रकार यह कहा जा सकता है कि “भूमि का मूल्य खेत के आकार के सशक्त एवं प्रत्यक्ष रूप से सहसंबंधित हैं।” सारणी स्वरूप में और माध्य से वर्ग विचलन ज्ञात करें-

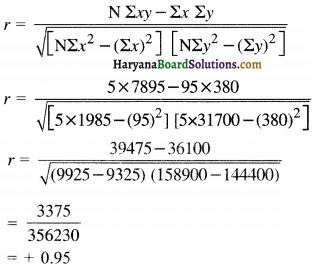
प्रश्न 19.
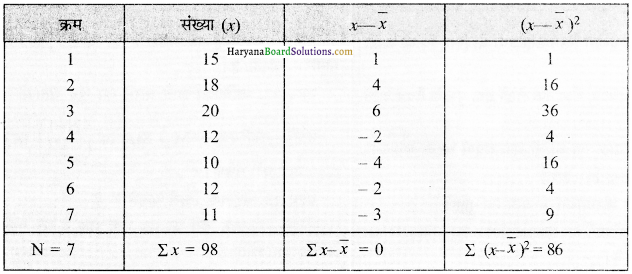
दिए गए आँकड़ों की सहायता से मानक विचलन की गणना कीजिए।
15,18,20,12,10,12,11
उत्तर:
औसत माध्य \((\overline{\mathrm{X}})\)
ज्ञात करो – \((\overline{\mathrm{X}})\) = \(\frac{\sum x}{N}\)
\((\overline{\mathrm{X}})\) = \(\frac{15+18+20+12+10+12+11}{7}\)= \(\frac{98}{7}\) = 14m

मानक विचलन
(S.D) (σ) = \(\sqrt{\frac{\Sigma(x-\bar{x})^2}{N}}\) = \(\sqrt{\frac{86}{7}}=\sqrt{12.28}\) = 3.5

प्रश्न 20.
निम्न सारणी में शिक्षकों तथा विद्यार्थियों के बीच संबंध को दर्शाया गया है। शिक्षकों व विद्यार्थियों के बीच सहसंबंध प्रकृति ज्ञात कीजिए।

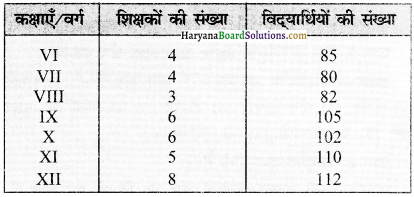
उत्तर:
चरण 1-दोनों चरों को अलग-अलग प्रदर्शित करते हुए X को Y से गुणा करें।

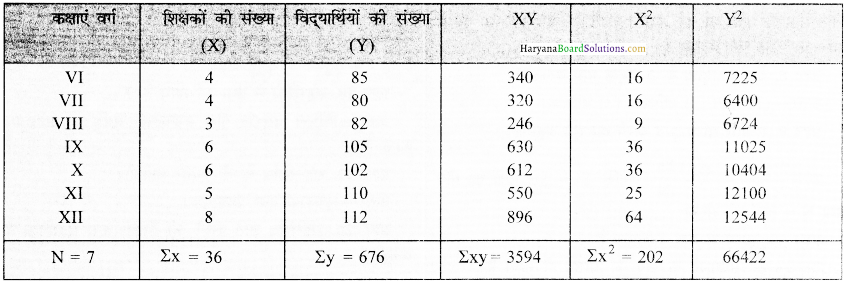
सहसंबंध गुणांक

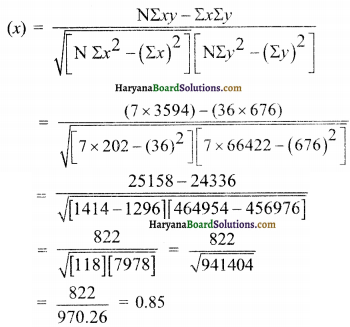
मौखिक परीक्षा के प्रश्न (Questions For Viva-Voce)

प्रश्न 1.
आँकड़ों का प्रयोग किन उद्देश्यों के लिए किया जाता है ?
उत्तर:
मानचित्र, प्रतिवेदन, वैज्ञानिक लेखों तथा पुस्तकें तैयार करने के लिए।

प्रश्न 2.
आँकड़ों के प्रक्रमण के दो महत्त्वपूर्ण घटक बताओ।
उत्तर:
सारणीयन तथा विश्लेषण।

प्रश्न 3.
आँकड़ों के सारणीयन से क्या अभिप्राय है ?
उत्तर:
सारणीयन आँकड़ों को एक व्यवस्थित तथा क्रमबद्ध रूप में प्रस्तुत करने की विधि है।

प्रश्न 4.
एक अच्छी सारणी के क्या गुण होते हैं ?
उत्तर:
सरल, सघन, पूर्ण तथा स्वयं विश्लेषणात्मक होना।

प्रश्न 5.
एक सारणी के प्रमुख क्रियात्मक अंग बताओ।
उत्तर:
सांख्यिकीय सारणी के 8 अंग होते हैं –
(1) संख्या
(2) शीर्षक
(3) शीर्ष-टिप्पणी
(4) प्रतिपर्ण
(5) कक्ष-शीर्ष
(6) मुख्य भाग
(7) पाद-टिप्पणी
(8) स्रोत-टिप्पणी।

प्रश्न 6.
आवृत्ति क्या होती है ?
उत्तर:
किसी शृंखला-श्रेणी में कोई मद कितनी बार आती है, उसे उस पद की आवृत्ति कहते हैं।

प्रश्न 7.
वर्ग अंतराल किसे कहते हैं ?
उत्तर:
आँकड़ों को वर्ग में बांट देने के पश्चात् उनकी ऊपरी तथा निम्न सीमा के अंतर को वर्ग अंतराल कहते हैं-जैसे 30-40 वर्ग में 40-30 =10 वर्ग अंतराल है।

प्रश्न 8.
केंद्रीय प्रवृत्ति के 3 प्रमुख माप बताओ।
उत्तर:
(1) माध्य
(2) माध्यिका
(3) बहुलक।

प्रश्न 9.
समांतर माध्य ज्ञात करने का सूत्र बताओ।
उत्तर:
माध्य \(=\overline{\mathrm{X}}=\frac{\Sigma \mathrm{x}}{\mathrm{N}}\) जबकि \(\Sigma \mathrm{x}=\) कुल मानों का योग तथा N = मानों की संख्या

प्रश्न 10.
माध्य से क्या अभिप्राय है ?
उत्तर:
कई संख्याओं के योग का औसत ही माध्य है।

प्रश्न 11.
माध्यिका से क्या अभिप्राय है ?
उत्तर:
माध्यिका वह संख्या है जो किसी शृंखला को दो बराबर भागों में बांटती है।

प्रश्न 12.
माध्यिका ज्ञात करने का सूत्र बताओ।
उत्तर:
माध्यिका = M = N Size Of \(\left(\frac{\mathrm{N}+1}{2}\right)\) th item जबकि N = मदों की संख्या।

प्रश्न 13.
बहुलक किसे कहते हैं ?
उत्तर:
बहुलक चरों का वह मान होता है जो शृंखला में सबसे अधिक बार आता है।

प्रश्न 14.
माध्य विचलन किसे कहते हैं ?
उत्तर:
माध्य विचलन माध्य से निरपेक्ष विचलन होता है।

प्रश्न 15.
माध्य विचलन ज्ञात करने का सूत्र बताओ।
उत्तर:
माध्य विचलन = M.D. = \(\frac{\Sigma(\mathrm{x}-\overline{\mathrm{x}})}{\mathrm{N}}\)
X = संख्या
X = माध्य
N = मदों की संख्या।

प्रश्न 16.
मानक विचलन किसे कहते हैं ?
उत्तर:
विचलनों के वर्गों के माध्य के वर्ग मूल को मानक विचलन कहते हैं।

प्रश्न 17.
चतुर्थक विचलन (Q.D.) से क्या अभिप्राय है ?
उत्तर:
जब संपूर्ण बंटन को चार बराबर भागों में विभक्त करते हैं तो उसे चतुर्थक विचलन कहते हैं।

प्रश्न 18.
सहसंबंध से क्या अभिप्राय है ?
उत्तर:
विभिन्न चरों के बीच संख्यात्मक संबंध को सहसंबंध कहते हैं।

प्रश्न 19.
सह-संबंध के दो प्रकार बताओ।
उत्तर:
धनात्मक तथा ऋणात्मक।

प्रश्न 20.
सहसंबंध ज्ञात करने की विधि किस वैज्ञानिक ने बनाई ?
उत्तर:
कार्ल पियर्सन ने।