HBSE 12th Class Chemistry Solutions Chapter 2 विलयन

Haryana State Board HBSE 12th Class Chemistry Solutions Chapter 2 विलयन Textbook Exercise Questions and Answers.

Haryana Board 12th Class Chemistry Solutions Chapter 2 विलयन

प्रश्न 2.1.
विलयन को परिभाषित कीजिए। कितने प्रकार के विभिन्न विलयन संभव हैं? प्रत्येक प्रकार के विलयन के संबंध में एक उदाहरण देकर संक्षेप में लिखिए।
उत्तर:
विलयन (Solution) – दो या दो से अधिक पदार्थों (अवयवों) का समांगी मिश्रण विलयन कहलाता है।
समांगी मिश्रण का अर्थ है कि मिश्रण के सभी भागों का संघटन (composition) तथा गुण समान हैं। विलायक की भौतिक अवस्था के आधार पर विलयन मुख्यतः तीन प्रकार के होते हैं-
(1) गैसीय विलयन
(2) द्रव विलयन
(3) ठोस विलयन |
इन्हें पुनः वर्गीकृत किया जा सकता है जो कि विलेय की भौतिक अवस्था के आधार पर होता है। अतः विलयन वास्तव में 9 प्रकार के होते हैं, जो निम्नलिखित हैं-

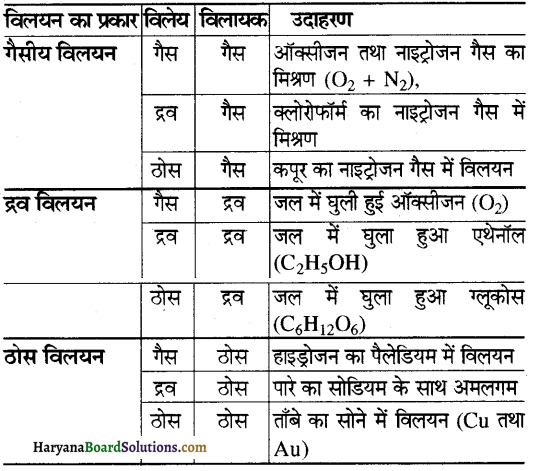
प्रश्न 2.2.
एक ऐसे ठोस विलयन का उदाहरण दीजिए जिसमें विलेय कोई गैस हो ।
उत्तर:
हाइड्रोजन का पैलेडियम में विलयन ।

प्रश्न 2.3.
निम्न पदों को परिभाषित कीजिए-
(i) मोल – अंश
(ii) मोललता
(iii) मोलरता
(iv) द्रव्यमान प्रतिशत ।
उत्तर:
(i) मोल अंश (Mole fraction ) (x) – एक मिश्रण में उपस्थित किसी अवयव का मोल अंश उस अवयव के मोल तथा मिश्रण में उपस्थित सभी अवयवों के कुल मोलों का अनुपात होता है।

(ii) मोललता (Molality) (m) – 1000 g (1 kg) विलायक में घुले हुए विलेय के मोलों की संख्या को उस विलयन की मोललता कहते हैं।

(iii) मोलरता (Molarity) (M) – एक लीटर (1 क्यूबिक डेसीमीटर) विलयन में घुले हुए विलेय के मोलों की संख्या को उस विलयन की मोलरता कहते हैं।

(iv) द्रव्यमान प्रतिशत ( Mass Percentage ) – किसी विलेय के भार भागों की वह संख्या जो विलयन के 100 भार भागों में उपस्थित होती है, उसे द्रव्यमान प्रतिशत कहते हैं।
विलयन में किसी अवयव का द्रव्यमान %

प्रश्न 2.4.
प्रयोगशाला कार्य के लिए प्रयोग में लाया जाने वाला सांद्र नाइट्रिक अम्ल द्रव्यमान की दृष्टि से नाइट्रिक अम्ल का 68% जलीय विलयन है। यदि इस विलयन का घनत्व 1.504 gmL^-1 हो तो अम्ल के इस नमूने की मोलरता क्या होगी ?
उत्तर:
68% (द्रव्यमान) HNO₃ का अर्थ है 68g HNO₃, 100 g विलयन में उपस्थित है।

विलेय ( HNO₃) का भार = 68g HNO₃, विलेय का मोलर द्रव्यमान = 1 + 14 + 48 = 63
विलयन का आयतन = 66.49 ml
∴ M = \(\frac{68 \times 1000}{63 \times 66.49}\)
M = 16.23
अतः HNO₃ के इस नमूने की मोलरता = 16.23 M इसे निम्नलिखित सूत्र द्वारा भी ज्ञात किया जा सकता है-

प्रश्न 2.5.
ग्लूकोस का एक जलीय विलयन 10% (w/w) है । विलयन की मोललता तथा विलयन में प्रत्येक घटक का मोल- अंश क्या है? यदि विलयन का घनत्व 1.2 gmL^-1 हो तो विलयन की मोलरता क्या होगी ?
उत्तर:
10% (w/ w) ग्लूकोस विलयन का अर्थ है कि 10g ग्लूकोस 100g विलयन में उपस्थित है जिसमें 90 ग्राम जल है।
(1) अतः विलयन की मोललता (m)

m = \(\frac{10}{180 \times 90 \times 10^{-3}}\)
मोललता: = 0.617m
यहाँ ग्लूकोस का मोलर द्रव्यमान ( C₆H₁₂O₆) = 180
विलायक की द्रव्यमान = 90g = 90 × 10^-3 kg

(2) ग्लूकोस के मोल = 10/180
जल के मोल = \(\frac { 90 }{ 18 }\) = 5
अतः ग्लूकोस का मोल अंश =
ग्लूकोस का मोल अंश = \(\frac { 0.055 }{ 5.055 }\) = 0.01
अतः जल का मोल अंश = 1 – 0.01 = 0.99
(3)

प्रश्न 2.6.
यदि 1 g मिश्रण में Na₂CO₃ एवं NaHCO₃ के मोलों की संख्या समान हो तो इस मिश्रण से पूर्णतः क्रिया करने के लिए 0.1 M HCl के कितने mL की आवश्यकता होगी ?
उत्तर:
माना 1 g मिश्रण में Na₂CO₃ का द्रव्यमान = x g
Na₂CO₃ का मोलर द्रव्यमान = (2 × 23 ) + 12 + (3 × 16 ) = 106
अतः Na₂CO₃ के मोल (n₁) = \(\frac { x }{ 106 }\) mol
अतः मिश्रण में NaHCO₃ का द्रव्यमान = (1 – x)g
NaHCO₃ का मोलर द्रव्यमान = 23 + 1 + 12 + 48 = 84
अतः NaHCO₃ के मोल (n₂) = \(\frac{1-x}{84}\) mol
Na₂CO₃ तथा NaHCO₃ की HCl से क्रिया के संतुलित समीकरण निम्नलिखित हैं-

चूंकि दिए गए मिश्रण में Na₂CO₃ तथा NaHCO₃ के मोलों की संख्या समान है अतः

Na₂CO₃ तथा NaHCO₃ दोनों से क्रिया के लिए आवश्यक HCl के मोल

यदि आवश्यक HCl का आयतन V है तो
मोलरता × आयतन (L) = मोल
0.1 × V(L) = 0.01578
V (लीटर) = 0.1578 L
अतः HCl का आवश्यक आयतन = 157.8mL

प्रश्न 2.7.
द्रव्यमान की दृष्टि से 25% विलयन के 300g एवं 40% के 400g को आपस में मिलाने पर प्राप्त मिश्रण का द्रव्यमान प्रतिशत सांद्रण निकालिए ।
उत्तर:
25% (w/w), 300 g विलयन में विलेय का भार = (25 × 3) 75g
40% (w/w), 400g विलयन में विलेय का भार = (40 × 4) = 160 g
दोनों विलयनों को मिलाने पर विलेय का कुल भार = 75 + 160 = 235 g
तथा विलयन का कुल भार= 300 + 400 = 700 g
अतः मिश्रण में विलेय का द्रव्यमान

प्रश्न 2.8.
222.6g एथिलीन ग्लाइकॉल, C₂H₄(OH)₂ तथा 200g जल को मिलाकर प्रतिहिम मिश्रण बनाया गया । विलयन की मोललता की गणना कीजिए। यदि विलयन का घनत्व 1.072 g mL^-1 हो तो विलयन की मोलरता निकालिए।
उत्तर:
(i) मोललता (m) =
एथिलीन ग्लाइकॉल (विलेय) का द्रव्यमान = 222.6 g
एथिलीन ग्लाइकॉल [C₂H₄(OH)₂] का मोलर द्रव्यमान = 62
विलायक (जल) का द्रव्यमान = 200g = 0.2 kg
अतः m = \(\frac{222.6}{62 \times 0.2}\) = 17.95 mol Kg^-1

(ii) विलयन की मोलरता

विलयन का कुल द्रव्यमान = 200 + 222.6 = 422.6
विलयन का घनत्व = 1.072 g mL^-1
अतः विलयन का आयतन (V) =

प्रश्न 2.9.
एक पेय जल (drinking water) का नमूना क्लोरोफॉर्म (CHCl₃) से, कैंसरजन्य समझे जाने की सीमा तक बहुत अधिक संदूषित (Contaminated) है। इसमें संदूषण की सीमा 15 ppm (द्रव्यमान में ) है –
(i) इसे द्रव्यमान प्रतिशत में व्यक्त कीजिए ।
(ii) जल के नमूने में क्लोरोफॉर्म की मोललता ज्ञात कीजिए ।
उत्तर:
(i) 15 ppm CHCl₃ का अर्थ है कि 10⁶ भाग विलयन में 15 भाग CHCl₃ है।
अतः विलेय का द्रव्यमान (भार) = 15 g
विलयन का द्रव्यमान = 10⁶ g

द्रव्यमान % = \(\frac{15 \times 100}{10^6}\) = 15 × 10^-4 = 1.5 × 10^-3%

(ii) विलायक का द्रव्यमान = विलयन का द्रव्यमान – विलेय का द्रव्यमान
= 10⁶ – 15 = 999985g
= 9.99985 × 10⁵
विलयन की मोललता (m)

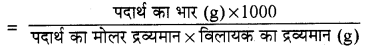
CHCl₃ का मोलर द्रव्यमान = 12 + 1 + (3 × 35.5)
= 119.5 g mol^-1

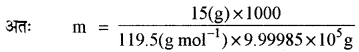
m = 0.0125 × 10^-2
m = 1.25 x 10^-4
अतः जल के नमूने में CHCl₃ की मोललता = 1.25 x 10^-4 m

प्रश्न 2.10.
ऐल्कोहॉल एवं जल के एक विलयन में आण्विक अन्योन्य क्रिया (Molecular Interaction) की क्या भूमिका है?
उत्तर:
ऐल्कोहॉल एवं जल का विलयन धनात्मक विचलन दर्शाता है। क्योंकि ऐल्कोहॉल तथा जल दोनों में अन्तराअणुक हाइड्रोजन बन्ध होते हैं। लेकिन दोनों को मिलाने पर ऐल्कोहॉल तथा जल के मध्य बना हाइड्रोजन बन्ध, शुद्ध जल के हाइड्रोजन बन्ध की तुलना में दुर्बल होता है।
अतः इस विलयन के लिए △H(मिश्रण) = +ve तथा △V (मिश्रण) = +ve होंगे। अतः मिश्रण का वाष्प दाब अधिक होगा तथा क्वथनांक कम होगा। इसलिए यह राउल्ट के नियम से धनात्मक विचलन का उदाहरण है।

प्रश्न 2.11.
ताप बढ़ाने पर गैसों की द्रवों में विलेयता में, हमेशा कमी आने की प्रवृत्ति क्यों होती है ?
उत्तर:
ताप बढ़ाने पर गैसों की द्रवों में विलेयता कम होती है क्योंकि घोले जाने पर गैसों के अणु द्रव प्रावस्था में विलीन होकर उसमें उपस्थित होते हैं अतः यह संघनन अभिक्रिया के समान है तथा इस प्रकिया में ऊष्मा उत्सर्जित (ऊष्माक्षेपी प्रक्रम) होती है। गैसों की द्रव में विलेयता गतिक साम्य है अतः ले – शातैलिए के नियम के अनुसार ताप बढ़ने पर विलेयता घटेगी अर्थात् साम्य पश्च दिशा में जाएगा।

प्रश्न 2.12.
हेनरी का नियम तथा इसके कुछ महत्वपूर्ण अनुप्रयोग लिखिए।
उत्तर:
हेनरी का नियम-
(i) स्थिर ताप पर किसी गैस की द्रव में विलेयता, उस गैस के दाब के समानुपाती होती है। किसी द्रवीय विलयन में गैस की विलेयता गैस के आंशिक द पर निर्भर करती है तथा विलयन में गैस की विलेयता को मोल अंश में व्यक्त किया जाता है।

(ii) किसी विलयन में गैस का मोल अंश, उस विलयन के ऊपर उपस्थित गैस के आंशिक दाब के समानुपाती होता है ।

(iii) किसी गैस का वाष्प अवस्था में आंशिक दाब (p), उस विलयन में गैस के मोल अंश (x) के समानुपाती होता है।
p = K_HX जहाँ K_H = हेनरी स्थिरांक
हेनरी के नियम के महत्वपूर्ण अनुप्रयोग — इसके लिए पाठ्यपुस्तक का भाग संख्या 2.3.2 देखें।

प्रश्न 2.13.
6.56 × 10^-3 g एथेन युक्त एक संतृप्त विलयन में एथेन का आंशिक दाब 1 bar है। यदि विलयन में 5.00 × 10^-2 g एथेन हो तो गैस का आंशिक दाब क्या होगा ?
उत्तर:
हेनरी के नियम के अनुसार p = K_H x
गैस का मोल अंश उसके द्रव्यमान (m) के समानुपाती होता है।
अतः m ∝ x
अतः हेनरी के नियम का वैकल्पिक रूप
m = K_HP

प्रश्न 2.14.
राउल्ट के नियम से धनात्मक एवं ऋणात्मक विचलन का क्या अर्थ है तथा △मिश्रण H के चिह्न इन विचलनों से कैसे सम्बन्धित हैं?
उत्तर:
जब कोई विलयन सभी सांद्रताओं पर राउल्ट के नियम का पालन नहीं करता तो वह अनादर्श विलयन (Non Ideal Solution) कहलाता है। इन विलयनों का वाष्पदाब राउल्ट के नियम द्वारा परिकलित किए गए वाष्प दाब से या तो अधिक होता है या कम । यदि यह अधिक होता है तो राउल्ट नियम से धनात्मक विचलन प्रदर्शित करता है और यदि यह कम होता है तो ऋणात्मक विचलन प्रदर्शित करता है।

प्रश्न 2.15.
विलायक के सामान्य क्वथनांक पर एक अवाष्पशील विलेय के 2% जलीय विलयन का 1.004 bar वाष्प है । विलेय का मोलर द्रव्यमान क्या है?
उत्तर:
शुद्ध जल का वाष्प दाब (p₁⁰) = 1.013 bar होता है।
विलयन का वाष्प दाब (p₁) = 1.004 bar
विलेय का 2% जलीय विलयन है अतः
W₂ = 2 gm तथा (W₁+ W2) = 100g.
W₁ = 98g

प्रश्न 2.16.
हेप्टेन एवं ऑक्टेन एक आदर्श विलयन बनाते हैं। 373 K पर दोनों द्रव घटकों के वाष्प दाब क्रमश: 105.2 kPa तथा 46.8 kPa हैं। 26.0g हेप्टेन एवं 35.0g ऑक्टेन के मिश्रण का वाष्प दाब क्या होगा ?
उत्तर:
हेप्टेन (C₇H₁₆) का मोलर द्रव्यमान = (7 × 12) + 16 = 100
ऑक्टेन का मोलर द्रव्यमान ( C₈H₁₈ ) = (8 × 12 ) +18 = 114
हेप्टेन के मोल (n₁) = \(\frac { 26 }{ 100 }\) = 0.26
ऑक्टेन के मोल (n₂) = \(\frac { 35 }{ 114 }\) = 0.307
हेप्टेन की मोल भिन्न (x₁) = \(\frac{0.26}{0.26+0.307}\)
x₁ = \(\frac{0.26}{0.567}\) = 0.458

ऑक्टेन की मोल भिन्न (x₂) = 1 – x₁
= 1 – 458 = 0.542
विलयन में हेप्टेन का वाष्प दाब (P₁) = P₁⁰x₁
= 105.2 × 0.458 (P₁⁰ = 105.2k Pa) = 48.18 kPa

विलयन में ऑक्टेन का वाष्प दाब (P2) = P₂⁰x2
P2 = 46.8 × 0.542 = 25.36kPa (p) (P⁰₂ = 46.8k Pa)

मिश्रण का कुल वाष्प दाब (p) = P₁ + P₂
p = 48.18 + 25.36
p = 73.54 kPa

प्रश्न 2.17.
300K पर जल का वाष्प दाब 12.3 kPa है। इसमें बने अवाष्पशील विलेय के एक मोलल विलयन का वाष्प दाब ज्ञात कीजिए ।
उत्तर:
शुद्ध जल का वाष्प दाब p1⁰ (H₂O) = 12.3kPa
चूंकि 1 मोलल विलयन है अतः विलेय के मोल (n₂) = 1 मोल
विलायक (H₂O) के मोल (n₁) = \(\frac { 1000 }{ 18 }\) = 55.5
जल की मोल भिन्न (x₁) = \(\frac { 55.5 }{ 55.5 + 1 }\) = 0.982
विलयन का वाष्प दाब (P₁) = x₁ × P₁⁰
P₁ = 0.982 × 12.3
P₁ = 12.08 k Pa
अतः विलयन का वाष्प दाब = 12.08 pk Pa

प्रश्न 2.18
114 g ऑक्टेन में किसी अवाष्पशील विलेय (मोलर द्रव्यमान 40 g mol^-1) की कितनी मात्रा घोली जाए कि ऑक्टेन का वाष्प दाब घट कर मूल का 80% रह जाए ?
उत्तर:
विलयन का वाष्प दाब (P₁) = P₁⁰ का 80% है।
अतः P1 = P1⁰ × 0.8
माना विलेय का द्रव्यमान = w g,
मोलर द्रव्यमान = 40g mol^-1
विलेय के मोल = \(\frac { w }{ 40 }\)
ऑक्टेन (C₈H₁₈) का मोलर द्रव्यमान = 114 g mol^-1
विलेय का द्रव्यमान = 114 g
ऑक्टेन (विलायक) के मोल = \(\frac { 114 }{ 114 }\) = 1 mol
विलेय की मोल भिन्न (x₂)

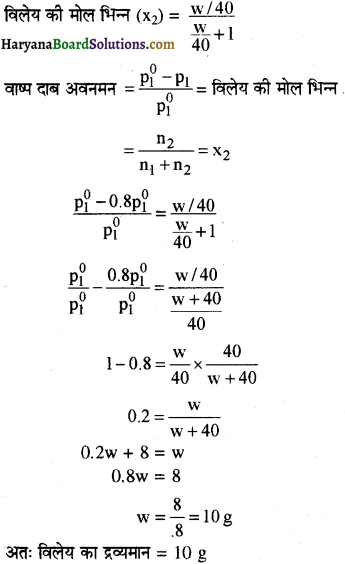
प्रश्न 2.19.
एक विलयन जिसे एक अवाष्पशील ठोस के 30g को 90g जल में विलीन करके बनाया गया है। उसका 298K पर वाष्प दाब 2.8 kPa है । विलयन में 18 g जल और मिलाया जाता है जिससे नया वाष्प दाब 298K पर 2.9 kPa हो जाता है। निम्नलिखित की गणना कीजिए-
(i) विलेय का मोलर द्रव्यमान
(ii) 298 K पर जल का वाष्प दाब।
उत्तर:
(i) विलेय का द्रव्यमान = 30g तथा माना विलेय का मोलर द्रव्यमान = M
अतः विलेय के मोल (n₂) = \(\frac { 30 }{ M }\)
विलायक (H₂O) का द्रव्यमान = 90 g,
मोलर द्रव्यमान: = 18 g mol^-1
अतः विलायक के मोल = \(\frac { 90 }{ 18 }\) = 5
\(\frac{5}{5+(\tilde{3} 0 / \mathrm{M})}\) = \(\frac{5 \mathrm{M}}{5 \mathrm{M}+30}\)
x₁ = \(\frac{M}{6+M}\)
विलयन का आंशिक दाब, P₁ = P₁⁰x₁
2.8 = P₁⁰ × \(\frac{M}{6+M}\) …..(1)

विलयन में 18 g (1 मोल) जल और मिलाया जाता है
तब जल के मोल = 5 + 1 = 6
इस स्थिति में विलायक (H₂O) की मोल भिन्न
x₁ = \(\frac{6}{6+(30 / \mathrm{M})}\) = \(\frac{M}{5+M}\)
विलयन का आंशिक दाब, (P₁¹) = P₀¹x¹₁
2.9 = P₁⁰ × \(\frac{M}{5+M}\) …..(2)
समीकरण (2) में समीकरण (1) का भाग देने पर,
\(\frac { 2.8 }{ 2.9 }\) = \(\frac { 5 + M }{ 6 + M }\)
2.8 (6 + M) = 2.9 (5 + M)
16.8 + 2.8 M = 14.5 + 2.9 M
0.1M = 2.3
M = 23 g mol^-1
अतः विलेय का मोलर द्रव्यमान = 23g mol^-1

(ii) समीकरण (2) में M का मान रखने पर
2.9 = P₁⁰ × \(\frac { 23 }{ 5 + 23 }\)
2.9 = \(\frac{p_1^0 \times 23}{28}\)
23P₁⁰ = 2.9 × 28
23P₁⁰ = 81.2
P₁⁰ = 81.2/23 = 3.53KPa
अतः 298 K पर जल का वाष्प दाब = 3.53 kPa

प्रश्न 2.20
शक्कर के 5% (द्रव्यमान) जलीय विलयन का हिमांक 271K है। यदि शुद्ध जल का हिमांक 273.15K है तो ग्लूकोस के 5% जलीय विलयन के हिमांक की गणना कीजिए ।
उत्तर:
हिमांक अवनमन (△T_f) = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{w}_2 \times 1000}{\mathrm{M}_2 \times \mathrm{w}_1}\)
शक्कर के 5% (द्रव्यमान) विलयन का अर्थ है 5 g शक्कर + 95g H₂O
△T_f = 273.15 – 271 = 2.15
शक्कर का द्रव्यमान (W₂) =5g
W₁ = 95 g.
M₂ = शक्कर का (C₁₂H₂₂O₁₁) मोलर द्रव्यमान = 342
K_f = ?

प्रश्न 2.21.
दो तत्व A एवं B मिलकर AB₂ एवं AB₄ सूत्र वाले दो यौगिक बनाते हैं। 20g बेन्जीन में घोलने पर 1 g AB₂ हिमांक को 2.3K अवनमित ( कम ) करता है। जबकि 1.0g AB₄ से 1.3K का अवनमन होता है। बेन्जीन के लिए मोलर अवनमन स्थिरांक 5.1 K kg mol^-1 है । A एवं B के परमाण्वीय द्रव्यमान की गणना कीजिए ।
उत्तर:
हिमांक अवनमन-
△T_f = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{w}_2 \times 1000}{\mathrm{M}_2 \times \mathrm{w}_1}\)
मोलर द्रव्यमान, M₂ = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{w}_2 \times 1000}{\Delta \mathrm{T}_{\mathrm{f}} \times \mathrm{w}_1}\)
M₂ = M_AB2 = AB₂ का मोलर द्रव्यमान = ?
K_f = 5.1 K kg mol^-1
w₂ = 1g, w₁ = 20g, △T_f = 2.3K
M_AB2 = \(\frac{5.1 \times 1 \times 1000}{2.3 \times 20}\) = 110.869
M_AB2 = 110.87g mol^-1
इसी प्रकार AB₄ का मोलर द्रव्यमान –
M_AB4 = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{w}_2 \times 1000}{\Delta \mathrm{T}_{\mathrm{f}} \times \mathrm{w}_1}\)
△T_f = 1.3K
M_AB4 = \(\frac{5.1 \times 1 \times 1000}{1.3 \times 20}\) = 196.15
M_AB4 = 196.15 g mol^-1
माना x तथा y, A तथा B के परमाणु द्रव्यमान हैं।
तो M_AB2 = x + 2y
110.87 = x +2y …………..(1)
M_AB4 = x + 4y
196.15 = x + 4y
समीकरण ( 2 ) में से समीकरण (1) घटाने पर,
196.15 – 110.87 = 2y
85.28 = 2y
У = 42.64 u

y का मान समीकरण (1) में रखने पर,
110.87 = x + 2 × 42.64
110.87 = x + 85.28
x = 110.87 – 85.28
x = 25.59 u
अतः A का परमाणु द्रव्यमान = 25.59 u तथा
B का परमाणु द्रव्यमान = 42.64 u

प्रश्न 2.22.
300K पर 36 g प्रति लीटर सांद्रता वाले ग्लूकोस के विलयन का परासरण दाब 4.98 bar है। यदि इसी ताप पर विलयन का परासरण दाब 1.52 bar हो तो उसकी सांद्रता क्या होगी ?
उत्तर:
परासरण दाब (Π) = CRT
चूंकि R तथा T नियत हैं अतः
Π ∝ C
अतः किसी पदार्थ के दो विभिन्न सान्द्रता वाले विलयनों के लिए

ग्लूकोस (C₆H₁₂O₆) का मोलर द्रव्यमान = 180
C₁ = \(\frac{36}{180 \times 1}\) = 0.2mol L^-1
अब Π₁ = 4.98bar, Π₂ = 1.52bar
C₁ = 0.2 mol L^-1, C₂ = ?

उपर्युक्त सूत्र में Π₁, Π₂ तथा C₂ का मान रखने पर
\(\frac{4.98}{1.52}\) = \(\frac{0.2}{C_2}\)
C₂ = \(\frac{1.52 \times 0.2}{4.98}\) = 0.061mol L^-1
अतः द्वितीय स्थिति में विलयन की सान्द्रता = 0.061 mol L^-1

प्रश्न 2.23.
निम्नलिखित युग्मों में उपस्थित सबसे महत्वपूर्ण अतंरआण्विक आकर्षण बलों का सुझाव दीजिए-
(i) n – हेक्सेन तथा n – ऑक्टेन
(ii) I₂ तथा CCl₄
(iii) NaClO₄ तथा H₂O
(iv) मेथेनॉल तथा ऐसीटोन
(v) ऐसीटोनाइट्राइल (CH₃CN) तथा ऐसीटोन (C₃H₆O)
उत्तर:
(i) n – हेक्सेन व n ऑक्टेन- ये दोनों ही अध्रुवीय अणु हैं। अतः इनके मध्य वान्डरवाल बल होता है जो कि प्रकीर्णन बल (Dispersion force) या लण्डन बल है। इसे तात्कालिक द्विध्रुव-प्रेरित द्विध्रुव आकर्षण बल भी कहते हैं।

(ii) I₂ तथा CCl₄ के मध्य भी उपर्युक्त प्रकार का वान्डरवाल बल ही पाया जाता है।

(iii) NaClO₄ तथा H₂O के मध्य आयन- द्विध्रुव आकर्षण बल होता है। क्योंकि NaClO₄, Na+ तथा CIO^–₄ में वियोजित हो जाता है।

(iv) मेथेनॉल तथा ऐसीटोन के मध्य द्विध्रुव- द्विध्रुव आकर्षण बल पाया जाता है तथा इनमें कुछ मात्रा में हाइड्रोजन बन्ध भी होता है।

(v) ऐसीटोनाइट्राइल (CH₃CN) तथा ऐसीटोन (CH₃COCH₃) के मध्य भी द्विध्रुव-द्विध्रुव आकर्षण बल होता है।

प्रश्न 2.24.
विलेय-विलायक आकर्षण के आधार पर निम्नलिखित को n ऑक्टेन में विलेयता के बढ़ते क्रम में व्यवस्थित कीजिए – KCI, CH₃OH, CH₃CN, साइक्लोहेक्सेन ।
उत्तर:
n- ऑक्टेन, अध्रुवीय विलायक है अतः विलेयता के सामान्य सिद्धान्त “समान, समान को घोलता है,” के अनुसार जब विलेय की ध्रुवता कम होगी तो n – ऑक्टेन में उसकी विलेयता बढ़ेगी। अतः उपर्युक्त यौगिकों की n – ऑक्टेन में विलेयता का बढ़ता क्रम निम्न प्रकार होगा-
KCI < CH₃OH < CH₃CN < साइक्लोहेक्सेन

प्रश्न 2.25.
पहचानिए कि निम्नलिखित यौगिकों में से कौनसे जल में अत्यधिक विलेय, आंशिक रूप से विलेय तथा अविलेय हैं-
(i) फीनॉल
(ii) टॉलूईन
(iii) फार्मिक अम्ल
(iv) एथिलीन ग्लाइकॉल
(v) क्लोरोफॉर्म
(vi) पेन्टेनॉल
उत्तर:
जल, एक ध्रुवीय विलायक है जिसमें अणुओं के मध्य हाइड्रोजन बन्ध पाया जाता है।
(a) (ii) टॉलूईन तथा (v) क्लोरोफॉर्म जल में अविलेय हैं क्योंकि ये. सहसंयोजी यौगिक हैं, अतः ये जल के साथ हाइड्रोजन बन्ध नहीं बनाते।

(b) (i) फीनॉल तथा (vi) पेन्टेनॉल जल में आंशिक रूप से विलेय हैं क्योंकि इन यौगिकों में ध्रुवता होती है लेकिन इनका अध्रुवीय भाग बड़ा है। अतः ये जल के साथ बहुत दुर्बल हाइड्रोजन बन्ध बनाते हैं।

(c) (iii) फार्मिक अम्ल तथा (iv) एथिलीन ग्लाइकॉल जल में अत्यधिक विलेय हैं क्योंकि ये जल के साथ प्रबल हाइड्रोजन बन्ध बनाते हैं।

प्रश्न 2.26.
यदि किसी झील के जल का घनत्व 1.25 g mL^-1 है तथा उसमें 92 g Na⁺ आयन प्रति किलोग्राम जल में उपस्थित हैं, तो झील में Na⁺ आयन की मोललता ज्ञात कीजिए ।
उत्तर:

= \(\frac { 92 }{ 23 }\) = 4
अतः m = \(\frac { 4 }{ 1 }\) = 4
अतः Na⁺ आयन की मोललता = 4 m.

प्रश्न 2.27.
अगर CuS का विलेयता गुणनफल 6 × 10^-16 है तो जलीय विलयन में उसकी अधिकतम मोलरता ज्ञात कीजिए।
उत्तर:
CuS का विलेयता गुणनफल (k_sp) = [Cu2+][s2-] Cus की अधिकतम मोलरता = CuS की विलेयता
CuS का k_sp = 6 × 10^-16
तथा इसके लिए (K_sp) = S²
S = mol L^-1 में विलेयता

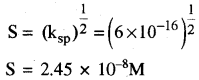
अतः जलीय विलयन में CuS की अधिकतम विलेयता = 2.45 × 10^-8 M

प्रश्न 2.28.
जब 6.5g, ऐस्पिरीन (C₉H₈O₄) को 450 g ऐसिटोनाइट्राइल (CH₃CN) में घोला जाए तो ऐस्पिरीन का ऐसीटोनाइट्राल में भार प्रतिशत (द्रव्यमान प्रतिशत) ज्ञात कीजिए ।
उत्तर:
भार प्रतिशत = × 100
अवयव (ऐस्पिरीन) का भार = 6.5 g
विलायक का भार = 450 g
विलयन का कुल भार = 450 + 6.5 g = 456.5 g
अतः ऐस्पिरीन का भार % = \(\frac { 6.5 }{ 456.5 }\) × 100 = 1.4238 = 1.424%

प्रश्न 2.29.
नैलॉफ़न (C₁₉H₂₁NO₃) जो कि मॉर्फीन जैसी होती है, का उपयोग स्वापक उपभोक्ताओं (narcotic users) द्वारा स्वापक छोड़ने से उत्पन्न लक्षणों को दूर करने में किया जाता है। सामान्यतया नैलॉफ़न की 1.5 mg खुराक दी जाती है। उपर्युक्त खुराक के लिए 1.5 × 10^-3 m जलीय विलयन का कितना द्रव्यमान आवश्यक होगा?
उत्तर:
मोललता (m)

विलेय का भार = 1.5 mg =1.5 × 10^-3(g)
विलेय (C₁₉H₂₁NO₃) का मोलर द्रव्यमान
=(12×19)+(1×21) +14+ (3×16) =228 +21+14 + 48 =311
m = 1.5 × 10^-3, विलायक का द्रव्यमान = ?
मान रखने पर,

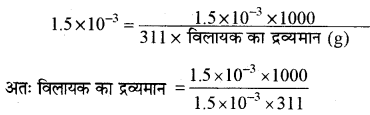
विलायक का द्रव्यमान = 3.215 g
विलयन का द्रव्यमान = 3.215(g) + 1.5 × 10^-3 (g)
= 3.215 + 0.0015
= 3.2165 = 3.217(g)

प्रश्न 2.30.
बेन्जोइक अम्ल का मेथेनॉल में 250 mL, 0.15 M विलयन बनाने के लिए आवश्यक मात्रा की गणना कीजिए।
उत्तर:
मोलरता (M) =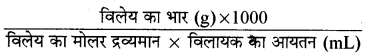
विलेय का द्रव्यमान = ?
विलेय [बेन्जोइक अम्ल (C₆H₅COOH)] का मोलर द्रव्यमान
=(6 × 12) + 5 + 12 + 16 + 16 + 1 = 122
M = 0.15
अतः 1.15 =
विलेय का द्रव्यमान = \(\frac{0.15 \times 250 \times 122}{1000}\)
विलेय का द्रव्यमान = 4.575 g

प्रश्न 2.31.
ऐसीटिक अम्ल, ट्राइक्लोरोऐसीटिक अम्ल एवं ट्राइफ्लुओरो ऐसीटिक अम्ल की समान मात्रा से जल के हिमांक में अवनमन इनके उपर्युक्त दिए गए क्रम में बढ़ता है। संक्षेप में समझाइए |
उत्तर:
हिमांक अवनमन कणसंख्यक अणुसंख्यक गुण है अर्थात् कणों की संख्या बढ़ने पर हिमांक अवनमन भी बढ़ेगा।

ऐसीटिक अम्ल (CH₃COOH), ट्राइक्लो रो ऐसीटिक अम्ल (CCl₃COOH) एवं ट्राइफ्लुओरो ऐसीटिक अम्ल (CF₃COOH) का यह क्रम अम्लीय गुण का बढ़ता क्रम है अर्थात् वियोजन का भी बढ़ता क्रम है अतः कणों की संख्या बढ़ेगी। इसलिए उपर्युक्त क्रम ही हिमांक में अवनमन का बढ़ता क्रम है।

प्रश्न 2.32.
CH₃ – CH₂ – CHCl – COOH के 10g को 250 g जल में मिलाने से होने वाले हिमांक का अवनमन परिकलित कीजिए। ( K_a = 1.4 × 10^-3, K_f = 1.86K kg mol^-1 तथा विलयन का घनत्व = 0.904g mL^-1 )
उत्तर:
विलयन की मोलरता

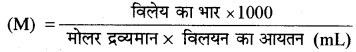
विलयन का द्रव्यमान = 250 + 10 = 260 g

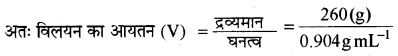
(V) = 287.6 mL
CH₃ – CH₂ – CHCl – COOH (C₄H₇O₂Cl) का मोलर
द्रव्यमान = 36 +7 32 + 35.5 = 122.5
∴ M = \(\frac{10 \times 1000}{122.5 \times 287.6 \mathrm{~mL}}\)
M = 0.2838 = 0.284mol L^-1
वान्ट हॉफ गुणांक (i) ज्ञात करना-

प्रश्न 2.33.
CH₂FCOOH के 19.5 g को 500g H₂O में घोलने पर जल के हिमांक में 1.0°C का अवनमन देखा गया। फ्लुओरोऐसीटिक अम्ल का वान्ट हॉफ गुणक तथा वियोजन स्थिरांक परिकलित कीजिए, यदि K_f = 1.86 K kg mol^-1 तथा विलयन का घनत्व = 1.124 g mL^-1 ।
उत्तर:
(i) विलयन की मोललता =
विलेय का भार = 19.5g
CH₂FCOOH का मोलर द्रव्यमान = 12 + 2 + 19 + 12 + 16 + 16 + 1 = 78
विलायक का द्रव्यमान = 500 g
अतः m = \(\frac{19.5 \times 1000}{78 \times 500}\) = 0.5
हिमांक अवनमन △T_f = 1.0°

(ii) △T_f = i × K_f × m

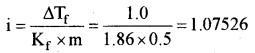
वान्ट हॉफ गुणक (i) = 1.0753

(iii) अम्ल की वियोजन की मात्रा α = \(\frac{i-1}{n-1}\)
α = \(\frac{1.0753 – 1}{2 – 1}\) = 0.0753

(iv) वियोजन की मात्रा (α) = \(\sqrt{\frac{\mathrm{K}_{\mathrm{a}}}{\mathrm{C}}}\)

प्रश्न 2.34.
293 K पर जल का वाष्प दाब 17.535 mm Hg है। यदि 25 g ग्लूकोस को 450 g जल में घोलें तो 293 K पर जल का वाष्प दाब परिकलित कीजिए।
उत्तर:
जल का वाष्प दाब p₁⁰ = 17.535mm Hg
माना विलयन का वाष्प दाब = P₁
वाष्प दाब में आपेक्षिक अवनमन = \(\frac{p_1^0-p_1}{p_1^0}\) = x₂
n₁ = विलायक (जल) के मोल = \(\frac{450}{18}\)
ग्लूकोस (C₆H₁₂O₆) का मोलर द्रव्यमान = 180
n₂ = विलेय के मोल = \(\frac{25}{180}\)

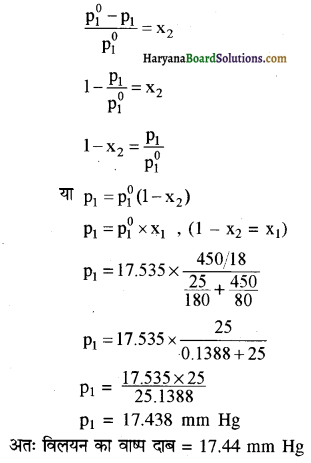
प्रश्न 2.35.
298K पर मेथेन की बेन्जीन में मोललता का हेनरी स्थिरांक 4.27 × 10⁵ mm Hg है । 298K तथा 760 mm Hg दाब पर मेथेन की बेन्जीन में विलेयता परिकलित कीजिए।
उत्तर:
दिया हुआ है K_H = 4.27 × 10⁵ mm Hg,
p = 760mm Hg
हेनरी के नियम के अनुसार p = K^H.x
मेथेन की मोल भिन्न (x) = \(\frac{\mathrm{p}}{\mathrm{K}_{\mathrm{H}}}\)
x = \(\frac{760}{4.27 \times 10^5}\)
x = 177.9 × 10^-5
x = 178 × 10^-5
अतः मेथेन की बेन्जीन में विलेयता (मोल भिन्न के रूप में) = 178 × 10^-5

प्रश्न 2.36.
100g द्रव A (मोलर द्रव्यमान 140 gmol^-1) को 1000 g द्रव B ( मोलर द्रव्यमान 180gmol- 1 ) में घोला गया। शुद्ध द्रव B का वाष्प दाब 500 Torr पाया गया। शुद्ध द्रव A का वाष्प दाब तथा विलयन में उसका वाष्प दाब परिकलित कीजिए यदि विलयन का कुल वाष्प दाब 475 Torr हो ।
उत्तर:
माना द्रव A का शुद्ध अवस्था में वाष्प दाब = P_A⁰ तथा शुद्ध
अवस्था में द्रव B का वाष्प दाब P_B⁰ = 500 Torr
द्रव A के मोल
(n_A) = = \(\frac { 100 }{ 140 }\) = 0.714
द्रव B के मोल
(n_B) = \(\frac { 1000 }{ 180 }\) = 5.55
द्रव A की मोल भिन्न
(x_A) = \(\frac{\mathrm{n}_{\mathrm{A}}}{\mathrm{n}_{\mathrm{A}}+\mathrm{n}_{\mathrm{B}}}\)
x_A = \(\frac{0.714}{0.714+5.55}\)
x_A = \(\frac { 0.714 }{ 6.264 }\) = 0.1139 = 0.114

द्रव B की मोल भिन्न
(X_B) = (1 − x_A) = (1 − 0.114) = 0.886
डाल्टन के आंशिक दाब के नियम से
कुल दाब (p) = P_A + P_B

प्रश्न 2.37.
328 K पर शुद्ध ऐसीटोन एवं क्लोरोफॉर्म के वाष्प दाब क्रमशः 741.8 mm Hg तथा 632.8 mm Hg हैं। यह मानते हुए कि संघटन के सम्पूर्ण परास में ये आदर्श विलयन बनाते Pकुल’ Pक्लोरोफॉर्म, तथा Pऐसीटोन को X ऐसीटोन के फलन के रूप में

उपर्युक्त आंकड़ों को भी उसी ग्राफ में आलेखित कीजिए और इंगित कीजिए कि क्या इसमें आदर्श विलयन से धनात्मक अथवा ऋणात्मक विचलन है?
उत्तर:
दिए गए आंकड़ों से कुल दाब ज्ञात करके विभिन्न आंकड़ों के लिए प्राप्त सारणी निम्न प्रकार है-

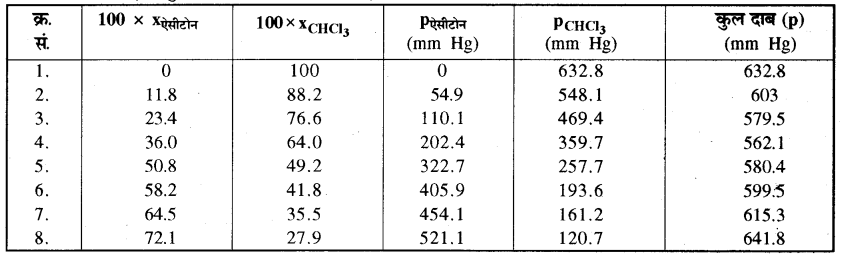
यहाँ कुल दाब (Pकुल) = Pऐसीटो + PCHCl₃
इन आंकड़ों से xऐसीटोन के फलन के रूप में (x अक्ष पर), Pकुल, Pक्लोरोफॉर्म तथा Pऐसीटोन (y अक्ष पर) को आलेखित करने पर प्राप्त ग्राफ निम्नलिखित प्रकार का होता है। (ग्राफ बनाते समय, दोनों अक्षों के लिए भिन्न-भिन्न पैमाना माना जाता है)-

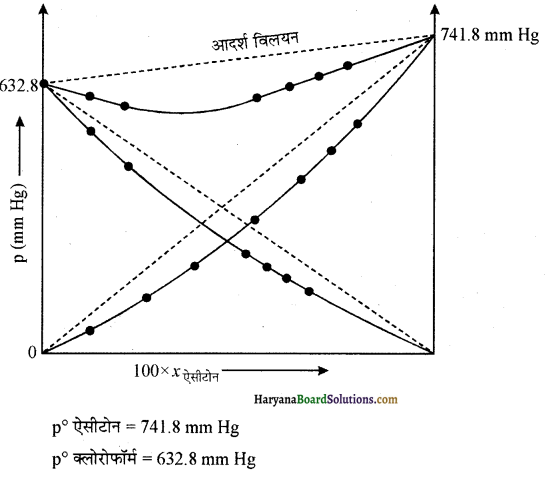
ग्राफ से यह ज्ञात होता है कि सभी संघटनों पर विलयन का कुल दाब, आदर्श विलयन के वाष्प दाब से कम है अतः इससे यह निष्कर्ष निकलता है कि विलयन ऋणात्मक विचलन दर्शाता है। जिसके लिए
ΔΗ_{मिश्रण} = -ve तथा △V_{मिश्रण} = -ve

प्रश्न 2.38.
संघटनों के सम्पूर्ण परास (Range) में बेन्जीन तथा टॉलूईन आदर्श विलयन बनाते हैं। 300 K पर शुद्ध बेन्जीन तथा टॉलूईन का वाष्प दाब क्रमश: 50.71 mm Hg तथा 32.06 mm Hg है। यदि 80g बेन्जीन को 100g टॉलूईन में मिलाया जाये तो वाष्प अवस्था में उपस्थित बेन्जीन के मोल-अंश परिकलित कीजिए ।
उत्तर:
माना वाष्प अवस्था में बेन्जीन का मोल अंश = Y₂ तो

टॉलूईन (C₇H₈) का मोलर द्रव्यमान = 92
अतः टॉलूईन के मोल (n₁) = \(\frac { 100 }{ 92 }\) = 1.086
विलयन में बेन्जीन का मोल अंश
x₂ = \(\frac{n_2}{n_1+n_2}\) = \(\frac{1.025}{1.086+1.025}\)
x₂ = \(\frac{1.025}{2.111}\) = 0.485
टॉलूईन का मोल अंश (x₁) = 1 – x₂
x1 = 1 – 0.485
x1 = 0.515
वाष्प अवस्था में बेन्जीन का मोल अंश

अतः वाष्प अवस्था में बेन्जीन का मोल अंश
(y₂) = 0.60
तथा वाष्प अवस्था में टॉलूईन का मोल अंश
(y₁) = 1 – y₂ = 1 – 0.60 = 0.40

प्रश्न 2.39.
वायु अनेक गैसों की मिश्रण है। 298 K पर आयतन में मुख्य घटक ऑक्सीजन और नाइट्रोजन लगभग 20% एवं 79% के अनुपात में हैं। 10 वायुमंडल दाब पर जल वायु के साथ साम्य में है। 298 K पर यदि ऑक्सीजन तथा नाइट्रोजन के हेनरी स्थिरांक क्रमश: 3.30 × 10⁷ mm तथा 6.51 × 10⁷ mm है, तो जल में इन गैसों का संघटन ज्ञात कीजिए ।
उत्तर:
माना 1 मोल वायु का 10 वायुमण्डल दाब ( atm P) पर आयतन = V
वायु में 20% O₂ (आयतन से) है,
अतः O₂ का आयतन = \(\frac{V \times 20}{100}\) = 0.2V
N₂ का वायु में प्रतिशत (आयतन से) = 79%
अतः N₂ का आयतन = \(\frac{\mathrm{V} \times 79}{100}\) = 0.79V
किसी गैस का आंशिक दाब = × कुल दाब
O₂ का आंशिक दाब, P_O2 = \(\frac{0.2 \mathrm{~V}}{\mathrm{~V}}\) × 10 = 2atm
N₂ का आंशिक दाब, P_N2 = \(\frac{0.79 \mathrm{~V}}{\mathrm{~V}}\) × 10 = 7.9atm
अतः विलयन में O₂ की विलेयता (मोल अंश के रूप में)
हेनरी के नियम से :

अतः जल में O₂ की विलेयता ( मोल भिन्न) = 4.606 × 10^-5
तथा N² की विलेयता (मोल भिन्न) = 9.22 × 10^-5

प्रश्न 2.40.
यदि जल का परासरण दाब 27° C पर 0.75 वायुमण्डल हो तो 2.5 लीटर जल में घुले CaCl₂ (i= 2.47 ) की मात्रा परिकलित कीजिए।
उत्तर:
परासरण दाब (Π) = iCRT
Π = 0.75atm. i = 2.47
C=?, R = 0.0821 L atm mol^-1 K^-1
T = 27°C = 27°C + 273.15 = 300.15K

विलेय के मोल = मोलरता (सान्द्रता ) × आयतन (L)
= 0.0123 × 2.5L = 0.030
अतः 2.5 लीटर जल में घुले CaCl₂ की मात्रा = 0.030 मोल

प्रश्न 2.41.
2 लीटर जल में 25°C पर K₂SO₄ के 25 mg, को घोलने पर बनने वाले विलयन का परासरण दाब, यह मानते हुए ज्ञात कीजिए कि K₂SO₄ पूर्णतः वियोजित हो गया है।
उत्तर:
K₂SO₄ का पूर्ण वियोजन माना गया है अतः

अतः आयनन से प्राप्त आयनों की संख्या (i) = 3
परासरण दाब (π) = iCRT
R = 0.0821 L atm mol^-1 K^-1

HBSE 12th Class Chemistry विलयन Intext Questions

प्रश्न 2.1.
यदि 22 g बेन्जीन 122g कार्बनटेट्राक्लोराइड में घुली हो तो बेन्जीन एवं कार्बन टेट्राक्लोराइड के द्रव्यमान प्रतिशत की गणना कीजिए।
उत्तर:
किसी अवयव का द्रव्यमान

विलयन में बेन्जीन का द्रव्यमान = 22 g
कार्बन टेट्राक्लोराइड का द्रव्यमान = 122 g
(i) अतः बेन्जीन का द्रव्यमान प्रतिशत = \(\frac { 22 }{ 122+22 }\) x 100
= \(\frac { 22 }{ 144 }\) × 100
= 15.277%
= 15.28%

(ii) कार्बनटेट्राक्लोराइड का द्रव्यमान प्रतिशत = \(\frac { 122 }{ 144 }\) x 100
= 84.72%
अतः बेन्जीन का द्रव्यमान %= 15.28% तथा कार्बनटेट्राक्लोराइड का द्रव्यमान % = 84.72% है।

प्रश्न 2.2.
एक विलयन में बेन्जीन का 30% द्रव्यमान कार्बन टेट्राक्लोराइड में घुला हुआ हो तो बेन्जीन के मोल- अंश की गणना कीजिए।
उत्तर:
विलयन में किसी अवयव का मोल अंश (Mole fraction) (x)

बेन्जीन का 30% द्रव्यमान कार्बन टेट्राक्लोराइड में घुला हुआ है। जिसका अर्थ है कि 30 g बेन्जीन (C₆H₆), 70g कार्बनटेट्राक्लोराइड (CC₁₄) में घुली हुई है।
किसी पदार्थ के मोलों की संख्या

(i) C₆H₆ का मोलर द्रव्यमान
= 78gmol^-1 (C = 12,H = 1)
CCl₄ का मोलर द्रव्यमान
= 154 g mol<sup<-1 (Cl = 35.5)
C₆H₆ के मोल (n_b = \(\frac { 30 }{ 78 }\) = 0.3846 mol
C₄H₄ के मोल (n_c = \(\frac { 70 }{ 154 }\) = 0.4545 mol
कुल मोल = n_b + n_c = 0.3846 + 0.4545 = 0.8391

(ii) बेन्जीन का मोल अंश (x_b) = \(\frac{n_b}{n_b+n_c}\)
x_b = \(\frac{0.3846}{0.8391}\) = 0.459
कार्बनटेट्राक्लोराइड का मोल अंश
(x_c) = \(\frac{0.4545}{0.8391}\)
= 0.54165
= 0.541
अतः C₆H₆ का मोल अंश = 0.459
CCl₄ का मोल अंश = 0.541

प्रश्न 2.3.
निम्नलिखित प्रत्येक विलयन की मोलरता की गणना कीजिए-
(क) 30 g, Co (NO₃)₂.6H₂O 4.3 लीटर विलयन में घुला हुआ हो
(ख) 30mL 0.5M H₂SO₄ को 500 ml तक तनु करने पर।
उत्तर:
(क) किसी विलयन की मोलरता

Co(NO₃)₂.6H₂O का द्रव्यमान 30 g
तथा इसका मोलर द्रव्यमान = 297 g mol^-1 होता है।
अतः Co(NO₃)₂.6H₂O के मोल = \(\frac{30 \mathrm{~g}}{297 \mathrm{~g} \mathrm{~mol}^{-1}}\)
विलयन का आयतन = 4.3 लीटर
अतः Co(NO₃)₂.6H₂O की मोलरत
(M) = \(\frac{30 \mathrm{~g}}{297 \mathrm{~g} \mathrm{~mol}^{-1} \times 4.3 \mathrm{~L}}\)
M = 0.02349 = 0.0235 = 0.024
अतः विलयन की मोलरता = 0.024 M.

(ख) किसी विलयन को तनु करने पर उसकी परिणामी मोलरता निम्नलिखित सूत्र से ज्ञात कर सकते हैं-
M₁V₁ = M₂V₂
30ml 0.5 H₂SO को 500ml तक त किया गया है अतः
M₁ = 0.5. V₁ = 30ml, V₂ = 500mL, M₂ = ?
\(\frac{\mathrm{M}_1 \mathrm{~V}_1}{\mathrm{~V}_2}=\frac{0.5 \times 30}{500}\) = 0.03
अतः H₂SO₄ के विलयन की परिणामी मोलरता 0.03M

प्रश्न 2.4
यूरिया (NH₂CONH₂) के 0.25 मोलर, 2.5 kg जलीय विलयन को बनाने के लिए आवश्यक यूरिया के द्रव्यमान की गणना कीजिए।
उत्तर:
जल का घनत्व \(\simeq\) 1 g cm^-3
अतः 2.5 kg जलीय विलयन = 2500 g विलयन
= 2500 mL विलयन = 2.5 L विलयन
चूंकि विलयन अति है (0.25) अतः विलयन का घनत्व, जल के घनत्व के समान मान सकते हैं।

प्रश्न 2.5.
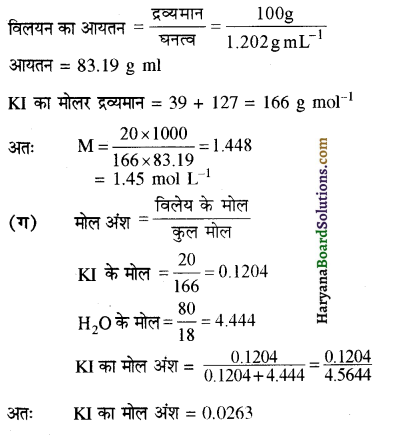
20% ( w / w ) जलीय KI का घनत्व 1202 gm^-1 हो तो KI विलयन की (क) मोललता, (ख) मोलरता, (ग) मोल अंश की गणना कीजिए।
उत्तर:
(क) विलयन की मोललता

20% w/w जलीय KI विलयन का अर्थ है कि 20 g KI, 80 g जल में विलेय है
KI का मोलर द्रव्यमान = 39 + 127 = 166

20% w/w जलीय KI विलयन का अर्थ है कि 20 g KI, 80 g जल में विलेय है

प्रश्न 2.6.
सड़े हुए अंडे जैसी गंध वाली विषैली गैस H₂ गुणात्मक विश्लेषण में उपयोग की जाती है। यदि H₂S गैस की जल में STP पर विलेयता 0.195 M हो तो हेनरी स्थिरांक की गणना कीजिए।
उत्तर:
हेनरी के नियमानुसार p = K_H.x
K_H = हेनरी स्थिरांक
p = दाब = 1bar (STP)
x = विलेय की मोल भिन्न
H₂S के मोल = 0.195M
तथा जल का मोल = 55.5 होता है।
अतः
x_H2s = \(\frac{0.195}{0.195+55.5}\)
= \(\frac{0.195}{55.695}\) = 0.0035 = 3.5 x 10^-3
हेनरी स्थिरांक K_H = \(\frac { P }{ x }\)
= \(\frac{1 \text { bar }}{3.5 \times 10^{-3}}\) = 285.7 bar
अतः H₂S के लिए हेनरी स्थिरांक (K_H) = 285.7 bar

प्रश्न 2.7.
298K पर CO₂ गैस की जल में विलेयता के लिए हेनरी स्थिरांक का मान 1.67 x 10⁸ Pa है। 500mL सोडा जल 2.5 atm दाब पर बंद किया गया। 298K ताप पर घुली हुई CO₂ की मात्रा की गणना कीजिए।
उत्तर:
हेनरी के नियम के अनुसार
X = \(\frac{\mathrm{p}}{\mathrm{K}_{\mathrm{H}}}\)
p = 2.5 atm, K_H = 1.67 × 10⁸ Pa
CO₂ की मोल भिन्न (x) = \(\frac{2.5 \mathrm{~atm}}{1.67 \times 10^8 \mathrm{~Pa}}\)
चूंकि 1 atm = 101325 Pa
अतः X_CO2 = \(\frac{2.5 \times 101325 \mathrm{~Pa}}{1.67 \times 10^8 \mathrm{~Pa}}\)
= 1.516 x 10^-3
X_CO2= 1.516 x 10^-3

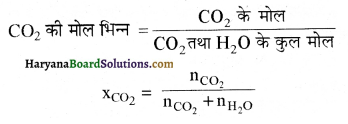
हेनरी का नियम अति तनु विलयन पर ही लागू होता है अतः n_CO2 << n_H2O
इस प्रकार
X_CO2 = \(\frac{\mathrm{n}_{\mathrm{CO}_2}}{\mathrm{n}_{\mathrm{H}_2 \mathrm{O}}}\)
चूंकि जल का मोल = 55.5 होता है
तथा X_CO2 = 1.516 × 10^-3
1.516 × 10^-3 = \(\frac{\mathrm{n}_{\mathrm{CO}_2}}{55.5}\)
n_CO2 = 1.516 x 10^-3 x 55.5
= 84.13 x 10^-3 L^-1
चूंकि विलयन का आयतन = 500mL
अतः CO₂ के 500mL विलयन (0.5L) में उपस्थित मोल = \(\frac{84.13 \times 10^{-3}}{2}\)
= 42.06 x 10^-3
CO₂ का द्रव्यमान = मोल x मोलर द्रव्यमान
CO₂ का मोलर द्रव्यमान 12 + (2 x 16) = 44
अतः CO₂ का द्रव्यमान = 42.06 x 10^-3 x 44
CO₂ का द्रव्यमान = 1.85 g

प्रश्न 2.8.
350 K पर शुद्ध द्रवों A एवं B के वाष्पदाब क्रमश: 450 एवं 750mm Hg हैं। यदि कुल वाष्पदाब 600 mm Hg हो तो द्रव मिश्रण का संघटन ज्ञात कीजिए। साथ ही वाष्प प्रावस्था का संघटन भी ज्ञात कीजिए।
उत्तर:
मिश्रण का कुल वाष्प दाब = P_कुल = P_A + P_B
P_A = x_AP°_A, P_B = x_BP°_B
अतः P_कुल = x_AP°_A + x_BP°_B
P_कुल = 600mm Hg, p°_A = 450mm Hg
तथा p°_B = 750 mm Hg.
अतः P_कुल= 450x_A + 700x_B (x_B =1 – x_A)
600 = 450x_A + 700 (1 – x_A)
600 = 450x_A + 700 – 700x_A
200x_A= 100
x_A = \(\frac { 100 }{ 250 }\) = 0.4
x_A + x_B = 1
अतः x_B = 1 – 0.4 = 0.6
अतः द्रव मिश्रण का संघटन = x_A = 0.4, x_B = 0.6
वाष्प अवस्था में
P_A = y_APकुल
y_A = \(\frac{\mathrm{p}_{\mathrm{A}}}{\mathrm{y}_{\text {कुल }}}=\frac{\mathrm{x}_{\mathrm{A}} \mathrm{p}_{\mathrm{A}}^{\mathrm{o}}}{\mathrm{p}_{\text {कुल }}}=\frac{450 \times 0.4}{600}\)
y_A = 0.3
y_B = 1 – y_A = 1 – 0.3 = 0.7
अतः वाष्प अवस्था में मिश्रण का संघटन
= Y_A = 0.3, y_B = 0.7

प्रश्न 2.9.
298 K पर शुद्ध जल का वाष्पदाब 23.8 mm H है। 850g जल में 50g यूरिया (NH₂CONH₂) घोला जाता है। इस विलयन के लिए जल के वाष्पदाब एवं इसके आपेक्षिक अवनमन का परिकलन कीजिए।
उत्तर:
वाष्प दाब में आपेक्षिक अवनमन विलेय की मोल अंश के बराबर होता है।
\(\frac{\mathrm{p}_1^0-\mathrm{p}_1}{\mathrm{p}_1^0}=\frac{\mathrm{n}_2}{\mathrm{n}_1+\mathrm{n}_2}\)
n₂ = विलेय के मोल
= \(\frac { 50g }{ 60 }\)(यूरिया का मोलर द्रव्यमान = 60)
n₁ = विलायक के मोल = \(\frac { 850 g }{ 18 }\)

शुद्ध जल का वाष्प दाब p°1 = 23.8mm Hg
अतः p₁ = 23.8 x 0.983 = 23.39mm Hg
अतः
इस विलयन के लिए जल का वाष्प दाब
= 23.39 mm Hg
= 23.4 mm Hg
तथा वाष्प दाब का आपेक्षिक अवनमन = 0.017

प्रश्न 2.10
750 mm Hg दाब पर जल का क्वथनांक 99.63°C है। 500 g जल में कितना सुक्रोस मिलाया जाए कि इसका 100° C पर क्वथन हो जाए।
उत्तर:
क्वथनांक उन्नयन ∆T_b = 100 – 99.63 = 0.37°
क्वथनांक उन्नयन ∆T_b = \(\frac{\mathrm{K}_{\mathrm{b}} \times 1000 \times \mathrm{w}_2}{\mathrm{M}_2 \times \mathrm{w}_1}\)
K_b = क्वथनांक उन्नयन स्थिरांक ( मोलल उन्नयन स्थिरांक)
= 0.52 kg mol^-1
M₂ = विलेय का मोलर द्रव्यमान = 342 (सुक्रोस) C₁₂H₂₂O₁₁
w₂ = विलेय का भार = ?
w₁ = विलायक का भार = 5000 g
∆T_b = 0.37 = \(\frac{0.52 \times 1000 \times \mathrm{w}_2}{342 \times 500}\)
w₂ = \(\frac{0.37 \times 342 \times 500}{0.52 \times 1000}\)
w₂ = 121.67 g
अतः 121.67g सुक्रोस मिलाना पड़ेगा।

प्रश्न 2.11.
ऐस्कार्बिक अम्ल (विटामिन C, C₆H₈O₆) के उस द्रव्यमान का परिकलन कीजिए, जिसे 75g ऐसीटिक अम्ल में घोलने पर उसके हिमांक में 1.5°C की कमी हो जाए। K_f = 3.9 K kg mol^-1
उत्तर:
हिमांक अवनमन, ∆T_f = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{w}_2 \times 100}{\mathrm{M}_2 \times \mathrm{w}_1}\)
∆T_f = 1.5°C, K_f = 3.9 K kg mol^-1 w₂ = ?
w₁ = 75g, M₂ = 176 (C₆H₈O₆)
1.5 = \(\frac{3.9 \times w_2 \times 1000}{176 \times 75}\)
w₂ = \(\frac{1.5 \times 176 \times 75}{3.9 \times 1000}\)
w₂ = 5.0769 g
अतः ऐस्कॉर्बिक अम्ल का द्रव्यमान 5.077g

प्रश्न 2.12.
185,000 मोलर द्रव्यमान वाले एक बहुलक के 1.0 g को 37°C पर 450 mL जल में घोलने से उत्पन्न विलयन के परासरण दाब का पास्कल में परिकलन कीजिए।
उत्तर:
परासरण दाब II = CRT
II = \(\frac{\mathbf{n}_2}{\mathrm{~V}}\)RT
II = परासरण दाब
n₂ = पदार्थ के मोल = 1.0 g/185000
R = 0.083 L bar mol^-1K^-1
T = 37°C + 273.15 = 310.15
V = 450mL = 0.45L
परासरण दाब (II) = \(\frac{1.0 \times 0.083 \times 310.15}{0.450 \times 185,000}\) = 3.09 x 10^-4
= 3.09 × 10^-4 x 101325 Pa
= 31.309 Pa