HBSE 10th Class Science Notes Chapter 10 Light Reflection and Refraction

Haryana State Board HBSE 10th Class Science Notes Chapter 10 Light Reflection and Refraction Notes.

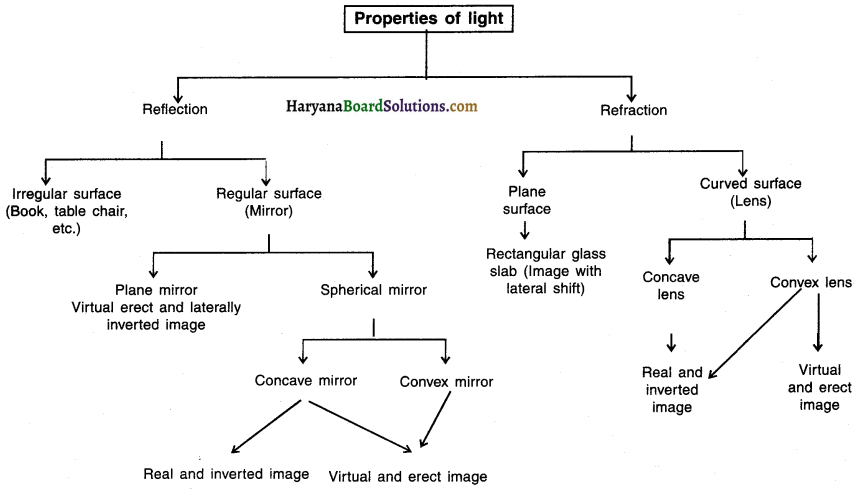
Haryana Board 10th Class Science Notes Chapter 10 Light Reflection and Refraction

Light:

• When light falls on an object let us say a book, or a table, etc., it gets reflected, The reflected light rays reach our eyes and enable us to see the object.
• Light waves do not require a material medium (like solid, liquid or gas) for their propagation and hence are called non-mechanical waves.
• When light is incident on a surface separating two medias such as air and water, then some part of incident light is reflected, some part is transmitted and some part of it is absorbed by that surface.

Reflection of Light

Reflection :

The phenomenon of sending back the light rays which fall on the surface of an object when light is incident on it, is called reflection of light.

Types:

• Regular reflection and
• Irregular (diffused) reflection

Image:

When a number of rays emerging from a point of an object, after reflection or refraction, ‘meet’ or ‘appear to meet’ at another point, then the point of meeting is called the image of the first point.

Types:

• Real image and
• Virtual image

Real Image: When the rays of light after reflection or refraction ‘actually meet’ at a point, the image formed is called a real image.

Virtual Image: When the rays of light after reflection or refraction ‘do not actually meet’ but ‘appear to meet’ at a point, the image formed is called a virtual image.

A polished/shining surface which reflects almost all the light incident on it is called a mirror.

Types of mirror:

(1) Plane mirror and (2) Spherical mirror.
Further, spherical mirrors are of two types. They are: (a) Concave mirror and (b) Convex mirror.

Spherical Mirrors

Plane mirror :
A plane mirror is a thin, flat and smooth sheet of glass having a shining coat of silver metal on one side. For example, mirror used in vehicles,in dressing tables, etc.

Spherical mirror :
Unlike plane mirrors, spherical (curved) mirrors converge or diverge the parallel light rays incident on them.

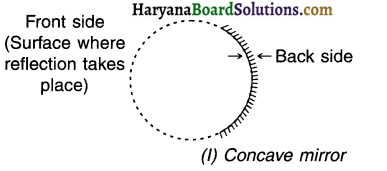
Concave mirror:
The spherical mirror in which light rays converge to form an image is called a concave mirror (or converging mirror).

Convex mirror:
A spherical mirror in which light rays diverge to form an image is called a convex mirror (or diverging mirror).

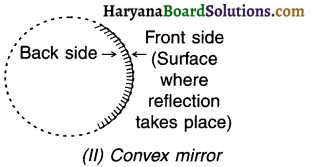
Image Formation by Spherical Mirrors and Representation of Images Formed by Spherical Mirrors Using Ray Diagrams

• The image of an object formed by a spherical mirror (or a lens) can be obtained and studied by constructing a ray diagram.
• Two rays are sufficient to draw a ray diagram because by intersecting two reflected rays we can obtain the position of the image formed.

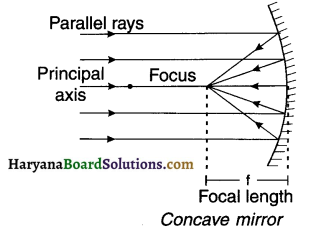
Converging (Concave) mirror:

When parallel rays are incident on concave mirror,on reflection, they converge i.e. come closer to each other and meet at a point called principal focus (F). Hence, concave mirror is also called a converging mirror.

Diverging (Convex) mirror:

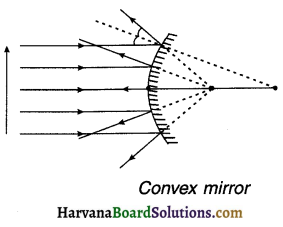
When parallel rays are incident on convex mirror, on reflection, they diverge i.e. spread out from each other. Hence, convex mirror is also called a diverging mirror.

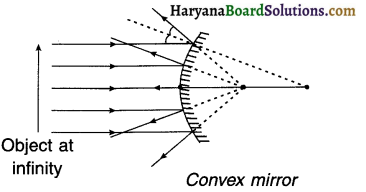
Relation between radius of curvature (R) and focal length (f) of a spherical mirror:

Focal length\((f)=\frac{1}{2} R=\frac{R}{2}\)
Obtaining Images through concave., and convex mirrors

Positions at which we can place an object to obtain images from a concave mirror and summary of the images formed:

Summary of images formed in a concave mirror

Position of object	Position of Image	Size of image	Nature of Image
1. At infinity 2. Beyond C(i.e. 2F) 3. On C (i.e. on 2F) 4. Between F and C 5. On principal focus F 6. Between P and F	At F Between F and C On C Beyond C At infinity Behind the mirror	Highly diminished Diminisified Same as object size Enlarged Highly enlarged Enlarged	Real and inverted Real and inverted Real and inverted Real and inverted Real and inverted Virtual and erect

Positions at which we can place an object to obtain Images from a convex mirror and summary of the images formed:

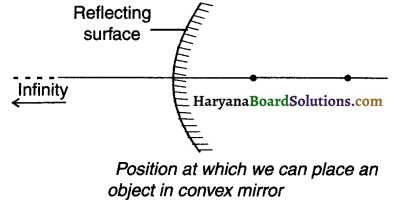
Summary of images formed in a convex mirror

Position of object	Position of image	Size of image	Nature of image
1. At infinity 2. Anywhere between infinity and pole P of the mirror	At focus F, behind the mirror Between pole P and focus F, behind the mirror	Highly diminished Diminished	Virtual and erect Virtual and erect

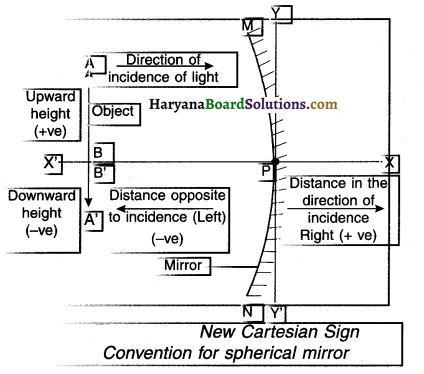
Sign Convention for Reflection by Spherical Mirrors

Summary of New Cartesian Sign Convention for reflection by spherical mirror:

Mirror Formula and Magnification :

• The relationship between the object distance (u), image distance (v) and focal length (f) of a mirror is called the mirror formula.
  As per mirror formula:\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
• The ratio of image height (h’) to object height (h) is called the magnification (m).
  Thus, for spherical mirrors, magnification \((m)=\frac{\text { Height of image }\left(h^{\prime}\right)}{\text { Height of object }(h)} \quad \text { i.e. } m=\frac{h^{\prime}}{h}\)
•  In terms of object distance (u) and image distance (y), magnification (m) can be expressed as, \(m=\frac{h^{\prime}}{h}=-\frac{v}{u}\)

Summary of size of image, type of image and magnification for various mirrors

Refraction of Light

Refraction:
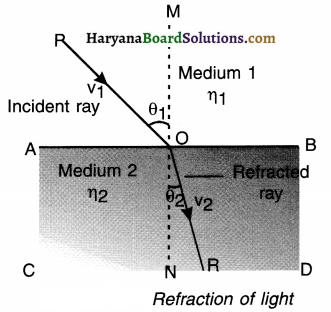
When a ray of light enters obliquely from one transparent medium to another transparent medium, its velocity changes due to which it gets deviated from its original direction at the surface separating two medias. This is called refraction.

Medium:
A transparent substance in which light can travel is called a medium. Air, water, gas, glass, kerosene, etc. are examples of mediums.

• Optically rarer medium: A medium in which the speed of light is more is called optically rarer medium. For example, air.
• Optically denser medium: A medium in which the speed of light is less (compared to optically rarer medium) is called an optically denser medium. For example glass and water (in comparison to air).

Relative Refractive index :

• The ratio of speed of light v₁ in medium 1 to the speed of light v₂ in medium 2 is known as the relative refractive index of medium 2 with respect to medium 1 (except the medium of vacuum).
• It is denoted by η₂₁ i.e. refractive index of medium 2 with respect to medium 1.

∴ Refractive index \(\eta_{21}=\frac{\text { Speed of light in medium } 1}{\text { Speed of light in medium } 2}=\frac{v_1}{v_2}\)

Moreover, Absolute refractive index \(\eta_{\mathrm{m}}=\frac{\text { Speed of light in vacuum }}{\text { Speed of light in medium }}=\frac{\mathrm{c}}{\mathrm{v}}\)

Snell’s law:
The ratio of sine of angle of incidence to the ratio of sine of angle of refraction is constant.
∴ \(\eta_{21}=\frac{\sin \theta_1}{\sin \theta_2}\)

Refraction by Spherical Lenses and Formation of Images

Lens: A lens is a piece of transparent glass bound by two spherical surfaces.

Types: Convex (Converging) lens:
A lens which is thick at the center and tapered at the upper and lower ends is called a convex lens.

Concave (Diverging) lens:
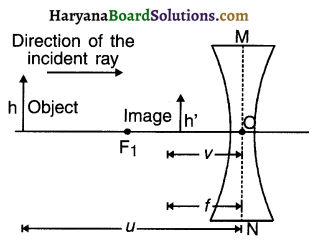
A lens which is thin in the middle but thicker at the edges is called concave lens.

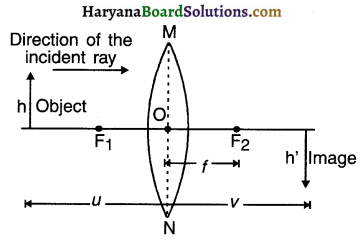
Positions at Which we can place an object in front of convex lens and the summary of images formed:

Summary of images formed by convex lens

No.	Position of the object	Position of the image	Size of image	Nature of image
1	At infinite distance	On opposite side of lens at F2	Highly diminished	Real & inverted
2	Beyond 2F1	On opposite side of lens between F2 & 2F2	Diminished	Real & inverted
3	At 2F1	On opposite side of lens at 2F2	Same as object	Real & inverted
4	Anywhere between F1 & 2F1	On opposite side of lens beyond 2F2	Enlarged	Real & inverted
5	At F1	At infinity	Highly enlarged	Real & inverted
6	Anywhere between O & F1	On the same side of the lens as the object beyond 2F1	Enlarged	Virtual & erect

Summary of images formed by concave lens

No.	Position of the Object	Position of the Image	Size of Image	Nature of Image
1.	At infinity	On the same side of a lens as the object at focus F1	Highly diminished	Virtual & erect
2.	Between O & infinity	On the same side as object between O & focus F1	Diminished lens as the object	Virtual & erect

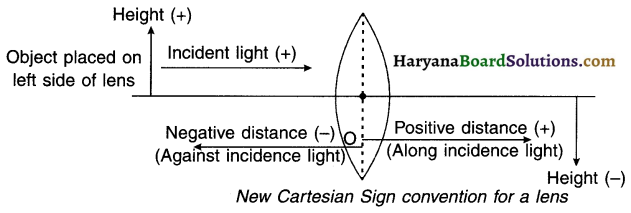
Summary of New Cartesian Sign Convention followed for refraction of light through spherical lenses

Power of Lens

The power of lens (P) is the “Reciprocal of the focal length (f) of lens”.
∴ Power of lens (P) = \(\frac{1}{f}\)