HBSE 10th Class Maths Important Questions Chapter 3 Pair of Linear Equations in Two Variables

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 3 Pair of Linear Equations in Two Variables Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 3 Pair of Linear Equations in Two Variables

Short/Long Answer Type Questions

Question 1.
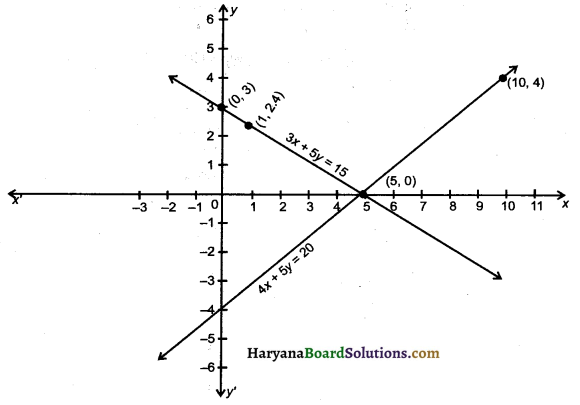
Solve the following pair of linear equation by graphical method : 4x – 5y = 20, and 3x + 5y = 15, with the help of this find the value of m while 4x + 3y = m.
Solution :
The given equations are:
4x – 5y = 20 …………(1)
And 3x + 5y = 15 …………..(2)
For representation of these equations graphically, we draw the graphs of these equations as follows:
4x – 5y = 20
y = \(\frac{20-4 x}{-5}\)
y = \(\frac{4 x-20}{5}\)
We put the different values of x in this equation, then we get different values of y and we prepare the table of x, y for the equaiton 4x – 5y = 20.

x	5	10	– 1
y	0	4	– 4.8

And 3x + 5y = 15
⇒ y = \(\frac{15-3 x}{5}\)
We put the different values of x in this equation, then we get different values of y and we prepare the table of x, y for the equation 3x + 5y = 15.

x	0	5	1
y	3	0	2.4

Now, we plot the values of x hind y from tables 1 and 2 on the graph paper and we draw the graphs of the equations 1 and 2, those passes through these values.
Observe that we get two straight lines which intersect each other at point (5, 0). Hence, x = 5, y = 0 is the required solution put these values of x and y in the equation 4x + 3y = m, we get
4 × 5 + 3 × 0 = m
⇒ 20 + 0 = m
⇒ m = 20

Question 2.
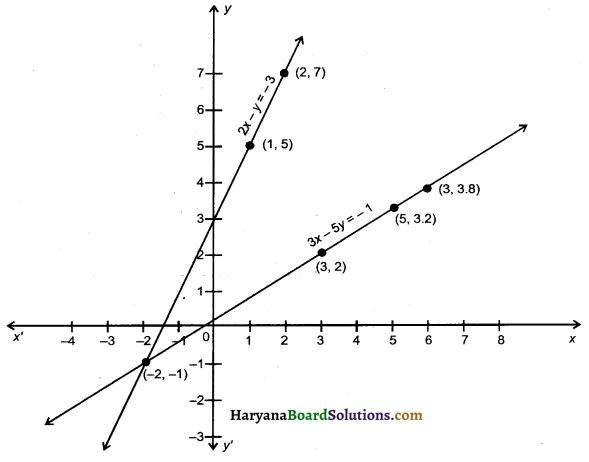
Solve the following pair of linear equations by graphical method :
3x – 5y = – 1 and 2x – y = – 3. Thus find the value of A in the relation (x + y)² = A
Solution :
The given equation are :
3x – 5y = – 1
And 2x – y = – 3 …………(2)
For representation of these equations graphically, we draw the graphs of these equations are follows:
3x – 5y = – 1
⇒ y = \(\frac{-1-3 x}{-5}\)
⇒ y = \(\frac{3 x+1}{5}\)
We put the different values of x in this equation, then we get different values of y and we prepare the table of x and y for the equation 3x – 5y = – 1.

x	3	5	6
y	2	3.2	3.8

And 2x – y = – 3
y = \(\frac{-3-2 x}{-1}\)
= 3 + 2x
We put the different values of x in this equation, then we get different values of y and we prepare the table of x and y for the equation
2x – y = – 3

x	1	2	– 2
y	5	7	– 1

Now, we plot the values of x and y from tables 1 and 2 on the graph paper and we draws the graphs of equations 1 and 2 those passes through these values.

Observe that we get two straight lines which intersects each other at point (-2, -1) Hence, x = -2, y = -1 is the required solution put the values of x and y in the equation (x + y)² = A, we get
[- 2 + (-1)]² = A
(-3) = A
A = 9

Question 4.
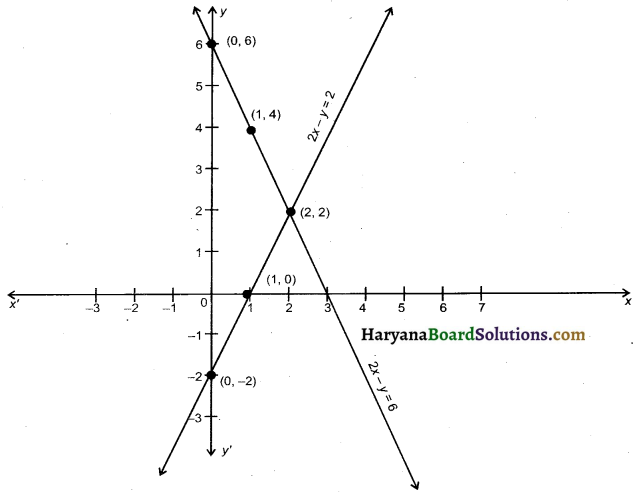
Solve the following pair of linear equations by graphical method 2x + y = 6 and 2x – y = 2. Thus find the value of P in the relation 6x + 7y = P.
Solution :
The given equations are :
2x + y = 6 ………..(1)
And 2x – y = 2 …………(2)
For representation of these equations graphically, we draw the graphs of these equations as follows
2x + y = 6
⇒ y = 6 – 2x
We put the different values of x in this equation, then we get different galues of y and we prepare the table of x, y for the equation 2x + y = 6.

x	1	2	0
y	4	2	6

And 2x – y = 2
⇒ y = \(\frac{2-2 x}{-1}\)
⇒ y = 2x – 2
We put the different values of x in this equation, then we get different values of y and we prepare the table of x and y for the equation
2x – y = 2

x	0	1	2
y	– 2	0	2

Now, we plot the values of x and y from tables 1 and 2 on the graph paper and we draw the graphs of the equations 1 and 2, those passes through these values.
Observe that we get two different straight lines which intersect each other at point (2, 2).
Hence, x = 2, y = 2 is the required solution. Put the values of x and y in the relation
6x + 7y = P we get
6 × 2 + 7 × 2 = P
⇒ 12 + 14 = P
⇒ P = 26

Question 5.
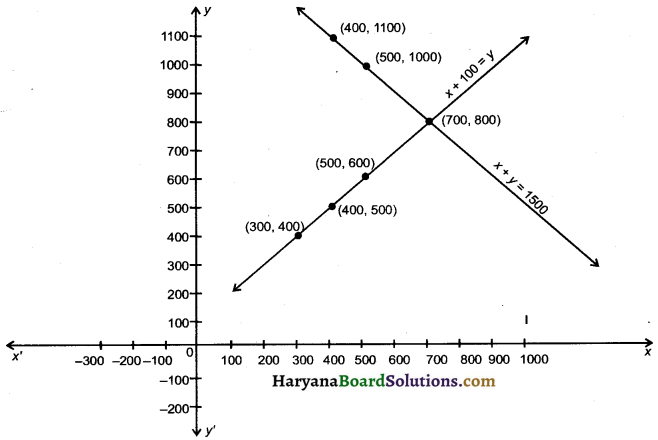
For ultarakhand Flood victims two reactions A and B of class 10 contributed ₹ 1500. If the contribution of class 10, A was ₹ 100 less than that of class 10 B, find the graphically the amount contributed by both reactions.
Solution :
Let contribution of A be ₹ x and contribution of B be ₹ y.
According to question
x + y = 1500 ………….. (1)
Contribution of A is ₹ 100 less than that of B
∴ x + 100 = y ………… (2)
For representation of these equations graphically, we draw the graphs of these equations as follows:
x + y = 1500
⇒ y = 1500 – x
We put the different values of x in this equation, then we get different values of y and we prepare the table of x, y for the equation
x + y = 1500

x	400	500	700
y	1100	1000	800

And x + 100 = y
⇒ y = x + 100
We put the different values of x in this equation, then we get different value of y and we prepare the table of x, y for the equation
x + 100 = y

x	400	500	300
y	500	600	400

Now, we plot the values of x and y from tables 1 and 2 on the graph paper and we draw the graphs of the equations 1 and 2 those passes through these values.
Observe that we get two different straight lines which intersect each other at point (700, 800)
Hence,
x = ₹ 700,
y = ₹ 800
Therefore, contribution of A is ₹ 700 and contribution of B is ₹ 800.

Question 6.
If 2x + y = 23 and 4x – y = 19, find the value of (5y – 2x) and (\(\frac {y}{x}\)– 2)
Solution :
The given equations are :
2x + y = 23 ………(1)
4x – y = 19 ……..(2)
Adding equation (1) and (2) we get
6x = 42
⇒ x = \(\frac {42}{6}\) = 7
Substituting the value of x in equation (1), we get
2 × 7 + y = 23
⇒ y = 23 – 14 = 9
So, x = 7, y = 9
Putting the values of x and y in 5y – 2x, we get 5 × 9 – 2 × 7 = 45 – 14 = 31.
And putting the values of x and y in the \(\frac {y}{x}\) – 2, we get
\(\frac {9}{7}\) – 2 = \(\frac{9-14}{7}=\frac{-5}{7}\)
Hence, 5y – 2x = 31 and \(\frac {y}{x}\) – 2 = – \(\frac {5}{7}\)

Question 7.
A father’s age is three times the sum of the ages of his two children. After 5 years his age will be two times the sum of their ages. Find the present age of the father.
Solution :
Let the age of father be x years and the sum of ages of his children be y years.
According to questions,
x = 3y …….. (1)
After 5 years
Age of father = (x + 5) years
And sum of ages of his children = (y + 10) years
According to the question,
x + 5 = 2(y + 10)
⇒ x + 5 = 2y + 20
⇒ x – 2y = 20 – 5
⇒ x – 2y = 15 ……..(2)
From equation (1), substituting the value of x in the equation, we get
3y – 2y – 15
⇒ y = 15 years
Putting the value of y in the equation we get
x = 3 × 15 = 45 years
Hence, present age of father = 45 years.

Question 8.
Raghav scored 70 marks in a test, getting 4 marks for each right answer and losing 1 mark for each wrong answer. Had 5 marks been awarded for each correct answer and 2 marks been deducted for each wrong answer, then Raghav would have scored so marks. How many questions were there in the test.
Solution :
Let the number of right answers be x and number of wrong answers be y.
According to question,
4x – y = 70 ………… (1)
And 5x – 2y = 80 ………..(2)
Multiplying equation in (1) by 2 and substracting equ. (2) from equ. (1), we get

⇒ x = \(\frac {60}{3}\) = 20
Substituting the value of x in the equ. (1) we
4 × 20 – y = 70
⇒ – y = 70 – 80 = – 10
⇒ y = 10.
Hence, total number of questions = x + y = 20 + 10 = 30.

Question 9.
In a painting competition of a school a child made Indian national flag whose perimeter was 50 cm. Ita area will be decreased by 6 square em, if length is decreased by 3 cm and breadth is increased by 2 cm then find the dimension of flag.
Solution :
Let the length of the flag be x cm and its breadth be y cm,
so, its area = xy cm² ………..(1)
According to condition (i)
2(x + y) = 50
⇒ x + y = 25 …….(2)
If length is decreased by 3 cm. then new length is (x – 3) cm. And breadth is increased by 2 cm then new breadth is (y + 2) cm.
New area = (x – 3) (y + 2) cm²
According to condition (ii)
(x – 3) (y + 2) = xy – 6 [Using equ. (1)]
⇒ xy + 2x – 3y – 6 = xy – 6
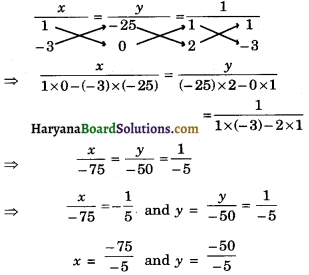
⇒ 2x – 3y = 0 ……(3)
So, the equation of pair is
x + y – 25 = 0 …….(2)
2x – 3y + 0 = 0 …….(3)
By cross multiplication method, we get

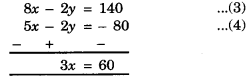
⇒ x = 15 cm and y = 10 cm.
Hence, length of flag is 15 cm and its breadth is 10 cm.

Question 10.
Sumit is 3 times as old as his son. Five years later, he shall be two and half times as old as his son. How old is sumit at present age ?
Solution :
Let present age of sumit be x years and present age of his son be y years.
According to question
x = 3y
x – 3y = 0 …….. (1)
After 5 years later
Age of sumit = (x + 5) years
And age of his son = (y + 5) years
According to question,
x + 5 = 2\(\frac {1}{2}\)(y + 5)
x + 5 = \(\frac {5}{2}\)(y + 5)
2x + 10 – 5y + 25
2x – 5y = 25 – 10
2x – 5y = 15
Multiplying equation (1) by 2 and substracting eqn. (2) from equ. (1), we get

⇒ y = 15
y = 15 Substituting the value of y in the equ. (1) we
x – 3 × 15 = 0
⇒ x = 45 years
Hence, present age of sumit = 45 years.

Question 11.
For what value of k, will the following pair of equations have infinitely many solutions :
2x + 3y = 7 and (k + 2) x – 3 (1 – k)y = 5k + 1.
Solution :
The given equations are :
2x + 3y – 7 = 0
And (k + 2)x – 3 (1 – k)y – (5k + 1) = 0
The condition for infinitely many solutions is :
⇒ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
⇒ \(\frac{2}{k+2}=\frac{3}{-3(1-k)}=\frac{-7}{-(5 k+1)}\)
⇒ – 6 (1 – k) = 3k + 6
and – 10k – 2 = – 7k – 14
⇒ – 6 + 6k = 3k + 6
and – 10k + 7k = – 14 + 2
⇒ 3k = 12 and – 3k = – 12
⇒ k = 4 and k = \(\frac {-12}{-3}\) = 4
Hence k = 4

Question 12.
For what values of m and n the following system of linear equations has infinitely many solutions:
3x + 4y = 12 and (m + n)x + 2 (m -n)y = 5m – 1.
Solution :
The given equations are :
3x + 4y – 12 = 0 ………(1)
(m + n)x + 2(m – n)y – (5m – 1) = 0
The condition for infinitely many solution is :

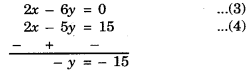
⇒ 6m – 6n = 4m + 4n
and 15m – 3 = 12m + 12n
⇒ 6m – 4m = 6n + 4n
and 15m – 12m – 12n = 3
2m = 10n and 3m – 12n = 3
⇒ m = 5n and m – 4n = 1
Putting the value of m in (m – 4n = 1) we get
5n – 4n = 1
n = 1
Putting the value of n is m = 5n, we get
m = 5 × 1 = 5
Hence, m = 5, n = 1.

Fill in the Blanks

Question 1.
If \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) the pair of equations a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 is …………
Solution :
Inconsistent

Question 2.
The graph of a pair of linear equations in two variables is represented by two ……………. lines.
Solution :
Straight

Question 3.
Every solution of a linear equation in two variables is a ………. on the line representing it.
Solution :
Point

Question 4.
A pair of linear equation in two variables can be represented and solved by the algebraic and ………….. methods.
Solution :
Graphical

Question 5.
If the lines are ……….. then the pair of linear equations in two variables has no solution.
Solution :
Parallel

Question 6.
The general form of a pair of ……………… equations in two variables x and y is a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 where \(a_1^2+b_1^2\) ≠ 0, \(a_2^2+b_2^2\) ≠ 0.
Solution :
Linear.

Multiple Choice Questions

Question 1.
The value of k for which the system of linear equations x + 2y = 3, 5x + ky + 7 = 0 is inconsistent is :
(a) – \(\frac {14}{3}\)
(b) \(\frac {2}{5}\)
(c) 5
(d) 10
Solution :
(d) 10

Given equation are :
x + 2y – 3 = 0 And
5x + ky + 7 = 0
The condition for inconsistant is:
\(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Taking first two order, we get
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)
⇒ \(\frac{1}{5}=\frac{2}{k}\)
⇒ k = 10

Question 2.
The value of k for which the system of equations.
2x + 3y = 5
4x + ky = 10 has infinite number of solutions, is :
(a) 3
(b) 6
(c) 0
(d) 1
Solution :
(b) 6

For inifinite number of solutions
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
\(\frac{2}{4}=\frac{3}{k}=\frac{5}{10}\)
⇒ k = \(\frac {12}{2}\) = 6
So correct option (b).

Question 3.
The value of k for which the given system of equations has a unique solution is :
kx + 2y – 5 = 0
x + 3y – 2 = 0
(a) ≠ \(\frac {3}{2}\)
(b) ≠ \(\frac {2}{3}\)
(c) ≠ \(\frac {2}{3}\)
(d) ≠ \(\frac {3}{2}\)
Solution :
(b) ≠ \(\frac {2}{3}\)

kx + 2y – 5 = 0
x + 3y – 2 = 0
For unique solution
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{k}{1} \neq \frac{2}{3}\)
⇒ k ≠ \(\frac {2}{3}\)
So correct option (b).

Question 4.
The value of k for which the system of equations
2x + 4y = 5
6x + ky = 9 has no solution, is :
(a) 10
(b) 9
(c) 12
(d) 11.
Solution :
(c) 12

2x + 4y = 5
6x + ky = 9
For no solution
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)
⇒ \(\frac{2}{6}=\frac{4}{k}\)
⇒ k = \(\frac{6 \times 4}{2}\) = 12
So correct option (c).

Question 5.
The values of a and b for which the following system of equations
2x – 3y = 7
(a + b)x – (a + b – 3)y = 4a + b has infinitely many solutions, are :
(a) a = -5, b = 2
(b) a = -2, b = -5
(c) a = -5, b = -1
(d) a = -1, b = -5.
Solution :
(c) a = -5, b = -1

2x – 3y = 7
(a + b)x – (a + b – 3)y
= 4a + b
For inifinitily many solutions 2 -3
\(\frac{2}{a+b}=\frac{-3}{-(a+b-3)}=\frac{7}{4 a+b}\)
By solving a = -5, b = – 1 so correct choice is (c).

Question 6.
For which values of P, will the lines represented by the following pair of linear equations be parallel 3x – y – 5 = 0, 6x – 2y – P = 0.
(a) all real values expect 10
(b) 10
(c) \(\frac {5}{2}\)
(d) \(\frac {1}{2}\)
Solution :
(a) all real values expect 10

The given equation are :
3x – y – 5 = 0 …………….(1)
6x – 2y – P = 0 …………….(2)
The condition for parallel lines is

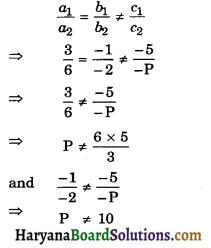
So, P can have any real values other than 10.