Haryana State Board HBSE 9th Class Maths Solutions Chapter 7 Triangles Ex 7.1 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 7 Triangles Exercise 7.1
Question 1.
In quadrilateral ACBD, AC = AD and AB bisects ∠A (see figure 7.26). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?
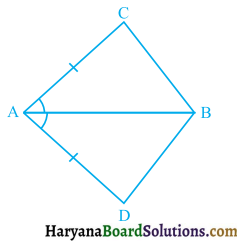
Solution :
In ΔABC and ΔABD, we have
AC = AD, (Given)
∠CAB = ∠DAB, (AB bisects ∠A)
and AB = AB, (Common)
∴ ΔABC ≅ ΔABD,
(By SAS congruence rule)
⇒ BC = BD, (CPCT)
Hence, BC and BD are equal
![]()
Question 2.
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see figure 7.27).
Prove that:
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
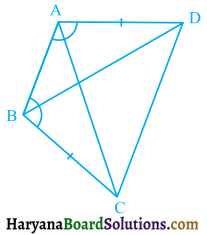
Solution :
(i) In ΔABD and ΔBAC,
we have AD = BC, (Given)
∠DAB = ∠CBA, (Given)
and AB = AB, (Common)
ΔABD ≅ ΔBAC (By SAS congruence rule)
Hence proved
(ii) ∵ ΔABD ≅ ΔBAC,
(As proved above)
⇒ BD = AC, (CPCT)
Hence proved
(iii) ∵ ΔABD ≅ ΔBAC
(As proved above)
⇒ ∠ABD = ∠BAC, (CPCT)
Hence proved
Question 3.
AD and BC are equal perpendiculars to a line segment AB (see figure 7.28). Show that CD bisects AB.
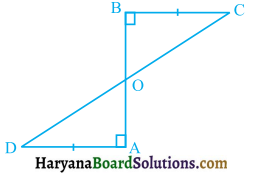
Solution:
In ΔAOD and ΔBOC, we have
∠OAD = ∠OBC, (Each = 90°)
∠AOD = ∠BOC,
(Vertically opposite angles)
and AD = BC, (Given)
∴ ΔAOD ≅ ΔBOC,
(By AAS congruence rule)
⇒ OA = OB, (CPCT) or CD bisects AB. Hence proved
![]()
Question 4.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see figure 7.29). Show that ΔABC ≅ ΔCDA.
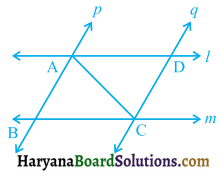
Solution:
Since two parallel lines l and m intersected by another pair of parallel lines p and q.
Therefore AD || BC and AB || DC
∴ AD || BC and AC is the transversal.
∠ACB = ∠DAC (A pair of alternate interior angles)
Again, AB || DC and AC is the transversal.
∠BAC = ∠ACD, (A pair of alternate interior angles)
Now in ΔABC and ΔCDA, we have Fig. 7.28
∠ACB = ∠DAC,
(As proved above)
AC = AC (common)
and ∠BAC = ∠ACD,
(As proved above)
∴ ΔABC ≅ ΔCDA [By ASA congruence rule]
Hence proved
Question 5.
Line l is the bisector of an angle A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see figure 7.30). Show that:
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A
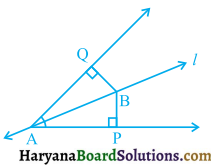
Solution:
(i) In ΔAPB and ΔAQB, we have
∠APB = ∠AQB, (Each = 90°)
∠PAB = ∠QAB,
(Line l bisects ZA) and
AB = AB, (Common)
∴ ΔAPB ≅ ΔAQB, (By AAS congruence rule)
Hence proved
(ii) ∵ ΔAPB ≅ ΔAQB,
(As proved above)
⇒ BP = BQ (CPCT)
or B is equidistant from the arms of ∠A.
Hence proved
![]()
Question 6.
In figure 7.31, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
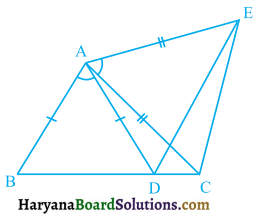
Solution:
We have
∠BAD = ∠EAC (Given)
⇒ ∠BAD + ∠CAD = ∠EAC + ∠CAD,
(Adding ∠CAD on both sides)
⇒ ∠BAC = ∠DAE ……….(i)
Now in ΔABC and ΔADE, we have
AB = AD (Given)
∠BAC = ∠DAE,
(As proved above)
and AC = AE (Given)
∴ ΔABC ≅ ΔADE,
(By SAS congruence rule)
⇒ BC = DE (CPCT)
Hence proved
Question 7.
AB is a line segment and Pis its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure 7.32). Show that:
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE
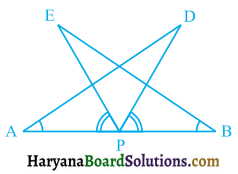
Solution:
(i) We have
∠EPA = ∠DPB (Given)
⇒ ∠EPA + ∠EPD = ∠DPB + ∠EPD.
(Adding ∠EPD on both sides)
⇒ ∠APD = ∠BPE ………….(i)
Now, ΔDAP and ΔEBP, we have
∠BAD = ∠ABE (Given)
⇒ ∠DAP = ∠EBP,
AP = PB,
(P is the midpoint of AB)
and ∠APD = ∠BPE,
(As proved above (i))
∴ ΔDAP ≅ ΔEBP (By ASA congruence rule)
Hence proved
(ii) ∵ ΔDAP ≅ ΔEBP,
(As proved above)
⇒ AD = BE (CPCT)
Hence proved
![]()
Question 8.
In right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure 7.33). Show that:
(i) ΔAMC ≅ ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC ≅ ΔACB
(iv) CM = \(\frac {1}{2}\)AB.
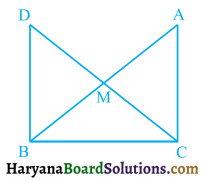
Solution :
(i) In ΔBMD and ΔAMC, we have
BM = AM
(M is the mid point of AB)
DM = CM, (Given)
∠BMD = ∠AMC,
(Vertically opposite angles)
∴ ΔBMD ≅ ΔAMC (By SAS congruence rule)
Hence proved
(ii) ΔBMD ≅ ΔAMC, [As proved above in solution (i)]
⇒ BD = AC, …(1) (CPCT)
and ∠DBM = ∠CAM (CPCT)
But these are alternate interior angles.
DB || AC, [By theorem 6.3]
Now DB || AC and BC is the transversal.
∠DBC + ∠ACB = 180°, (A pair of allied angles are supplementary)
⇒ ∠DBC + 90° = 180°
∵ ∠ACB = 90° (Given)
⇒ ∠DBC = 180° – 90°
⇒ ∠DBC = 90°
⇒ So, ∠DBC is a right angle. Hence proved
(iii) In ΔDBC and ΔACB, we have
DB = AC, (From (i)]
∠DBC = ∠ACB, [Each = 90°] and
BC = BC, (common)
ΔDBC ≅ ΔACB, (By SAS congruence rule)
Hence proved
(iv) ΔDBC ≅ ACB [As proved above in solution (iii)] (CPCT)
⇒ DC = AB,
⇒ \(\frac {1}{2}\)DC = \(\frac {1}{2}\)AB (Multiply by 1/2 on both sides)
⇒ CM = \(\frac {1}{2}\)AB [∵ M is the mid point of DC and AB respectively)
Hence proved