HBSE 9th Class Maths Solutions Chapter 15 प्रायिकता Ex 15.1

Haryana State Board HBSE 9th Class Maths Solutions Chapter 15 प्रायिकता Ex 15.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 15 प्रायिकता Exercise 15.1

प्रश्न 1.
एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेदों में 6 बार चौका मारती है। चौका न मारे जाने की प्रायिकता ज्ञात कीजिए।
हल :
यहां पर,
कल संभाव्य परिणामों की संख्या = 30
कुल अनुकूल परिणामों की संख्या = 6
इसलिए चौका मारने की प्रायिकता = P (E) = \(\frac{6}{30}\) = \(\frac{1}{5}\)
P(चौका न मारा जाना) = 1 – \(\frac{1}{5}\)
= \(\frac{5-1}{5}=\frac{4}{5}\) उत्तर

प्रश्न 2.
2 बच्चों वाले 1500 परिवारों का यदृच्छया चयन किया गया है और निम्नलिखित आंकड़े लिख लिए गए हैं :

परिवार में लड़कियों की संख्या	2	1	0
परिवारों की संख्या	475	814	211

यदृच्छया चुने गए उस परिवार की प्रायिकता ज्ञात कीजिए, जिसमें
(i) दो लड़कियां हों
(ii) एक लड़की हो
(iii) कोई लड़की न हो
साथ ही, यह भी जांच कीजिए कि इन प्रायिकताओं का योगफल 1 है या नहीं।
हल :
(i) यहां पर,
कुल संभाव्य परिणामों (कुल परिवारों) की संख्या = 475 + 814 + 211 = 1500
दो लड़कियों वाले परिवारों (अनुकूल परिणामों) की संख्या = 475
P (दो लड़कियों वाले परिवार) = \(\frac{475}{1500}=\frac{19}{60}\) उत्तर

(ii) यहां पर,
कुल संभाव्य परिणामों (कुल परिवारों) की संख्या = 475 + 814 + 211 = 1500
1 लड़की वाले परिवारों (अनुकूल परिणामों) की संख्या = 814
P (एक लड़की वाले परिवार) = \(\frac{814}{1500}=\frac{407}{750}\) उत्तर

(iii) यहां पर,
कुल संभाव्य परिणामों (कुल परिवारों) की संख्या = 475 + 814 + 211 = 1500
0 लड़की वाले परिवारों (अनुकूल परिणामों) की संख्या = 211
P (कोई लड़की न हो) = \(\frac{211}{1500}\) उत्तर

प्रश्न 3.
अध्याय 14 के अनुच्छेद 14.4 का उदाहरण 5 लीजिए। कक्षा के किसी एक विद्यार्थी का जन्म अगस्त में होने की प्रायिकता ज्ञात कीजिए।
हल :
प्रश्नानुसार,
वर्ष में जन्में कुल विद्यार्थी (संभाव्य परिणामों की संख्या) = 40
अगस्त मास में जन्में विद्यार्थी (अनुकूल परिणामों की संख्या) = 6
∴ P (अगस्त में जन्म लेने वाला विद्यार्थी) = \(\frac{6}{40}=\frac{3}{20}\) उत्तर

प्रश्न 4.
तीन सिक्कों को एक साथ 200 बार उछाला गया है तथा इनमें विभिन्न परिणामों की बारंबारताएं ये हैं :

परिणाम	3 चित	2 चित	1 चित	कोई भी चित नहीं
बारंबारता	23	72	77	28

यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित के आने की प्रायिकता ज्ञात कीजिए। [B.S.E.H. March, 2017, 2020]
हल :
यहां पर,
कुल संभाव्य परिणामों की संख्या = 200 (23 + 72 + 77 + 28)
दो चित आने के अनुकूल परिणामों की संख्या = 72
∴ P (दो चित आएं) = \(\frac{72}{200}=\frac{9}{25}\) उत्तर

प्रश्न 5.
एक कंपनी ने यदृच्छया 2400 परिवार चुनकर एक घर की आय स्तर और वाहनों की संख्या के बीच संबंध स्थापित करने के लिए उनका सर्वेक्षण किया। एकत्रित किए गए आंकड़े नीचे सारणी में दिए गए हैं :

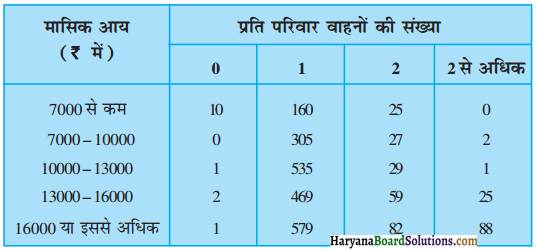
मान लीजिए एक परिवार चुना गया है। प्रायिकता ज्ञात कीजिए कि चुने गए परिवार
(i) की आय ₹ 10000 – 13000 प्रति माह है और उसके पास ठीक-ठीक दो वाहन हैं।
(ii) की आय प्रति माह ₹ 16000 या इससे अधिक है और उसके पास ठीक 1 वाहन है।
(iii) की आय ₹ 7000 प्रति माह से कम है और उसके पास कोई वाहन नहीं है।
(iv) की आय ₹ 13000 – 16000 प्रति माह है और उसके पास 2 से अधिक वाहन हैं।
(v) जिसके पास 1 से अधिक वाहन नहीं है।
हल :
कुल संभाव्य परिणामों की संख्या = 2400
(i) ₹ 10000 – 13000 प्रति माह कमाने वाले परिवारों में 2 वाहनों वाले परिवारों (अनुकूल परिणामों) की संख्या = 29
∴ P (₹ 10000 – 13000 प्रति माह कमाने वाले 2 वाहनों वाले परिवार) = \(\frac{29}{2400}\) उत्तर

(ii) ₹ 16000 या इससे अधिक प्रति माह कमाने वाले परिवारों में 1 वाहन वाले परिवारों (अनुकूल परिणामों) की संख्या = 579
∴ P (₹ 16000 या इससे अधिक प्रतिमाह कमाने वाले 1 वाहन वाले परिवार) = \(\frac{579}{2400}\) उत्तर

(iii) ₹ 7000 प्रति माह से कम कमाने वाले परिवारों में कोई वाहन न होने वाले परिवारों (अनुकूल परिणाम) की संख्या = 10
∴ P (₹ 7000 प्रति माह से कम कमाने वाले शून्य वाहन वाले परिवार) = \(\frac{10}{2400}=\frac{1}{240}\)

(iv) ₹ 13000 – 16000 प्रति माह कमाने वाले परिवारों में 2 से अधिक वाहनों वाले परिवारों (अनुकूल परिणाम) की संख्या = 25
∴ P(₹ 13000 – 16000 प्रति माह कमाने वाले 2 से अधिक वाहन वाले परिवार) = \(\frac{25}{2400}=\frac{1}{96}\)

(v) 1 से अधिक वाहन न रखने वाले परिवारों की संख्या
(अनुकूल परिणाम) = 10 + 0 + 1 + 2 + 1 + 160 + 305 + 535 + 469 + 579 = 2062
∴ P (1 से अधिक वाहन न रखने वाले परिवार) = \(\frac{2062}{2400}=\frac{1031}{1200}\) उत्तर

प्रश्न 6.
अध्याय 14 की सारणी 14.7 लीजिए।
(i) गणित की परीक्षा में एक विद्यार्थी द्वारा 20 से कम अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
(ii) एक विद्यार्थी द्वारा 60 या इससे अधिक अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।

अंक	विद्यार्थियों की संख्या
0-20	7
20-30	10
30-40	10
40-50	20
50-60	20
60-70	15
70 – और इससे अधिक	8
कुल योग	90

हल :
(i) यहां पर,
कुल विद्यार्थियों की संख्या (संभाव्य परिणाम) = 90
20 से कम अंक प्राप्त करने वाले विद्यार्थी (अनुकूल परिणाम) = 7
∴ P (20 से कम अंक प्राप्त करने वाले विद्यार्थी) = \(\frac{7}{90}\) उत्तर

(ii) 60 या उससे अधिक अंक प्राप्त करने वाले विद्यार्थी
(अनुकूल परिणाम) = 15 + 8 = 23
∴ P (60 या उससे अधिक अंक प्राप्त करने वाले विद्यार्थी) = \(\frac{23}{90}\) उत्तर

प्रश्न 7.
सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आंकड़ों को नीचे दी गई सारणी में लिख लिया गया है : [B.S.E.H. March, 2019]

मत	विद्यार्थियों की संख्या
पसंद करते हैं	135
पसंद नहीं करते हैं	65

प्रायिकता ज्ञात कीजिए कि यदृच्छया चुना गया विद्यार्थी
(i) सांख्यिकी पसंद करता है
(ii) सांख्यिकी पसंद नहीं करता है।
हल :
यहां पर,
कुल विद्यार्थियों की संख्या (संभाव्य परिणाम) = 135 + 65 = 200
(i) सांख्यिकी पसंद करने वाले विद्यार्थी (अनुकूल परिणाम) = 135
∴ P (सांख्यिकी पसंद करने वाले विद्यार्थी) = \(\frac{135}{200}=\frac{27}{40}\) उत्तर

(ii) सांख्यिकी पसंद न करने वाले विद्यार्थी (अनुकूल परिणाम) = 65
∴ P (सांख्यिकी पसंद न करने वाले विद्यार्थी) = \(\frac{65}{200}=\frac{13}{40}\)

प्रश्न 8.
प्रश्नावली 14.2 का प्रश्न 2 देखिए। इसकी आनुभविक प्रायिकता क्या होगी कि इंजीनियर :
(i) अपने कार्यस्थल से 7 कि०मी० से कम दूरी पर रहते हैं?
(ii) अपने कार्यस्थल से 7 कि०मी० या इससे अधिक दूरी पर रहते हैं?
(iii) अपने कार्यस्थल से \(\frac{1}{2}\) कि०मी० या इससे कम दूरी पर रहते हैं?
हल :
कल इंजीनियरों की संख्या (संभाव्य परिणाम) = 40
(i) अपने कार्यस्थल से 7 कि०मी० से कम दूरी पर रहने वाले इंजीनियरों की संख्या = 9
∴ P (एक इंजीनियर अपने कार्यस्थल से 7 कि०मी० से कम दूरी पर रहता है) = \(\frac{9}{40}\) उत्तर

(ii)
अपने कार्यस्थल से 7 कि०मी० या इससे अधिक दूरी पर रहने वाले इंजीनियरों की संख्या = 31
∴ P (एक इंजीनियर 7 कि०मी० या इससे अधिक दूरी पर रहता है) = \(\frac{31}{40}\) उत्तर

(iii) अपने कार्यस्थल से \(\frac{1}{2}\) कि०मी० या इससे कम दूरी पर रहने वाले इंजीनियरों की संख्या = 0
∴ P (एक इंजीनियर अपने कार्यस्थल से \(\frac{1}{2}\) कि०मी० या इससे कम दूरी पर रहता है) = \(\frac{0}{40}\) = 0 उत्तर

प्रश्न 9.
क्रियाकलाप : अपने विद्यालय के गेट के सामने से एक समय-अंतराल में गुजरने वाले दो पहिया, तीन पहिया और चार पहिया वाहनों की बारंबारता लिख लीजिए। आप के द्वारा देखे गए वाहनों में से किसी एक वाहन का दो पहिया वाहन होने की प्रायिकता ज्ञात कीजिए।
हल :
विद्यार्थी स्वयं हल करें।

प्रश्न 10.
क्रियाकलाप : आप अपनी कक्षा के विद्यार्थियों से एक 3 अंक वाली संख्या लिखने को कहिए। आप कक्षा से एक विद्यार्थी को यदृच्छया चुन लीजिए। इस बात की प्रायिकता क्या होगी कि उसके द्वारा लिखी गई संख्या 3 से भाज्य है? याद रखिए कि कोई संख्या 3 से भाज्य होती है, यदि उसके अंकों का योग 4 से भाज्य हो।
हल :
विद्यार्थी स्वयं हल करें।

प्रश्न 11.
आटे की उन ग्यारह थैलियों में, जिन पर 5 कि०ग्रा० अंकित है, वास्तव में आटे के निम्नलिखित भार (कि०ग्रा० में हैं:
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
यदृच्छया चुनी गई एक थैली में 5 कि०ग्रा० से अधिक आटा होने की प्रायिकता क्या होगी?
हल :
यहां पर,
आटे की कुल थैलियों की संख्या (संभाव्य परिणाम).= 11
5 कि०ग्रा० से अधिक भार वाली थैलियों की संख्या (अनुकूल परिणाम) = 7
P(5 कि०ग्रा० से अधिक भार वाली थैली) = \(\frac{7}{11}\) उत्तर

प्रश्न 12.
प्रश्नावली 14.2 के प्रश्न 5 में आपसे 30 दिनों तक एक नगर की प्रति वायु में सल्फर डाई-ऑक्साइड की भाग प्रति मिलियन में सांद्रता से संबंधित एक बारंबारता बंटन सारणी बनाने के लिए कहा गया था। इस सारणी की सहायता से इनमें से किसी एक दिन अंतराल (0.12-0.16) में सल्फर डाई-ऑक्साइड के सांदण होने की प्रायिकता ज्ञात कीजिए।

(ppm) में सल्फर डाई-ऑक्साइड का सांद्रण	बारंबारता
0.00-0.04	4
0.04-0.08	9
0.08-0.12	9
0.12-0.16	2
0.16-0.20	4
0.20-0.24	2
कुल योग	30

हल :
सारणी के अनुसार दिनों की कुल संख्या (संभाव्य परिणाम) = 30
जितने दिन (0.12 – 0.16) सांद्रता रही (अनुकूल परिणाम) = 2
∴ P (जितने दिन 0.12 – 0.16 सांद्रता रही) = \(\frac{2}{30}=\frac{1}{15}\) उत्तर

प्रश्न 13.
प्रश्नावली 14.2 के प्रश्न 1 में आपसे एक कक्षा के 30 विद्यार्थियों के रक्त-समूह से संबंधित बारंबारता बंटन सारणी बनाने के लिए कहा गया था। इस सारणी की सहायता से इस कक्षा से यदृच्छया चुने गए विद्यार्थी का रक्त-समूह AB होने की प्रायिकता ज्ञात कीजिए।

रक्त-समूह	विद्यार्थियों की संख्या
A	9
B	6
O	12
AB	3
कुल योग	30

हल :
सारणी के अनुसार विद्यार्थियों की कुल संख्या (संभाव्य परिणाम) = 30
AB रक्त-समूह वाले विद्यार्थियों की संख्या (अनुकूल परिणाम) = 3
∴ P (AB रक्त-संमूह वाला विद्यार्थी) = \(\frac{3}{30}=\frac{1}{10}\) उत्तर