Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 Circles Ex 10.6 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 10 Circles Exercise 10.6
[This exercise is not from examination point of view]
Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
Given: Two circles whose centres are O and O’ intersecting at A and B.
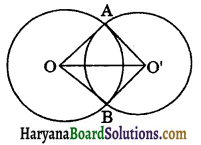
To prove : ∠OAO’ = ∠OBO’.
Proof: In ΔOAO’ and ΔOBO’, we have
OA = OB
[Equal radii of same circle]
O’A = O’B
[Equal radii of same circle]
OO’ = OO’ [Common]
ΔΟΑΟ’ = ΔΟΒΟ’
[By SSS congruence rule]
∠OAO’ = ∠OBO’ [CPCT]
Hence proved
![]()
Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution:
AB and CD are two parallel chords of a circle C(O, r). Draw OP ⊥ AB and OQ ⊥ CD.
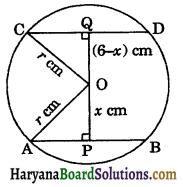
Let OP = x cm, then
OQ = 6 – x [∵ PQ = 6 cm]
Since, OP ⊥ AB
∴ AP = PB = \(\frac{1}{2}\)AB [By theorem 10.3]
⇒ AP = \(\frac{1}{2}\) × 5 [∵ AB = 5 cm]
⇒ AP = \(\frac{5}{2}\) cm
Again, OQ ⊥ CD
∴ CQ = QD = \(\frac{1}{2}\)CD [By theorem 10.3]
⇒ CQ = \(\frac{1}{2}\) × 11 [∵ CD = 11 cm]
⇒ CQ = \(\frac{11}{2}\) cm
In right ΔOPA, we have
AO2 = AP2 + OP2 [By Pythagoras theorem]
⇒ r2 = \(\left(\frac{5}{2}\right)^2+x^2\) …(i)
[∵ AP = \(\frac{5}{2}\) cm and OP = x cm]
In right ΔOQC, we have
OC2 = CQ2 + OQ2 [By Pythagoras theorem]
⇒ r2 = \(\left(\frac{11}{2}\right)^2\) + (6 – x)2
⇒ r2 = \(\frac{121}{4}\) + 36 + x2 – 12x …..(ii)
From (i) and (ii), we get
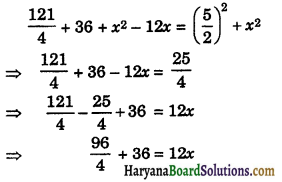
⇒ 24 + 36 = 12x
⇒ 60 = 12x
⇒ x = \(\frac{60}{12}\) = 5 cm
Putting the value of x in equation (i), we get

Hence, radius of the circle is \(\frac{5 \sqrt{5}}{2}\) cm.
Question 3.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre. what is the distance of the other chord from the centre?
Solution:
Let AB and CD be two parallel chords of the circle with centre O such that AB = 6 cm and CD = 8 cm.
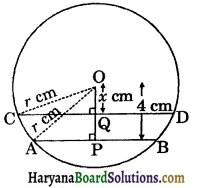
Let the radius of the circle be r сm.
draw OP ⊥ AB and OQ ⊥ CD.
Since, AB || CD, OP ⊥ AB and OQ ⊥ CD.
Therefore, O, Q and Pare collinear points.
OP = 4 cm
Let OQ = x cm
∵ OP ⊥ AB
∴ AP = PB = \(\frac{1}{2}\)AB
⇒ AP = \(\frac{1}{2}\) × 6
⇒ AP = 3 cm
Again, OQ ⊥ CD
∴ CQ = QD = \(\frac{1}{2}\)CD
⇒ CQ = \(\frac{1}{2}\) × 8
⇒ CQ = 4 cm
In right ΔOPA, we have
OA2 = AP2 + OP2 [By Pythagoras theorem]
⇒ r2 = 32 + 42 [∵ AP = 3 cm and OP = 4 cm]
⇒ r2 = 9 + 16
⇒ p2 = 25
⇒ r = \(\sqrt{25}\) = \(\sqrt{5 \times 5}\) = 5 cm
In right ΔOQC, we have
OC2 = CQ2 + OQ2 [By Pythagoras theorem]
⇒ r2 = 42 + x2 [∵ CQ = 4 cm and OQ = x cm]
⇒ 52 = 42 + x2
⇒ 52 – 42 = x2
⇒ (5 + 4) (5 – 4) = x2
⇒ 9 = x2
⇒ x = \(\sqrt{9}\) = \(\sqrt{3 \times 3}\) = 3 cm
Hence, distance of the other chord from the centre is 3 cm.
![]()
Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
In ΔBDC, we have
∠ADC = ∠DBC + ∠DCB …(i)
[∵ Exterior angle of a triangle is equal to sum of its opp. interior angles]
Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle.
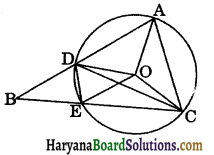
∴ ∠AOC = 2∠ADC
⇒ ∠ADC = \(\frac{1}{2}\)∠AOC … (ii)
Similarly, arc DE subtends ∠DOE at the centre and ∠DCE at the remaining part of the cricle.
∴ ∠DOE = 2∠DCE
⇒ ∠DOE = 2∠DCB
⇒ ∠DCB = \(\frac{1}{2}\)∠DOE …(ii)
From (ii) and (iii) the values of ∠ADC and ∠DCB put in (i), we get
\(\frac{1}{2}\)∠AOC = ∠DBC+ \(\frac{1}{2}\)∠DOE
∠DBC = \(\frac{1}{2}\)∠AOC – \(\frac{1}{2}\)∠DOE
∠ABC = \(\frac{1}{2}\)(∠AOC – ∠DOE)
[∵ ∠DBC = ∠ABC]
Hence, ∠ABC is equal to half the difference of angles subtended by the chords AC and DE at the centre.
Hence Proved
Question 5.
Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Solution:
Given: ABCD is a rhombus. A circle is drawn with AB as diameter. AC and BD are its diagonals.
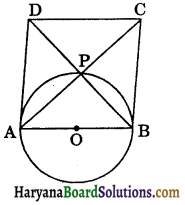
To prove: Circle passes through point P which is intersection of diagonals.
Proof: We know that the diagonals of a rhombus bisect each other at right angles.
∴ ∠APB = 90°.
But, angle in a semicircle is 90°. Thus, circle passes through P.
Hence, circle passes through point P which is the intersection of diagonals AC and BD of rhombus ABCD.
Proved
![]()
Question 6.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Solution:
Given: ABCD is a parallelogram. The circle passes through A, B, C and D (produced CD).
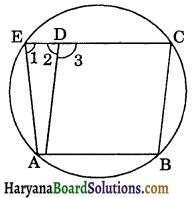
To prove: AE = AD.
Proof : Since, ABCD is a parallelogram.
∴ ∠ABC = ∠3 …..(i)
(Opposite angles of a || gm)
∵ ABCE is a cyclic quadrilateral.
∴ ∠ABC + ∠1 = 180° [Sum of opposite angles of a cyclic quadrilateral is 180°]
⇒ ∠3 + ∠1 = 180° [Using (i)] …(ii)
But, ∠2 + ∠3 = 180° (By linear pair axiom)…(ii)
From (ii) and (iii), we get
∠3 + ∠1 = ∠2 + ∠3
⇒ ∠1 = ∠2
⇒ AE = AD [Sides opposite to equal angles are equal]
Hence, AE = AD.
Proved
Question 7.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
Solution:
Given: AC and BD are chords of a circle, intersecting at O such that OA = OC and OB = OD.
To prove: (i) AC and BD are diameters of the circle.
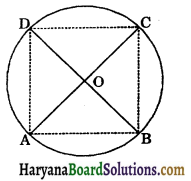
(ii) ABCD is a rectangle.
Construction: Join AB, BC, CD and AD.
Proof: (i) In ΔAOD and ΔCOB, we have
AO = OC (given)
OD = OB (given)
∠AOD = ∠COB (vertically opposite angles)
∴ ΔAOD ≅ ΔCOB (By SAS congruence rule)
⇒ AD = BC (CPCT)
⇒ \(\overparen{A D}=\overparen{B C}\) …..(i)
In ΔAOB and ΔCOD, we have
OA = OC (given)
OB = OD (given)
∠AOB = ∠COD (Vertically opposite angles)
∴ ΔАОВ ≅ ΔCOD (By SAS congruence rule)
⇒ AB = CD (CPCT)
⇒ \(\overparen{A B}=\overparen{C D}\) ……..(ii)
Adding (i) and (ii), we get
\(\widehat{A D}+\widehat{A B}=\widehat{B C}+\widehat{C D}\)
\(\widehat{D A B}=\widehat{D C B}\)
∴ BD divides the circle into two equal parts.
⇒ BD is a diameter of the circle.
Similarly, AC is a diameter of the circle.
(ii) Since, BD is a diameter of the circle.
∴ ∠BAD = 90° and ∠BCD = 90° [Angle in a semicircle is 90°]
Similarly, AC is a diameter of the circle.
∴ ∠ABC = 90° and ∠ADC = 90° [Angle in a semicircle is 90°]
Thus, in a quadrilateral ABCD,
∠A = ∠B = ∠C = ∠D = 90°.
Hence, ABCD is a rectangle. Proved
![]()
Question 8.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – \(\frac{1}{2}\)A, 90° – \(\frac{1}{2}\)B and 90° – \(\frac{1}{2}\)C.
Solution:
Since AD, BE and CF are the bisectors of ∠A, ∠B and ∠C respectively.
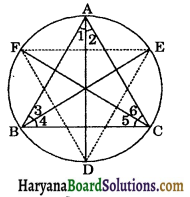
∴ ∠1 = ∠2 = \(\frac{1}{2}\)∠A
∠3 = ∠4 = \(\frac{1}{2}\)∠B …(i)
∠5 = ∠6 = \(\frac{1}{2}\)∠C ….(ii)
∠ADE = ∠3 …..(ii) [Angles in a same segment of a circle are equal]
∠ADF = ∠6 …..(i) [Angles in a same segment of a circle are equal]
Adding (ii) and (iii), we get
∠ADE + ∠ADF = ∠3 + ∠6
∠ D = \(\frac{1}{2}\)∠B + \(\frac{1}{2}\)∠C
[From (1), ∠3 = \(\frac{1}{2}\)∠B and ∠6 = \(\frac{1}{2}\)]
⇒ ∠ D = \(\frac{1}{2}\)(∠B + ∠C) ……(iv)
But, ∠A + ∠B + ∠C = 180° [Sum of angles of a triangle is 180°]
⇒ ∠B + ∠C = 180° – ∠A
⇒ \(\frac{1}{2}\)(∠B + ∠C) = \(\frac{180^{\circ}-\angle A}{2}\)
\(\frac{1}{2}\)(∠B + ∠C) = 90° – \(\frac{\angle A}{2}\)
Putting the value of \(\frac{1}{2}\)(∠B + ∠C) in (iv),
we get
∠D = 90° – \(\frac{\angle A}{2}\)
Similarly, we can prove that
∠E = 90° – \(\frac{\angle B}{2}\)
and ∠F = 90° – \(\frac{\angle C}{2}\)
Hence, angles of the ΔDEF are 90° – \(\frac{\angle A}{2}\), 90°- \(\frac{\angle B}{2}\) and 90° – \(\frac{\angle C}{2}\). Proved
Question 9.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution:
Let O and O’ be the centres of two congruent circles.
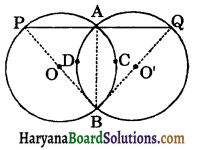
Since, AB is a common chord of the circle.
∴ \(\widehat{A C B}=\widehat{A D B}\)
⇒ ∠APB = ∠AQB
⇒ PB = BQ [Sides opposite to equal angles are equal]
Hence proved
![]()
Question 10.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Solution:
Let ABC be triangle such that o is the centre of its circumcircle. Then the perpendicular bisector of BC passes through the centre of the circumcircle. Suppose it meet circle at P. In order to prove that the perpendicular bisector of BC and the bisector of ∠A of ΔABC intersect at P. It is sufficient to prove that AP is the bisector of ∠A.
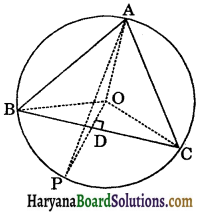
Let ∠BOC = 2x
In ΔBOD and ΔCOD, we have
BD = CD (OP is the bisector of BC)
BO = CO (Equal radii of the same circle)
OD = OD (Common).
∴ ΔBOD ≅ ΔCOD (By SAS congruence rule)
⇒ ∠BOD = ∠COD (CPCT)
⇒ ∠BOD = ∠COD = \(\frac{2 x}{2}\) = x
Arc BP subtends ∠BOP at the centre and ∠BAP at the remaining part of the circle.
∴ ∠BOP = 2∠BAP
⇒ x = 2∠BAP
[∵ ∠BOP = ∠BOD = x] …(i)
Similarly, arc CP subtends ∠COP at the centre and ∠CAP at the remaining part of the circle.
∴ ∠COP = 2∠CAP
⇒ x = 2∠CAP …..(ii)
[∵ ∠COP = ∠COD = x]
From (i) and (ii), we get
2∠BAP = 2∠CAP
⇒ ∠BAP = ∠CAP
⇒ AP is the bisector of ∠BAC.
Hence, bisector of ∠A and ⊥ bisector of BC meet at P which lies on circumcircle of ΔABC.
Hence Proved.