HBSE 9th Class Maths Important Questions Chapter 4 Linear Equations in Two Variables

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 4 Linear Equations in Two Variables Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 4 Linear Equations in Two Variables

Very Short Answer Type Questions

Question 1.
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c:
(i) 4x + 7y = 12.5
(ii) – 4x = – 5y – 9
(iii) 14 = 5x
(iv) 5x = – y
(v) 7y = 20
(vi) \(\frac{x}{3}+\frac{y}{5}\) – 13 = 0.
Solution :
(i) Writing the given equation 4x + 7y = 12.5 in the form ax + by + c = 0, we get
4x + 7y – 12.5 = 0 ……..(i)
Comparing the equation (i) with the standard form of the linear equation ax + by + c = 0, we get
a = 4, b = 7 and c = – 12.5.

(ii) Writing the given equation – 4x = – 5y – 9 in the form ax + by + c = 0, we get
– 4x + 5y + 9 = 0 ……..(i)
Comparing the equation (i) with the standard form of the linear equation ax + by + c = 0,we get a = – 4, b = 5 and c = 9.

(iii) Writing the given equation 14 = 5x in the form ax + by + c = 0, we get
5x + 0.y – 14 = 0 ……..(i)
Comparing the equation (i) with the standard form of the linear equation ax + by + c = 0, we get
a = 5, b = 0 and c = – 14.

(iv) Writing the given equation 5x = – y in the form ax + by + c = 0, we get
5x + 1.y + 0 = 0 ….(i)
Comparing the equation (i) with the standard form of the linear equation ax + by + c = 0, we get
a = 5, b = 1 and c = 0.

(v) Writing the given equation 7y = 20 in the form ax + by + c = 0, we get
0.x + 7y – 20 = 0 …(i)
Comparing the equation (i) with the standard form of the linear equation ax + by + c = 0, we get
a = 0, b = 7 and c = – 20.

(vi) Writing the given equation \(\frac{x}{3}+\frac{y}{5}\) – 13 = 0 in the form ax + by + c = 0, we get
\(\frac {1}{3}\). x + \(\frac {1}{5}\). y – 13 = 0
Comparing the equation (i) with the standard form of the linear equation ax + by + c = 0, we get
a = \(\frac {1}{3}\), b = \(\frac {1}{5}\) and c = – 13.

Question 2.
The total cost of a mobile and a computer is. ₹ 24,400. Write a linear equation in two variables to represent this statement.
Solution :
Let the cost of a mobile be Rs. x and cost of a computer be ₹ y.
According to statement, total cost of a mobile and a computer is ₹ 24,400. So, the required linear equation in two variables to represent above statement is
x + y = 24400 or x + y – 24400 = 0.

Question 3.
Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa. [NCERT Exemplar Problems]
Solution :
Let abscissa of the graph of the linear equation be x and ordinate be y.
According to question, ordinate is 3 times its abscissa. So, required linear equation is
y = 3x
⇒ 3x – y = 0.

Question 4.
The ratio of hydrogen and oxygen in water is 2 : 1. Set up a linear equation in two variables between oxygen and water.
Solution :
Let the amount of oxygen bex and the amount of water be y.
According to question,
hydrogen : oxygen= 2 : 1
⇒ oxygen : hydrogen = 1 : 2
⇒ oxygen : water = 1 : (1 + 2)
⇒ x : y = 1 : 3
⇒ \(\frac{x}{y}=\frac{1}{3}\)
⇒ 3x = y
⇒ 3x – y = 0
Hence, required linear equation in two variables is 3x – y = 0.

Question 5.
Find three different solutions for each of the following equations:
(i) 5x + 3y = 4
(ii) x + 4y = 6
(iii) 3y – 5 = 0.
Solution :
(i) We have, 5x + 3y = 4 …(i)
Substituting x = – 1 in the equation (i), we get
5 × (-1) + 3y = 4
⇒ – 5 + 3y = 4
⇒ 3y = 4 + 5 = 9
⇒ y = \(\frac {9}{3}\) = 3
∴ (- 1, 3) is a solution of the given equation.
Substituting x = 2 in the equation (1), we get
5 × 2 + 3y = 4
⇒ 10 + 3y = 4
⇒ 3y = 4 – 10 = – 6
⇒ y = \(\frac {-6}{3}\) = – 2
∴ (2, – 2) is a solution of the given equation.
Substituting x = 5 in the equation (i), we get
5 × 5 + 3y = 4
⇒ 25 + 3y = 4
⇒ 3y = 4 – 25 = – 21
⇒ y = \(\frac {-21}{3}\) = – 7
∴ (5, – 7) is a solution of the given equation.
Hence, three different solutions of the given equation are (-1, 3), (2, – 2) and (5, – 7).

Question 6.
Check which of the following are solutions of the equation 5x – 2y = 10
(i) (0, – 5)
(ii) (2, – 2)
Solution :
We have,
5x – 2y = 10
(i) Substituting x = 0, y = – 5 in the L.H.S. of equation (i), we get
L.H.S. = 5 × 0 – 2 × (-5)
= 0 + 10 = 10
= R.H.S.
∵ L.H.S. = R.H.S.
∴ (0, – 5) is a solution of the given equation.

(ii) Substituting x = 2, y = – 2 in the L.H.S. of equation (i), we get
L.H.S. = 5 × 2 – 2 × (- 2)
= 10 + 4 = 14
≠ R.H.S.
∵ L.H.S. ≠ R.H.S.
∴ (2, – 2) is not a solution of the given equation.

Question 8.
Find out which of the following equations have x = 2, y = – 1 as a
solution :
(i) 5x + 2y = 8
(ii) 4x – 3y = 14
Solution :
(i) We have, 5x + 2y = 8 …(i)
Substituting x = 2, y = – 1 in L.H.S. of the equation (i), we get
L.H.S. = 5 × 2 + 2 × (-1)
= 10 – 2 = 8
= R.H.S.
∵ L.H.S. = R.H.S.
∴ x = 2, y = – 1 is a solution of the given equation.

(ii) We have, 4x – 3y = 14 …(i)
Substituting x = 2, y = – 1 in L.H.S. of the equation (i), we get
L.H.S. = 4 × 2 – 3 × (-1)
= 8 + 3 = 11
≠ R.H.S.
∵ L.H.S. ≠ R.H.S.
∴ x = 2, y = – 1 is not a solution of the given equation.

Question 9.
Find the value of k, if x = 3, y = – 2 is a solution of the equation 4x – ky = 14.
Solution :
Since, x = 3, y = – 2 is a solution of the equation 4x – ky = 14.
Therefore, x 3, y=-2 will satisfy the given equation.
⇒ 4 × 3 – k × (-2) = 14
⇒ 12 + 2k = 14
⇒ 2k = 14 – 12 = 2
⇒ k = \(\frac {2}{2}\) = 1
Hence, k = 1.

Short Answer Type Questions

Question 1.
Find the value of k, if x = 3, y = – 4 is a solution of the equation kx + 4y = 5. Hence, find more solutions of this equations.
Solution :
Since, x = 3, y = – 4 is a solution of the equation kx + 4y = 5.
Therefore, x = 3, y = – 3 will satisfy the given equation.
⇒ k 3 + 4 × (-4) = 5
⇒ 3k – 16 = 5
⇒ 3k = 5 + 16
⇒ 3k = 21
⇒ k = \(\frac {21}{3}\) = 7
Putting the value of k in the given equation, we get
7x + 4y = 5
Substituting x = – 1 in the equation (i), we get
7 (- 1) + 4y = 5
⇒ – 7 + 4 = 5
⇒ 4y = 5 + 7 = 12
⇒ y = \(\frac {21}{4}\) = 3
∴ (- 1, 3) is a solution of the given equation.
Hence, k = 7, one more solution of the given is (- 1, 3).

Question 2.
For what value of p, the linear equation px + 5y = 8 has equal values of x and for its solution.
Solution :
We have,
px + 5y = 8
Since, given equation has equal values of x and y, then y = x
Substituting y = x in the equation (i), we
get
px + 5x = 8
⇒ px = 8 – 5x
⇒ p = \(\frac{8-5 x}{x}\)
By inspection if (1, 1) be a solution of the given equation, we have
⇒ p = \(\frac{8-5 \times 1}{x}\)
⇒ p = \(\frac{8-5}{x}\) = 3
Thus (1, 1) will be a solution of 3x + 5y = 8. If (2, 2) be a solution of the given equation, we have
p = \(\frac{8-5 \times 2}{x}\)
⇒ p = \(\frac{8-10}{2}\)
⇒ p = \(\frac {-2}{2}\) = – 1
Thus, (2, 2) will be a solution of – x + 5y = 8.

Question 3.
Determine the point on the graph of the linear equation 2x + 5y = 19, where ordinate is 1\(\frac {1}{2}\) times its abscissa.
[NCERT Exemplar Problems]
Solution :
Given linear equation is
2x + 5y = 19 ………(i)
Since, ordinate is 1\(\frac {1}{2}\) (i.e.\(\frac {3}{2}\)) times its abscissa.
Therefore, y = \(\frac {3}{2}\)x
Now, putting the value of y in equation (i) we get
2x + 5 × \(\frac {3}{2}\)x = 19
⇒ 2x + \(\frac {15x}{2}\) = 19
⇒ \(\frac{4 x+15 x}{2}\) = 19
⇒ \(\frac {19x}{2}\) = 19
⇒ x = \(\frac{19 \times 2}{19}\) = 2
and y = \(\frac {3}{2}\) × 2 = 3
Hence, required point is (2, 3).

Question 4.
Draw the graph of the linear equation whose solutions are represented by the points having the sum of the coordinates as 10 units. [NCERT Exemplar Problems]
Solution :
Let abscissa of the linear equation be x and ordinate be y, according to question
x + y = 10
⇒ y = 10 – x
When x = 3, then y = 10 – 3 = 7
When x = 4, then y = 10 – 4 = 6
When x = 5, theny = 10 – 5 = 5
Now, we prepare the table of values of (x, y)

x	3	4	5
y	7	6	5

Plotting the points A(3, 7), B(4, 6) and C(5, 5) on the graph paper and joining these points, we get a straight line AC. It is the required graph of x + y = 10.

Question 5.
Draw the graph of the equation 2y – x = 7 and determine from the graph whether x = 3, y = 2 is a solution or not.
Solution :
We have,
2y – x = 7
2y = 7 + x
y = \(\frac{7+x}{2}\)
When x = 3, then y = \(\frac{7+3}{2}=\frac{10}{2}\) = 5
When x = 1, then y = \(\frac{7+1}{2}=\frac{8}{2}\) = 4
When x = – 1, then y = \(\frac{7-1}{2}=\frac{6}{2}\) = 3
Now, we prepare the table of values of (x, y) as :

x	3	1	– 1
y	5	4	3

Plotting the points A(3, 5), B(1, 4) and C(-1, 3) on the graph paper and joining these points, we get a straight line AC. It is the required graph of 2y – x = 7.

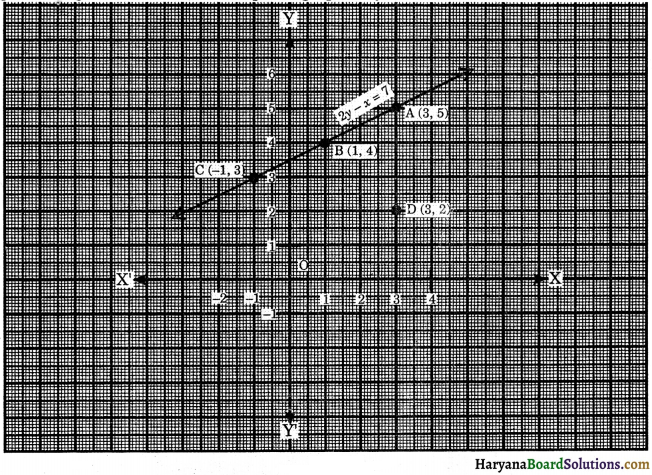
Also, plot the point D(3, 2). We observe that it does not lie on the graph of the equation 2y – x = 7.
Hence, x = 3, y = 2 is not a solution of the given equation.

Question 6.
Show that the points A(1, 2), B(-1, – 16) and C(0, – 7) lie on the graph of linear equation y = 9x – 7.
[NCERT Exemplar Problems]
Solution :
The given linear equation is
y = 9x – 7
When x = 0, then y = 9 × 0 – 7 = – 7
When x = 1, then y = 9 × 1 – 7 = 9 – 7 = 2
When x = 2, then y = 9 × 2 – 7 = 18 – 7 = 11
Now, we prepare the table of values of (x, y).

x	0	1	2
y	– 7	2	11

Plotting the points C(0, – 7), A(1, 2) and D(2, 11) on the graph paper and joining these points, we get a straight line DC and extend in both the directions. It is the required graph of y = 9x – 7.

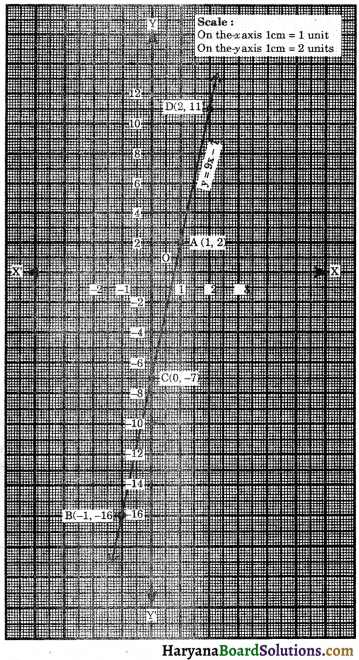
From the graph, we observe that points C(0, – 7) and A (1, 2) lie on the graph of the A equation. We plot the point B(- 1, – 16), it also lies on the graph of the given equation. Hence, the points A(1, 2), B(-1, – 16) and C(0, – 7) lie on the graph of given linear equation. Hence Proved.

Question 7.
Draw the graph of the equation x + 2y – 3 = 0. From the graph, find :
(i) x₁, the value of x, when y = 3.
(ii) y₁, the value of y, when x = 2.
Solution :
We have,
x + 2y – 3 = 0
2y = 3 – x
y = \(\frac{3-x}{2}\)
When x = 3, then
y = \(\frac{3-3}{2}=\frac{0}{2}\) = 0
When x = 1, then
y = \(\frac{3-1}{2}=\frac{2}{2}\) = 1
When x = – 1, then y = \(\frac{3+1}{2}=\frac{4}{2}\) = 2
Now, we prepare the table of values of (x, y) as :

x	3	1	– 1
y	0	1	2

Plotting the points A(3, 0), B(1, 1) and C(- 1, 2) on the graph paper and joining these points, we get a straight line AC. It is the required graph of x + 2y – 3 = 0.

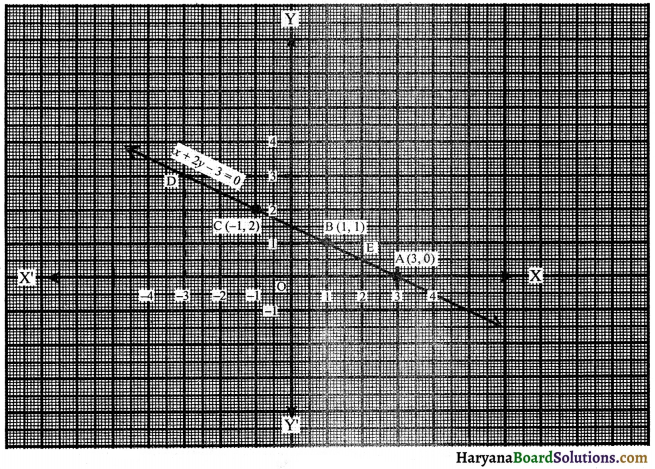
(i) To find x₁, the value of x, when y = 3. Through the point y = 3, draw a horizontal straight line which meets the straight line AC produced at D. Through the point D, draw a vertical line which meets the x-axis at x = – 3.
∴ The value of x when y = 3 is – 3, i.e., x₁ = – 3.

(ii) To find y₁, the value of y, when x = 2. Through the point x = 2, draw a vertical line which meets straight line AC at point E. Through the point E draw horizontal line which meets the y axis at y = 1/2
∴ The value of y, when x = 2 is \(\frac {1}{2}\) i.e., y₁ = \(\frac {1}{2}\).

Question 8.
A taxi charges ₹ 12 for the first km and ₹ 8 per km for subsequent distance covered. Taking the distance covered as x km and total fare ₹ y, write a linear equation for this information and, draw its graph. From the graph, find the taxi charges for convering 4 km.
Solution :
Taking the distance covered as x km and total fare as ₹ y.
Fare for first km = ₹ 12
Remaining distance = (x – 1) km
Fare for remaining distance = (x – 1) × 8
According to question, Total fare (y) = 12 + (x – 1) × 8
⇒ y = 12 + 8x – 8
⇒ y = 8x + 4
When x = 1, then y = 8 × 1 + 4 = 8 + 4 = 12
When x = 2, then y = 8 × 2 + 4 = 16 + 4 = 20
When x = 3, then y = 8 × 3 + 4 = 24 + 4 = 28
Now, we prepare the table of values of (x, y).

x	3	4	5
y	7	6	5

Plotting the points A(1, 12), B(2, 20) and C(3, 28) on the graph paper and joining these points, we get a straight line AC. It is the required graph of y = 8x + 4.
Fare for 4 km i.e., x = 4 through the point x = 4 draw a vertical line which meets the extended straight line AC at point D. Through the point D, draw horizontal line which meets the y-axis at y = 36.
Hence, linear equation is y = 8x + 4 and fare for 4 km = ₹ 36.

Long Answer Type Questions

Question 1.
Draw the graph of the equation \(\frac{x}{2}+\frac{y}{3}\) = 1
Solution :
We have,

Now, we prepare the table of values of (x, y) as :

x	0	2	4
y	3	0	– 3

Plotting the points A(0, 3), B(2, 0) and C(4, – 3) on the morph paper and joining these points, we get a striaght line AC. It is the required graph of \(\frac{x}{2}+\frac{y}{3}\) = 1.

Question 2.
Draw the graphs of the following equations :
3x + 2y – 11 = 0 and 2x – 3y + 10 = 0 Also, find the area of the triangle formed by the lines and the x-axis.
Solution :
We have,
3x + 2y – 11 = 0
⇒ 2y = – 3x + 11

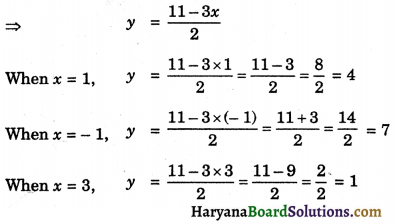
Now, we prepare the table of values of (x, y).

x	1	– 1	3
y	4	7	1

Plotting the points A(-1, 7), B(1, 4) and C(3, 1) on the graph paper and joining these points, we get a straight line AC. It is the required graph of 3x + 2y – 11 = 0.
And 2x – 3y + 10 = 0

Now, we prepare the table of values of (x, y).

x	– 2	1	4
y	2	4	6

On the graph paper plotting the points P(-2, 2), B(1, 4) and Q(4, 6), point B(1, 4) already plotted and joining these points, we get the straight line PQ. It is required graph of 2x – 3y + 10 = 0.

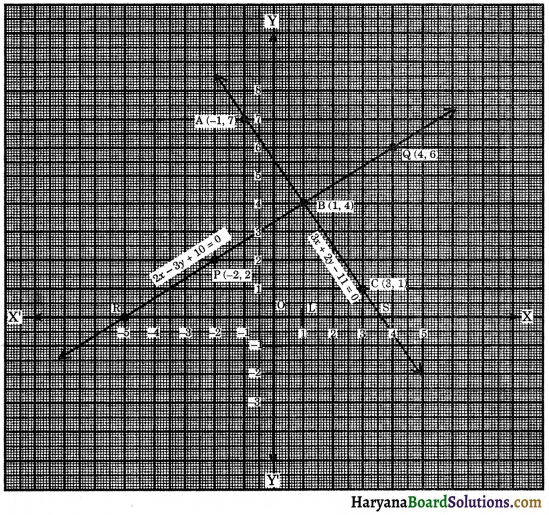
When produce the lines AC and PQ both directions they intersect at the point B and cut the x-axis at the points S and R. ΔBRS is formed. Draw BL ⊥ RS. Length of BL = 4 units and length of RS = 8.5 units.
Area of the ΔBRS = \(\frac {1}{2}\) × Base × Altitude
= \(\frac {1}{2}\) × RS × BL
= \(\frac {1}{2}\) × 8.5 × 4
= 8.5 × 2
= 17 sq. units
Hence, Area of ΔBRS = 17 sq. units.

Question 3.
Find graphically, the vertices of the triangle whose sides have the equations 2y = 8 + x, 5y = x + 14 and y – 2x – 1 = 0 respectively.
Solution :
We have,
2y = 8 + x

Now, we prepare the table of values of (x, y).

x	– 2	0	2
y	3	4	5

Plotting the points A(-2, 3), B(0, 4) and C(2, 5) on the graph paper and joining these points, we get a straight line AC. It is the required graph of 2y = 8 + x.

Now, we prepare the table of values of (x, y).

x	1	6	– 4
y	3	4	2

Plotting the points P(6, 4), Q(1, 3) and R(- 4, 2) on the graph paper and joining these points, we get a straight-line PR. It is the required graph of 5y = x + 14.
and y – 2x – 1 = 0
⇒ y = 2x + 1
When x = 1, then y = 2 × 1 + 1 = 3
When x = 2, then y = 2 × 2 + 1 = 5
When x = 3, then y = 2 × 3 + 1 = 7
Now, we prepare the table of values of (x, y).

x	1	2	3
y	3	5	7

Plotting the points Q(1, 3), C(2, 5) and M(3, 7) on the graph paper and joining these points, we get a straight line QM. The points Q(1, 3) and C(2, 5) already plotted. It is the required graph of y – 2x – 1 = 0.

Graph of the lines intersect at the points, Q, C and R : ΔCQR is the required triangle. From the graph, the co-ordinates of the vertices of the triangle are Q(1, 3), C(2, 5) and R(-4, 2).

Question 4.
In a factory, the cost of manufacturing x articles is Rs. (20 + 2x) and selling price of x articles is Rs. (2.5x). On the same graph paper with the same axes, draw two graphs, first for the cost of manufacturing against no. of articles and the second for the selling price against no. of articles.
Use your graph determine:
(i) No. of articles to be manufactured and sold to reach breakeven point (no profit and no loss situation).
(ii) The profit made when 60 articles are manufactured and sold.
Solution :
We have,
CP = ₹ (20 + 2x)
When x = ₹ 0, then CP = 20 + 2 × 0 = ₹ 20
When x = ₹ 30, then CP = 20 + 2 × 30 = 20 + 60 = ₹ 80
When x = ₹ 50, then CP = 20 + 2 × 50 = 20 + 100 = ₹ 120
When x = ₹ 80, then CP = 20 + 2 × 80 = 20 + 160 = ₹ 180
Now, we prepare the table of values of (x, CP).

x	0	30	50	80
SP	20	80	120	180

Plotting the ponts A(0, 20), B(30, 80), C(50, 120) and D(80, 180) on the graph paper and joining these points, we get a straight line AD. It is the required graph of CP = ₹ (20 + 2x).
And then SP = ₹ 2.5x
When x = ₹ 0, then SP = ₹ 0
When x = ₹ 40, then SP = 2.5 × 40 = ₹ 100
When x = ₹ 60, then SP = 2.5 × 60 = ₹ 150
When x = ₹ 80, then SP = 2.5 × 80 = ₹ 200
Now, we prepare the table of values of (x, SP).

x	0	40	60	80
SP	0	100	150	200

Plotting the points P(0, 0), Q(40, 100), R(60, 150) and S(80, 200) on the graph paper and joining these points, we get a straight line PS. It is the required graph of SP = ₹ 2.5x.
(i) The above figure shows the graph of CP and SP. Since straight lines AD and PS meets at the point Q, which x coordinate is 40, it shows that cost price of 40 articles is the same as their selling price.
Hence, no. of articles that must be manufactured and sold to reach breakeven point is 40.

(ii) Draw the vertical line through x = 60; which meets graph for CP at ₹ 140 and graph for SP at ₹ 150.
Profit = SP – CP = 150 – 140 = ₹ 10 Hence, profit = ₹ 10.

Question 5.
The ratio of girls and boys in the class is 2 : 3. Set up an equation between boys and the total students of a class and then draw its graph and find the number of boys in a class of 25 students.
Solution :
Let the total boys be x and that of students be y.
girls : boys = 2 : 3
⇒ boys : girls = 3 : 2
⇒ boys : students = 3 : (3+2)
⇒ x : y = 3 : 5
⇒ \(\frac{x}{y}=\frac{3}{5}\)
⇒ 3y = 5x
⇒ y = \(\frac {5}{3}\)x
When x = 3, then y = \(\frac {5}{3}\) × 3 = 5
When x = 6, then y = \(\frac {5}{3}\) × 6 = 10
When x = 9, then y = \(\frac {5}{3}\) × 9 = 15
Now, we prepare the table of values of (x, y) as :

x	3	6	9
y	5	10	15

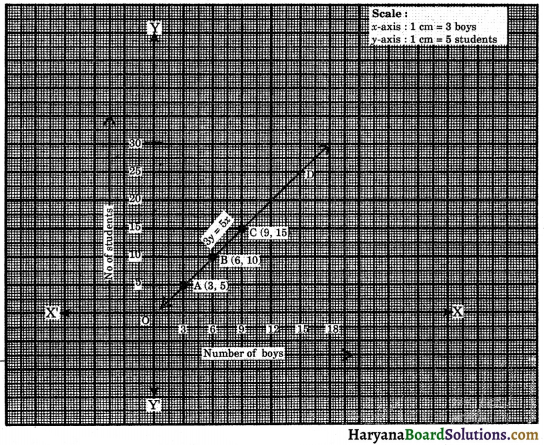
Plotting the points A(3, 5), B(6, 10) and C(9, 15) on the graph paper and joining these points, we get a straight line AC. It is the required graph of 3y = 5x.
Total number of students = 25 i.e., y = 25
Through the point y = 25, draw a horizontal line which meets straight line AC produced at the point D. Through the point D draw a vertical line which meets at x-axis at x = 15.
Hence, linear equation is 5x – 3y = 0 and number of boys out of 25 students = 15.

Question 6.
The cost of diesel in a city is ₹ 45 per litre. Set up a linear equation with x representing quantity of diesel (in litres) purchased and y representing the total cost (in ₹) and draw its graph.
Solution :
Cost of 1 litre diesel = ₹ 45
Cost of x litres diesel = ₹ 45x
Cost of x litres diesel = ₹ y
∴ y = 45x
When x = 1, then y = 45 × 1 = 45
When x = 2, then y = 45 × 2 = 90
When x = 3, then y = 45 × 3 = 135
Now, we prepare the table of values of (x, y) as :

x	1	2	3
y	45	90	135

Plotting the points A(1, 45), B(2, 90) and C(3, 135) on the graph paper and joining these points, we get a straight line AC. It is the required graph of y = 45x.

Hence, the linear equation is y – 45x = 0.

Question 7.
60% of the students in a school are boys and remaining are girls. Set up an equation and draw the graph representing the number of boys and girls. By reading the graph, find :
(i) Number of boys if girls are 16.
(ii) Number of girls if boys are 18.
Solution :
Let the number of boys be x and number of girls be y.
∴ Total number of students = x + y
According to question, x = 60% of (x + y)
⇒ x = \(\frac {60}{100}\) × (x + y) ⇒ x = \(\frac {3}{5}\) (x + y)
⇒ 5x = 3x + 3y ⇒ 5x – 3x = 3y
⇒ 2x = 3y ⇒ y = \(\frac {2}{3}\)x
When x = 3, then y = \(\frac {2}{3}\) × 3 = 2
When x = 9, then y = \(\frac {2}{3}\) × 9 = 6
When x = 15, then y = \(\frac {2}{3}\) × 15 = 10
Now, we prepare the table of values of (x, y) as :

x	3	9	15
y	2	6	10

Plotting the points A(3, 2), B(9, 6) and C(15, 10) on the graph paper and joining these points, we get a straight line AC. It is the required graph of 2x = 3y.

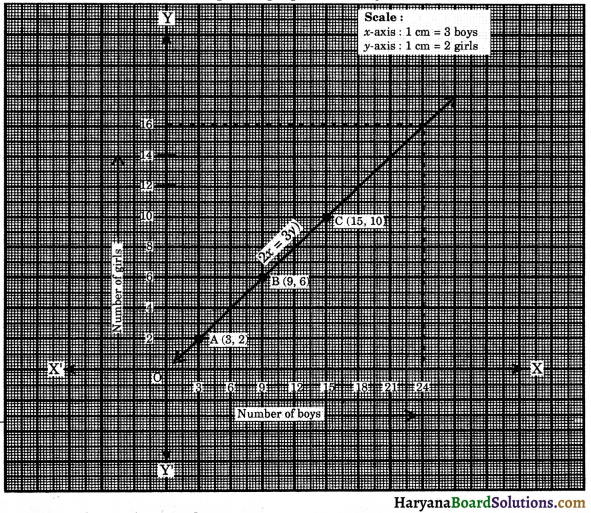
From the graph we observe that :
(i) If girls are 16, then number of boys = 24
(ii) If boys are 18, then number of girls = 12
Linear equation is
2x – 3y = 0.

Multiple Choice Questions

Choose the correct option in each of the following:

Question 1.
Any point on x-axis is of the form:
[NCERT Exemplar Problems]
(a) (x, y), where x ≠ 0, y ≠ 0
(b) (x, 0), where x ≠ 0
(c) (0, y), where y ≠ 0
(d) (y, y), where y ≠ 0
Solution :
(b) (x, 0), where x ≠ 0

Question 2.
Any point on y-axis is of the form:
[NCERT Exemplar Problems]
(a) (x, y), where x ≠ 0, y ≠ 0
(b) (0, y), where y ≠ o
(c) (x, 0), where x ≠ 0
(d) (x, x), where x ≠ 0
Solution :
(b) (0, y), where y ≠ o

Question 3.
The equation x – 5 = 0 represents the line:
(a) parallel to y-axis
(b) parallel to x-axis
(c) passes through origin
(d) is perpendicular to y-axis
Solution :
(a) parallel to y-axis

Question 4.
The equation 2y = – 5 represents the line:
(a) parallel to y-axis
(b) passes through origin
(c) parallel to x-axis
(d) perpendicular to x-axis
Solution :
(c) parallel to x-axis

Question 5.
If x = 1, y = 1 is a solution of the equation ax – 2y = 10, then value of a is :
(a) 10
(b) 8
(c) 12
(d) 14
Solution :
(c) 12

Question 6.
If x = – 1, y = 3 is a solution of the equation 5x + ay = 4, then value of a is :
(a) 3
(b) 4
(c) 5
(d) 9
Solution :
(a) 3

Question 7.
y = 0 is the equation of
(a) x-axis
(b) y-axis
(c) both x-axis and y-axis
(d) a line parallel to y-axis
Solution :
(a) x-axis

Question 8.
x = 0 is the equation of:
(a) x-axis
(b) y-axis
(c) both r-axis and y-axis
(d) a line parallel to x-axis
Solution :
(b) y-axis

Question 9.
The graph of the linear equation 5x + 2y = 10 cut the x-axis at the point:
(a) (2, 0)
(b) (0, 2)
(c) (0, – 5)
(d) (-5, 0)
Solution :
(a) (2, 0)

Question 10.
The graph of the linear equation 2x + 3y = 6 cuts they axis at the point:
[NCERT Exemplar Problems]
(a) (0, 2)
(b) (2,0)
(c) (0, 3)
(d) (3, 0)
Solution :
(a) (0, 2)