HBSE 9th Class Maths Important Questions Chapter 10 Circles

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 10 Circles Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 10 Circles

Very Short Answer Type Questions

Question 1.
AB and CD are two parallel chords of a circle whose diameter is BC. Prove that AB = CD.
Solution:
Since AB || CD and transversal BC cuts them.

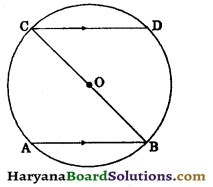
∴ ∠ABC = ∠DCB
(Alternate interior angles)
\(\widehat{A C}=\widehat{B D}\) …(i)
[∵ Equal arcs of a circle subtends equal angles at the circumference]
Since BC is a diameter.

⇒ chord AB = chord CD.
Hence proved

Question 2.
In the given figure, if O is the centre of a circle and OP is perpendicular to the chord AC. Show that BC = 20P.

Solution:
Since O is the centre of a circle.
∴ O is the mid point of AB and OP ⊥ AC.
AP = PC [By theorem 10.3]
⇒ P is the mid point of AC.
Thus O is the mid point of AB and Pis the mid point of AC.
⇒ OP || BC and OP = \(\frac{1}{2}\)BC
[By mid point theorem]
⇒ BC = 20P. Hence proved

Question 3.
Two circles whose centres are O and O’ intersecting at P and Q. Through P, a straight line l parallel to OO’ is drawn to meets the circles at A and B. If M is the mid point of OO’, prove that AP = PB.

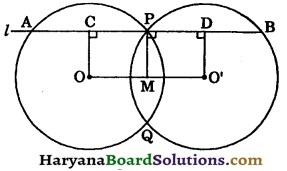
Solution:
Draw
OC ⊥ AB
O’D ⊥ AB and MP ⊥ AB
Since OC ⊥ AB, MP ⊥ AB and O’D ⊥ AB.
OC || MP || O’D
and M is the mid point of OO’.
∴ P is the mid point of CD.
⇒ CP = PD ….(i)
∵ OC ⊥ AP and AP is a chord.
∴ AC = CP ….(ii)
O’D ⊥ PB and PB is a chord.
∴ BD = PD ….(iii)
From (i), (ii) and (iii), we get
AC = CP = PD = BD …(iv)
⇒ AC = PD [using (iv)]
⇒ 2AC = 2PD
⇒ AP = PB Hence proved

Question 4.
Prove that a diameter is the longest chord in a circle.
Solution:
Given: AB is a diameter of a circle C(O, r) and CD is a chord of the circle.

To prove : Diameter
AB > chord CD.
Proof : Since diameter passes through the centre.
∴ Diameter is nearer to the centre than chord CD.
But, of any two chords of a circle, the one which is nearer to the centre is larger.
∴ AB > CD
Hence, a diameter is the longest chord in a circle.
Proved

Question 5.
In the given figure, AB is a diameter of the circle whose centre is O. If ∠ADC = 120°, calculate the ∠BAC.

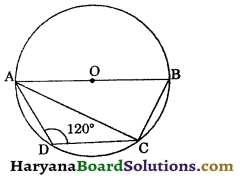
Solution:
Since, AB is a diameter of the circle.
∠ACB = 90° [∵ Angle in a semicircle is 90°]
Since, ABCD is a cyclic quadrilateral.
∠ABC + ∠ADC = 180°
[∵ sum of opposite angles of cyclic quadrilateral is 180°]
⇒ ∠ABC + 120° = 180°
⇒ ∠ABC = 180° – 120° = 60°
In right ΔACB, we have
∠ACB + ∠ABC + ∠BAC = 180°
[∵ sum of angles of a triangle is 180°]
⇒ 90° + 60° + ∠BAC = 180°
⇒ 150° + ∠BAC = 180°
⇒ ∠BAC = 180° – 150°
Hence, ∠BAC = 30°.

Question 6.
In the given figure, ∠ACB = 45° and ∠BDC = 40°. Calculate ∠CAB and ∠ABC.

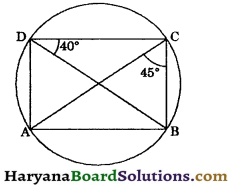
Solution:
∠CAB = ∠BDC [∵ Angles in a same segment are equal]
⇒ ∠CAB = 40°
In ΔABC, we have
∠CAB + ∠ABC + ∠ACB = 180°
[sum of angles of a triangle is 180°]
⇒ 40° + ∠ABC + 45o = 180°
⇒ 85° + ∠ABC = 180°
⇒ ∠ABC = 180° – 85°
⇒ ∠ABC = 95°
Hence ∠CAB = 40° and ∠ABC = 95o.

Question 7.
In the given figure, ∠BAD = 88°. Find the values of x and y.

Solution:
Since, ABCD is a cyclic quadrilateral.
∴ ∠BCD + ∠BAD = 180°
[∵ sum of opp. angles of a cyclic quadrilateral is 180°]
⇒ x + 88° = 180°
⇒ x = 180° – 88°
⇒ x = 92°
⇒ ∠BCD + ∠FCD= 180°
(By linear pair axiom)
⇒ 92° + ∠FCD = 180°
⇒ ∠FCD = 180° – 92° = 88°
Since, CDEF is a cyclic quadrilateral.
∴ ∠FCD + ∠FED = 180°
⇒ 88° + ∠FED = 180°
⇒ ∠FED = 180° – 88°
⇒ ∠FED = 92°
⇒ ∠y = 92°
Hence, x = 92° and y = 92°.

Question 8.
An equilateral triangle of side 8 cm is inscribed in a circle. Find the radius of the circle.
Solution:
Let ABC be an equilateral triangle of side 8 cm and AD be its median.

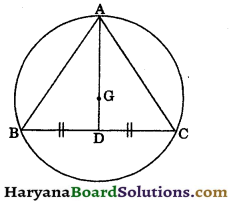
Let G be centroid of AABC, then

⇒ \(\frac{A D}{A G}=\frac{3}{2}\)
⇒ \(\frac{A G}{A D}=\frac{2}{3}\)
⇒ AG = \(\frac{2}{3}\)AD …….(i)
Since, D is the mid point of BC i.e.,
BD = CD.
∴ AD ⊥ BC [By theorem 10.4]
We know that in an equilateral triangle centroid coincides with the circumcentre.
Therefore G is the circumcentre with circumradius GA.
BD = \(\frac{1}{2}\)BC
⇒ BD = \(\frac{1}{2}\) × 8 = 4 cm
In right ΔADB, we have
⇒ AB² = BD² + AD²
(By Pythagoras theorem)
⇒ 8² = 4² + AD²
⇒ 8² – 4² = AD²
⇒ (8 + 4) (8 – 4) = AD²
⇒ 12 × 4 = AD²
⇒ AD² = 48
⇒ AD = \(\sqrt{48}=\sqrt{4 \times 4 \times 3}\)
= 4\(\sqrt{3}\) cm
AG = \(\frac{2}{3}\)AD [From (i)]
⇒ AG = \(\frac{2}{3} \times 4 \sqrt{3}\)
⇒ \(\frac{8 \sqrt{3}}{3}\)
Hence,radius of the circle = \(\frac{8 \sqrt{3}}{3}\) cm.

Short Answer Type Questions

Question 1.
AB and CD are two chords of a circle such that AB = 24 cm and CD= 32 cm and AB || CD. If the distance between AB and CD is 4 cm, find the radius of the circle.
Solution:
Draw OP ⊥ AB, OQ ⊥ CD and join OA and OC.
Since, OP ⊥ AB
∴ AP = PB = \(\frac{1}{2}\)AB
(By theorem 10.3)
AP = \(\frac{1}{2}\) × 24 = 12 cm
Again, OQ ⊥ CD
∴ CQ = QD = \(\frac{1}{2}\)CD
(By theorem 10.3)
∴ CQ = \(\frac{1}{2}\) × 32 = 16 cm

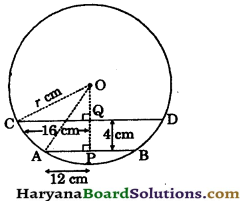
Let radius of the circle be r сm and OQ be x cm.
In right triangle OPA, we have
OA² = AP² + OP²
(By Pythagoras theorem)
⇒ r² = 12² + (OQ + QP)²
⇒ r² = 144 + (x + 4)²
⇒ r² = 144 + x² + 16 + 8x
⇒ r² = 160 + x² + 8x …(i)
In right ΔOQC, we have
CO² = CQ² + OQ²
⇒ r² = 16² + x² …(ii)
From (i) and (ii), we get
⇒ 160 + x² + 8x = 16² + x²
⇒ 160 + 8x = 256
⇒ 8x = 256 – 160
⇒ 8x = 96
⇒ x = \(\frac{96}{8}\) = 12 cm
Putting the value of x in equation (ii), we get
r² = 16² + (12)²
⇒ r² = 256 + 144
⇒ r² = 400
⇒ r= \(\sqrt{400}=\sqrt{20 \times 20}\)
= 20 cm
Hence,radius of the circle = 20 cm.

Question 2.
In the given figure, AB and CD are two parallel chords of a circle whose centre is O, such that AB = 30 cm, AO = OC = 17 cm, OM ⊥ AB, ON ⊥ CD and distance between AB and CD is 23 cm. Find the length of chord CD.

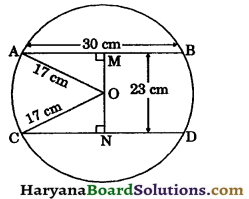
Solution:
Since,
OM ⊥ AB
AM = MB = \(\frac{1}{2}\)AB
⇒ AM = \(\frac{1}{2}\) × 30 = 15 cm
In right ΔOMA, we have
AO² = AM² + OM²
(By Pythagoras theorem)
⇒ 17² = 15² + OM²
⇒ 17² – 15² = OM²
⇒ (17 + 15) (17 – 15) = OM²
⇒ 32 × 2 = OM²
⇒ OM = \(\sqrt{32 \times 2}=\sqrt{4 \times 4 \times 2 \times 2}\)
⇒ OM = 8 cm
Distance between AB and CD is 23 cm i.e.,
MN = 23 cm
ON = MN – OM
⇒ ON = 23 – 8 = 15 cm
In right ΔONC, we have
OC² = CN² + ON²
⇒ 17² = CN² + 15²
⇒ CN² = 17² – 15²
⇒ CN² = (17 + 15) (17 – 15)
⇒ CN² = 32 × 2 = 64
⇒ CN = \(\sqrt{64}\) = 8 cm
Since, ON ⊥ CD
⇒ CN = \(\frac{1}{2}\)CD
⇒ 8 = \(\frac{1}{2}\)CD
⇒ CD = 8 × 2 = 16 cm
Hence,length of chord CD = 16 cm.

Question 3.
Of any two chords of a circle, show that the one which is nearer to the centre is larger.
Solution:
Given: Two chords AB and CD of a circle C(O, r), OP ⊥ AB and OQ ⊥ CD such that
OP < OQ.

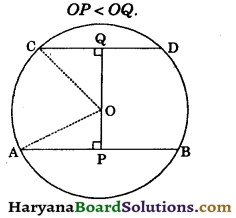
To prove: AB > CD.
Construction : Join OA and OC.
Proof : Since OP ⊥ AB and OQ ⊥ CD.
AP = \(\frac{1}{2}\)AB and CQ = \(\frac{1}{2}\)CD ……..(i)
Since, OA = OC = r
OP < OQ (given)
⇒ OQ > OP
⇒ OQ² > OP² …(i)
In right ΔOPA and ΔOQC, we have
OA² = OP² + AP²
and CO² = OQ² + CQ²
⇒ OP² + AP² = OQ² + CQ² [∵ OA = OC = r]
⇒ OP² + AP² = OQ² + CQ² > OP² + CQ² [using (ii)]
⇒ OP² + AP² > OP² +CQ²
⇒ AP² > CQ²
⇒ AP > CQ
⇒ 2AP > 2CQ
⇒ AB > CD [using (i)]
Hence AB > CD. Proved

Question 4.
In the given figure, O is the centre of the circle. Prove that ∠a = ∠b + ∠c.

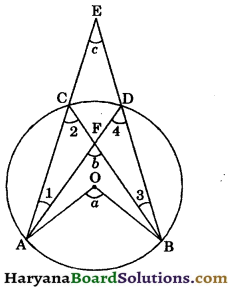
Solution:
In ΔACF, we have
∠b = ∠1 + ∠2 [∵ Exterior angle is equal to sum of its two opposite interior angles]
⇒ ∠2 = ∠b – ∠1 …..(i)
In ΔAED, we have
∠4 = ∠1 + ∠c …(ii)
[∵ Exterior angle is equal to sum of it opposite two interior angles]
∠2 = ∠4 ……(iii)
[Angles in a same segment of a circle are equal]
Arc AB subtends ∠a at the centre and ∠2 at the remaining part of the circle.
∴ ∠a = 2∠2
⇒ ∠a = ∠2 + ∠2
⇒ ∠a = ∠2 + ∠4 [Using (iii)]
⇒ ∠a = ∠b – ∠1 + ∠1 + ∠c [Using (ii) and (iii)]
⇒ ∠a = ∠b + ∠c.
Hence proved

Question 5.
Prove that the line joining the mid points of two parallel chords of a circle passes through the centre.
Solution:
Given : AB and CD are two parallel chords of a circle whose centre is O. P and Q are the mid points of AB and CD respectively.

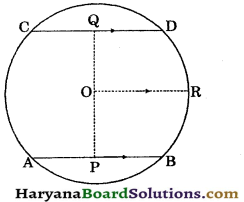
To prove : PQ is a straight line.
Construction : Join OP and OQ, draw OR || AB
but CD || AB ∴ OR || CD.
Proof : Since P is the mid point of AB.
∴ OP ⊥ AB [By theorem 10.4]
⇒ ∠APO = 90°
Again, Q is the mid point of CD.
∴ OQ ⊥ CD
⇒ OQC = 90°
∴ OR || CD (By construction)
∠QOR = ∠OQC
(Alternate interior angles)
⇒ ∠QOR = 90°
and OR || AB
∠POR = ∠APO
(Alternate interior angles)
⇒ ∠POR = 90° …..(ii)
Adding (i) and (ii), we get
∠QOR + ∠POR = 90° + 90°
⇒ ∠QOP = 180°
∴ POQ is a straight line. Hence proved

Question 6.
In the given figure, a diameter AB of a circle bisects a chord CD. If AD || BC, prove that chord CD is also a diameter of the circle.

Solution:
Given : A circle with centre o in which diameter AB bisects chord CD and AD || BC.
To prove : CD is also a diameter of the circle.
Proof: Since AD || BC and transversal CD cut them.
∴ ∠ADC = ∠BCD
(Alternate interior angles)
⇒ ∠ADO = ∠BCO
In ΔBOC and ΔAOD, we have
∠BCO = ∠ADO
(As proved above)
CO = OD[∵ AB bisects CD]
∠BOC = ∠AOD
(Vertically opposite angles)
∴ ΔΒΟC ≅ ΔΑOD (By ASA congruence rule)
⇒ CO = OD
∴ O is the mid point of CD.
∵ O is the centre of circle.
So, CD is also a diameter of the circle.
Hence proved

Question 7.
AB and CD are equal chords of a circle with centre 0, when produced these chords meet at P. Prove that : [NCERT Exemplar Problems]
(i) PB = PD
(ii) AP = PC.
Solution:
Given : AB and CD are equal chords of a circle and when produced AB and CD meet at P.

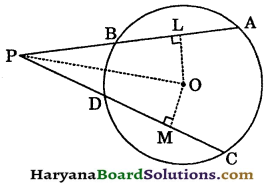
To prove : (i) PB = PD
(ii) AP= PC.
Construction : Draw OL ⊥ AB and OM ⊥ CD.
Proof : Since OL ⊥ AB and OM ⊥ CD.
∴ L is the mid point of AB and M is the mid point of CD.
∵ AB = CD (given)
⇒ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)CD
⇒ AL = CM and BL =DM…(i)
∵ AB = CD
∴ OL = OM …(ii)
[∵ Equal chords are equidistant from the centre]
In right ΔOLP and ΔOMP, we have
∠OLP = ∠OMP (Each is 90°)
hyp. OP= hyp. OP (common)
OL = OM [As proved in (ii)]
∴ ΔOLP ≅ ΔOMP [By RHS congruence rule]
⇒ PL = PM (CPCT) … (iii)
Subtracting (i) from (iii), we get
PL – BL = PM – DM
⇒ PB = PD
Adding (i) and (iii), we get
AL + PL = CM + PM
⇒ AP = PC
Hence, (i) PB = PD (ii) AP = PC. Proved

Question 8.
In an equilateral triangle, prove that the centroid and the circumcentre coincide.
Solution:
Given : An equilateral triangle ABC such that D, E and Fare respectively the mid points of the sides BC, CA and AB.

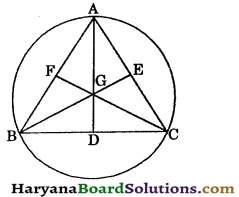
To prove: The centroid and circumcentre are coincide.
Construction : Draw medians AD, BE and CF.
Proof : Let medians AD, BE and CF intersect at G. So, G is the centroid of ΔABC.
∵ ABC is an equilateral triangle
∴ AB = BC = CA
⇒ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)BC = \(\frac{1}{2}\)CA
⇒ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)CA
⇒ BF = CE ……(i)
In ΔBFC and ΔCEB, we have
BF = CE [As proved in (i)]
∠B = ∠C [Each = 60°]
BC = BC [Common]
∴ ΔBFC ≅ ΔCEB
(By SAS congruence rule)
⇒ CF = BE (CPCT) … (ii)
Similarly, ΔABD ≅ ΔBCE
(By SAS congruence rule)
⇒ AD = BE (CPCT) …(iii)
From (ii) and (iii), we get
AD = BE = CF ….(iv)
But we know that centroid divide the medians in the ratio 2 : 1. So the centroid is the point located at \(\frac{2}{3}\) of the distance from a vertex along a median. The centre of the circumcircle of this triangle is called the circumcentre.
From (iv), we get
AD = BE = CF
⇒ \(\frac{2}{3}\)AD = \(\frac{2}{3}\)BE = \(\frac{2}{3}\)CF
⇒ GA = GB = GC
⇒ G is the equidistant from the vertices.
⇒ G is the circumcentre of the ΔABC.
Hence, G is the centroid as well as circumcentre of ΔABC.
Proved

Question 9.
In the given figure, OA, OB and OD are radii of the circle and AB is a chord when DO and AB are produced meet at point C such that OB = BC. Prove that b° = \(\frac{1}{3}\)a°.

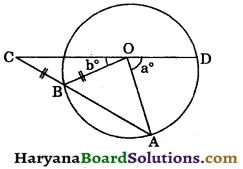
Solution:
Since, OB = BC (given)
∠BCO = ∠BOC = b° …(i)
[Angles opp. to equal sides are equal]
In ΔOBC, we have
∠OBA = ∠BCO + ∠BOC
[Exterior angle is equal to sum of two opposite interior angles]
∠OBA = b° +6° = 2b°
In ΔOBA, we have
OB = OA [Radii of the same circle]
⇒ ∠OBA = ∠OAB
⇒ 2b° = ∠OAB
⇒ ∠OAB = 2b° ……(ii)
Now in ΔOCA, we have
∠AOD = ∠OCA + ∠OAC
∠AOD = b° + 2b° [using (i) and (ii)]
a° = 3b°
b° = \(\frac{1}{3}\)a°
Hence proved

Question 10.
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90°. [NCERT Exemplar Problems]
Solution:
Let O be the circumcentre of triangle ABC.
Join BO and CO.
∵ OB = OC (equal radii of same circle)
⇒ ∠OBC = ∠OCB …..(i)
(Angles opp. to equal sides are equal)
Since, arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.

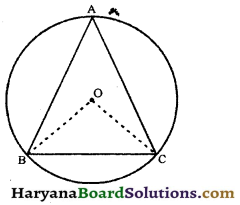
Therefore, ∠BOC = 2∠BAC …..(ii)
(By theorem 10.8)
In ΔBOC, we have
∠OBC + ∠OCB + ∠BOC = 180°,
[∵ Sum of angles of a triangle is 180°]
⇒ ∠OBC + ∠OBC + 2∠BAC = 180° [Using (i) and (ii)]
⇒ 2∠OBC + 2∠BAC = 180°
⇒ 2(∠OBC + ∠BAC)= 180°
⇒ ∠OBC + ∠BAC = \(\frac{180^{\circ}}{2}\)
⇒ ∠OBC + ∠BAC = 90° Hence proved

Question 11.
Prove that the circle drawn on any one equal sides of an isosceles triangle as diameter, bisects the base.
Solution:
Given: A triangle ABC in which AB = AC and a circle is drawn by taking AB as diameter intersecting BC at D.

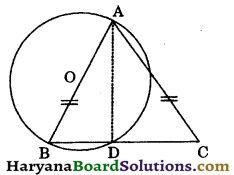
To prove: BD = CD.
Construction : Join AD.
Proof : ∠ADB = 90°
(Angle in a semicircle is 90°)
But, ∠ADB + ∠ADC = 180°
(By linear pair axiom)
⇒ 90° + ∠ADC = 180°
⇒ ∠ADC = 180° – 90°
⇒ ∠ADC = 90°
In ΔADB and ΔADC, we have
∠ADB = ∠ADC [Each is 90°]
Hyp. AB = Hyp. AC (given)
AD = AD (Common)
∴ ΔADB ≅ ΔADC
(By RHS congruence rule)
⇒ BD = CD (CPCT)
Hence, BD = CD. Proved

Question 12.
In the given figure, AB and CD are chords of a circle whose centre is O. If AB and CD intersect at P inside the circle. Prove that ∠AOC + ∠BOD = 2∠BPD.

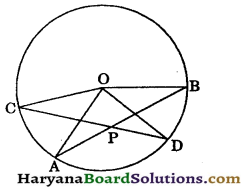
Solution:
Join AD.
Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle.
∠AOC = 2∠ADC ….(i)
[By theorem 10.8]

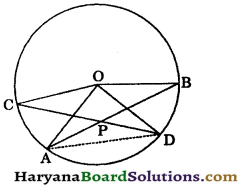
Similarly, arc BD subtends ∠BOD at the centre and ∠BAD at remaining part of the circle.
∴ ∠BOD = 2∠BAD …(ii)
Adding (i) and (ii), we get
∠AOC + ∠BOD = 2∠ADC + 2∠BAD
∠AOC + ∠BOD = 2(∠ADP + ∠DAP) … (iii)
In ΔAPD, we have
∠BPD = ∠ADP + ∠DAP
[∵ Exterior angle is equal to sum of its two opp. interior angles]
⇒ 2∠BPD = 2(∠ADP + ∠DAP)…(iv)
From (iii) and (iv), we get
∠AOC + ∠BOD = 2∠BPD. Hence proved

Question 13.
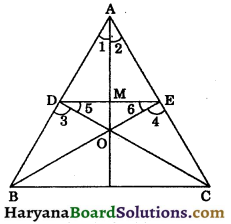
D and E are respectively the points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that points B, C, E and D are concyclic.
OR
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic. [NCERT Exemplar Problems]
Solution:
In ΔABC, we have
AB = AC (given)
⇒ ∠B = ∠C [Angles opposite to equal sides are equal]
In ΔADE, we have

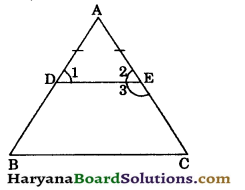
AD = AE (given)
⇒ ∠1 = ∠2 [Angles opp. to equal sides are equal]
In ΔABC, we have
∠A + ∠B + ∠C = 180° …….(i)
[∵ Sum of angles of a triangle is 180°]
In ΔADE, we have
∠A + ∠1 + ∠2 = 180° …..(ii)
From (i) and (ii), we get
∠A + ∠B + ∠C = ∠A + ∠1 + ∠2
⇒ ∠B + ∠C = ∠1 + ∠2
⇒ ∠B + ∠B = ∠2 + ∠2
[∵ ∠C = ∠B and ∠1 = ∠2]
⇒ 2∠B = 2∠2
⇒ ∠B = ∠2
⇒ ∠B = 180° – ∠3
[∵ ∠2 + ∠3 = 180° (By linear pair axiom)
⇒ ∠2 = 180° – ∠3]
⇒ ∠B + ∠3 = 180° – ∠3 + ∠3
[Adding ∠3 on both sides]
⇒ ∠B + ∠DEC = 180°
Similarly, ∠C + ∠BDE = 180°
Thus, in a quadrilateral BCED, sum of opposite angles is 180°.
Therefore, quadrilateral BCED is cyclic.
Hence, B, C, E and D are concyclic. Proved

Question 14.
ABCD is a cyclic quadrilateral in which AD and BC when produced meet at P such that AP = PB. Prove that :
(i) ABCD is a cyclic trapezium
(ii) DP = CP.
Solution:
Given : A cyclic quadrilateral ABCD in which AD and BC when produced meet at P such that AP = PB.

To prove: (i) ABCD is a cyclic trapezium.
(ii) DP = CP.
Proof: In ΔPAB, we have
AP = PB (given)
⇒ ∠A = ∠B [Angles opposite to equal sides are equal]
∵ ABCD is a cyclic quadrilateral
∴ ∠A + ∠C = 180°
[Sum of opp. angles of a cyclic quad. is 180°]
⇒ ∠B + ∠C = 180° [∵ ∠A = ∠B]
But, these are consecutive interior angles.
∴ AB || CD
⇒ ABCD is cyclic trapezium.
Now, AB || CD and a transversal PB cuts them,
∠1 = ∠B …..(ii) (Corresponding angles)
Again, AB || CD and a transversal AP cuts them
∠3 = ∠A …..(iii) (Corresponding angles)
From (i), (ii) and (iii), we get
∠3 = ∠1
⇒ DP = CP [Sides opposite to equal angles are equal]
Hence, (i) ABCD is a cyclic trapezium, (ii) DP = CP.
Hence Proved

Question 15.
The diagonals AC and BD of cyclic quadrilateral ABCD intersect at right angles at E (see in figure). A line l through E and perpendicular to AB meets CD at F. Prove that F is the mid point of CD.

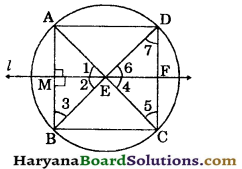
Solution:
Given : The diagonals AC and BD of a cyclic quadrilateral ABCD intersect at 90° at E. A line l through E and ⊥ to AB meets CD at F.
To prove: CF = DF.
Proof: ∠AEB = 90°
[∵ AC and BD intersect at 90°]
⇒ ∠1 + ∠2 = 90° …..(i)
EM ⊥ AB (given).
In right AEMB, we have
∠2 + ∠3 + ∠EMB = 180°
[∵ Sum of angles of a triangle is 180°]
⇒ ∠2 + ∠3 +90° = 180°
⇒ ∠2 + ∠3 = 180° – 90°
⇒ ∠2 + ∠3 = 90° ……(ii)
From (i) and (ii), we get
∠1 + ∠2 = ∠2 + ∠3
⇒ ∠1 = ∠3 …..(iii)
But, ∠1 = ∠4 ….(iv)
(Vertically opposite angles)
and ∠5 = ∠3 ……(v)
(Angles in a same segment are equal).
From (iii), (iv) and (v), we get
∠4 = ∠5
⇒ EF = FC …..(vi)
[Sides opp. to equal angles are equal]
Similarly, ∠6 = ∠7 3
⇒ EF = FD…(7)
From (vi) and (7), we get
CF = DF. Hence proved

Question 16.
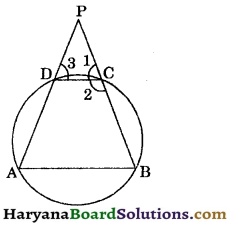
The bisector of ∠B of an isosceles triangle ABC with AB = AC meets the circumcircle of ΔABC at P (see in figure). If AP and BC are produced meet at Q, prove that CQ = CA,

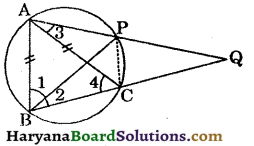
Solution:
Join CP.
∠1 = ∠2 (BP is the bisector of ∠B)
∠3 = ∠2 …..(ii)
(Angles in a same segment are equal)
AB = AC (given)
∠B = ∠4 (Angles opp. to equal sides are equa)
⇒ ∠1 + ∠2 = ∠4
⇒ ∠2 + ∠2 = ∠4 [∵ ∠1 = ∠2]
⇒ ∠4 = 2∠2
⇒ ∠4 = 2∠3
[From (ii), ∠2 = ∠3) …(iii)
In ΔACQ, we have
∠ACB = ∠3 + ∠Q
[∵ Exterior angle is equal to sum of its two opposite interior angles
⇒ ∠4 = ∠3 + ∠Q
⇒ 2∠3 = ∠3 + ∠Q
[From (iii), ∠4 = 2∠3]
⇒ 2∠3 – ∠3 = ∠Q
⇒ ∠3 = ∠Q
⇒ AC = CQ [Sides opposite to equal angles are equal]
⇒ CQ = CA. Hence proved

Question 17.
Prove that the sum of the angles in the four segments exterior to a cyclic quadrilateral is equal to 6 right angles.

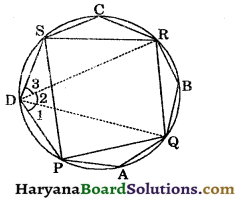
Solution:
Given : A cyclic quadrilateral PQRS and angles A, B, C and D are in the four external segments.
To prove: ∠A + ∠B + ∠C + ∠D = 6 right angles.
Construction : Join DR and DQ.
Proof : Since, PAQD is a cyclic quadrilateral.
∠1 + ∠A = 180° ……(i)
[Sum of opp. angles of cyclic quadrilateral is 180°]
Similarly, ∠2 + ∠B = 180° …..(ii)
and ∠3 + ∠C = 180° …..(iii)
Adding (i), (ii) and (iii), we get
∠1 + ∠A + ∠2 + ∠B + ∠3 + ∠C = 180° + 180° + 180°
⇒ ∠A + ∠B + ∠C + ∠1 + ∠2 + ∠3 = 540°
⇒ ∠A + ∠B + ∠C + ∠D = 540°
[∵ ∠1 + ∠2 + ∠3 = ∠D]
⇒ ∠A + ∠B + ∠C + ∠D = 6 × 90°
Hence, ∠A + ∠B + ∠C + ∠D = 6 right angles.
Proved

Question 18.
If two sides of a cyclic quadrilateral are parallel, prove that:
(i) remaining two sides are equal.
(ii) both diagonals are equal.
Solution:
Given : A cyclic quadrilateral ABCD in which AB || CD.
To prove: (i) AD = BC, (ii) AC = BD.

Proof: Since, ABCD is cyclic quadrilateral.
∴ ∠BAD + ∠BCD = 180° …(i)
[Sum of opp. angles of cyclic quadrilateral is 180°]
AB || CD and a transversal BC cuts them.
∴ ∠ABC + ∠BCD = 180° …(ii)
[∵ Consecutive interior angles are supplementary]
From (i) and (ii), we get
∠BAD + ∠BCD = ∠ABC + ∠BCD
∠BAD = ∠ABC …..(iii)
Now in ΔADB and ΔBCA, we have
∠BAD = ∠ABC
[As proved above in (iii)]
∠ADB = ∠BCA [Angles in a same segments are equal]
AB = AB (Common)
∴ ΔDAB ≅ ΔBCA
(By AAS congruence rule)
⇒ AD = BC (CPCT)
and BD = AC (CPCT)
Hence, (i) AD = BC, (ii) AC = BD. Proved.

Long Answer Type Questions

Question 1.
In the given figure, two circles of radii 10 cm and 12 cm intersect each other at A and B. If the length of common chord is 16 cm, find the distance between their centres.

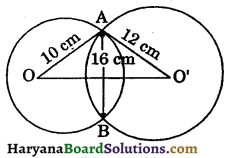
Solution:
Join OB and OB’.
In ΔAOO’ and ΔBOO’, we have
AO = BO [Each is 10 cm]
AO’ = BO’ [Each is 12 cm]
OO’ = OO (Common)
ΔAOO’ ≅ ΔBOO’
[By SSS congruence rule]

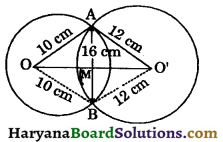
⇒ ∠AOO’ = ∠BOO’ [СРСТ]
⇒ ∠AOM = ∠BOM…..(i)
In ΔAOM and ΔBOM, we have
AO = BO [Each is 10 cm]
∠AOM = ∠BOM [As proved above in (i)]
OM = OM [Common]
ΔAOM ≅ ΔBOM [By SAS congruence rule]
⇒ ∠AMO = ∠BMO [CPCT]
But ∠AMO + ∠BMO = 180° [By linear pair axiom]
⇒ ∠AMO + ∠AMO = 180°
⇒ 2∠AMO = 180°
⇒ ∠AMO = \(\frac{180}{2}\) = 90°
∴ OM ⊥ AB
⇒ AM = BM = \(\frac{1}{2}\)AB
⇒ AM = BM = \(\frac{1}{2}\) × 16 = 8 cm
In right ΔAMO, we have ,
AO² = OM²+ AM² [By Pythagoras theorem]
⇒ 10² = OM² + 8²
⇒ 10² – 8² = OM²
⇒ (10 + 8)(10 – 8) = OM²
⇒ 18 × 2 = OM²
⇒ 36 = OM²
OM = \(\sqrt{36}=\sqrt{6 \times 6}\)
= 6 cm ……(ii)
In right ΔAO’M, we have
AO’ = O’M² + AM²
⇒ 12² = O’M² + 8²
⇒ 12² – 8² = O’M²
⇒ (12 + 8)(12 – 8) = O’M²
⇒ 20 × 4 = O’M²
⇒ 80 = O’M²
⇒ O’M = \(\sqrt{80}\)
⇒ O’M = \(\sqrt{4 \times 4 \times 5}=4 \sqrt{5}\) cm …..(iii)
⇒ OO’ = OM + O’M
⇒ OO’ = 6 + 4\(\sqrt{5}\) [using (ii) and (iii)]
Hence, distance between their centres is (6 + 4\(\sqrt{5}\)) cm.

Question 2.
AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q² = p² + 3r². [NCERT Exemplar Problems]
Solution:
We have
AB = 2AC ⇒ AC = \(\frac{1}{2}\)AB
Since, CM ⊥ AB and BN ⊥ AC
∴ OM ⊥ AB and ON ⊥ AC
⇒ BM = \(\frac{1}{2}\)AB and CN = \(\frac{1}{2}\)AC
In right ΔOMB, we have

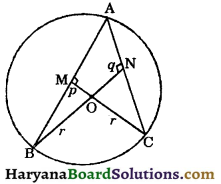
OB² = BM² + OM²
(By Pythagoras theorem)

In right ΔONC, we have
OC² = CN² + ON²
⇒ r² = \(\frac{r^2-p^2}{4}\) + q² [Using (i)]
⇒ 4r² = r² – p² + 4q²
⇒ 4r² – r² + p² = 4q²
⇒ p² + 3r² = 4q²
⇒ 4q² = p² + 3r². Hence proved

Question 3.
In the given figure, O is the centre of the circle, ∠BCO = 30°. Find the value of x and y. [NCERT Exemplar Problems]

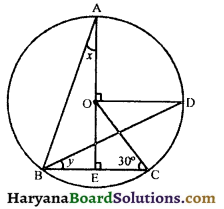
Solution:
∠AOD = ∠OEC = 90°
But these are corresponding angles
∴ OD || BC
⇒ ∠COD = ∠OCE (alternate interior angles)
⇒ ∠COD = 30° …….(i)
Arc CD subtends ∠COD at the centre and ∠CBD at the remaining part of the circle
∴ ∠COD = 2∠CBD
⇒ 30° = 2y [Using (i)]
⇒ y = \(\frac{30^{\circ}}{2}\) = 15°
Again arc AD substends ∠AOD at the centre and ∠ABD at the remaining part of the circle
∠AOD = 2∠ABD
⇒ 90° = 2∠ABD
⇒ ∠ABD = \(\frac{90}{2}\) = 46°
In triangle ABE, we have
∠AEC = ∠A + ∠B
⇒ 90° = x + ∠ABD + ∠DBC
⇒ 90° = x + 45° + y
⇒ 90° = x + 45° + 15°
⇒ 90° = x + 60°
⇒ x = 30° = 30°
Hence, x = 30° and y = 15°.

Question 4.
In the given figure, ABCD is a cyclic quadrilateral inscribed in a circle with centre O. CD is produced to E such that
∠ADE = 75°. If ∠ABO = 40°, find :
(i) ∠CAB (ii) ∠OAC.

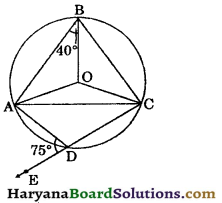
Solution:
∠ADE + ∠CDA = 180° (By linear pair axiom)
⇒ 75° + ∠CDA = 180°
⇒ ∠CDA = 180° – 75°
⇒ ∠CDA = 105°
Since, ABCD is a cyclic quadrilateral.
∴ ∠ABC + ∠CDA = 180°
[∵ Sum of opposite angles of a cyclic quadrilateral is 180°]
⇒ ∠ABC + 105° = 180°
⇒ ∠ABC = 180° – 105°
⇒ ∠ABC = 75°
AO = BO [Equal radii of same circle]
⇒ ∠OAB = ∠OBA
[Angles opposite to equal sides are equal]
⇒ ∠OAB = 40° ……(i)
Arc subtends ZAOC at the centre and ∠ABC at the remaining part of the circle.
∴ ∠AOC = 2∠ABC
⇒ ∠AOC = 2 × 75° [∵ ∠ABC = 75°]
⇒ ∠AOC = 150°
OA = OC
⇒ ∠OAC = ∠OCA
Let ∠OAC = ∠OCA = x°
In ΔAOC, we have
∠OAC + ∠OCA + ∠AOC = 180°
[∵ Sum of angles of a triangle is 180°]
⇒ x° + x° + 150° = 180
⇒ 2x° = 180° – 150°
⇒ 2x° = 30°
⇒ x° = \(\frac{30^{\circ}}{2}\) = 15°
⇒ ∠OAC = 15°
∠CAB = ∠OAC + ∠OAB
⇒ ∠CAB = 15° + 40°
⇒ ∠CAB = 55°
Hence, (i) ∠CAB = 55°, (ii) ∠OAC = 15°.

Question 5.
In the given figure, I is the incentre of ΔABC. AI when produced meets the circumcircle of ΔABC. If ∠ABC = 35° and ∠ACB = 70°, calculate :
(i) ∠IAB (ii) ∠DBC (iii) ∠BID.

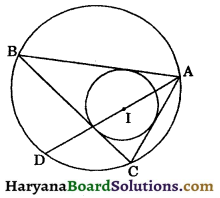
Solution:
Join BI and BD.
We know that, sum of angles of a triangle is 180°.
∴ In ΔABC, we have
∠ABC + ∠ACB + ∠BAC = 180°
⇒ 35° + 70° + ∠BAC = 180°
⇒ 105° + ∠BAC = 180°
⇒ ∠BAC = 180° – 105°
⇒ ∠BAC = 75°

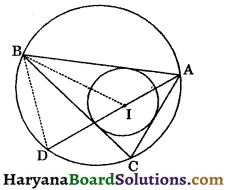
(i) ∵ AI is the bisector of ∠BAC.
∴ ∠BAD = ∠CAD = \(\frac{1}{2}\)∠BAC …(i)
⇒ ∠BAD = \(\frac{1}{2}\) × 75°
⇒ ∠IAB = 37.5° [∵ ∠BAD =∠IAB]
(ii) ∠CAD = \(\frac{1}{2}\)∠BAC [From (i)]
∠CAD = \(\frac{1}{2}\) × 75° = 37.5°
⇒ ∠DBC = ∠CAD [Angles in the same segment of a circle are equal]
⇒ ∠DBC = 37.5° …..(ii)
(iii) ∵ BI is the bisector of ∠ABC.
∴ ∠ABI = ∠CBI = \(\frac{1}{2}\)∠ABC
⇒ ∠CBI = \(\frac{1}{2}\) × 35°
⇒ ∠CBI = 17.5° ……(iii)
Adding (ii) and (iii), we get
∠DBC + ∠CBI = 37.5° + 17.5°
⇒ ∠DBI = 55°
∠ACB = ∠ADB [Angles in a same segment of a circle are equal]
⇒ 70° = ∠ADB
⇒ ∠ADB = 70°
⇒ ∠IDB = 70° ……(iv)
In ΔIBD, we have
∠DBI + ∠IDB + ∠BID = 180°
[Sum of angles of a triangles is 180°]
⇒ 55° + 70° + ∠BID = 180°
⇒ 125° + ∠BID = 180°
⇒ ∠BID = 180° – 125°
⇒ ∠BID = 55°
Hence, (i) ∠IAB = 37.5°
(ii) ∠DBC = 37.5°
(iii) ∠BID = 55°.

Question 6.
In the given the values, if \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\), then find the values of x, y and z.

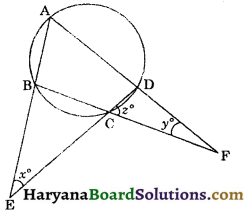
Solution:
Let \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\) = k
⇒ x = 2k, y = 3k, z = 5k …(i)
Since, ABCD is a cyclic quadrilateral.
∠A + ∠BCD= 180° …..(ii)
[Sum of opposite angles of cyclic quadrilateral is 180°]
∠BCD + ∠z = 180° …..(iii)
From (ii) and (iii), we get
∠A + ∠BCD = ∠BCD + ∠z
⇒ ∠A = ∠z …..(iv)
∠BCE = ∠z
(Vertically opposite angles) …(v)
In ΔBEC, we have
∠ABC = ∠BEC + ∠BCE [∵ Exterior angle is equal to sum of its two interior opp. angles]
⇒ ∠ABC = x° + z° …..(vi)
In ΔCDF, we have
∠ADC = ∠CFD + ∠DCF
[∵ Exterior angle is equal to sum of its two opposite interior angles]
⇒ ∠ADC = yo + zo …..(7)
But,∠ABC + ∠ADC = 180°
[∵ Sum of opposite angles of cyclic quadrilateral is 180°]
⇒ x° + z° + y° + z° = 180°[Using (vi) and (7)]
⇒ x° + y° + 2z° = 180°
⇒ 2k + 3k + 2 × 5k = 180°
⇒ 15k = 180°
⇒ k = \(\frac{180^{\circ}}{15}\) = 12°
∴ x = 2 × 12° = 24°,
y = 3 × 12° = 36°
and z = 5 × 12° = 60°
Hence, x = 24°, y = 36° and z = 60°.

Question 7.
Prove that the angle bisectors of the angles formed by producing opposite sides of cyclic quadrilateral (provided they are not parallel), intersect at right angles.
Solution:
Given : ABCD is cyclic quadrilateral in which opposite sides AD and BC when produced meet at P and opposite sides AB and DC when produced meet at Q. Bisectors of ∠APB and ∠AQD meet at point R.

To prove: ∠PRQ = ∠SRQ = 90°.
Construction : Since PR and QR are the bisectors of ∠APB and ∠AQD respectively.
∴ ∠1 = ∠2 and ∠3 = ∠4 …(i)
∠PDC = ∠ABC
[Exterior angle of a cyclic quadrilateral is equal to its opposite interior angle]
⇒ ∠PDM = ∠SBP …..(ii)
We know that sum of angles of a triangle is 180°.
In ΔPDM and ΔPBS, we have
∠PDM + ∠1 + ∠PMD = 180° …(iii)
∠SBP + ∠2 + ∠PSB = 180° …..(iv)
From (iii) and (iv), we get
∠PDM + ∠1 + ∠PMD = ∠SBP + ∠2 + ∠PSB
⇒ ∠PDM + ∠1 + ∠PMD = ∠PDM + ∠1 + ∠PSB
[Using (ii) and (i)]
⇒ ∠PMD = ∠PSB
⇒ ∠CMR = ∠RSQ
[∵ ∠CMR = ∠PMD (vertically oppoiste angles) and ∠PSB = ∠RSQ]
⇒ ∠QMR = ZRSQ ……(v)
In ΔQMR and ΔQSR, we have
∠3 = ∠4 [From (i)]
∠QMR = ∠RSQ [From (v)]
We know that if two angles of Ist triangle are equal to two angles of IInd triangle, then third angle of first triangle is also equal to the third angle of IInd triangle.
∴ ∠QRM = ∠QRS
But,∠QRM + ∠QRS = 180° (Linear pair axiom)
⇒ ∠QRM + ∠QRM = 180°
⇒ 2∠QRM = 180°
⇒ ∠QRM = \(\frac{180^{\circ}}{2}\) = 90°
⇒ ∠QRM = ∠QRS = 90°
Hence, ∠PRQ = ∠SRQ = 90°. Proved

Question 8.
D and E are respectively the points on equal sides AB and AC of an isosceles triangle ABC such that B, C, E and D are concyclic. If O is the point of intersection of CD and BE, prove that AO is the perpendicular bisector of line segment DE.
Solution:
In ΔABC, we have
AB = AC (given)
⇒ ∠B = ∠C ……(i)
[Angles opposite to equal sides are equal]
∠3 = ∠4 ……(ii)
[Angles in same segment of a circle are equal]

BCED is a cyclic quadrilateral.
∴ ∠B + ∠E = ∠C + ∠D= 180° [Sum of opposite angles of a cyclic quadrilateral is 180°]
⇒ ∠B + ∠E = ∠B + ∠D [Using (i)]
⇒ ∠D = ∠E ……(iii)
Subtracting (ii) from (iii), we get
∠D – ∠3 = ∠E – ∠4
⇒ ∠5 = ∠6
⇒ DO = EO …….(iv)
[Sides opposite to equal angles are equal]
From (iii), we have
∠D = ∠E
180° – ∠D = 180° – ∠E
⇒ ∠ADE = ∠AED
⇒ AD = AE ……(v)
In ΔADO and ΔAEO, we have
AD = AE [From (v)]
DO = EO [From (iv)]
AO = AO [Common]
∴ ΔADO ≅ ΔAEO (By SSS congruence rule)
⇒ ∠1 = ∠2 (CPCT)
In ΔAMD and ΔAME, we have
AD = AE [From (v)]
AM = AM [Common]
∠1 = ∠2 [As proved above]
∴ ΔAMD ≅ ΔAME
[By SAS congruence rule]
⇒ DM = ME (CPCT)
and ∠AMD = ∠AME (CPCT)
But, ∠AMD + ∠AME = 180° (By linear pair axiom)
⇒ ∠AMD + ∠AMD = 180°
⇒ 2∠AMD = 180°
⇒ ∠AMD = \(\frac{180^{\circ}}{2}\) = 90°
Hence, AO is the perpendicular bisector of line segment DE. Proved

Multiple Choice Questions

Choose the correct option in each of the following:

Question 1.
A circle divides a plane on which it lies into :
(a) 4 parts
(b) 2 parts
(c) 3 parts
(d) None of these
Answer:
(c) 3 parts

Question 2.
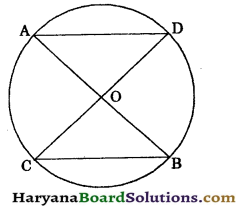
If the diagonals of a cyclic quadrilateral are the diameters of the circle through the vertices of a quadrilateral, then quadrilateral is a:
(a) square
(b) rectangle
(c) parallelogram
(d) rhombus
Answer:
(b) rectangle

Question 3.
Every cyclic parallelogram is a :
(a) rectangle
(b) square
(c) rhombus
(d) kite
Answer:
(a) rectangle

Question 4.
Angles in the same segment of a circle are :
(a) complementary
(b) supplementary
(c) equal
(d) unequal
Answer:
(c) equal

Question 5.
The length of a chord which is at a distance of 8 cm from the centre of a circle of radius 17 cm, is :
(a) 25 cm
(b) 30 cm
(c) 15 cm
(d) 20 cm
Answer:
(b) 30 cm

Question 6.
The region between a chord and either of it arcs is called :
(a) sector of a circle
(b) segment of a circle
(c) quadrant of a circle
(d) secant of a circle
Answer:
(b) segment of a circle

Question 7.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is : [NCERT Exemplar Problems]
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 12 cm
Answer:
(c) 10 cm

Question 8.
An equilateral triangle of side 9 cm is inscribed in a circle. The radius of the circle is :
(a) 2\(\sqrt{3}\) cm
(b) 3 cm
(c) 3\(\sqrt{3}\) cm
(d) \(\sqrt{3}\) cm
Answer:
(c) 3\(\sqrt{3}\) cm

Question 9.
In the given figure, AB and CD are two parallel chords such that BC is the diameter of the circle and AB = 6 cm, then length of CD is :

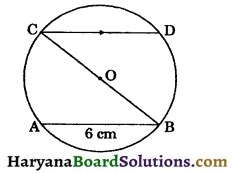
(a) 5 cm
(b) 9 cm
(c) 7 cm
(d) 6 cm
Answer:
(d) 6 cm

Question 10.
In the given figure, O is the centre of the circle, then length of AD is :

(a) 5 cm
(b) 4 cm
(c) 9 cm
(d) 3 cm
Answer:
(d) 3 cm

Question 11.
In the given figure, O is the centre of the circle. If OD ⊥ AC, OB = 5 cm, OD = 3 cm, then length of BD is :

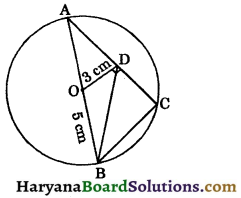
(a) 2\(\sqrt{13}\) cm
(b) 3\(\sqrt{13}\) cm
(c) 4\(\sqrt{13}\) cm
(d) \(\sqrt{51}\) cm
Answer:
(a) 2\(\sqrt{13}\) cm

Question 12.
In the given figure, O is the centre of a circle and A is point on the circle. If ∠OAB = 40°, then ∠ACB is equal to : [NCERT Exemplar Problems]

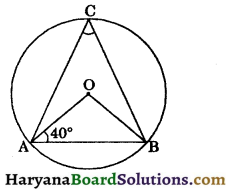
(a) 60°
(b) 40°
(c) 70°
(d) 50°
Answer:
(d) 50°