HBSE 8th Class Maths Solutions Chapter 8 राशियों की तुलना Ex 8.3

Haryana State Board HBSE 8th Class Maths Solutions Chapter 8 राशियों की तुलना Ex 8.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 8 राशियों की तुलना Ex 8.3

प्रश्न 1.
निम्नलिखित के लिए कुल राशि एवं चक्रवृद्धि ब्याज ज्ञात कीजिए –
(a) ₹ 10800 पर 3 वर्ष के लिए 12\(\frac{1}{2}\)% वार्षिक दर से वार्षिक रूप से संयोजित करने पर ।
(b) ₹ 18000 पर 2\(\frac{1}{2}\) वर्ष के लिए 10% वार्षिक दर से वार्षिक रूप से संयोजित करने पर ।
(c) ₹62500 पर 1\(\frac{1}{2}\) वर्ष के लिए 8% वार्षिक दर से अर्द्धवार्षिक रूप से संयोजित करने पर ।।
(d) ₹ 8000 पर 1 वर्ष के लिए 9% वार्षिक दर से अर्द्धवार्षिक रूप से संयोजित करने पर ।
(e) ₹ 10,000 पर 1 वर्ष के लिए 8% वार्षिक दर से अर्द्धवार्षिक रूप से संयोजित करने पर ।
हल :
(a) मुलधन, P = ₹0800
समय, n=3
दर, r = 12\(\frac{1}{2}\)% = \(\frac{25}{2}\)% वार्षिक
चक्रवृद्धि ब्याज = ?
चक्रवृद्धि मिश्रधन (कुल राशि), A = ?

हम जानते हैं कि,
या A = P(\(\left(1+\frac{r}{100}\right)^{n}\))
= 1080o(\(\left(1+\frac{25}{2×100}\right)^{3}\))
= 10800(\(\left(1+\frac{25}{200}\right)^{3}\))
A = 10800 × \((\frac{225}{200})^{3}\)
A = 10800\(\left(\frac{9}{8}\right)^{3}\)
= \(\frac{10800 \times 9 \times 9 \times 9}{8 \times 8 \times 8}\)
∴ A = \(\frac{492075}{32}\) = 15377.34
अतः मिश्रधन (कुल राशि) = 15377.34 रु.
चक्रवृद्धि ब्याज = मिश्रधन – मूलधन
= 15377.34 – 10800
∴ चक्रवृद्धि ब्याज = ₹4577.34

(b) हल : मूलधन, P =₹18000
समय, n = 2\(\frac{1}{2}\) वर्ष = (2+\(\frac{1}{2}\)) वर्ष
दर, r = 10%
चक्रवृद्धि मिश्रधन, A = ?
सर्वप्रथम 2 वर्ष का चक्रवृद्धि मिश्रधन निकालकर उस मिश्रधन को मूलधन मान कर वर्ष का साधारण ब्याज निकालेंगे ।
अत: चक्रवृद्धि मिश्रधन, A = 18000(\(\left(1+\frac{10}{100}\right)^{2}\))
= 18000 × (\(\left(\frac{11}{10}\right)^{2}\))
= 18000 × \(\frac{11}{10}\) × \(\frac{11}{10}\)
= \(\frac{180 \times 121}{1}\)
अतः, A = ₹ 21780
अब, मिश्रधन ₹ 21780 को मूलधन लेकर \(\frac{1}{2}\) वर्ष का साधारण ब्याज निकालेंगे ।

अत: साधारण ब्याज = = \(\frac{21780 \times 10 \times 1}{100 \times 2}\)
= ₹ 1089
∴ कुल धन = चक्रवृद्धि मिश्रधन + साधारण ब्याज
= 21780 + 1089
अत: मिश्रधन (कुल राशि) = ₹22869
चक्रवृद्धि ब्याज = 22869 – 18000 = 4869
∴ चक्रवृद्धि ब्याज = ₹4869

(c) हल : मूलधन, P= ₹ 62500
समय = \(\frac{3}{2}\) वर्ष = 3 अर्द्धवर्ष (व्याज अर्द्धवार्षिक)
दर, r = 8% वार्षिक
= \(\frac{8}{2}\) = 4% अर्द्धवार्षिक
मिश्रधन, कुल राशि A = ?
चक्रवृद्धि ब्याज, C.I. = ?
हम जानते है कि A = P\(\left(1+\frac{r}{100}\right)^{n}\)
= 62500\(\left(1+\frac{4}{100}\right)^{3}\)
= 62500\(\left(1+\frac{1}{25}\right)^{3}\)
= 62500\(\left(\frac{26}{25}\right)^{3}\)
= \(\frac{62500 \times 26 \times 26 \times 26}{25 \times 25 \times 25}\)
∴ मिश्रधन (कुल राशि) = 770304

चक्रवृद्धि ब्याज =A – P
= 70304 – 62500
अतः चक्रवृद्धि ब्याज = ₹7804

(d) हल : मूलधन, P = ₹ 8000
दर, r = 9% वार्षिक = 2% अर्द्धवार्षिक समय, n=1 वर्ष = 2 अर्द्धवर्ष
(∴ ब्याज छमाही है)

अतः मिश्रधन (कुल राशि) = ₹ 8736.20
चक्रवृद्धि ब्याज, C.I. = 8736.20 – 8000
∴ चक्रवृद्धि ब्याज = ₹736.20

(e) हल : मूलधन, P = ₹10,000
दर, r = 8% वार्षिक = \(\frac{8}{2}\)% = 4% अर्द्धवार्षिक
समय, n = 1 वर्ष = 2 अर्द्धवर्ष
(∴ ब्याज छमाही है)
मिश्रधन, A = ?
तथा चक्रवृद्धि ब्याज, CI = ?

अत:, मिश्रधन (कुल राशि) = 810816
चक्रवृद्धि ब्याज, C.I = A – P
= 10816 – 10000
= ₹ 816
अतः, चक्रवृद्धि ब्याज = ₹ 816

प्रश्न 2.
कमला ने एक स्कूटर खरीदने के लिए किसी बैंक से ₹26400 15% वार्षिक दर से उधार लिए, जबकि व्याज वार्षिक संयोजित होना है। 2 वर्ष 4 महीने के अन्त में ज्यार चुकता करने के लिए उसे कितनी राशि का भुगतान करना पड़ेगा?
हल :
मूलधन, P = ₹ 26400
दर, r = 15% वार्षिक
समय, n = 2\(\frac{4}{12}\) = 2\(\frac{1}{3}\) वर्ष
नोट : ब्याज को वार्षिक संयोजित करते हुए पहले 2 वर्ष के लिए मिश्रधन ज्ञात करेंगे तथा दूसरे वर्ष की कुल राशि पर \(\frac{4}{12}\) = \(\frac{1}{3}\) वर्ष का साधारण ब्याज ज्ञात करेंगे ।

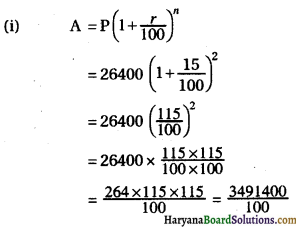
अत:, A = ₹ 34914

(ii) अब, हम ₹ 34914 पर 4 माह = \(\frac{1}{3}\) वर्ष का साधारण ब्याज ज्ञात करेंगे।

S.I = ₹ \(\frac{34914 \times 15 \times 1}{100 \times 3}\)
= \(\frac{34914}{20}\)
= latex]\frac{17457}{10}[/latex]
S.I = 81745.70
अतः कुल राशि = 34914 + 1745.70
= ₹ 36659.70
अत: कमला को उधार चुकता करने के लिए 36659.70 रु. का भुगतान बैंक को करना पड़ेगा।

प्रश्न 3.
फैबिना ने ₹ 12500 3 वर्ष के लिए 12% वार्षिक दर से साधारण ब्याज पर उधार लिए और राधा ने उतनी ही राशि उतने ही समय के लिए 10% वार्षिक दर से चक्रवृद्धि ब्याज पर उधार ली, जबकि व्याज वार्षिक रूप से संयोजित होना है। किसे अधिक व्याज का भुगतान करना है और कितना अधिक करना है?
हल :
फैबिना के लिए –
मूलधन, P = ₹12500
दर, r = 12% वार्षिक
समय, n = 3 वर्ष
साधारण ब्याज = \(\frac{12500 \times 12 \times 3}{100}\)
= ₹ 4500

राधा के लिए –
मूलधन, P = ₹ 12500
दर, r = 10% वार्षिक
समय, n=3 वर्ष
A = P\(\left(1+\frac{r}{100}\right)^{n}\)
= 12500\(\left(1+\frac{10}{100}\right)^{3}\)
= 12500 × \(\left(\frac{11}{10}\right)^{3}\)
= 12500 × \(\frac{11 \times 11 \times 11}{10 \times 10 \times 10}\)
∴ A = ₹ 16637.50
∴ चक्रवृद्धि ब्याज = 16637.50 – 12500
= ₹4137.50
अत: फैबिना को अधिक ब्याज का भुगतान करना होगा ।
वह अधिक भुगतान करती है = 4500 – 4137.50
= ₹ 362.50

प्रश्न 4.
मैंने जमशेद से ₹ 12000 2 वर्ष के लिए 6% वार्षिक दर से साधारण ब्याज पर उधार लिया । यदि मैंने यह राशि 6% वार्षिक दर से चक्रवृद्धि ब्याज पर उधार ली हुई होती तो मुझे कितनी अतिरिक्त राशि का भुगतान करना पड़ता ?
हल :
पहली स्थिति- मूलधन, P= ₹ 12000
दर, r = 6% वार्षिक
समय, n = 2 वर्ष

= \(\frac{12000 \times 6 \times 2}{100}\)
= ₹ 1440

अतः राशि, A₁ = मूलधन + ब्याज
= 12000 + 1440
= ₹ 13440

अत: राशि, A₁ = ₹ 13440.00

दूसरी स्थिति –
मूलधन, P = ₹ 12000
समय, n = 2 वर्ष
दर, r = 6% वार्षिक
A = ?

अत: मुझे अतिरिक्त राशि देनी पड़ती
= A₁ – A₂
= 13483.20 – 13440
= ₹ 43.20

प्रश्न 5.
वासुदेवन ने 12% वार्षिक दर पर ₹60,000 का निवेश किया । यदि व्याज अर्द्धवार्षिक संयोजित होता है तो ज्ञात कीजिए कि वह- (i) 6 माह के अन्त में (ii) 1 वर्ष के अन्त में, कुल कितनी राशि प्राप्त करेगा ?
हल :
(i) मूलधन, P = ₹60,000
दर, r = 12% वार्षिक = \(\frac{12}{2}\)% = 6% अर्द्धवार्षिक
समय, n = 6 माह = \(\frac{1}{2}\) वर्ष = 1 अर्द्धवर्ष
अत: A = P\(\left(1+\frac{r}{100}\right)^{n}\)
= 60,000\(\left(1+\frac{6}{100}\right)^{1}\)
= 60,000 × \(\frac{106}{100}\)
= 600 × 106
∴ मिश्रधन = ₹ 63,600

(ii) मूलधन, P = ₹ 60000
दर, r = \(\frac{12}{2}\) = 6% अर्द्धवार्षिक
समय, n = 1 वर्ष = 2 अर्द्धवर्ष

प्रश्न 6.
आरिफ ने एक बैंक से ₹ 80,000 का कर्ज लिया। यदि व्याज की दर 10% वार्षिक है तो 11 वर्ष पश्चात् उसके द्वारा भुगतान की जाने वाली राशियों में अन्तर ज्ञात कीजिए । यदि ब्याज (i) वार्षिक संयोजित होता है (ii) अर्द्धवार्षिक संयोजित होता है।
हल :
(i) मूलधन, P= ₹ 80,000
समय, n = 1\(\frac{1}{2}\) वर्ष = 1 वर्ष और 1 अर्द्धवर्ष
दर, r = 10% वार्षिक और 5% अर्द्धवार्षिक
कुल राशि A = P\(\left(1+\frac{r}{100}\right)^{n}\)
= 80,000(\(\left(1+\frac{10}{100}\right)^{1}\))(\(\left(1+\frac{5}{100}\right)^{1}\))
= 80,000(\(\frac{11}{10}\)) (\(\frac{21}{20}\))
= \(\frac{80000 \times 11 \times 21}{10 \times 20}\)
∴ A = ₹ 92400

(ii) मूलधन, P = ₹ 80000
दर, r = 10% = \(\frac{10}{2}\)% = 5% अर्द्धवार्षिक
समय, n = 1\(\frac{1}{2}\) वर्ष = \(\frac{3}{2}\)वर्ष या 3 अर्द्धवर्ष

भुगतान की जाने वाली राशियों में अन्तर
= ₹ (92610 – 92400)
= ₹ 210

प्रश्न 7.
मारिया ने किसी व्यापार में ₹ 8000 का निवेश किया । उसे 5% वार्षिक दर से चक्रवृद्धि ब्याज का भुगतान किया जायेगा । यदि व्याज वार्षिक रूप से संयोजित होता है, तो
(i) दो वर्ष के अन्त में उसके नाम से जमा की गई। राशि ज्ञात कीजिए । ,
(ii) तीसरे वर्ष का व्याज ज्ञात कीजिए ।
हल :
(i) मूलधन, P = ₹8000
दर, r = 5% वार्षिक
समय, n = 2 वर्ष
कुल राशि, A = P\(\left(1+\frac{r}{100}\right)^{n}\)
= 8,000(\(\left(1+\frac{5}{100}\right)^{2}\))
= 8,000(\(\left(\frac{21}{20}\right)^{2}\))
= 8,000 × \(\frac{21 \times 21}{20 \times 20}\)
= 20 × 21 × 21
कुल राशि, A = ₹ 8820

(ii) तीसरे वर्ष के व्याज के लिए
मूलधन, P = ₹8820
दर, =5% वार्षिक
समय. n = 1 वर्ष
साधारण व्याज = \(\frac{Prn}{100}\)
= \(\frac{8820 \times 5 \times 1}{100}\)
तीसरे वर्ष का व्याज = 441 रु.

प्रश्न 8.
₹ 10,000 रुपए पर 1\(\frac{1}{2}\) वर्ष के लिए 10% वार्षिक दर से चक्रवृद्धि ब्याज और कुल राशि ज्ञात कीजिए जबकि ब्याज अर्धवार्षिक संयोजित होना है। क्या यह ब्याज उस ब्याज से अधिक होगा जो उसे वार्षिक रूप से संयोजित करने पर प्राप्त होगा?
हल :
मूलधन, P= ₹ 10000
समय, n =1\(\frac{1}{2}\) वर्ष = \(\frac{3}{2}\) वर्ष = 3 अर्द्धवर्ष (ब्याज अर्द्धवार्षिक)
दर, r = 10% वार्षिक = \(\frac{10}{2}\) =5% अर्द्धवर्ष, A = ?

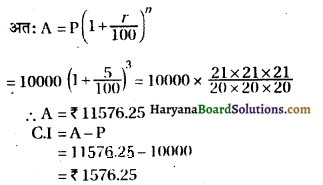
(ii) जब ब्याज वार्षिक संयोजित हो-
मूलधन, P= ₹1000
समय, n = 1 वर्ष और \(\frac{1}{2}\) वर्ष या 1 वर्ष और 1 अर्द्धवर्ष
दर, r = 10%, वार्षिक और 5%, अर्द्धवार्षिक

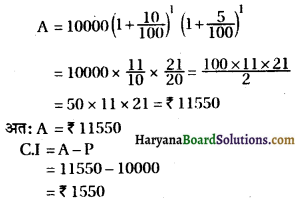
हाँ, अर्द्धवार्षिक ब्याज, उस ब्याज से अधिक होगा जो उसे वार्षिक रूप से संयोजित करने पर प्राप्त होगा।

प्रश्न 9.
यदि राम ₹4096 18 महीने के लिए 12\(\frac{1}{2}\)% वार्षिक दर पर उधार देता है और ब्याज अर्द्धवार्षिक संयोजित होता है तो ज्ञात कीजिए कि राम कुल कितनी राशि प्राप्त करेगा?
हल :
मूलधन, P = ₹ 4096
दर, r = 12\(\frac{1}{2}\) %, वार्षिक = \(\frac{25}{2}\)% वार्षिक
= \(\frac{25}{4}\)% अर्द्धवार्षिक
समय, n = 18 महीने = 1\(\frac{1}{2}\) वर्ष = \(\frac{3}{2}\) = 3 अर्द्धवर्ष
A = ?

प्रश्न 10.
5% वार्षिक दर से बढ़ते हुए वर्ष 2003 के अन्त में एक स्थान की जनसंख्या 54000 हो गई। निम्नलिखित को ज्ञात कीजिए
(i) वर्ष 2001 में जनसंख्या,
(ii) वर्ष 2005 में कितनी जनसंख्या होगी ?
हल :
(i) प्रत्येक वर्ष जनसंख्या बढ़ने की दर,
r = 5% वार्षिक
समय n = 2 वर्ष
2003 में जनसंख्या , A = 54000
माना कि वर्ष 2001 में जनसंख्या थी, P = x

(ii) 2 वर्ष बाद 2005 में जनसंख्या –

प्रश्न 11.
एक प्रयोगशाला में, किसी निश्चित प्रयोग में बैक्टीरिया की संख्या 2.5% प्रति घंटे की दर से बढ़ रही है। यदि प्रयोग के शुरू में बैक्टीरिया की संख्या 506000 थी तो 2 घंटे के अन्त में बैक्टीरिया की संख्या ज्ञात कीजिए।
हल:
दर, r = 2.5% प्रति घंटे
समय, n = 2 घंटे
शुरू में बैक्टीरिया की संख्या P (माना) = 506000
अत: 2 घंटे बाद वैक्टीरिया की संख्या, माना A है।

प्रश्न 12.
एक स्कूटर ₹42000 में खरीदा गया । 8% वार्षिक दर से इसके मूल का अवमूल्यन हो गया । 1 वर्ष बाद स्कूटर का मूल्य ज्ञात कीजिए।
हल:
स्कूटर का मूल्य = ₹ 42000
1 वर्ष बाद मूल्य में कमी = 42000 का 8%
= 42000 × \(\frac{8}{100}\)
= ₹ 420 × 8
= ₹3360
1 वर्ष बाद स्कूटर का मूल्य = 42000 – 3360
= ₹38640