HBSE 8th Class Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.3

Haryana State Board HBSE 8th Class Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.3

Question 1.
निम्नलिखित संख्याओं के वर्गमूल ज्ञात करने में .इकाई अंक की क्या संभावना है-
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
हल:
(i) 9801 – चूंकि 9801 में इकाई का अंक 1 है, अत: इसके वर्गमूल का इकाई अंक 1 या 9 हो सकता है।

(ii) 99856 – चूंकि इस संख्या में इकाई का अंक 6 है, अत: इसके वर्गमूल का इकाई अंक 4 . या 6 हो सकता है।

(iii) 998001 – चूंकि इसमें इकाई का अंक 1 है, अत: इसके वर्गमूल का इकाई अंक 1 या 9 हो सकता है।

(iv) 657666025 – चूँकि इस संख्या का इकाई का अंक 5 है, अत: इसके वर्गमूल का इकाई का अंक भी 5 होगा ।

प्रश्न 2.
बिना गणना किये वह संख्या बताएं जो वास्तव में पूर्ण वर्ग नहीं है –
(i) 153 (ii) 257 (iii) 408 (iv) 441
हल :
नियम: जिन संख्याओं में इकाई के अंक 2,3,7 या 8 होते हैं, वे संख्याएँ कभी पूर्ण वर्ग संख्या नहीं होती हैं ।
(i) 153 – चूँकि इस संख्या में इकाई का अंक 3 है ।
अतः 153 पूर्ण वर्ग नहीं है ।

(ii) 257 – चूँकि इस संख्या में इकाई का अंक 7 है।
अत: 257 पूर्ण वर्ग नहीं है ।

(iii) 408 – चूँकि इस संख्या में इकाई का अंक 8 है।
अत: 408 पूर्ण वर्ग नहीं है।

(iv) 441 – चूँकि इस संख्या में इकाई का अंक 1 है ।
अत: 441 पूर्ण वर्ग हो सकती है ।

प्रश्न 3.
बार-बार घटाने की विधि से 100 तथा 169 का वर्गमूल ज्ञात कीजिए।
हल:
(a) 100 – 1 = 99
(b) 99 – 3 = 96
(c) 96 – 5 = 91
(d) 91 – 7 = 84
(e) 84 – 9 = 75
(f) 75 – 11 = 64
(g) 64 – 13 = 51
(h) 51 – 15 = 36
(i) 36 – 17 = 19
(j) 19 – 19 = 0
चूँकि संख्या 1 से क्रमागत विषम संख्याओं को 100 में से घटाने पर 10 वाँ पद (0) शून्य प्राप्त होता है ।
अत: \(\sqrt {100}\) = 10

(ii) 169
(a) 169 – 1 = 168
(b) 168 – 3 = 165
(c) 165 – 5 = 160
(d) 160 – 7 = 153
(e) 153 – 9= 144
(f) 144 – 11 = 133
(g) 133 – 13 = 120
(h) 120 – 15 = 105
(i) 105 – 17= 88
(j) 88 – 19 = 69
(k) 69 – 21 = 48
(l) 48 – 23 = 25
(m) 25 – 25 = 0
चूँकि संख्या 1 से क्रमागत विषम संख्याओं को 169 में से घटाने पर 13 वाँ पद 0 शून्य प्राप्त होता है ।
अत: \(\sqrt {169}\) = 13

प्रश्न 4.
अभाज्य गुणनखण्ड विधि से निम्नांकित संख्याओं का वर्गमूल ज्ञात कीजिए –
(i) 729
(ii) 400
(ii) 1764
(iv) 4096
(v) 7744
(vi) 9604
(vii) 5929
(viii) 9216
(ix) 529
(x) 8100
हल:
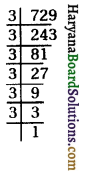
(i) 729
729 = 3 × 3 × 3 × 3 × 3 × 3
= 3² × 3² × 3²
= (3 × 3 × 3)²
= (27)²
अत: \(\sqrt {729}\) = 27

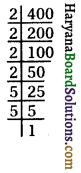
(ii) 400
400 = 2 × 2 × 2 × 2 × 5 × 5
= 2² × 2² × 5²
= (2 × 2 × 5)²
= (20)²
अत: \(\sqrt {200}\) = 20

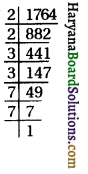
(iii) 1764
1764 = 2 × 2 × 3 × 3 × 7 × 7
= 2² × 3² × 7²
= (2 × 3 × 7)²
= (42)²
अत: \(\sqrt {1764}\) = 42

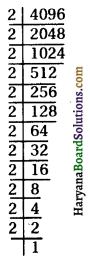
(iv) 4096
4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2² × 2² × 2² × 2² × 2² × 2²
= (2 × 2 × 2 × 2 × 2 × 2)²
= (64)²
अत: \(\sqrt {4096}\) = 64

प्रश्न 5.
निम्नलिखित संख्याओं में प्रत्येक के लिए वह सबसे छोटी पूर्ण संख्या ज्ञात कीजिए, जिससे इस संख्या को गुणा करने पर यह एक पूर्ण वर्ग संख्या बन जाये । इस पूर्ण वर्ग संख्या का वर्गमूल ज्ञात कीजिए
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768
हल :
(i) 252
252 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 7

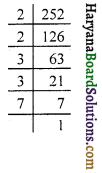
अभाज्य गुणनखण्ड के अनुसार 7 का जोड़ा नहीं है।
अत: यदि 7 का एक जोड़ा बनाते हैं तब संख्या 252 पूर्ण वर्ग हो जायेगी ।
अत: 252 में 7 का गुणा करने पर-
252 × 7 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{7 \times 7}\)
= 1764 एक पूर्ण वर्ग संख्या है।
अत: सबसे छोटी वांछित संख्या = 7
और \(\sqrt {1764}\) = 2 × 3 × 7
= 42.

(ii) 180
180 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 5

अभाज्य गुणनखण्ड के अनुसार 5 का जोड़ा नहीं है।
अत: 180 में 5 का गुणा करने पर-
180 × 5 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\)
= 900 (पूर्ण वर्ग संख्या )
अत: सबसे छोटी वांछित संख्या = 5
और \(\sqrt {900}\) = 2 × 3 × 5
= 30.

(iii) 1008
1008 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 7.

अभाज्य गुणनखण्ड के अनुसार 7 का जोड़ा नहीं है।
अत: 1008 में 7 का गुणा करने पर-
1008 × 7 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{7 \times 7}\)
= 7056 (पूर्ण वर्ग संख्या)
अत: सबसे छोटी वांछित संख्या = 7
तथा \(\sqrt {7056}\) = 2 × 2 × 3 × 7 = 84.

(iv) 2028
2028 = \(\underline{2 \times 2}\) × \(\underline{13 \times 13}\) × 3

अभाज्य गुणनखण्ड के अनुसार 3 का जोड़ा नहीं है।
अत: 2028 में 3 का गुणा करने पर-
2028 × 3 =\(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{13 \times 13}\) (पूर्ण वर्ग संख्या)
= 6084
अत: सबसे छोटी वांछित संख्या = 3
और ∴ \(\sqrt {6084}\) = 2 × 3 × 13 = 78

(v) 1458
1458 = \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × 2

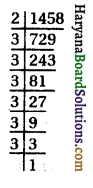
अभाज्य गुणनखण्ड के अनुसार 2 का जोड़ा नहीं है।
अत: 1458 में 3 का गुणा करने पर-
1458 × 2 = \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × \(\underline{2 \times 2}\) (पूर्ण वर्ग संख्या)
अत: सबसे छोटी वांछित संख्या = 2
अत: \(\sqrt {2916}\) = 2 × 3 × 3 × 3 = 54

(vi) 768
768 = 2 × 2 × 2 × 2 ×2 × 2 × 2 × 2 × 3

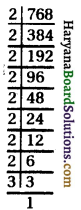
अभाज्य गुणनखण्ड के अनुसार 3 का जोड़ा नहीं है।
अत: 768 में 3 का गुणा करने पर-
768 × 3 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\)
अत: सबसे छोटी वांछित संख्या = 3
\(\sqrt {2304}\) = 2 × 2 × 2 × 2 × 3 = 48.

प्रश्न 6.
निम्नलिखित संख्याओं में प्रत्येक के लिए वह सबसे छोटी पूर्ण संख्या ज्ञात कीजिए जिससे इस संख्या को भाग देने पर वह एक पूर्ण वर्ग संख्या बन जाए। इस तरह ज्ञात की गई संख्या का वर्गमूल भी ज्ञात कीजिए।
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620
हल:
(i) 252
252 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 7

अभाज्य गुणनखण्ड के अनुसार 7 का जोड़ा नहीं है।
इसलिए, 252 में 7 का भाग दिया जाय, तो
252 ÷ 7 = 36
= \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\)
अत: सबसे छोटी वांछित संख्या = 7
और \(\sqrt {36}\) = 6

(ii) 2925
2925 = \(\underline{5 \times 5}\) × \(\underline{3 \times 3}\) × 13

अभाज्य गुणनखण्ड के अनुसार 13 का जोड़ा नहीं है।
इसलिए, 2925 में 13 का भाग दिया जाय, तो
2925 ÷ 13 = 225
= \(\underline{5 \times 5}\) × \(\underline{3 \times 3}\)
अत: सबसे छोटी वांछित संख्या = 13 और
\(\sqrt {225}\) = 15

(iii) 396
396 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 11

अभाज्य गुणनखण्ड के अनुसार 11 का जोड़ा नहीं है।
अत: 396 में 11 का भाग देने पर-
396 ÷ 11 = 36 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\)
अत: सबसे छोटी वांछित संख्या = 11
और \(\sqrt {36}\) = 2 × 3 = 6

(iv) 2645
2645 = \(\underline{23 \times 23}\) × 5

अभाज्य गुणनखण्ड के अनुसार 5 का जोड़ा नहीं है।
अत: 2645 में 5 का भाग देने पर-
2645 ÷ 5 = 529 = 23 × 23
अत: सबसे छोटी संख्या = 5
और \(\sqrt {529}\) = 23.

(iv) 2800
2800 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{5 \times 5}\) × 7

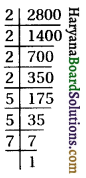
अभाज्य गुणनखण्ड के अनुसार 7 का जोड़ा नहीं है।
अत: 2800 में 7 का भाग देने पर-
2800 ÷ 7 = 400 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{5 \times 5}\)
अत: सबसे छोटी संख्या = 7
और \(\sqrt {400}\) = 2 × 2 × 5 = 20

(iv) 1620
1620 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × 5

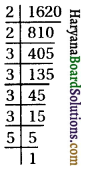
अभाज्य गुणनखण्ड के अनुसार 5 का जोड़ा नहीं है।
अत: 1620 में 5 का भाग देने पर-
1620 ÷ 5 = 324 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\)
अत: सबसे छोटी संख्या = 5
और \(\sqrt {324}\) = 2 × 2 × 3
\(\sqrt {324}\) = 18

प्रश्न 7.
एक राष्ट्रीय विद्यालय में कक्षा VIII के सभी विद्यार्थियों ने प्रधानमंत्री राहत कोष में 2401 रुपए दान में दिए। प्रत्येक विद्यार्थी ने उतने ही रुपए दान में दिए जितने कक्षा में विद्यार्थी थे। कक्षा के विद्यार्थियों की संख्या ज्ञात कीजिए।
हल:
माना, विद्यार्थियों में कुल संख्या = x
प्रत्येक विद्यार्थी ने दान में दिए = ₹ x

अतः x × x = 2401 (∵ कुल दान में रु. दिये)
x² = 2401
x = \(\sqrt{2401}\)
= \(\sqrt{7 \times 7 \times 7 \times 7}\)
x = 7 × 7 = 46
अत: कक्षा में कुल विद्यार्थियों की संख्या = 49

प्रश्न 8.
एक बाग में 2025 पौधे इस प्रकार लगाये जाने हैं कि प्रत्येक पंक्ति में उतने ही पौधे हों, जितनी पंक्तियों की संख्या हो । पंक्तियों की संख्या और प्रत्येक पंक्ति में पौधों की संख्या ज्ञात कीजिए।
हल:
माना, पंक्तियों की संख्या = x
तथा प्रत्येक पंक्ति में पौधों की संख्या =x

∴ कुल पौधों की संख्या= x × x = 2025
∴ x² = 2025
x = \(\sqrt{2025}\) = \(\sqrt{3 \times 3 \times 3 \times 3 \times 5 \times 5}\)
∴ x = 5 × 3 × 3 = 45
अतः पंक्तियों की संख्या = 45 तथा
प्रत्येक पंक्ति में पौधे की संख्या = 45

प्रश्न 9.
वह सबसे छोटी वर्ग संख्या ज्ञात कीजिए जो 4, 9 और 10 प्रत्येक से विभाजित हो जाए।
हल:
4,9 व 10 का ल. स. प.
= 2 × 2 × 3 × 3 × 5
= 180

180 का अभाज्य गुणनखण्ड = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 5
इस गुणनखण्ड में 5 का जोड़ा नहीं है।
∴ 180 पूर्ण वर्ग संख्या नहीं है।
अतः 180 को पूर्ण वर्ग संख्या बनाने के लिए 5 का गुणा किया जाये, जिससे 180 के गुणनखण्ड में 5 का जोड़ा बन जायेगा ।
∴ 180 × 5 = 900 (यह पूर्ण वर्ग संख्या है)
= \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\)
अत: अभीष्ट सबसे छोटी वर्ग सख्या = 900

प्रश्न 10.
वह सबसे छोटी वर्ग संख्या ज्ञात कीजिए, जो प्रत्येक 8, 15 और 20 से विभाजित हो जाये।
हल :
8, 15 व 20 का ल. स. प.
= 2 × 2 × 2 × 3 × 5
= 120

अत: इनके जोड़ा बनाने के लिए 120 में 2,3 व 5 का गुणा करना पड़ेगा।
अत: संख्या = 120 × 2 × 3 × 5
= 3600 ⇒ \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\)
अत: पूर्ण वर्ग संख्या = 3600
जो कि, क्रमशः प्रत्येक 8, 15, 20 से पूर्णतः विभाजित भी होगी ।
अभीष्ट सबसे छोटी वर्ग संख्या = 3600