Haryana State Board HBSE 12th Class Physics Solutions Chapter 7 Alternating Current Textbook Exercise Questions and Answers.
Haryana Board 12th Class Physics Solutions Chapter 7 Alternating Current
प्रश्न 7.1.
एक 100 52 का प्रतिरोधक 220 V 50Hz आपूर्ति से संयोजित है।
(a) परिपथ में धारा का rms मान कितना है?
(b) एक पूरे चक्र में कितनी नेट शक्ति व्यय होती है?
उत्तर:
हल दिया गया है-
R = 10052
Erms = 220 V
आवृत्ति f = 50 Hz
(a) परिपथ में धारा का mms मान होगा
Irms = \(\frac{E_{\text {mws }}}{R}\)
= \(\frac{220}{100}\) = 2. 2A
(b) शक्ति व्यय (P) हुई = ?
P= Irms × Erms
= 2.2 x 220
= 484 W प्रति चक्र
प्रश्न 7.2.
(a) ac आपूर्ति का शिखर मान 300v है। rms वोल्टता कितनी है?
(b) ac परिपथ में धारा का rms मान 10 A है शिखर धारा कितनी है?
उत्तर:
हल दिया गया है- E0 = 300 V
Erms = ?
Irms= 10 A
I0 = ?
(a) हम जानते हैं – Erms = \(\frac{E_0}{\sqrt{2}}\)
= 0.707 × 300
= 212.100
= 212.1 V प्राप्त करते हैं।
(b) Irms = \(\frac{\mathrm{I}_0}{\sqrt{2}}\)
∴ I0 = \(\sqrt{2} I_{\mathrm{rms}}\)
= √2 × 10
= 1.414 × 10 = 14.14 A
![]()
प्रश्न 7.3.
एक 44 mH की प्रेरक कुण्डली को 220 V, 50 परिपथ में धारा के rms मान को ज्ञात कीजिए।
उत्तर:
हल दिया गया है-
L = 44 mH = 44 x 10-3 H
Erms = 220 V
f = 50 Hz
Irms = ?
XL = Lω
= L × 2πf
XL = 44 × 10-3 × 2 × \(\frac{22}{7}\) × 50Ω

प्रश्न 7.4.
एक 60 µF का संधारित्र 110 V, 60 Hz ac आपूर्ति से जोड़ा गया है। परिपथ में धारा के rms मान को ज्ञात कीजिए।
उत्तर:
हल दिया गया है-
C = 60 µF = 60 × 10-6 F
Erms = 110 V
f = 60 Hz
Irms = ?
\(I_{\mathrm{rms}}=\frac{\mathrm{E}_{\mathrm{rms}}}{X_{\mathrm{C}}}=\omega C \mathrm{E}_{\mathrm{rms}}\)
Irms = 2πfC Erms
= 2 × 3.14 × 60 x 60 x 10 x 110
= 2.49 A
प्रश्न 7.5
प्रश्न 7.3 व 7.4 में एक पूरे चक्र की अवधि में प्रत्येक परिपथ में कितनी नेट शक्ति अवशोषित होती है? अपने उत्तर का विवरण दीजिए।
उत्तर:
हल – संधारित्र एवं प्रेरण कुण्डली के लिये वोल्टता और धारा के
मध्य कलान्तर Φ = ± \(\frac{\pi}{2}\) अतः एक पूरे चक्र में शक्ति व्यय
P = Erms Irms cos Φ
P = Erms Irms cos \(\left( \pm \frac{\pi}{2}\right)\) = 0
यहाँ पर Φ = \(\frac{\pi}{2}\)
∴ cos Φ = cos \(\frac{\pi}{2}\) = 0
∴ Pav = 0 प्रत्येक स्थिति के लिए
![]()
प्रश्न 7.6.
एक LCR परिपथ की, जिसमें L=2.0 H, C = 32 µF तथा R = 10 Ω अनुनाद आवृत्ति ωr परिकलित कीजिए। इस परिपथ के लिए Q का क्या मान है?
उत्तर:
हल-दिया गया है-
L = 2.0 H
C = 32 µF = 32 × 10-6F
तथा R = 10 Ω
अनुनाद आवृत्ति ωr = ?
इस परिपथ के लिए आवेश = Q = ?

प्रश्न 7.7.
30 µF का एक आवेशित संधारित्र 27 mH की प्रेरण कुण्डली से जोड़ा गया है। परिपथ के मुक्त दोलनों की कोणीय आवृत्ति कितनी है?
उत्तर:
हल-दिया गया है-
c = 30 µF = 30 × 10-6F
L = 27 mH = 27 × 10-3 H
हम जानते हैं-

प्रश्न 7.8.
कल्पना कीजिए कि अभ्यास 7.7 में संधारित्र पर प्रारम्भिक आवेश 6 mC है। प्रारम्भ में परिपथ में कुल कितनी ऊर्जा संचित होगी? बाद में कुल ऊर्जा कितनी होगी?
उत्तर:
हल-दिया गया है-
q = 6 mC = 6 × 10-3C
C = 30 µF = 30 × 10-6F
फुल ऊर्जा संचित UE = ?
अतः प्रारम्भ में संचित ऊर्जा UE = [/latex]\frac{\mathrm{q}^2}{2 \mathrm{C}}[/latex]
मान रखने पर UE = \(\frac{1}{2}\left(\frac{\left(6 \times 10^{-3}\right)^2}{30 \times 10^{-6}}\right)\)
= \(\frac{36}{2 \times 30}=\frac{6}{10}\)
UE = 0.6 J
यदि हम परिपथ में ऊर्जा हास को शून्य मानें तो यह ऊर्जा बाद में प्रेरकत्व एवं संधारित्र में संचित ऊर्जाओं में विभक्त हो जायेगी, जिसका कुल मान एक समान रहेगा अर्थात् 0.6 जूल ही रहेगा।
प्रश्न 7.9.
एक श्रेणीबद्ध LCR परिपथ को, जिसमें R = 20 Ω, L=1.5 H तथा C = 35 µF, एक परिवर्ती आवृत्ति की 200 V ac आपूर्ति से जोड़ा गया है। जब आपूर्ति की आवृत्ति परिपथ की मूल आवृत्ति के बराबर होती है, तो एक पूरे चक्र में परिपथ को सथानान्तरित की गई माध्य शक्ति कितनी होगी?
उत्तर:
हल-दिया गया है
R = 20 Ω,
L = 1.5 H
C = 35 µF = 35 × 10-6 F
Erms = 200 V
आवृत्ति f = परिवर्ती
जब आपूर्ति की आवृत्ति परिपथ की प्राकृतिक आवृत्ति के बराबर होती है तब अनुनाद होता है और उस स्थिति में XL =XC इस स्थिति में Z= R = 20 ओम होगा और Φ = 0°
चूँकि Z = \(\sqrt{R^2+\left(X_L-X_C\right)^2}\) होता है।
Ir.m.s = \(\frac{E_{\text {sms }}}{Z}=\frac{200}{20}\) = 10 A
एक पूरे चक्र में शक्ति स्थानान्तरित की गई है
= Erms × Irms
P = 200 V × 10 A
= 2000 W = 2 kW
![]()
प्रश्न 7.10.
एक रेडियो को MW प्रसारण बैंड के एक खण्ड के आवृत्ति परास के एक ओर से दूसरी ओर (800 kHz से 1200 kHz) तक समस्वरित किया जा सकता है। यदि इसके LC परिपथ का प्रभावकारी प्रेरकत्व 200 µH हो, तो उसके परिवर्ती संधारित्र की परास कितनी होनी चाहिए? (संकेत-समस्वरित करने के लिए मूल आवृत्ति अर्थात् LC परिपथ के मुक्त दोलनों की आवृत्ति रेडियो तरंग की आवृत्ति के समान होनी चाहिए।)
उत्तर:
हल-दिया गया है-
आवृत्ति f1 = 800 kHz
= 8 × 10-5
आवृत्ति f2 = 1200 kz
= 12 × 105 Hz
L = 200 μH = 200 × 10-6H
= 2 × 10-4H, C = ?
हम जानते हैं कि अनुनाद की आवृत्ति

प्रश्न 7.11.
चित्र में एक श्रेणीबद्ध LCR परिपथ दिखाया गया है जिसे परिवर्ती आवृत्ति के 230 V के स्रोत से जोड़ा गया है। L = 5.0 H, C = 80 μF, R = 40 Ω
(a) ख्रोत की आवृत्ति निकालिए जो परिफ्थ में अनुनाद उत्पन्न करे।
(b) परिपथ की प्रतिबाधा ε तथा अनुनादी आवृत्ति पर धारा का आयाम निकालिए।
(c) परिपथ के तीनों चित्र अवयवों के सिरों पर विभवपात के rms मानों को निकालिए। दिखलाइए कि अनुनादी आवृत्ति पर LC संयोग के सिरों पर विभवपात शन्य है।
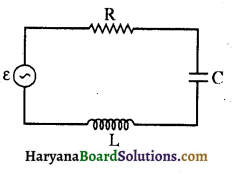
उत्तर:
हल-दिया गया है L = 50. H
C = 80 μF = 80 × 10-6F
R = 40 Ω
Erms = 230 V
(a) स्रोत की आवृत्ति f जो परिपथ में अनुनाद fr उत्पन्न करे

(b) माना अनुनाद पर परिपथ प्रतिबाधा Z है और Im धारा का आयाम = धारा का शीर्षमान तब

∴ I0 = Irms√2
= 5.75 × √2A
= 8. 13 A = 8.1 A
(c) प्रतिरोध के सिरों पर विभवपात का मान होगा
VR = Irms R
= 5. 75 × 50 × 5.0
Vrms 1437.5 V
इसी तरह से C के सिरों पर विभवपात का मान निकालने पर
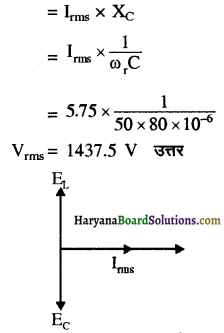
C के सिरों पर विभवपात = L के सिरों पर विभवपात EL, EC के बराबर व विपरीत है। अतः अनुनादी आवृत्ति पर LC संयोग के सिरों पर विभवान्तर का मान शून्य होता है।
अतिरिक्त अभ्यास प्रश्न (NCERT)
प्रश्न 7.12
किसी LC परिपथ में 20 mH का एक प्रेरक तथा 50 μF का एक संधारित्र है जिस पर प्रारम्भिक आवेश 10 mC है। परिपथ का प्रतिरोध नगण्य है। मान लीजिए कि वह क्षण जिस पर परिपथ बन्द किया जाता है t = 0 है।
(a) प्रारम्भ में कुल कितनी ऊर्जा संचित है? क्या यह LC दोलनों की अवधि में संरक्षित है?
(b) परिपथ की मूल आवृत्ति क्या है?
(c) किस समय पर संचित ऊर्जा
(i) पूरी तरह से वैद्युत है (अर्थात् वह संधारित्र में संचित है?
(ii) पूरी तरह से चुंबकीय है (अर्थात् प्रेरक में संचित है?
(d) किन समयों पर सम्पूर्ण ऊर्जा प्रेरक एवं संधारित्र के मध्य समान रूप से विभाजित है?
(e) यदि एक प्रतिरोधक को परिपथ में लगाया जाए तो कितनी ऊर्जा अंततः ऊष्मा के रूप में क्षयित होगी?
उत्तर:
हल-दिया गया है
L = 20 mH = 20 × 10-3 H
C = 50 μF = 50 × 10-6 F
q0 = 10 mC = 10 × 10-3 C
t = 0 पर q = q0
q0 = 10 × 10-3 C (प्रारम्भिक आवेश है)
तथा q = q0 cos ωt
(a) प्रारम्भ में कुल ऊर्जा का मान

हाँ L तथा C में संचित ऊर्जाओं का योग संरक्षित है यदि R = 0

(c) किसी भी क्षण, धारित्र पर आवेश
q = q0 cos ωt
= q0 cos \(\left(\frac{2 \pi}{T} \cdot t\right)\) से व्यक्त किया जाता है।
(i) t = 0, \(\frac{\Gamma}{2}\), T, \(\frac{3 \mathrm{~T}}{2}\) समयों पर
q = q0 (आरम्भ में दत्त अधिकतम आवेश)
∴ ऊर्जा धारित्र में संचित होती है। अतः यह पूर्णरूपेण वैद्युत ऊर्जा है क्योंकि इसका अधिकतम मान इन्हीं समयों पर होता है जहाँ
T = \(\frac{1}{\mathrm{f}}\) = 6. 28 × 10-3 s
= 6. 28 ms
(ii) L में संचित ऊर्जा उस समय अधिकतम होगी जब C में वैद्युत ऊर्जा शून्य होगी।
अर्थात् q = 0
q उस समय शून्य होगा जब
cos ωt = cos \(\frac{\pi}{2}\) = 0
∴ t = \(\frac{T}{4}, \frac{3 \mathrm{~T}}{4}, \frac{5 \mathrm{~T}}{4}\) ……………… आदि समय पर q शून्य है।
अतः संचित ऊर्जा पूर्णरूपेण चुम्बकीय ऊर्जा है।

(e) यदि एक प्रतिरोधक को परिपथ में लगाया जाये तो LC दोलनों को अवमंदित कर देता है। उनका आयाम कम हो जाता है और अन्त में मर जाते हैं। इस स्तर पर कुल प्रारम्भिक ऊर्जा = 1.0 J ऊष्मा के रूप में क्षयित हो जाती है।
![]()
प्रश्न 7.13.
एक कुण्डली को जिसका प्रेरण 0.50 H तथा प्रतिरोध 100 Ω है, 240 V व 50 Hz की एक आपूर्ति से जोड़ा गया है।
(a) कुण्डली में अधिकतम धारा कितनी है?
(b) वोल्टेज शीर्ष व धारा शीर्ष के बीच समय-पश्चता (time lag) कितनी है?
उत्तर:
हल-दिया गया है-
L = 0.50 H
R = 100 Ω
a.c. आपूर्ति की आवृत्ति f = 50 Hz
a.c. आपूर्ति का rms का मान = Erms = 240 V
∴ कोणीय आवृत्ति = ω = 2πf
= 2π × 50
= 100 π rad s-1
और E0 = √2Erms
= √2 × 240 V
(a) कुण्डली में अधिकतम धारा = I0 = ?

(b) LR परिपथ के लिए
यदि E = E0 cos ωt
तब I = I0 cos ( ωt – Φ)
स्पष्ट है कि E अधिकतम t = 0 पर होगा और I अधिकतम ωt = Φ पर होगा

प्रश्न 7.14.
यदि परिपथ को उच्च आवृत्ति की आपूर्ति ( 240 V, 10 kHz ) से जोड़ा जाता है तो अभ्यास 7.13 (a) तथा (b) के उत्तर निकालिए। इससे इस कथन की व्याख्या कीजिए कि अति उच्च आवृत्ति पर किसी परिपथ में प्रेरक लगभग खुले परिपथ के तुल्य होता है। स्थिर अवस्था के पश्चात् किसी dc परिपथ में प्रेरक किस प्रकार का व्यवहार करता है?
उत्तर:
हल-दिया गया है-
Erms = 240 V
a. c. की आवृत्ति = f = 10 kHz
f = 10 × 103 Hz
f = 104 Hz
∴ ω = 2πf
= 2π × 104 rad s-1
और E0 = √2Erms
= √2 × 240V
L = 0.50 H, R = 100 Ω
∴ LR परिपथ की प्रतिबाधा.

स्पष्टतः उच्च आवृत्ति पर प्रेरणिक प्रतिघात XL = ωL अत्यधिक हो जाता है जिससे परिपथ में अत्यल्प मान की धारा प्रवाहित होती है तथा परिपथ लगभग खुले परिपथ के तुल्य होता है। dc परिपथ में ω = 0 अतः XL = 0 अतः प्रेरक एक शुद्ध चालक की तरह व्यवहार करता है।

![]()
प्रश्न 7.15.
40 Ω प्रतिरोध के श्रेणीक्रम में एक 100 µF के संधारित्र को 110 V, 60 Hz की आपूर्ति से जोड़ा गया है।
(a) परिपथ में अधिकतम धारा कितनी होगी?
(b) धारा शीर्ष व वोल्टेज शीर्ष के बीच समय-पश्चता कितनी होगी?
उत्तर:
हल-CR परिपथ के लिए यदि E = E0 cos ωt तब
I = I0 cos (ωt – Φ)
जहाँ पर I0 = \(\frac{E_0}{\sqrt{R^2+\frac{1}{\omega^2 C^2}}}\)
और tan Φ = \(\frac{1}{\omega C R}\)
(a) दिया गया है – R = 40 Ω
C = 100 μF = 100 × 10-6 F
C = 10-4 F
Erms = 110 V, f = 60 Hz
ω = 2πf
= 2π × 60 = 120 π rad s-1

प्रश्न 7.16.
यदि परिपथ को 110 V, 12 kHz आपूर्ति से जोड़ा जाए तो प्रश्न. 7.15 (a) और (b) का उत्तर निकालिए। इससे इस कथन की व्याख्या कीजिए कि अति उच्च आवृत्तियों पर एक संधारित्र चालक होता है। इसकी तुलना उस व्यवहार से कीजिए जो किसी dc परिपथ में एक संधारित्र प्रदर्शित करता है।
उत्तर:
हल-दिया गया है-
Erms = 110V, R = 40 Ω
C = 100 μF = 100 × 10-6 F = 10-4 F
f = 12 kHz = 12 × 103 Hz
∴ ω = 2πf
= 2π × 12 × 103 rad s-1
= 24π × 103 rad s-1
E0 = √2Erms
= √2 × 110V
(a) अधिकतम धारा I0
I0 = [/latex]\frac{E_0}{Z}[/latex] द्वारा दी जाती है।
यहाँ पर CR परिपथ के लिए Z का मान होगा-

(b) एक RC परिपथ में वोल्टता की कला, धारा की कला से Φ कोण से पीछे होती है
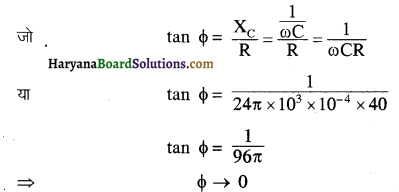
स्पष्टतः उच्च आवृत्ति पर संधारित्र एक चालक की तरह व्यवहार करता है जबकि दिष्ट धारा के लिये ω = 0 होने के कारण XC = \(\frac{1}{\omega C}\) = ∞ तथा दिष्ट धारा के लिये संधारित्र युक्त परिपथ एक खुला परिपथ होता है।
![]()
प्रश्न 7.17.
र्रोत की आवृत्ति को एक श्रेणीबद्ध LCR परिपथ के अनुनादी आवृत्ति के बराबर रखते हुए तीन अवयवो L,C तथा R को समान्तर क्रम में लगाते हैं। यह दर्शाइए कि समान्तर LCR परिपथ में इस आवृत्ति पर कुल धारा न्यूनतम है। इस आवृत्ति के लिए अभ्यास 7.11 में निर्दिष्ट र्रोत तथा अवयवों के लिए परिपथ की हर शाखा में धारा के rms मान को परिकलित कीजिए।
उत्तर:
हल-दिया गया है L = 5.0 H
C = 80 μF = 80 × 10-6 F
= 8 × 10-5 F
R = 40 Ω
समान्तर LCR परिपथ की प्रभावी प्रतिबाधा
\(\frac{1}{\mathrm{Z}}=\sqrt{\frac{1}{\mathrm{R}^2}+\left(\omega \mathrm{C}-\frac{1}{\omega \mathrm{L}}\right)^2}\) से प्रदर्शित करते हैं
जो कि ω = ω0 = \(\frac{1}{\sqrt{\mathrm{LC}}}\) पर न्यूनतम होगी
∴ω = ωr पर |Z| अधिकतम होगा। इसलिए कुल धारा का आयाम न्यूनतम होगा ।
समान्तर LCR परिपथ में I धारा IL, IC व IRके योग के बराबर होगी।

प्रश्न 7.18.
एक परिपथ को जिसमें 80 mH का एक प्रेरक तथा 60 μF का संधारित्र श्रेणीक्रम में है, 230 V, 50 Hz की आपूर्ति से जोड़ा गया है। परिपथ का प्रतिरोध नगण्य है।
(a) धारा का आयाम तथा rms मानों को निकालिए।
(b) हर अवयव के सिरों पर विभवपात के rms मानों को निकालिए।
(c) प्रेरक में स्थानान्तरित माध्य शक्ति कितनी है?
(d) संधारित्र में स्थानान्तरित माध्य शक्ति कितनी है?
(e) परिपथ द्वारा अवशोषित कुल माध्य शक्ति कितनी है?
(‘माध्य में यह समाविष्ट है’ कि इसे ‘पूरे चक्र’ के लिए लिया गया है।)
उत्तर:
हल-दिया गया है-
L = 80 mH = 80 × 10-3 H
= 8 × 10-2 H
C = 60 μF = 60 × 10-6 F
= 6 × 10-5 F
Erms = 230 V, f = 50 Hz

(b) L के सिरों पर Erms = Irms × ωL
= 8. 24 × 25. 14
= 207 V
C के सिरों पर Erms = Irms × \(\frac{1}{\omega C}\)
= 8. 24 × 53. 03
= 436.8 V
= 437 V
(c) L में धारा I चाहे कुछ भी हो, वास्तविक वोल्टता धारा से \(\frac{\pi}{2}\) अग्र है अतः C द्वारा उपभुक्त माध्य शक्ति शून्य है।
(d) C हेतु वोल्टता धारा के \(\frac{\pi}{2}\) पश्च है। पुनः C द्वारा उपभुक्त माध्य शक्ति शून्य है।
(e) चूँकि परिपथ का प्रतिरोध नगण्य है। कुल औसत उपभुक्त
शक्ति =L द्वारा उपभुक्त माध्य शक्ति +C द्वारा उपभुक्त माध्य शक्ति = 0 शुन्य
प्रश्न 7.19.
कल्पना कीजिए कि अभ्यास 7.18 में प्रतिरोध 15 Ω है। परिपथ के हर अवयव को स्थानान्तरित माध्य शक्ति तथा सम्पूर्ण अवशोषित शक्ति को परिकलित कीजिए।
उत्तर:
हल-दिया गया है-R = 15 Ω
L = 80 mH = 8 × 10-2 H
C = 60 μF = 6 × -5 F
Erms = 230 V
f = 50 Hz
∴ ω 2πf = 2π × 50 = 100 π
∴LCR परिपथ की प्रतिबाधा = Z

![]()
प्रश्न 7.20. एक श्रेणीबद्ध LCR परिपथ को जिसमें
L = 0.12 H, C = 480 nF, R = 23 Ω, 230 V परिवर्ती आवृत्ति वाले स्रोत से जोड़ा गया है।
(a) र्रोत की वह आवृत्ति कितनी है जिस पर धारा आयाम अधिकतम है। इस अधिकतम मान को निकालिए।
(b) स्रोत की वह आवृत्ति कितनी है जिसके लिए परिपथ द्वारा अवशोषित माध्य शक्ति अधिकतम है।
(c) स्रोत की किस आवृत्ति के लिए परिपथ को स्थानान्तरित शक्ति अनुनादी आवृत्ति की शक्ति की आधी है?
उत्तर:
(d) दिए गए परिपथ के लिए Q कारक कितना है?
हल-दिया गया है- L = 0.12 H
C = 480 nF = 480 × 10-9 F
R = 23 Ω
Erms = 230 V
(a) जब धारा आयाम अधिकतम है, स्रोत आवृत्ति, अनुनादी आवृत्ति के बराबर होती है = ?

(b) जब आवृत्ति अनुनादी आवृत्ति के बराबर है परिपथ द्वारा अवशोषित माध्य शक्ति अधिकतम है और दी जाती है।
\(\mathrm{P}_{\max }=\frac{1}{2} \mathrm{I}_0^2 \mathrm{R}\)
= \(\frac{1}{2}\) × (14.14)2 × 23
= 2300 वाट (लगभग)
(c) ω = ωr + ∆ω
अवशोषित ऊर्जा, [/latex]\frac{1}{2}[/latex] शिखर मान के बराबर है अर्थात् 663 Hz पर ।
हम यह सिद्ध कर सकते हैं।

प्रश्न 7.21.
एक श्रेणीबद्ध LCR परिपथ के लिए जिसमें L = 3.0 H, C = 27 μF तथा R = 7.4 Ω अनुनादी आवृत्ति तथा Q कारक निकालिए। परिपथ के अनुनाद की तीक्ष्णता को सुधारने की इच्छा से ‘अर्द्ध उच्चिष्ठ पर पूर्ण चौड़ाई’ को 2 गुणक द्वारा घटा दिया जाता है। इसके लिए उचित उपाय सुझाइए।
उत्तर:
हल-दिया गया है- L = 3.0 H
C = 27 μF = 27 × 10-6 F
R = 7.4 Ω
आवृत्ति fr = ?, Q = ?
आवृत्ति fr = \(\frac{1}{2 \pi \sqrt{\mathrm{LC}}}\)

प्रश्न 7.22.
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) क्या किसी ac परिपथ में प्रयुक्त तात्क्षणिक वोल्टता परिपथ में श्रेणीक्रम में जोड़े गए अवयवों के सिरों पर तात्क्षणिक वोल्टताओं के बीजगणितीय योग के बराबर होता है? क्या यही बात rms वोल्टताओं में भी लागू होती है?
(b) प्रेरण कुण्डली के प्राथमिक परिपथ में एक संधारित्र का उपयोग करते हैं।
(c) एक प्रयुक्त वोल्टता संकेत एक de वोल्टता तथा उच्च आवृत्ति के एक ac वोल्टता के अध्यारोपण से निर्मित है। परिपथ एक श्रेणीबद्ध प्रेरक तथा संधारित्र से निर्मित है। दर्शाइए कि dc संकेत C तथा ac संकेत L के सिरे पर प्रकट होगा ।
(d) एक लैंप से श्रेणीक्रम में जुड़ी चोक को एक de लाइन से जोड़ा गया है। लैंप तेजी से चमकता है। चोक में लोहे के क्रोड को प्रवेश कराने पर लैंप की दीप्ति में कोई अन्तर नहीं पड़ता है। यदि एक ac लाइन से लैंप का संयोजन किया जाए तो तदनुसार प्रेक्षणों की प्रामुक्ति कीजिए ।
(e) ac मेंस के साथ कार्य करने वाली फ्लोरोसेंट ट्यूब में प्रयुक्त चोक कुण्डली की आवश्यकता क्यों होती है? चोक कुण्डली के स्थान पर सामान्य प्रतिरोधक का उपयोग क्यों नहीं होता है?
उत्तर:
(a) हाँ, यह rs वोल्टता के लिए सत्य नहीं है। चूँकि विभिन्न अवयवों के सिरों पर वोल्टता का मान समान कला में नहीं हो सकता है।
(b) जब परिपथ खण्डित किया जाता है तो उच्च प्रेरित धारा संधारित्र को आवेशित करने के लिए प्रयुक्त की जाती है जो चिंगारी (स्पार्क) का परिवर्जन करती है।
(c) दिष्ट धारा के लिए L की प्रतिबाधा उपेक्षणीय है और C की प्रतिबाधा बहुत अधिक (अनन्त) है। अतः दिष्ट धारा C के सिरे पर होती है। उच्च आवृत्ति प्रत्यावर्ती धारा के लिए L की प्रतिबाधा उच्च हो और C की बहुत कम अतः प्रत्यावर्ती धारा संकेत L के सिरे पर होता है।
(d) स्थायी अवस्था दिष्ट धारा के लिए L का कोई प्रभाव नहीं है, चाहे इसे लौह क्रोड के प्रयोग से क्यों न बढ़ाया जाए। प्रत्यावर्ती धारा के लिए लैम्प चोक की अतिरिक्त प्रतिबाधा के कारण धूमिल दिखाई पड़ेगा। यहाँ लौह क्रोड के विवेशन से चोक की प्रतिबाधा में वृद्धि होगी जिसके कारण बल्ब और अधिक धूमिल हो जाएगा।
(e) शक्ति का क्षय किए बिना एक चोक कुण्डली ट्यूब के परितः वोल्टेज को कम करता है। प्रतिरोधक ऊष्मा के रूप में शक्ति का क्षय करता है।
![]()
प्रश्न 7.23.
एक शक्ति संप्रेषण लाइन अपचयी ट्रांसफार्मर में जिसकी प्राथमिक कुण्डली में 4000 फेरे हैं, 2300 वोल्ट पर शक्ति निवेशित करती है। 230 V की निर्गत शक्ति प्राप्त करने के लिए द्वितीयक में कितने फेरे होने चाहिए?
उत्तर:
हल- Vp = V निवेशित = 2300 V
Np =4000
Vs = 230 V
Ns = ?
हम जानते हैं- \(\frac{V_s}{V_p}=\frac{N_s}{N_p}\)
या Ns = \(\frac{V_S N_P}{V_P}\)
मान रखने पर- Ns = [/latex]\frac{230 \times 4000}{2300}[/latex] = 400
अतः द्वितीयक कुण्डली में फेरों की संख्या = 400
प्रश्न 7.24.
एक जल विद्युत शक्ति संयंत्र में जल दाब शीर्ष 300 m की ऊँचाई पर है तथा उपलब्ध जल प्रवाह 100 mg है। यदि टर्बाइन जनित्र की दक्षता 60% हो, तो संयंत्र से उपलब्ध विद्युत शक्ति का आकलन कीजिए, g= 9.8 m s-2
उत्तर:
हल दिया गया है-
दाब शीर्ष (h) = 300m
दक्षता η = 60%
प्रवाहित जल का आयतन प्रति सेकण्ड = 100 m3 s-1
अर्थात् v = 100 m3/s
8 = 9.8 m/s2
जल का घनत्व = 1000 kg/m3
प्रति सेकण्ड प्रवाहित जल का द्रव्यमान
m = आयतन x घनत्व
= 100 × 1000
= 105 kg/s
जल की स्थितिज ऊर्जा (p.E) = mgh
जहाँ पर m = 105 kg/s
P.E = 105 × 9.8 × 300
= 29.4 × 107 Js-1 या वाट
η = 60%
संयंत्र से उपलब्ध विद्युत शक्ति = 29.4 × 107 × \(\frac{60}{100}\)
= 17.64 × 107 वाट
= 176.4 MW
![]()
प्रश्न 7.25.
440 V पर शक्ति उत्पादन करने वाले किसी विद्युत संयंत्र से 15 km दूर स्थित एक छोटे से कस्बे में 220 V पर 800 kW शक्ति की आवश्यकता है। विद्युत शक्ति ले जाने वाली दोनों तार की लाइनों का प्रतिरोध 0.5 Ω प्रति किलोमीटर है। कस्बे को उप-स्टेशन में लगे 4000 – 220 V अपचयी ट्रांसफार्मर से लाइन द्वारा शक्ति पहँचती है।
(a) ऊष्मा के रूप में लाइन से होने वाली शक्ति के क्षय का आकलन कीजिए।
(b) संयंत्र से कितनी शक्ति की आपूर्ति की जानी चाहिए, यदि क्षरण द्वारा शक्ति का क्षय नगण्य है।
(c) संयंत्र के उच्चायी ट्रांसफार्मर की विशेषता बताइए। हल-दिया गया है- दो तारों की लाइन की लम्बाई
उत्तर:
हल-दिया गया है- दो तारों की लाइन की लम्बाई = l = 15 × 2
l = 30 km.
तार की लाइन की इकाई लम्बाई का प्रतिरोध = 0.5 Ω/km.
दो तारों वाली लाइन का प्रतिरोध = R
R = 30 × 0.5
= 15 Ω
p = 800 kW
= 8 × 105 W
चूँकि 4000-220 V अपचायी परिणामित्र से शक्ति प्रदत्त है।
Erms = 4000 V = लाइन की प्राप्ति सिरे पर वोल्टता
माना लाइन धारा का मान = Irms = ?
p = Erms × Irms
⇒ Irms = \(\frac{\mathrm{P}}{\mathrm{E}_{\mathrm{rms}}}=\frac{8 \times 10^5}{4000}\)
⇒ Irms = 200 A
(a) लाइन में शक्ति हानि = \(\mathrm{I}_{\mathrm{rms}}^2 \mathrm{R}\)
= (200)2 × 15
= 40000 × 15
= 60 × 104 = 6 × 105
= 600 kW
(b) प्लान्ट द्वारा प्रदत्त शक्ति जबकि क्षरण के कारण कोई हानि नहीं है
= p + शक्ति हानि
= [ 800 + 600] × 103
= 1400 kW
(c) लाइन में वोल्टता-पात = Irms × R
= 20 × 15 = 300 V
∴ संयंत्र द्वारा विद्युत प्रदाय = प्राप्ति सिरे पर वोल्टता + लाइन में विभवपात
= 40000 + 300
= 7000 V
प्लान्ट 440 V पर शक्ति जनित करता है और इसे उपचायी भी करनी है जिससे लाइन में 3000 V पात के बाद भी शहर के विद्युत उपकेन्द्र में शक्ति 4000 V पर प्राप्त की जा सके।
∴ प्लान्ट पर उच्चायी परिणामित्र 440 V – 7000 V तक का उपलब्ध होना चाहिए।
प्रश्न 7.26.
ऊपर किए गए अभ्यास को पुन: कीजिए। इसमें पहले के ट्रांसफार्मर के स्थान पर 40,000-220 V का अपचयी ट्रांसफार्मर है। [पूर्व की भाँति क्षरण के कारण हानियों को नगण्य मानिए। यद्यपि अब यह सन्निकटन उचित नहीं है क्योंकि इसमें उच्च वोल्टता का संप्रेषण होता है]। अतः समझाइए कि क्यों उच्च वोल्टता संप्रेषण अधिक वरीय है?
हल-दिया गया है
Erms = 40000 V = 4 × 104 V
लाइन धारा = Irms = ?
शक्ति p = 800 kW = 8 × 105 W
∴Irms = \( \frac{P}{E_{\mathrm{rms}}}=\frac{8 \times 10^5}{4 \times 10^4}=20 \mathrm{~A}\)
(a) ऊष्मा के रूप में लाइन से होने वाली शक्ति का क्षय
= \(I_{\mathrm{rms}}^2 \times R\)
= (20)2 × 15
= 400 × 15 = 6000 w
= 6 kW
(b) संयंत्र द्वारा विद्युत प्रदाय = आवश्यक शक्ति + लाइन में शक्ति हानि
= 800 + 6 = 806 kW
(c) लाइन में विभवपात = Irms × R
= 20 × 15 = 300 V
प्रसारण के लिए वोल्टता = प्राप्ति सिरे पर वोल्टता + लाइन में विभवपात
= 40000 + 300
= 40300 V
संयंत्र के लिए उच्चायी ट्रांसफार्मर चाहिए 440 – 40300 V
स्पष्टीकरण-उच्च विभव पर \% शक्ति क्षय

स्पष्टतः उच्च वोल्टता पर संचरण से शक्ति क्षय कम होती है अतः संप्रेषण में उच्च वोल्टता संप्रेषण को वरीयता दी जाती है।