HBSE 10th Class Science Important Questions Chapter 12 Electricity

Haryana State Board HBSE 10th Class Science Important Questions Chapter 12 Electricity Important Questions and Answers.

Haryana Board 10th Class Science Important Questions Chapter 12 Electricity

Question 1.
What do you mean by electric charge?
Answer:
Electric charge:

• ‘Charge’ or ‘electric charge’ is the fundamental quantity of electricity.
• Electric charge or simply charge is of two types, (1) Positive (+) charge and (2) negative (-) charge.
• If electric charge flows through a conductor such as metal wire, we say that there is electric current in the conductor.
• Equal amount of positive (+ve) charge + Equal amount of negative (-ve) charge = zero (O)
• The SI. unit of electric charge is columb ‘C’.
• An electron possesses a ‘negative charge of 1.6 x 10^-19 C’ whereas a proton possesses a ‘positive charge of 1.6 x 10^-19 C’.

Question 2.
State the properties of electric charge.
Answer:
(A) Like charges repel each other i.e. when a proton-proton or electron-electron interact, they repel.
(B) Unlike charges attract each other ie. when a proton and an electron interact, they attract each other.

Question 3.
What is a free electron?
Answer:
1. Metals have a property to lose electrons and form positive ions.

2. The outer most electrons move randomly around the nucleus.

3. These electrons work as glue and bind the protons at their place and thus make them immovable.

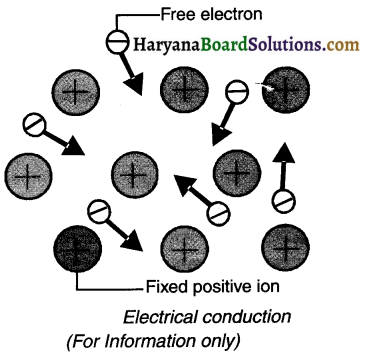
4. Under normal circumstances, in metallic materials the force of attraction between these outermost electrons (or say valence electrons) and the nucleus (which is positively charged) is quite less.

5. These electrons separate from their parent atom and move randomly.

6. These electrons are known as free (or conducting) electrons and are responsible for conducting electricity or say conduction.

7. Electric current can flow very easily through material which contain a large number of free electrons. Hence such a material is called a conductor. For example, metals such as copper, silver and aluminium are conductors.

Question 4.
Resolve the mystery behind the conventional current and actual flow of electric current. OR ‘In a circuit diagram, we put arrows on connecting wires pointing from the positive terminal of the cell to the negative terminal of the cell’. Explain. OR Explain conventional current and its flow.
Answer:
1. In the earlier times, when scientists did not have knowledge about electrons, it was thought that electric current was a flow of positive charge. Hence, the direction of flow of positive charges was considered as the direction of electric current. This flow came to be known as ‘conventional current’.

2. Later, negatively charged electrons were discovered and it was fund that electrons were responsible for the flow of electric current.

3. Thus, it was proved that the actual flow of electric charge was not from ‘positive to negative’ but from ‘negative to positive’.

4. However, in practice we still take direction of electric current as ‘positive to negative’ i.e. the path of conventional current. We do this by putting the arrows from positive terminal of batteries to negative terminal.

5. Thus, flow of conventional current (positive to negative) is opposite to the actual direction of flow of electrons (negative to positive).

Question 5.
Define electric current and state and explain its unit.
Answer:
Electric current:
1. The rate of flow of electric charge is known as electric current. In other words, the net quantity of electric charge that flows through any cross-section of a conductor is known as the electric current.
Thus? electric current \(=\frac{\text { Quantity of electric charge }}{\text { Time }}\)

2. Thus, if Q is the amount of electric charge passing through any cross-section of a conductor in time t then, electric current (I) = \(\frac{Q}{t}\)

3. If a quantity of one Coulomb (1Q) electric charge passes through the conductor in 1 second, then we can say that an electric current of one ampere (1A) is flowing through the conductor.

4. SI unit of electric current is Coulomb/second (C/s).

5. Electric current is also measured in Ampere (A), after the French scientist Andre-Marie Ampere.

6. Milliampere (mA) and microampere (.iA) are smaller units to measure electric current.

7. 1 mA = 10^-3 A and 1 μA = 10^-6 A.

8. An instrument called Ammeter is used to measure the electric current.

Question 6.
What is ampere? Explain.
Answer:
1. Ampere (A) is the main unit in which electric current is measured. The unit is Ampere (A) after the French scientist Andre Ampere.
2. Milliampere (mA) and microampere (pA) are smaller units to measure electric current.
3. 1 mA =10^-3 A and 1 μA = 10^-6 A.
4. An instrument called Ammeter is used to measure the electric current.
5. Ammeter is ‘connected in series’ in the electric circuit.

Question 7.
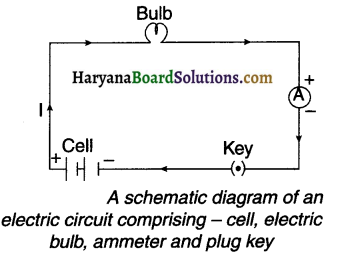
Draw a schematic diagram of an electric circuit and explain it.
Answer:
1. The figure shown here is a basic electric circuit. It comprises of a cell, an electric bulb, an ammeter (connected in series) and a key or say switch to control the circuit.

2. When key (switch) is turned on, the electric current starts flowing from positive terminal of the cell to the negative terminal, through the bulb and the ammeter.

3. The bulb will glow and ammeter will show a reading which ascertains flow of electric current in the circuit.

Question 8.
Define electric circuit and switch.
(a) Electric circuit:
A continuous and closed path along which electric current flows is called an electric circuit.

(b) Switch:
A switch is a component that provides a connecting link between the cell i.e. battery and other electrical components of electric circuit.

Question 9.
State the relationship between 1 ampere and 1 coulomb.
Answer:
If 1 coulomb charge passes through the conductor in 1 second, then we say that electric current of 1 ampere is flowing through the conductor.
1 ampere = \(\frac{1 \text { Coulomb }}{1 \text { Second }}\)
∴ \(1 A=\frac{1 C}{1 s}=1 \mathrm{Cs}^{-1}\)

Question 10.
State and explain the relation between quantity of charge and number of electrons flowing through a conductor.
Answer:
1. If the number of electrons passing through the cross-section of conductor in time ‘t’ equals to ‘n’, then the quantity of charge passing through the cross-section will be Q = ne.

2. In this sense, equation \(I=\frac{Q}{t}\) can be represented as \(I=\frac{n e}{t}\),
where e = 1.6 x 10^-9 C charge of electron.

Question 11.
How many electrons will be required to produce 1 Ampere electric current in a conductor?
Answer:
1. If 1 coulomb electric charge i.e. Q passes through a conductor in 1 second, then 1 Ampere electric current will flow through the conductor.

2. Now, current I = 1A, charge Q = 1C and time t = 1s

3. We know that Q = ne (where e = 1.6 x 10^-19 C)
Also we know that I\(=\frac{Q}{t}=\frac{n e}{t}\)
∴ No.of electrons \(\mathrm{n}=\frac{\mathrm{l} . t}{\mathrm{e}}=\frac{1 \times 1}{1.6 \times 10^{-19}}\)
= 6.25 x 10¹⁸

4. Thus, 6.25 x 10¹⁸ electrons will be required to produce 1 Ampere electric current in a conductor.

Question 12.
A current of 0.5 A is drawn by a filament of an electric bulb for 10 minutes. Find the amount of electric charge that flows through the circuit.
Answer:
We are given, I = 0.5 A, t = 10 min = 600 s.
Now, Q = It = 0.5 A x 600 s= 300 C

Question 13.
While connecting a torch with battery, an electric current of 64 mA flows through the bulb. If this torch glows for 10 mm, how many electrons will pass through the bulb? (charge of electron =e = 1.6 x 10^-19 C)
Answer:
I = 64 mA = 64 x 10^-3A,t = 10min = 10 x 60
=600s, e=1.6 x 10^-19 C

= 24000 x 10¹⁶
n = 24 x 10¹⁹ electrons

Question 14.
1800 C electric charge is passing through an electric bulb in one hour. How much current will pass through the electric bulb?
Answer:
Q = 1800 C, time t = 1 hr = 3600s
Electric current \(I=\frac{Q}{t}=\frac{1800}{3600}=0.5\) current will pass through the electric bulb.

Question 15.
Give a general idea of electric potential and electrical potential difference.
Answer:
1. As shown in the figure, pour larger quantity of water in vessel A and lesser quantity of water in vessel B. Connect these two vessels with a tube.

2. Vessel A contains more water than vessel B and so water in vessel A will have higher pressure.

3. Hence, water will flow from vessel A to vessel B. In other words, water flows through the tube due to ‘water pressure difference’ or say ‘water potential difference’.

4. Similarly, if an ‘electric potential difference’ is created between two points, then the electric current can also be made to flow from one point to another.

5. The difference in electric potential that exists between the two points is known as electric potential difference.

Electric potential:

• When you bring some electric charge near another charge, the former charge may experience a force of attraction or repulsion. So, work has to be done to move it against the force of repulsion or towards the force of attraction.
• In other words, in order to maintain equilibrium between these two charges, some work has to be done.
• This work is stored in the form of potential energy.
• The work done on the charge is called electric potential.

Question 16.
What is electric potential difference? Explain the unit used for measuring potential difference.
Answer:
(a) Electric potential difference:
The amount of work done to take a unit positive charge from a given point say A to point B in a circuit carrying some current is known as the electrical potential difference between the two points.
→ Thus, electric potential difference \((V)=\frac{\text { Work done }(W)}{\text { Electric charge }(Q)}\)
\( \quad V=\frac{W}{Q}\)

(b) Voltage:
(1) In practice, electric potential difference is known as voltage. Its SI unit is joule/coulomb or volt (V).
(2) If the work done to bring 1-coulomb electric charge from one point to another is 1 joule, then the potential difference between these two points is called 1 volt. (V)
Thus, 1 volt \(=\frac{1 \text { joule }}{1 \text { Coulomb }}\) \(1 \mathrm{~V}=1 \mathrm{JC}^{-1}\)
(3) Electric potential difference (V) is measured with a device called voltmeter.
(4) The voltmeter is connected in parallel across the two points of which the potential difference is measured.

Question 17.
Define electric potential and state its unit.
Answer:
Electric potential difference:
The amount of work done to take a unit positive charge from a given point say A to point B in a circuit carrying some current is known as the electrical potential difference between the two points.
→ Thus, electric potential difference \((V)=\frac{\text { Work done }(W)}{\text { Electric charge }(Q)} \)
\(\quad V=\frac{W}{Q}\)

Question 18.
Define 1 volt and state its unit. OR what is voltmeter? How is It connected in an electric circuit?
Answer:
Voltage:
(1) In practice, electric potential difference is known as voltage. Its SI unit is joule/coulomb or volt (V).

(2) If the work done to bring 1-coulomb electric charge from one point to another is 1 joule, then the potential difference between these two points is called 1 volt. (V)
Thus, 1 volt \(=\frac{1 \text { joule }}{1 \text { Coulomb }}\) \(1 \mathrm{~V}=1 \mathrm{JC}^{-1}\)

(3) Electric potential difference (V) is measured with a device called voltmeter.

(4) The voltmeter is connected in parallel across the two points of which the potential difference is measured.

Question 19.
Name the device used to measure electric potential difference and state how it is connected in an electric circuit.
Answer:
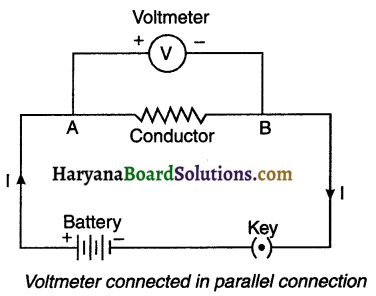
Voltmeter:
1. The device used to measure potential difference between any two points of a circuit is called voltmeter (Volt + meter).
2. Voltmeter is connected in a parallel connection.

Question 20.
List two differences between voltmeter and ammeter.
Answer:

Voltmeter	Ammeter
1. It measures potential difference between two points in a circuit.	1. It measures potential difference between two points in a circuit.
2. It is connected in parallel with the component across which potential difference is to be measured.	2. It is connected in parallel with the component across which potential difference is to be measured.
1 Volt = \(\frac{1 \text { joule }}{1 \text { coulomb }}\)	1 ammeter =\(\frac{1 \text { coulomb }}{1 \text { second }}\)

Question 21.
How much work Is done in moving a charge of 2 C across two points having a potential difference 12 V?
Answer:
The amount of charge Q, that flows between two points at potential difference V (= 12 V) is 2 C.
Thus, the amount of work W, done in moving the charge is W = VQ = 12 V x 2C = 24J.

Question 22.
How much work is to be done to take 2 C electric charge from the potential of 6 V to the potential of 12 V?
Q=2C
Electric potential difference V = 12V – 6V = 6V
Now \(V=\frac{W}{Q}\)
∴ Work W = VQ = 6 x 2 = 12J

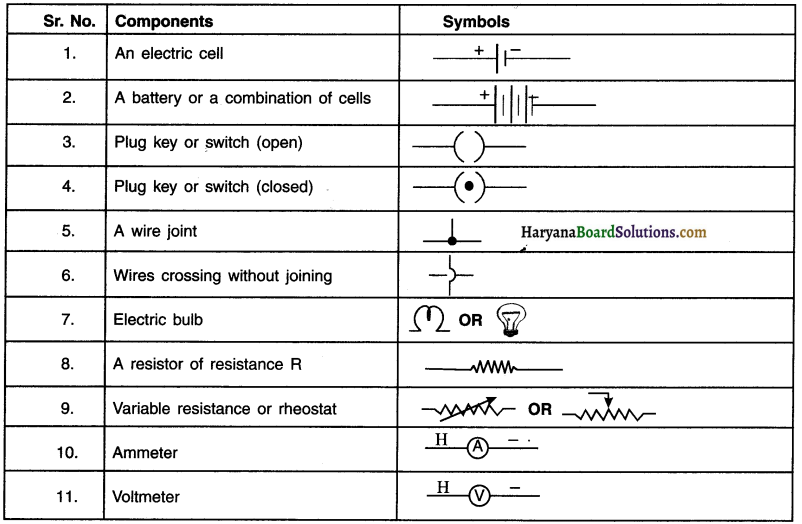
Symbols of some commonly used components in circuit diagrams

Question 23.
Perform an activity to verify Ohm’s law
Answer:
Aim: Verification of Ohm’s law
Apparatus and material : 0.5 meter long nichrome wire (or an electric bulb), batteries of 1.5 V, voltmeter, ammeter and key.

Procedure:

1. Prepare an electric circuit by connecting XV nichrome wire (or an electric bulb) as resistance first with one 1.5 V battery, ammeter and a key.
2. Then connect voltmeter between two ends of wire as shown.
3. When you switch on the key, the electric current will flow through the circuit.
4. Measure the current (I) in ammeter and potential difference (V) in the voltmeter.
5. Similarly, connect two, three and finally four batteries in the circuit and each time measure the values of current I and voltage V.
6. Record all the values of I and V in the table.

Observation table:

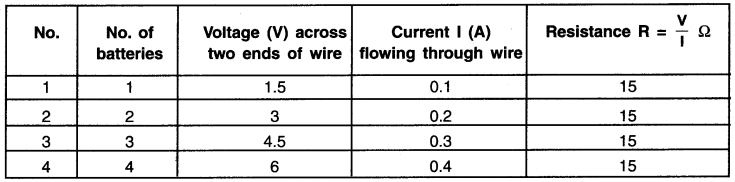
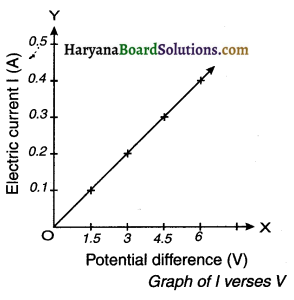
Plot values of V and I on the graph.

Conclusion:

1. On plotting these values we observe that the graph is a straight line passing through the origin.
2. As you increase the number of batteries, the electric current in the conductor increases in a constant proportion with the increase in voltage V.
3. The ratio of V and I i.e. VII always remains constant.

Question 24.
State Ohm’s law and explain its unit.
Answer:
Ohm’s law:
1. In a definite physical situation, the electric current (I) flowing through the conductor is directly proportional to the potential difference (V) applied across it, provided its temperature and other physical conditions remain same.

2. Thus, I α V or say V α I.
∴ V = I R (where, R is the proportionality by constant and it represents resistance R of the circuit)
V/I = Constant Also, Resistance \((\mathrm{R})=\frac{\text { Voltage }(\mathrm{V})}{\text { Electric current }(\mathrm{l})}\)

3. The SI unit of resistance is volt/ampere which is called ohm and it is denoted by Ω (Omega).
∴ 1 ohm \((\Omega)=\frac{1 \text { volt }(V)}{1 \text { ampere }(i)}\)

4. When 1 volt potential difference (V) is applied across the conductor and 1 ampere (I) current flows through it, then resistance of the conductor is said to be 12.

5. The symbol represents resistance R in the circuit.

Question 25.
Discuss the factors on which strength of electric current ¡n a given conductor depends. OR How can you say that the current flowing in a circuit is strong or weak? Discuss.
Answer:
Ohms law says, current \((\mathrm{I})=\frac{\mathrm{V} \text { (Potential difference) }}{\mathrm{R} \text { (Resistance) }}\)

From this relation we draw two conclusions. They are –
(i) I α V (if R = constant) (ii) I α\(\frac{1}{R}\)(if V = constant)

From 1st:
1. Since, current (I) is directly proportional to potential difference V, if value of V is doubled, the current (I) flowing through it will also get doubled.
2. If V is halved, the current will also get halved,

From 2nd:
1. Current (I) is inversely proportional to resistance (R). So, if the value of resistance is doubled, the current (I) flowing will get halved.
2. If resistance is halved, the current (I) will get doubled.

Conclusion:
The strength of electric current in a given conductor depends on —
(i) Potential difference (V) across the ends of the conductor (ii) Resistance (R) of the conductor

Question 26.
Define resistance and variable resistance and bring out the difference between resistance and resistor
Answer:
(a) Resistance:
1. Resistance refers to the property of the conductor by virtue of which it opposes the flow of current through it.

2. Resistance is equal to the ratio of potential difference applied across the conductor to the current flowing through it.
Thus, Resistance \((\mathrm{R})=\frac{\text { Potentialdifference }(\mathrm{V})}{\text { Current }(\mathrm{l})} \quad\)
∴ \(\mathrm{R}=\frac{\mathrm{V}}{\mathrm{l}}\)

(b) Vanable resistance:
1. A component used for regulating (i.e. increasing or decreasing) the current without changing the voltage source is called a variable resistor and the concept is called variable resistance.

2. In other words, variable resistance allows us to adjust the resistance between two points in a circuit. Rheostat is one such device that helps to change resistance in the circuit. Thus, resistor creates resistance.

Question 27.
Explain the cause of resistance in conductors and insulators.
Answer:
1. Flow of free electrons In a fixed direction results in flow of electric current in a conductor.
2. These freely moving electrons collide with atoms or molecules of conductor. This retards their motion.
3. Motion of electrons means that the electric current gets opposed. This is called resistance (R) of the conductor.
4. Metals such as aluminum, steel, copper, etc. have a large number of free electrons and so they offer low resistance to the flow of electric current. Metals are good conductors.
5. Insulators such as wood, plastic, rubber, etc. do not have free electrons. Hence, no current flows through them. So, their resistance is very high. Insulators are poor conductors.

Question 28.
Define resistance (resistivity) of a substance and explain its unit.
Answer:
1. The resistance (R) of a conductor is directly proportional to the length of the conductor and inversely proportional to the area of its cross-section.

2.  Let the length of the conductor be I and its cross-sectional area be A, then,
Resistance R α length l arid also R α \(\frac{1}{A}\)
∴ \(R \alpha \frac{I}{A}=\rho \frac{I}{A}\) = (where ρ (rho) is constant and called the resistivity of conducting material.)

3. We can also say, ρ = \(R \frac{A}{l}\)

4. The S.l unit of resistivity \(\rho=\frac{\text { Unit of resistance } x \text { Unit of area }}{\text { Unit of length }}=\frac{\Omega \mathrm{xm}^2}{\mathrm{~m}}=\Omega \mathrm{m} \text { (Ohm meter) }\)

Question 29.
List the factors on which the resistance of a conductor depends. Write the formula showing relation of resistance with these factors.
Answer:
At constant temperature, the resistance of a conductor depends on the following factors:
(i) Length: Resistance R of a conductor is directly proportional to its length L i.e. R α L
(ii) Area of cross-section: Resistance R of a conductor is inversely proportional to the area of cross-section A i.e, \(R \propto \frac{1}{A}\)
(iii) Nature of material: Resistance depends on the nature of material. For example, resistance of copper wire is quite less as compared to nichrome wire.

Combining all these factors we get —
R α \(\frac{L}{A}\)  or say R = ρ\(\frac{L}{A}\) (Where p is the proportionality constant and is called ‘resistivity’ or ‘specific resistance’ which depends on the nature of the material.)

Question 30.
Classify solids on the basis of their resistivity values.
Answer:
On the basis of resistivity values, we can classify solids as:
(i) Conductors (metals and alloys):

• Metals and their alloys have very low resistivity in the range of 10^-8 to 10^-6 Ω m.
• These are known as good conductors of electricity.
• Copper, aluminium, iron, etc. are metals. Nichrome, constantan, manganin, etc. are metallic alloys.

(ii) Insulators:

• Insulators are substances that have very large resistivity. They have resistivity of more than 1 m. Insulators such as glass, hard rubber, etc. have very high resistivity range of 10¹² to 10¹⁷ Ωm.

Electrical resistivity of some substances at 200 C. (For information only)

You need not memorize these values. You can use these values for solving numerical problems.

Question 31.
Differentiate between Conductors and Insulators.
Answer:

Conductors	Insulators
Conductors contain large number of free electrons.	Insulators do not contain free electrons
Conductors can conduct electricity.	Insulator cannot conduct electricity.
Metallic elements like silver, aluminium, copper etc. are conductors.	Rubber, plastic, etc. are insulators.

Question 32.
(a) How much current will an electric bulb draw from a 220 V source, If the resistance of the bulb filament is 1200 Ω? (b) How much current will an electric heater coil draw from a 220 V source, If the resistance of the heater coil is 100 Ω? (Text book example 12.3)
Answer:
(a) We are given V = 220 V; R = 1200Ω We have current I = 220 V/1200 Ω = 0.18 A.
(b) We are given, V = 220 V, R = 100Ω. We have current I = 220 V/100 Ω = 2.2 A.

Question 33.
The potential difference between the terminals of an electric heater is 60 V when it draws a current of 4 A from the source. What current will the heater draw If the potential difference is increased to 120 V? (Text book example 12.4)
Answer:
We are given, potential difference V = 60 V, current I = 4 A.
According to Ohm’s law, \(R=\frac{V}{l}=\frac{60 \mathrm{~V}}{4 \mathrm{~A}}=15 \Omega\)
When the potential difference is increased to 120 V the current is given by —
current = \(\frac{V}{R}=\frac{120 V}{15 \Omega}=8 A\)
The current through the heater becomes 8 A.

Question 34.
Resistance of a metal wire of length 1 m is 26Ω at 20°C. lithe diameter of the wire is 0.3 mm, what will be the resistivity of the metal at that temperature? Using Table 12.2, predict the material of the wire. (Text book example 12.5)
Answer:
We are given the resistance R of the wire = 26Ω, diameter = 0.3 mm = 3 x 10 m, and the length I of the wire = 1m.
Therefore, the resistivity of the given metallic wire is ρ= (RA/I) = (Rπd²/4l)
Substitution of values in this gives ρ = 1.84 x 10^-6 Ωm
The resistivity of the metal at 20°C is 1.84 x 10^-6 Ωm.

We are given, potential difference V = 60 V, current I = 4 A.
According to Ohm’s law, \(R=\frac{V}{l}=\frac{60 \mathrm{~V}}{4 \mathrm{~A}}=15 \Omega\)
When the potential difference is increased to 120 V the current is given by —
current = \(\frac{V}{R}=\frac{120 V}{15 \Omega}=8 A\)
The current through the heater becomes 8 A.

Question 35.
A wire of given material having length I and area of cross-section A has a resistance of 4 ? What would be the resistance of another wire of the same material having length 1/2 and area of cross-section 2A? (Text book example 12.6)
Answer:
For first wire

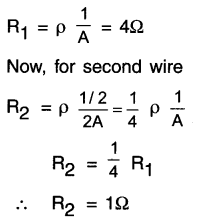
The resistance of the new wire is 1Ω.

Question 36.
If an electric bulb connected to 220 V line draws an electric current of 0.5 A, then what will be the resistance of the filament of the bulb?
Answer:
I = 0.5A,V=220V
According to Ohm’s law, \(R=\frac{V}{l}=\frac{220}{0.5}=440 \Omega\)

Question 37.
The resistance of a resistive wire having length l and area of cross-section A is 4Ω. If the length of same type of wire is 1/2 and the area of cross-section 2A, what will be the resistance of wire?
Answer:
For the first wire \(R=\rho \frac{l}{A}\)-, for the second wire,\(\mathrm{R}^{\prime}=\rho^{\prime} \frac{I^{\prime}}{\mathrm{A}^{\prime}}\)

Question 38.
There are more than one ways of combining resistors in a circuit. Explain them very briefly.
OR Why does the need of combining resistors in more than one way arises in a circuit?
Answer:
1. Apart from potential difference, current in circuit also depends on resistance R.

2. All electrical circuits do not require the same amount of resistance.

3. In order to obtain the desired resistance, resistors need to be connected in two different ways.
They are: Connecting resistors in (A) series and in (B) parallel.

4. If we want to increase total resistance, then we need to connect the resistors in series and if we want to decrease the resistance, we need to connect individual resistors in parallel.

Question 39.
With the help of suitable diagrams state the two methods of connecting resistors in a circuit. There are two methods of joining the resistors. They are:

(1) Joining resistors In a series connection:

• When two or more resistors are connected end-to-end consecutively, such a connection is called a series connection.
• As shown in the figure, three resistors R₁, R₂ and R₃ are connected end-to-end.

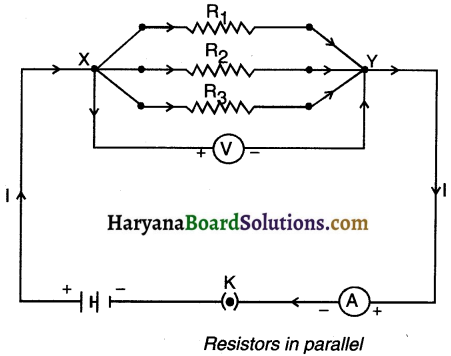
(2) Joining resistors in a parallel connection:

• When two or more resistors are connected between the same two points of a circuit, they are said to be connected in a parallel connection (because they are connected in parallel and not end-to-end).
• The diagram here shows resistors R₁, R₂ and R₃ connected in parallel between the two points A and B.

Question 40.
Explain the series connection of resistors and derive the formula of equivalent resistance.
Answer:
Series connection of resistors:
1. When two or more resistors are connected end-to-end consecutively such a connection is called a series A connection.

2. As shown in figure, consider three resistances R₁, R₂ and R₃ connected in senes. Suppose a current I flows through the circuit when a cell of voltage V is connected across the combination.

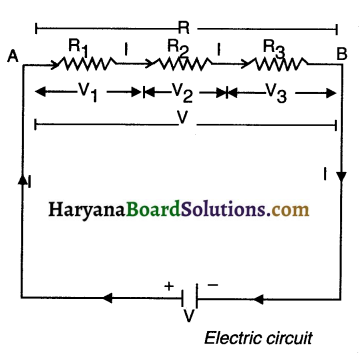
By Ohm’s law, the potential differences across the three resistances will be,
V₁ = IR₁, V₂ = IR₂, V₃ = IR₃,

If R be the equivalent resistance of the senes combination, then on applying a potential difference V across it, the same current I must flow through it. Therefore,
V = IR
But V=V₁ + V₂ +V₂
∴ IR_S = IR₁ + IR₂ + IR₂ OR R_s = R₁ + R₂ + R₃

Question 41.
State the characteristics of series connection of resistors.
Answer:
1. In series connection of resistors, the current (I) flowing through each resistance is same.
2. The total voltage drop across all the resistances connected in series equals to the sum of voltage drop across each resistance Le. V = V₁ + V₂ + …………………………. + V_n.
3. The equivalent resistance of resistors connected in series is equal to the algebraic sum of all resistors.
4. The magnitude of equivalent resistance i.e. R is always larger than the largest resistance of the circuit. In other words, equivalent resistance R is larger than any other resistance of the circuit.

Question 42.
An electric lamp, whose resistance is 20Ω and a conductor of 4Ω resistance are connected to a 6 V battery (as shown In figure). Calculate (a) the total resistance of the circuit, (b) the current through the circuit, and (c) the potential difference across the electric lamp and conductor.
Answer:

The resistance of electric lamp, R₁ = 20Ω
The resistance of the conductor connected in series, R₂ = 4Ω
Then the total resistance in the circuit
R =R₁ + R₂
R_s =20Ω + 4Ω=24Ω
The total potential difference across the two terminals of the battery
V = 6V.
Now by Ohm’s law, the current through the circuit is given by
I =V/Rs=6V/24.Ω = 0.25A.
Applying Ohm’s law to the electric lamp and conductor separately, we get potential difference across the electric lamp,
V₁ =20Ω 2 x 0.25A = 5V;
Potential difference across the conductor, V₂ = 4Ω x 0.25 A = 1 V.
Suppose we replace the series combination of electric lamp and conductor by a single and equivalent resistor. Its resistance must be such that a potential difference of 6 V across the battery terminals will cause a current of 0.25 A in the circuit. The resistance R of this equivalent resistor would be
R =V/l = 6V/0.25A = 24Ω
This is the total resistance of the series circuit. It is equal to the sum of the two resistances.

Question 43.
In order to get the current 0.5 A in the circuit by connecting a bulb of resistance 20Ω with 12 V battery, how much should be the value of resistance connected in series? What will be the voltage drop across the bulb?
Answer:
If the resistance connected in series with bulb is R₁ and resistance of bulb is R₂ then the circuit will be as shown in the figure here.
V=12 V, l=0.5A, R₂=20Ω, R₁=?

Using Ohm’s law,
Here, bulb and R1 are in series,\(R=\frac{V}{J}=\frac{12}{0.5}=24 \Omega\)
therefore equivalent resistance
R=R₁+R₂ ……………………… (1)
Substituting the value of R and R₂ in equation (1)
24=20+R₂
∴ R₂ = 24 – 20 = 4Ω
The voltage drop across the bulb, V₂ = IR₂ = (0.5) (4) = 2 V

Question 44.
When an electric heater is given a voltage 120 V, an electric current of 2 A passes through It. If the heater is given a voltage of 240 V, how much electric current will flow through it? What will be the resistance of the coil of the heater?
V₁ = 120V, I₁ = 2A, V₂ = 240V, I₁ =?
Answer:
Resistance of heater coil \(R=\frac{V_1}{L_1}=\frac{120}{2}=60 \Omega\)
Now, according to Ohms’ law,

Question 45.
Define parallel connection of resistances and derive the resistance equation for equivalent resistance.
Answer:
1. When two or more resistances are connected between the same two points of a circuit, the resistances are said to be connected in parallel.

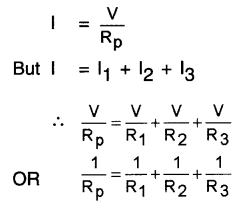
2. As shown in figure, consider three resistances R₁, R₂ and R₃ connected in parallel. Suppose a current I flows through the circuit when a cell of voltage V is connected across the combination.

3. The current I at point A is divided into three parts l₁, l₂ and l₃ through the resistances R₁, R₂ and R₃ respectively.
These three parts recombine at point B to give the same current I. Total current flowing in the circuit,
l=l₁+ l₂ + l₃

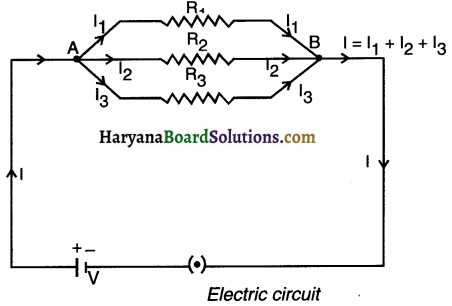
As all the three resistances have been connected between the same two points A and B, so voltage V across each of them is same. By Ohm’s law,
\(I 1=\frac{V}{R_1}, \quad 12=\frac{V}{R_2}, \quad I 3=\frac{V}{R_3}\)

If Rp be the equivalent resistance of the parallel combination, then,

Question 46.
State the characteristics of parallel connection of resistors.
Answer:
1. The sum of the current flowing through each resistor equals to total current flowing ¡n the circuit
i.e. l=l₁+ l₂ + …………………. +l_n
2. The voltage drop across each resistor remains the same.
3. The magnitude of equivalent resistance i.e. R is always smaller than the smallest resistance.
4. The reciprocal of equivalent resistance R is equal to the sum of reciprocal of individual resistors
i.e \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\ldots \ldots \ldots \ldots+\frac{1}{R_n}\)

Question 47.
In the circuit diagram given in figure  suppose the resistors R₁, R₂ and R₃ have the values 5Ω, 10Ω, 30Ω, respectively, which have been connected to a battery of 12 V. Calculate (a) the current through each resistor, (b) the total current In the circuit, and (c) the total circuit resistance. (Textbook Example – 12.8)
Answer:
R₁=5Ω, R₂=10Ω and R₃=30Ω
Potential difference across the battery, V = 12 V.
This is also the potential difference across each of the individual resistor; therefore, to calculate
the current in the resistors, we use Ohm’s law.
The current l., through R₁ = V/R₁
l₁ =12 V/5Ω = 2.4 A.
The current 12, through R₁ = V/R₁
I₂ =12 V/10Ω = 1.2 A.
The current I₃, through R₃ = V/R₃
I₃ =12 V/30Ω = 0.4A.
The total current in the circuit,
I =I₁ +I₂+I₃=(2.4+1.2+0.4)A = 4A
The total resistance is given by
\(\frac{1}{R_p}=\frac{1}{5}+\frac{1}{10}+\frac{1}{30}=\frac{1}{3}\)
Thus, R_P = 3Ω.

Question 48.
lf in given figure R₁=10Ω, R₂=40Ω, R₃=30Ω, R₄=20Ω, R₅=60Ω, and a 12V battery is connected to the arrangement. Calculate (a) the total resistance In the circuit, and (b) the total current flowing in the circuit. (Textbook Example 12.9)
Answer:
Suppose we replace the parallel resistors R₁ and R₂ by an equivalent resistor of resistance, R’. Similarly we replace the
parallel resistors R₃, R₄ and R₅ by an equivalent single resistor of resistance R₁. Then, we have
1/R’ = 1/10 + 1/40 = 5/40; that is R’ = 8Ω.
Similarly,
1/ R” = 1/30 + 1/20 + 1/60 = 6/60; that is, R” = 10 Ω.
Thus, the total resistance,
R= R’+ R”= 18Ω
To calculate the current, we use Ohm’s law, and get
I =V/R= 12V/18Ω = 0.67A.

Question 49.
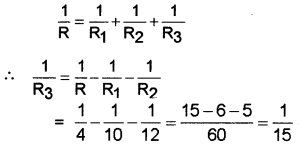
Three resistors are connected In parallel with the 30 V battery. The electric current of 7.5 A flows through circuit from battery. If the values of two resistors are 10 Ω and 12 Ω, determine the value of the third resistor.
Answer:
V = 30 V, 1= 7.5 A, R₁= 10Ω, R₂ = 12Ω, R₃ = ?
The equivalent resistance of circuit R =\(\frac{\mathrm{V}}{\mathrm{l}}=\frac{30}{7.5}!\) = 4Ω
Now, R₁, R₂ and R₃ are connected in parallel.
∴ R₃ = 15Ω

Question 50.
Find the electric current ¡n the following circuit:
Answer:
(A) Here, resistance R₁ is connected in parallel where as R₂ and R₃ are connected in series
Equivalent resistance of R₂ and R₃ is, R’ = R₂ + R₃ = 30 + 30 = 60Ω
Now R₁ and R’ are connected in parallel and so their equivalent resistance is, \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R^{\prime}}\)
∴ \(R=\frac{R_1 \times R^{\prime}}{R_1+R^{\prime}}=\frac{30 \times 60}{30+60}=\frac{1800}{90}=20 \Omega\)

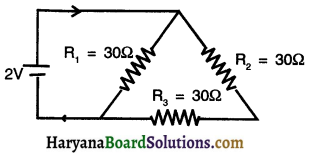
(B) Total current flowing in the circuit \(I=\frac{V}{R}=\frac{2}{20}=0.1 \mathrm{~A}\)

Question 51.
State advantages and disadvantages of a series connection.
Answer:
Advantages of series connection:

• Series connection of resistors helps to control the current in the circuit.
• The fuse is connected in series with AC mains as well as with the electrical appliance. Thus, when a short circuit occurs in any electrical appliance, the fuse wire melts and stops electric current. Thus, senes connection prevents damage to electrical appliances.

Disadvantages of series connection:

• In series connection, the voltage gets divided. Due to this, the appliances give less output.
• If fault occurs in one appliance or at one part of the circuit, the current stops flowing in the entire circuit and other appliances also stop working.

Question 52.
State advantages and disadvantages of a parallel connection.
Answer:
Advantages of parallel connection:

• Voltage drop does not occur in parallel connection. As a result, appliances operate with full efficiency.
• If more than one appliances are connected in parallel and if an appliance stops working, even then the circuit will not break, and the other appliances will keep on working efficiently.
• The equivalent resistance in the parallel connection of resistor decreases, hence more current can be obtained.

Disadvantages of a parallel connection:

• In parallel connection, total resistance R of the circuit decreases, so total current increases. Hence, the current flow cannot be controlled.
• Bulbs having different voltages lets say 220 V, and 240 V, when connect in parallel and given voltage lets say 220 V, then only that bulb which has voltage rating of 220 V will light up with full efficiency.

Question 53.
Differentiate between series connection of resistors and parallel connection of resistors.
Answer:

Series Connection	Parallel Connection
When two or more resistors are connected end to end consecutively, such a connection is called a series connection.	When two or more resistances are connected between the same two points, they are said to be connected in parallel (because they become parallel to each other).
In series connection, the resistors are connected across two points say A and B of the circuit in such a way that equal amount of current flows through each resistor and the current flows in only one path.	In parallel connection, the resistors are connected across two points say A and B of the circuit in such a way that equal amount of voltage drops across two ends of each resistor and the current flows in more than one path.
In this connection, equal amount of current (I) flows through each resistors but voltage (V) of the battery gets divided among the three resistors.	In parallel connection, voltage drop (V) across two ends of each resistor remains same but the current (I) that flows in the circuit gets divided into three parts at point A.
Here, equivalent resistance R = R1+R2+R3	Here, equivalent resistance \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\)
The magnitude of equivalent resistance R is always larger than the largest resistance of the circuit.	The magnitude of equivalent resistance l is always smaller than the smallest resistance.

Question 54.
Differentiate between resistance and resistivity.
Answer:

Resistance	Resistivity
Resistance is the ratio of the voltage applied between the two ends of a conductor to the electric current flowing through the conductor. Thus, R=\(\frac{\mathrm{V}}{\mathrm{l}}\)	Resistivity of a substance is the resistance offered by a conducting wire of unit length and unit cross-section area. Thus, \(\left(\rho=\frac{R \cdot A}{I}\right)\)
Resistance depends on various factors such as type of substance, temperature, pressure, cross-section area, etc.	It depends on type of substance, temperature of the conductor and pressure exerted on conductor.
Its SI unit is OhmΩ	Its SI unit is ohm-meter Ωm.

Question 55.
What is heating effect of electric current?
Answer:
1. When electric current is passed through a high resistance wire, the resistance wire becomes hot and produces heat.
2. Here, electrical energy ¡s converted into heat energy which is known as the heating effect of electric current.
3. The heat produced in an electrical appliance depends on electric current and resistance.

Question 56.
Explain electrical energy and derive its formula. OR Obtain the equation of heat energy for current flowing through a resistor for a specific time period.
Answer:
1. Suppose electric current is flowing through some resistor (R).
2. This results in continuous production of electric charges (Q).
3. The work done (W) by the battery of voit (V) for keeping the electric charges (Q) in continuous flow is,
W = V x Q
∴ W = V x I x t ( ∵ Q = I x t as per the definition of electric current)
Also, as per Ohm’s law, V = I. R
∴ W = l.R x lt = I²Rt
4. Thus, current flowing through a resistor R for time t is I.
5. W is the electrical energy consumed when current I flows through a resistor R in the circuit for time t.
6. This electrical energy gets converted into heat energy.
Thus, heat energy (H) = I² Rt
7. This equation is also called Joule’s law of heating.
8. The SI unit of electrical energy (W) or say heat energy (H) is joule (J).
9. The other units are Watt second (Ws) as well as Kilowatt – hour (kWh) or simply unit.

Question 57.
100 J of heat is produced each second in a 4Ω resistance. Find the potential difference across the resistor.
Answer:
H=100J, R=4Ω, t=1 s, V=?
We have the current through the resistor as

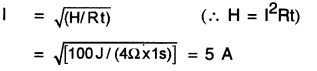
Thus the potential difference across the resistor, V is
V =IR
=5A x 4Ω
= 20V.

Question 58.
5A current flows through an electric Iron. If the resistance of electric iron is 44Ω then how much energy will be consumed in 5 minutes?
Answer:
l = 5A; R = 44Ω,t = 5min =5 x 60 = 300s.
Electricalenergy w = l²Rt
= (5)²(44) (300) = 330000 = x 10⁵ J

Question 59.
Discuss some practical applications of heating effect of electric current.
Answer:
Practical (daily life) applications of heating effect of electric current:
(i) Household heating appliances: Electric iron, toaster, sandwich maker, room heater, electric kettle, etc. ail such appliances make use of heating effect of electric current.

(ii) Electric bulbs: When electricity s passed through the filament of the electric bulbs, the bulbs light up. Here, heating effect is used for emitting light.

(iii) Electric fuse: Electric fuse is a safety device which works on the heating effect of electric current.

Question 60.
How is the heating effect of electric current used to light an electric bulb? Explain.
Answer:
1. The incandescent lamp or electric bulb is a glass which is filled with inactive nitrogen and argon gas.
2. A strong metal such as tungsten which has a very high melting point of 33800 C is used for making the filaments of these bulbs.
3. On passing electric current the filament becomes hot and emits light.

Question 61.
What is a fuse? How does the heating effect of electric current works on fuse? OR How does the fuse work?
Answer:
Fuse:

• A fuse is a safety device which works on the heating effect of electric current. It is connected in series with the device.
• It consists of a piece of wire made of metal or alloy having appropriate melting point.
• If the current larger than the specified amount flows through the circuit, the fuse wire becomes hot. This melts the fuse wire and the circuit gets broken. The connected device does not get electric supply and so it gets safeguarded against over-supply of electricity.
• Fuse for domestic purposes have rating of lA, 2A, 3A, 5A, 10A, etc.

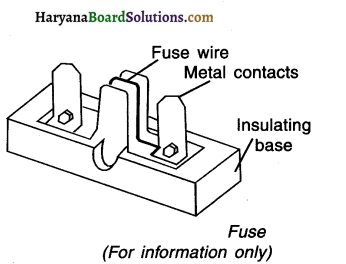
Question 62.
Define electric power and state and explain its unit.
Answer:
Electric power:
1. The electrical energy consumed (or heat energy generated) in unit time ¡s called electric power.
2. In other words, electric power is the rate of electric energy.
3. It is denoted by R

4. The SI unit of power is joule/second or watt (W).

1 Unit power:

• If 1A current flows through the circuit through a battery of 1V, the power consumed will be 1 W.
• We have, P = IV
  ∴ 1 watt = 1 voIt x 1 ampere = 1 VA

Question 63.
Explain the practical unit of electrical energy. What do you mean by 1 unit power?
Answer:
1. \(\text { Power } P=\frac{\text { electric energy }(\mathrm{W})}{\text { time.(t) }}\)
∴ Electrical energy (W) = Power (P) x time (t) watt x second = joule
2. Thus, the unit of electrical energy is watt. second.
3. The larger unit of electrical energy is kWh.
1 kWh = 1000 watt x 3600 seconds
= 3.6 x 10⁶ watt.seconds
= 3.6 x 10⁶ joules (J)
4. kWh is a practical unit of energy which is used in every day life.
5. It is also called a ‘unit’.
6. Thus, 1 unit 1kWh = 3.6 x 10⁶ joules.
7. When a 1000 W bulb is on for 1 hour, the energy consumed is equal to 1 unit.

Question 64.
An electric iron consumes energy at a rate of 840 W when heating is at the maximum rate and 360 W when the heating is at the minimum. The voltage is 220 V. What are the current and the resistance in each case?
Answer:
We know that the power input is P = Vl
Thus, the current I = P/v
(a) When heating is at the maximum rate,
I = 840 W/220 V = 3.82 A; and the resistance of the electric iron is R = V/I = 220 V/3.82 A = 57.60 .

(b) When heating is at the minimum rate,
1= 360 W/220 V= 164 A; and the resistance of the electric iron is
R= V/l= 220 V/1 .64 A= 134.15Ω

Question 65.
An electric bulb is connected to a 220 V generator. The current is 0.50 A. What is the power of the bulb?
Answer:
P =Vl=220V x 0.50A=110 J/S=110 W.

Question 66.
An electric refrigerator rated 400 W operates 8 hour/day. What is the cost of the energy to operate it for 30 days at Rs 3.00 per kWh?
Answer:
The total energy consumed by the refrigerator in 30 days would be
400 W x 8.0 hour/day x 30 days = 96000 Wh = 96 kWh
Thus the cost of energy to operate the refrigerator for 30 days is
96 kWh x ₹ 3.00 per kWh = ₹ 288.00

Question 67.
In a house, if three bulbs of 100 W, 60 W and 30 W are used 2 hours per day, how many units of electrical energy will be consumed in 30 days?
Answer:
Energy consumed per sec P = 100 W + 60 W + 40 W= \(\frac{100}{200}\) W = kWh
P = 0.2 kWh
∴ Energy consumed per day = P x t = 0.2 kWh x 2 = 0.4 kWh
∴ Energy consumed in 30 days = 0.4 x 30 = 12 kWh
Now 1 unit = 1 kWh
∴ Energy consumed in 30 days = 12 units

Question 68.
For the circuit shown in figure below, determine the equivalent resistance between A and B. Also find the current flowing from the battery.

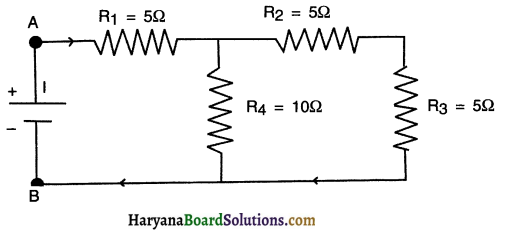
Answer:
As shown in the figure (part-a), R₂ and R₃ are connected in series. Their equivalent resistance
R’ =R₂+R₃=5+5=10Ω
Now R’ is parallel with R₄ (Figure Part b) equivalent resistance,

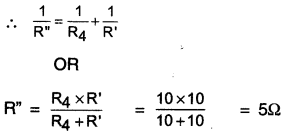
Now R” and R₁ are connected in series (Figure Part c). equivalent resistor across A and B,

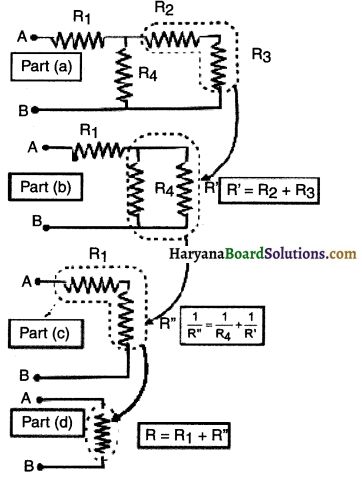
∴ R =R”+R₁
= 5+5
= 10Ω
The current flowing from the battery,
\(I=\frac{V}{R}=\frac{10 V}{10 \Omega}=1 \mathrm{~A}\)

Question 69.
As shown in the figure the resistance are connected with a 12 V battery. Determine (a) Equivalent circuit resistance (b) Current flowing through the circuit.
(A) To determine equivalent resistance of the circuit, we fill first obtain :
(i) Equivalent resistance of R₁ and R₂ which are connected in parallel and
(ii) Equivalent resistance of R₃, R₄ and R₅
Answer:

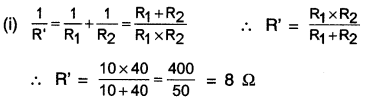
(ii) Equivalent resistance of R₃, R₄ and R₅
\(\frac{1}{R^{\prime \prime}}=\frac{1}{R_3}+\frac{1}{R_4}+\frac{1}{R_5}=\frac{1}{30}+\frac{1}{20}+\frac{1}{60}=\frac{1}{10}\)
∴ R=\(\frac{10}{1}\) = 10Ω
Now, R’ and R” are connected in series and so equivalent resistance
R =R’+R”=8+10=18Ω
Thus, the equivalent resistance of the entire circuit is 18Ω

(C) Current flowing through the circuit
\(I=\frac{V}{R}=\frac{12}{18}\) = 0.66 A
Thus, 0.66 A current flows in the circuit.

Question 70.
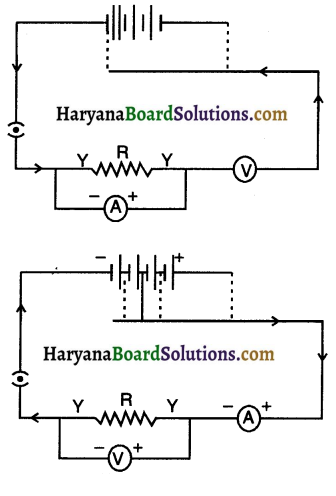
A child has drawn the electric circuit to study Ohm’s law as shown in the figure here. His teacher told that the circuit diagram needs correction. Study the circuit diagram and redraw it after making all corrections.
Answer:
The circuit diagram given in the question has three errors. They are:
(i) Ammeter is connected in parallel with R and voltmeter connected in series. In reality, ammeter should be connected in series and voltmeter in parallel.
(ii) The current is drawn from negative terminal and enters the battery through positive which
(iii) Cells are not connected in series combination in the battery of the circuit.
The correct diagram is figure 12.31.

Question 71.
Three 2Ω resistors’, A, B and C, are connected as shown in the figure. Each of them dissipates energy and can withstand a maximum power of 18W without melting. Find the maximum current that can flow through the three resistors.
Answer:
Resistance, R = 2Ω
Maximum power, P_max = 18W
Maximum current, I_max =?
We know that P = I²R
\(I=\sqrt{\frac{P}{R}}=\sqrt{\frac{18}{2}}=3 A=I_{\max }\)

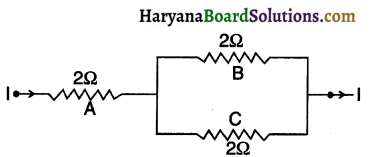
Maximum current that can flow through 2Ω resistor is 3A. This current divides along B and C because in parallel combination, voltage across B and C remain same and so,\(I \propto \frac{1}{R}\)
Since, B and C have same resistance i.e. 2Ω each, same current i.e., \(\frac{3}{2}\) = 1.5 A flows through B as well as C.

Question 72.
What is electrical resistivity? in a series electrical circuit comprising a resistor made up of a metallic wire, the ammeter reads 5 A. The reading of the ammeter decreases to half when the length of the wire is doubled. Why?
Answer:
Resistivity: The property of a material to resist the flow of electric current is called its resistivity. It is denoted as ρ. The SI unity of resistivity is Ωm
The resistance of a uniform conductor is:
\(R=\rho \frac{1}{A}\)
Where,
I = the length of the conductor
ρ = the electrical resistivity of the material
A = the cross-sectional area
Now, if I is doubled, then R also gets doubled.

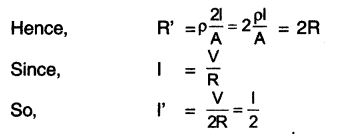
When, R is doubled, I becomes \(\frac{1}{2}\)

Question 73.
B₁, B₂ and B₃ are three identical bulbs connected as shown in Figure. When all the. three bulbs glow, a current of 3A is recorded by the ammeter A.
Answer:
(i) What happens to the glow of the other two bulbs when the bulb B₁ gets fused?
(ii) What happens to the reading of A₁, A₂, A₃ and A when the bulb B₂ gets fused?
(iii) How much power is dissipated in the circuit when all the three bulbs glow together?
Resistance of combination of three bulbs in parallel

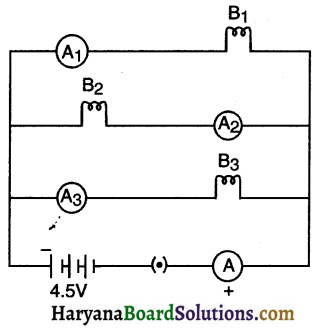
(i) When bulb B₁ gets fused, the currents in B₂ and B₃ remain same. This means, I₂ = I₃ = 1A. The reason for this is that the voltage across the B₂ and B₃ bulb remains same. As a result, they keep illuminating with same intensity as before.

(ii) When bulb B₂ gets fused, the current in B₂ becomes zero and current in B₁ and B₃ remains 1 A. The reason for this is that the voltage across blub B₁ and B₃ remain same.
Total current I = 1 + 12 + 13 = 1 + 0 + 1 = 2A
Current in ammeter A₂ = 0 Current in ammeter A₁ = 1A
Current in ammeter A₃ = 1A Current in ammeter A = 2A

(iii) When all the three bulbs are connected.
Power dissipated, \(P=\frac{V^2}{R_{e q}}=\frac{(4.5)^2}{1.5}=13.5 \mathrm{~W}\)

Question 74.
A given length of a wire is doubled on itself and this process is repeated once again. By what factor does the resistance of the wire change?
Answer:

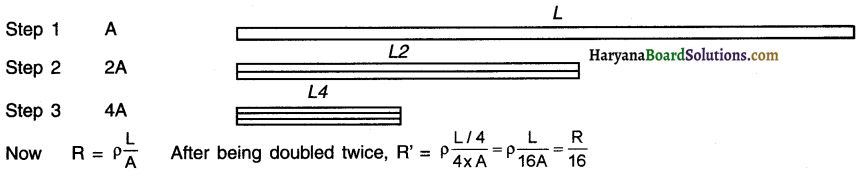
Question 75.
A wire of length I and area of cross-section A was drawn Into a wire of double its length by melting It. If Its original resistivity and resistance were p and R respectively, what will be its new resistivity and resistance?
Answer:
The volume of the wire remains same in both cases.
Volume = Area of cross-section x Length

Thus, the resistivity ρ remains the same.

Question 76.
A household uses the following electric appliances:
(i) Refrigerator of rating 400 W for two hours each day.
(ii) Two electrIc fans of rating 80 W each for twelve hours each day.
(iii) Six electric tubes of rating 18 W each for 6 hours each day.
Calculate the electricity bill of the household for the month of June if the cost per unit of electric energy is 3.00.
Answer:
1. Energy consumed by refrigerator of rating 400 W for ten hours each day
= P x t = 400W x 2h =\(\frac{400}{1000}\) kW x 2h = 0.8kWh

2. Energy consumed by two electric fans of rating 80 W each for twelve hours each day
= 2 x P x t = 2×80 W x 12 h = \(\frac{160}{1000}\) kW x 12 h = 1.92 kWh

3. Energy consumed by six electric tubes of rating 18 W each for six hours each day
=6 x P x t = 6 x 18 W x 6h = \(\frac{108}{1000}\) W x 6h = 0.648 kWh

4. Total energy consumed in the month of June (30 days)
= (0.8 + 1.92 + 0.648) x 30 kWh
= 6.568 x 30 = 197.04 kWh

5. Electricity bill for the month of June
= ₹ 197.04 x 3 = ₹ 591.12 = ₹ 591 (approx)

Very Short Answer Type Question :

Question 1.
What is electric charge? State Its types.
Answer:
Electric charge is the basic property of a matter carried by some elementary particles. The charge can be of two types namely positive charge and negative charge.

Question 2.
State the basic difference between static electricity and current electricity.
Answer:
Static electricity refers to the physical effect caused by the stationery charges whereas current electricity refers to physical effect caused by the moving charges.

Question 3.
What is conventional current? State the direction of flow of conventional current.
Answer:
The existence of electric current due to the flow of positive charges is known as conventional current. The direction of flow of conventional current is from the positive terminal to the negative terminal of a battery.

Question 4.
What is an open circuit?
Answer:
An electric circuit through which no current flows is called an open circuit.

Question 5.
What is a closed circuit?
Answer:
An electric circuit through which current flows continuously is called a closed circuit.

Question 6.
What is the function of an ammeter? How should it be connected in a circuit?
Answer:
Ammeter is used to measure the electric current in a circuit. It should be connected n series with the circuit.

Question 7.
Should the resistance of an ammeter be low or high? Give reason.
Answer:
Ammeter is used to measure the current and is connected in series with the circuit. If, ammeter has a high resistance, it will reduce the current flowing through the circuit and give an inaccurate result of measure of electric current. Hence, ammeter should have as low resistance as possible.

Question 8.
A charge of 900 C flows through a cross section of a conductor for 5 minutes. Calculate the electric current drawn by the conductor.
Answer:
Q = 900 t = 5 (mEnutes) x 60 (second) = 300 s
We know that \(I=\frac{Q}{t}\) ∴ \(I=\frac{900}{300}=3 A\)
Thus, electric current drawn by this circuit is 3 A.

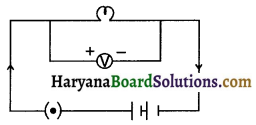
Question 9.
Provided here is an electric circuit consisting of a bulb, battery and a key. I want to measure the potential difference potential difference between the two terminals of the bulb. Redraw the circuit by adding required device which can measure the potential difference.

Answer:

Question 10.
How much amount of charge can be moved from point to B If the work of 12 joule is done with the potential difference of 4 volt between these two points?
Answer:
W = 12J V = 4V
We know that V Volt \(=\frac{\mathrm{W}(\text { Joule })}{\mathrm{Q}(\text { Coulomb })}\)
∴ \(4=\frac{12}{Q}\)
∴ Q = 3C
Thus, 3C of charge can be moved from point A to B if work of 12 joule is done with potential difference of 4 volt between these points.

Question 11.
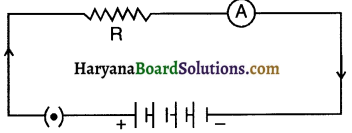
Heena Madam asked Rohit to draw a circuit containing Resister ‘R’ connected with a battery along with an ammeter to measure the current flowing through R. Rohit has drawn the circuit provided here and it has some errors in it. Rectify and redraw the circuit.

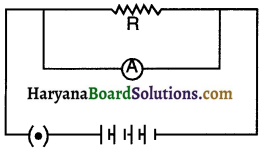
Answer:

Question 12.
Match the following components with their correct symbols.

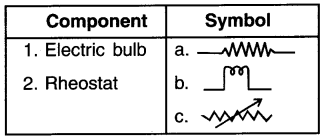
Answer:
(1-b), (2-c)

Question 13.
Point out the errors in the circuit drawn below which measures the volt across resistor R.

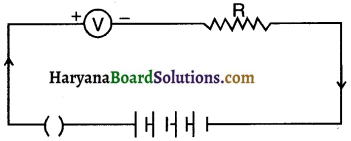
Error 1 : Voltmeter is connected in series. It should be connected in parallel in order to measure the voltage.
Error 2 : The key is open. Hence the electric current cannot flow. It should be closed.

Question 14.
Two students perform experiments on two given resistors R₁ and R₂ and plot the V-l graphs as shown in diagram 1 and 2 respectively. If R₁> R₂, which of two diagrams correctly represent the situation on the plotted curves? Justify your answer.

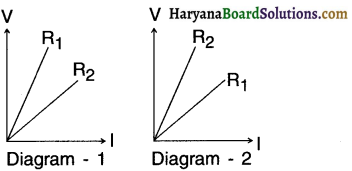
Resistance is the slope of graph V-l. The graph with higher slope indicates that the resistance for that particular graph is higher. We can see from diagram 1 that R₁> R₂ hence diagram 1 correctly represents the situation.

Question 15.
What is the relationship between the potential coefficient and electric current flowing through a conductor in a circuit Who kind out this relation?
Answer:
The potential difference across a conductor is directly proportional to the electric current flowing through it in a circuit. This relation was found out by German physicist George Simon Ohm.

Question 16.
Calculate the potential difference of the battery in circuit provided here.
Answer:
l = 2.5mA = 2.5 x 10^-3A, R = 20 KΩ
= 20 x 10³ Ω
We know that V = IR
∴ V = (2.5 x 10^-3A) x (20 x 10³Ω) = 50V
Thus, the battery connected in this circuit has a voltage rating of 50 V.

Question 17.
What is the nature of a graph plotted with electric current at X-axis and potential difference at Y-axis?
Answer:
The graph plotted with electric current at X-axis and potential difference at Y-axis is a straight line passing through origin.

Question 18.
In an electric circuit, what change in electric current can we observe if we double the resistance keeping potential difference constant?
Answer:
1. Suppose, initially current and resistance of the circuit is I₁ α R₂ respectively.
2. After the resistance is doubled, current and resistance are I₂ and R₂ (R₂ = 2R₁)

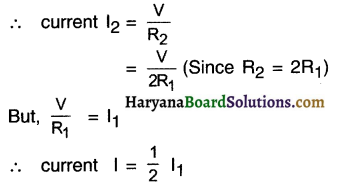
Hence, if we double the resistance, current gets halved.

Question 19.
What is the relation between the resistance of a conductor and electric current flowing through it?
Answer:
In an electric circuit, the current is inversely proportional to the resistance of the conductor.

Question 20.
Classify below provided materials as (1) Good conductor, (2) Resistor, (3) Poor conductor and (4) Insulator.
Nichrome, Drinking water, Tungsten, Diamond.
Answer:
Good conductor: Tungsten, Resistor: Nichrome,
Poor conductor: Drinking water, Insulator: Diamond

Question 21.
On which factors does the resistance of a conductor depend?
Answer:
Resistance of a conductor depends on:

• Cross-sectional area,
• Length,
• Nature of material.

Question 22.
What is the relation of resistance with length and cross-sectional area of a conductor?
Answer:
Resistance is directly proportional to the length and inversely proportional to the area of cross-section of a conductor.

Question 23.
Choose the combination with highest resistance.
(a) A wire of length 2m and cross sectional area 2m²
(b) A wire of length 4m and cross sectional area of 2m²
(c) A wire of length 2m and cross sectional area 4m²
(d) A wire of length 4m and cross sectional area of 4m²
Answer:
The combination with a wire of length 4m and cross sectional area of 2m² will provide maximum resistance.

Question 24.
A wire of resistivity ρ is stretched to three times its length. What will be Its new resistivity?
Answer:
The resistivity of a material depends on the nature of the material of the wire and not its dimensions. Hence, the resistivity p will remain unchanged even if it is stretched three times.

Question 25.
Based on the resistivity of three distinct materials provided here, classify the materials Into conductors, alloys and insulators:
(a) 100 x 10^-6
(b) 1.84 x 10^-6
(c) 1.36 x 10^-10
Answer:
(a)-Alloy, (b)-Conductor, (c)-lnsulator

Question 26.
What happens to the resistance of a conductor. when its area of cross-section ¡s increased?
Answer:
\(R \propto \frac{1}{A}\) So, as the area of cross-section is increases, the resistance decreases.

Question 27.
The following table gives the resistivity of three samples:

Which of these is suitable for making heating elements of electrical appliances and why?
Answer:
Sample C has highest resistivity. Hence, it is most suitable for making heating elements of electrical appliances.

Question 28.
Haresh has purchased a coil of nichrome for his school project. He wants to cut out a segment from this coil such that resistance of the segment is 2 ohm. If the cross-sectional area of this coil is 3.14 x 10 m² and the resistivity of nichrome Is 100 x 10 ohm m, what should be the length of segment that Haresh needs to cut from coil?
Answer:
R=2Ω
A =3.14 x 10^-6 m²
ρ =100 x 10^-6  Ωm
I  = ?

Question 29.
Two wires of equal length, one of copper and the other of nichrome have the same resistance. Which wire will be thicker?
Answer:
Nichrome wire is thicker than copper wire.

Question 30.
Arrange the below-mentioned metals In order such that the metal with lowest conductivity comes first and the one with highest conductivity comes last.
(a) Copper
(b) Mercury
(c) Silver
(d) Iron
Answer:
(c), (a), (d), (b)

Question 31.
Which are the methods of joining resistors In a circuit?
Answer:
There are two combination of joining resistors in a circuit. They are
(1) Series connection and
(2) Parallel connection

Question 32.
Name the physical quantities which remain same in all the resistors when (i) they are connected In series, (ii) they are connected In parallel.
Answer:
(i) When the resistors are connected in series, the electric current is same for all the resistors.
(ii) When the resistors are connected in parallel, the voltage across each of the resistors is same.

Question 33.
Calculate the equivalent resistance in the combination of resistance shown here.

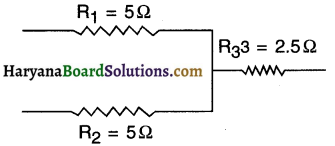
Answer:
Here, R₁ and R₂ are connected in parallel connection and R₃ is in series.
∴ equivalent resistance \(R=\frac{R_1 R_2}{R_1+R_2}+R_3\)
∴ R = \(\frac{5 \times 5}{5+5}\)+2.5=2.5+2.5 R =5Ω

Question 34.
Calculate the voltage of battery connected in circuit provided here.

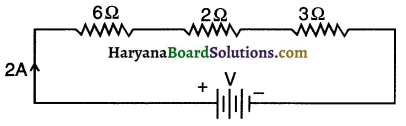
Answer:
We know that V = IR
∴ V = 2A x (6+2+3)Ω
V = 22V

Question 35.
Draw a schematic diagram of an electric circuit comprising of 3 cells, a parallel combination of two bulbs and plug key in the ON mode connected with an ammeter and a voltmeter.
Answer:

Question 36.
Two resistors are connected in a parallel combination such that the equivalent resistance s 1 ohm. If one of the resistors has a value of 2 ohm, calculate the value for the other resistor.
Answer:
We know that for parallel combination,
\(R=\frac{R_1 R_2}{R_1+R_2}\)
(But equivalent resistance = 1Ω and R₁ = 2Ω)
∴ \(1=\frac{2 R_2}{2+R_2}\)
∴ 2+R₂=2R₂
∴ R₂ = 2Ω

Question 37.
Out of the two wires X and Y shown below, which one has greater resistance? Justify.

Answer:
The resistance is directly proportional to the length of the wire. Now we can see that wire Y is longer than X and hence it will offer higher resistance.

Question 38.
What would be the equivalent resistance of a parallel combination of resistors made by cutting a wire of resistor R in three equal parts. What will be the effect on resistivity of each of the segments?
Answer:
Resistance of wire (with resistance R) when cut in 3 equal parts would have resistance R/3 for each segment.
Let’s say resistances are r₁, r₂ and r₃
∴ equivalent resistance = \(\frac{r_1 r_2 r_3}{r_1+r_2+r_3}\)
But, r₁ = r₂ = r₃ = R/3
∴ equivalent resistance \(=\frac{\frac{\mathrm{R}^3}{27}}{\mathrm{R}}\)
∴ equivalent resistance \(=\frac{\mathrm{R}^2}{27}\)
Resistivity of the segments will remain the same as it was in the wire before cutting it because resistivity does not depend on the length of material.

Question 39.
Why do we use copper and aluminium wires for transmission of electric current?
Answer:
Because both copper and aluminium have low resistivity and hence high conductivity

Question 40.
Which one is having lesser resistance? A 220 V, 60 W bulb or a 220 V, 40 W bulb?
Answer:
1.  We know that P = V²/R
∴ R=V²/P
2. Now, Voltage applied is same for both the bulbs, hence relative value of resistances of both the bulbs are dependent on the value of powers.
Now, R α 1/P
Therefore, more the power less the resistance.
Hence, the bulb with 60W rating will have lesser resistance than the bulb with 40W rating.

Question 41.
Give one reason which justifies that parallel circuits are preferred in domestic wiring.
Answer:
In parallel circuit, if one device gets damaged and stops working, there is no effect in the functioning of other connected devices. Hence, parallel circuits are preferred in domestic wiring.

Question 42.
Write relation between heat energy produced In a conductor when a potential difference V is applied across its terminals and a current I flows through in time t. What is this relation known as?
Answer:
Heat energy can be expressed as H = Vit. This is also known as Joule’s law of heating

Question 43.
State the relationship between 1 Volt and 1 Joule.
Answer:
1 Volt \(=\frac{\text { 1Joule }}{1 \text { Coulomb }} \text { or } 1 \mathrm{~V}=\frac{1 \mathrm{~J}}{1 \mathrm{C}}\)

Question 44.
As per the Joule’s law of heating, on which parameters does the heat produced In a resistor depend?
Answer:
The heat produced in a resistor is directly proportional to (a) square of current, (b) resistance and (c) time for which the current flows through resistor.

Question 45.
State the difference between the wire used In the element of an electric heater and in a fuse wire.
Answer:
Wire used in electric heater should have a high resistivity and high melting point allowing the wire to produce heat without melting down where as a fuse wire should have a low resistance and low melting point so that it can protect the appliance connected with it due to fluctuating current.

Question 46.
List two characteristics of the material used in electric heating devices.
Answer:
Material used in heater wire should have

• High Resistivity and
• High melting point.

Question 47.
An electric iron draws a current of 3.5 A when connected with a voltage source of 220V. Calculate the energy consumed by iron if it is kept on for 2 hour.
Answer:
I = 3.5A
V = 220V
t = 2hr
energy consumed E =?
We know that E = Vit
=220 x 3.5 x 2
=1540 Wh
∴ E= 1.54 kWh

Question 48.
Why do we use tungsten for making bulb filaments?
Answer:
The filament in bulb should have the capacity to retain extremely hot temperature so that it can emit light. As tungsten has a very high melting point (3380°C). It can retain heat without melting down and so it is used for making bulb filaments.

Question 49.
How does use of a fuse wire protect electrical appliance?
Answer:
Fuse wire has a very low melting point. A fuse is connected in series with the appliance. Hence if more than an acceptable amount of current flows in the circuit, the fuse wire melts down due to heating effect and breaks the circuit. This helps
in protecting the appliance against the damage caused by fluctuating current.

Question 50.
Melting points of three metals are provided here: (a) 3380 °C, (b) 1085 °C, (c) 232°C. Which of these metal can be used to produce a fuse wire, a bulb and an electric transmission line.
Answer:
Metal with melting point 3380°C, should be used for producing bulb, metal with melting point 1085 °C should be used for producing electrictransmission line and the metal with melting point 232 °C should be used for producing fuse wire.

Question 51.
400 J of heat is produced in 4s in a 4Ω resistor. Find potential difference across the resistor.
Answer:
H = 400J, t = 4s and R = 4Ω.
We know that,
H=I²Rt
∴ I²=H/Rt
∴ I =5A
We Also know that,
H = V/t
∴ V=H/It
∴ V = 20V

Question 52.
How much electric energy can be consumed by a 150W toaster in lo minutes?
Answer:
P = 150 W, t = 10 minutes = 10 x 60 seconds
= 600 seconds
We know that electric energy E = Pt
∴ E = 150 x 600 = 90,000 J
∴ E =90 x 10³ J

Question 53.
Can a fuse wire of capacity 3A protect a circuit consuming 1 kW electric power when connected with a voltage source of 220V?
Answer:
The electric circuit that has a 1 kW power at 220 V will draw electric current I = P/V
∴ \(I=\frac{1000}{220}\) = 4.54 A
Hence, the fuse wire of 3A current rating cannot protect this circuit as it will require a fuse wire of More than, 4.54 A rating.

Question 54.
What is the commercial unit of electrical energy? Represent it in terms of joules. Commercial unit of energy is kW h. It can be represented in Joules as follows:
Answer:
1 Kilowatt hour = 1000 watt hour
We know that 1 watt = 1 joule / seconds
∴ 1 kWh = \(\frac{1000 \text { joule }}{\text { second }}\) x 3600 (second) second
∴ 1 kWh = 3.6 x 10⁶ joules

Question 55.
An electric device operates at 24 V and has a resistance of 8Ω. Calculate the power consumed by the device and current flowing through it.
Answer:
Voltage = 24V and R = 8Ω
We know that I = V/R
∴ I = 3A
And, P=Vl
∴ P = 24 x 3
∴ P = 72W

Question 56.
An electric current of 5.0 A flows through a 12Ω resistor. What is the rate at which heat energy is produced in the resistor?
Answer:
l = 5A and R=12Ω
Rate of consumption of energy is the power and
we know that,
P = I²R
∴ P=(5)² x 12
∴ P = 300W

Fill in the blanks:

1. …………………. is expressed by the amount of charge flowing through a particular area in unit time.
Answer: Electric current

2. Coulomb charge constitute electrons.
Answer:  6 x 10¹⁸

3. In ………………… combination of resistance, the magnitude of equivalent resistance is greater than the largest resistance.
Answer: Series

4. The work done on the electric charge to maintain its equilibrium with the other charge is called ………………
Answer: Electric potential

5. A/An ………………. (instrument) measures electric current in a circuit whereas a/an (instrument) is used to measure the potential difference.
Answer: ammeter, voltmeter

6. Chemical reaction within a cell is responsible for generating ……………………. across its terminals.
Answer:  potential difference

7. A device called ………………… is used to change electric current flowing in a circuit by keeping potential difference constant.
Answer: rheostat

8. Joule/Coulomb is the SI unit for ………………………
Answer:  potential difference

9. Voltmeter is connected in …………………….. and ammeter is connected in ………………..
Answer: Parallel; Series

10. The graph of potential difference v/s electric current is a and it validates Law.
Answer: straight line, Ohm’s

11. The unit Volt/Ampere can also be represented as and is symbolized as ……………………..
Answer: Ohm

12. If we increase the cross sectional area of a conductor, the amount of current flowing through it ………. whereas the resistance …………………….. .
Answer: increases, decreases

13. The resistance of any conduction substance is …………….. proportional to length of the substance.
Answer: Directly

14. The resistance of a conductor is proportional to area of cross-section of the substance.
Answer: Inversely

15. ………….. is widely used as a filament in electric bulbs.
Answer: Tungsten

16. In a combination of resistance, all the resistors are simultaneously connected together between two points in a circuit, whereas in a combination, resistors are connected end to end consecutively between two points in a circuit.
Answer: parallel, series

17. In an electric circuit, a part of the source energy is consumed in the form of useful work whereas a fraction of this energy gets expended in form of…………………
Answer:  heat

18. Heat produced in a resistor is directly proportional to ………………….., and ……………………..  of electric current flowing through the circuit and also time during which the current flows through circuit.
Answer: resistance, square

19. Devices such as electric iron and electric heater works on the principle of …………… Law.
Answer:  Joule’s

20. A porcelain cartridge encases a ……………… which protects the appliances from fluctuating currents.
Answer: fuse wire

21. 1 kWh =………………….
Answer:  3.6 x 10⁶ joule

22. If you run ……………… watt bulb for 1 hour, the energy consumed will be 1 unit.
Answer: 10³

23. A fuse wire should have relatively …………………… (higher/lower) melting point than the conductor it is connected with.
Answer: lower

24. ………………………………. can be termed as the rate of consumption of energy.
Answer: Power

25. Electric energy consumed is the product of power and …………….
Answer:  time

True OR False:

1. The direction of electric current flowing through a conductor is from the negative terminal to positive terminal of a battery which is opposite to the direction of conventional current. — True
2. The electric current in a circuit gets doubled as we double the length of a conductor through which the current flows. — False
3. 6 x 10¹² electrons flowing through a conductor in one second constitutes one microampere of electric current. — True
4. In a series combination of resistors, equal amount of electric current flows through each resistor whereas, in a parallel circuit, the current gets divided proportionately among each resistors. — True
5. A voltmeter should be connected in a series combination and an ammeter should be connected in a parallel combination with the conductor through which we want to calculate current and voltage. — False
6. The V-l graph provided here is a straight line with constant resistance and it validates the Ohm’s law — False
7. Two resistors of same material with different length and same cross-sectional area will have different resistivity, — False
8. Resistance as well as resistivity of a material are dependent on the temperature of that material. — True
9. Material A has a resistivity of 5.2 x 10^-8 and material B has a resistivity of 49 x 10^-8. In this case, A can be chosen over B to produce electric transmission lines. — True
10. In a series combination of a resistors 1 equal amount of potential difference is observed across each resistor whereas in a parallel combination, potential difference gets divided based on the value each resistor. — False
11. Equivalent resistance in a parallel combination is higher than the highest individual resistance of the resistor connected in circuit. — False
12. Electric bulbs are filled with non-reactive noble gas to prolong the life of filament. — True
13. A large amount of power consumed by an electric bulb is used in emitting light and the remaining amount gets dissipated in the form of heat. — False
14. A fuse wire of 4A current rating is incapable of protecting an appliance with a rating of 5A. — True
15. Fuse wires are always connected in parallel to the circuit because they have very low resistance hence any high fluctuating amount of current would pass through the fuse without harming the appliance connected with it. — False
16. Rate of doing work is the product of voltage applied in the circuit and the current flowing through it. — True
17. 1 kW h is the energy consumed when one Watt of power is utilized for one hour.– False

Match the Following:
Question 1.

Characteristic	Resistivity
1. Insulator	a. 2.6 x 10-8
2. Poor conductor	b. 100 x 10-6
3. Resistor	c. 1.36 x 1010
4. Good conductor	d. 3.4 x 10-2

Answer:
(1-c), (2-d), (3-b), (4-a)

Question 2.

Physical Quantity	Characteristic
1. Resistance	a. Directly proportional to potential difference applied
2. Electric current	b. Dependent on the direction of flow of current
3. Heat in a resistor	c. Directly proportional to square of electric current
4. Power	d. Inversely proportional to cross-sectional area
	e. Product of potential difference and electric current

Answer: (1-c), (2-a), (3-e), (4-d)

Question 3.

Device	Description
1. Rheostat	a. Converts heat energy into light energy
2. Ammeter	b. Protects appliances from fluctuating current
3. Voltmeter	c. Can change current by keeping voltage source constant
4. Fuse	d. Should be connected n parallel to the conductor
	e. Used to measure electric current

Answer:
(1-c),(2-e),(3-d),(4-b)