HBSE 10th Class Science Important Questions Chapter 10 Light Reflection and Refraction

Haryana State Board HBSE 10th Class Science Important Questions Chapter 10 Light Reflection and Refraction Important Questions and Answers.

Haryana Board 10th Class Science Important Questions Chapter 10 Light Reflection and Refraction

Question 1.
What is light? How does it enables us to see things?
Answer:
1. Light consists of electro-magnetic waves. These waves produce sensation in our eyes.
2. When light falls on an object let us say a book, or a table, etc, it gets reflected. The reflected light rays reach our eyes and enable us to see the object.

Question 2.
Discuss the nature of light. OR State the basic properties of light.
Answer:
1. Light waves do not require a material medium (such as solid, liquid or gas) for their propagation and hence are called non-mechanical waves.
2. Light waves travel at a speed of 3 x 10⁸ m/s in vacuum.
3. The speed of light waves depend upon the nature of medium through which they pass.

4. In practical terms, a light wave can travel from one point to another. Such a propagation of light waves in one straightline and from one point to another is known as a ‘ray’. Bundle of such rays is known as ‘beam of light’.
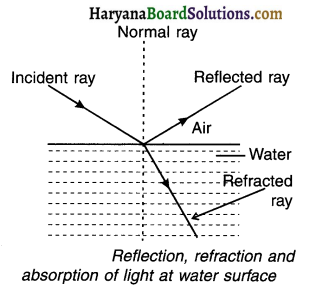
5. When light is incident on a surface separating two’ medias such as air and water, then some part of incident light is reflected, some part is transmitted and some part of it is absorbed by that surface.
6. Light which is incident on a completely polished shining plane surface gets reflected whereas light incident on a transparent medium (such as glass) gets refracted and passes through that medium.
7. Due to these properties of light i.e. reflection and refraction, the light rays can be focused by mirrors and lenses respectively.
8. Moreover, due to reflection and refraction of light, real or virtual images are formed.

Question 3.
What is reflection of light? State its types.
Answer:
Reflection :

• The phenomenon of sending back the light rays which fall on the surface of an object when light is incident on it, is called reflection of light.
• For example, when light falls on a plane mirror, the mirror sends it back i.e. reflects it.

Types of reflection:
(A) Regular reflection and
(B) Irregular reflection

Question 4.
Explain the types of reflection.
Answer:
(A) Regular reflection :
When a parallel beam of light falls on a smooth or shining surface, then the reflected beam is also parallel and directed back in a fixed direction. This type of reflection is known as regular reflection. For example, reflection by a mirror.

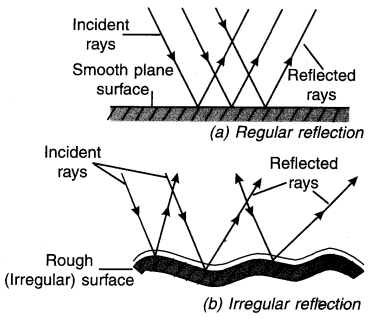
(B) Irregular (diffused) reflection :
When a parallel beam of light falls on a rough surface i.e. irregular surface, the reflected light is not parallel but spreads over a wide area. This type of reflection is known as irregular reflection. For example, light falling on chair, book, etc. gets reflected and helps us to see these objects.

Question 5.
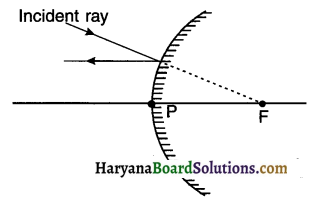
Define incident angle and reflection angle. Also state the laws of reflection.
Answer:
Angle of incidence (θ_i):
The angle that the incident ray makes with normal drawn at the point of incidence is known as incident angle or angle of incidence. It is denoted by θ_i (θ = theta).

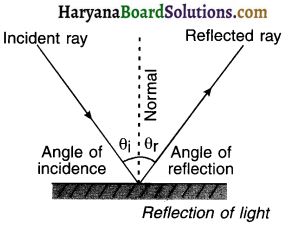
Angle of reflection (θ_r):

The angle that the reflected ray makes with normal drawn at the point of reflection is known as reflection angle or angle of reflection, It is denoted by θ_r

Laws of reflection:
1. The angle of incidence (θi) = the angle of reflection (θr).

2. (a) The incident ray,
(b) the normal to the mirror at the point of incidence and
(c) the reflected ray – all lie in the same plane.

(Note: The laws of reflection are applicable equally to plane as well as spherical mirrors. Moreover they are also applicable to regular as well as irregular surfaces.)

Question 6.
What is an image? Explain the types of images.
Answer:
Image: When a number of rays emerging from a point of an object, after reflection or refraction, ‘meet’ or ‘appear to meet’ at another point, then the point of meeting is called the image of the first point.

Types:
(1) Real image and
(2) Virtual image

(1) Real image: When the rays of light after reflection or refraction ‘actually meet’ at a point, the image formed is called a real image.

• Real image can be obtained on a screen.
• Real image is always inverted. For e.g., image formed on cinema screens.

(2) Virtual image: When the rays of light after reflection or refraction ‘do not actually meet’ but ‘appear to meet’ at a point, the image formed is called a virtual image.

• Virtual image cannot be obtained on a screen.
• Virtual image is always erect. For e.g., our image formed when we stand in front of a mirror is a virtual image.

Question 7.
What is a mirror? State Its types.
Answer:
A polished shining surface which reflects almost all the light incident on it is called a mirror.
Types of mirror:
(1) Plane mirror and
(2) Spherical mirror. Further, spherical mirrors are of two types.

They are:

• Concave mirror and
• Convex mirror.

Question 8.
Discuss the different types of mirrors.
Answer:
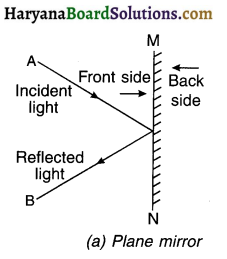
(A) Plane mirror:
1. A plane mirror is a thin, flat and smooth sheet of glass having a shining coat of silver metal on one side.
2. For example, mirror used in vehicles, in dressing tables, etc.
3. When a parallel beam of light rays falls on a plane mirror, it is reflected as a parallel beam.
4. Thus, plane mirror changes only the direction of the incident light rays. It does not converge or diverge them.
(Note: To bring the parallel light rays closer is called converging them where as to spread out is called diverging.)

(B) Spherical mirror:

• Unlike plane mirrors, spherical (curved) mirrors converge or diverge the parallel light rays incident on them.
• A spherical mirror is a mirror whose reflecting surface is in fact a part of a hollow sphere of a glass.
•  When light rays fall on spherical mirrors, they converge or diverge i.e. the incident parallel rays come closer or spread-out unlike plane mirrors where they are just reflected as parallel beams.

Spherical mirrors are of two types :
(i) Concave mirrors and
(ii) Convex mirrors.

Question 9.
Give a brief idea about how a spherical mirror is formed.
Answer:
1. A spherical mirror is a curved mirror (i.e. not a plane mirror).
(Note: Since the spherical mirror is curved, we consider the mirror as cut-out from a sphere. Doing so helps us to understand various terms related to spherical mirrors and image formation through these mirrors.)
2. The simplest spherical mirror is a spoon that we have in our kitchen. The front and back of the spoon behaves like two different types of spherical mirrors giving upward and inverted images.

Types: Spherical mirrors are of two types.

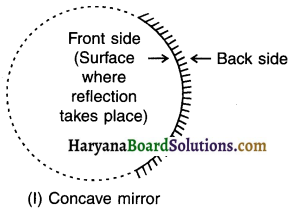
(a) Concave mirror: The spherical mirror in which light rays converge to form an image is called a concave mirror (or converging mirror).

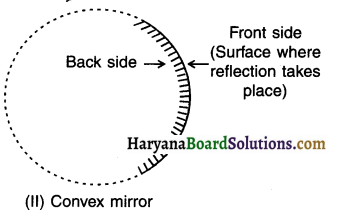
(b) Convex mirror: A spherical mirror in which light rays diverge to form an image is called a convex mirror (or diverging mirror).

Question 10.
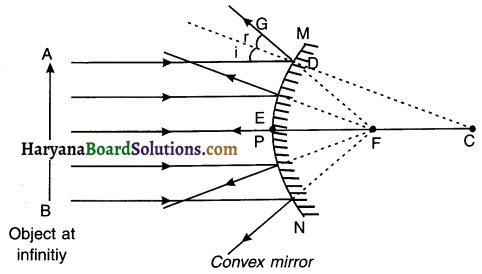
With the help of a suitable diagram define the following terms for concave and convex mirrors (Spherical mirrors).
Answer:
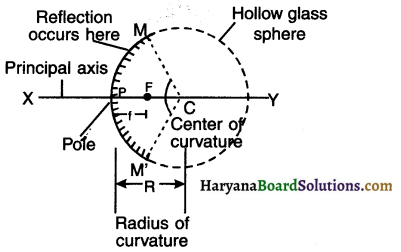
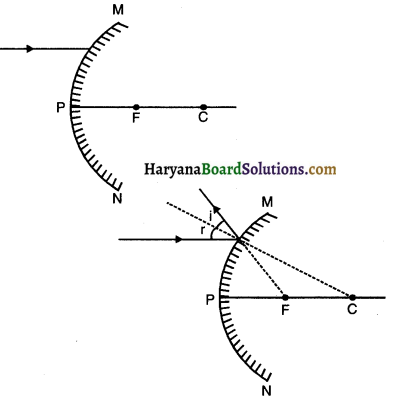
(1) Centre of curvature (C)
(2) Radius of curvature (R)
(3) Pole (P)
(4) Principal axis
(5) Aperture (MN)
(6) Principle focus (F)
(7) Focal length (f)

1. Centre of curvature (C): The centre of spherical sphere from which a mirror is made is known as centre of curvature (C). (Note: Centre of curvature of a concave mirror lies in front where as in convex mirror it lies behind.) Point C is also called 2F since it lies at double the distance of PR

2. Radius of curvature (R): The radius of spherical sphere i.e. from centre of curvature C to pole P i.e. CP from which a mirror is made is known as radius of curvature (R). Thus CP = R. (Note: CP = 2 times PF and so is also written as 2F.)

3. Pole (P): The centre of reflecting surface i.e. MN is known as pole of mirror (P).

4. Principal axis: The imaginary line passing through the pole (P) and centre of curvature (C) is known as principal axis. A

5. Aperture (MN): The portion of the reflecting surface (mirror) from which the reflection of light actually takes place is known as its aperture MN.

6. PrincIple focus (F): The point (F) on the principle axis where the beam of light parallel to the principle axis either actually converges to or diverges from, after reflection from a mirror is called the principle focus (F).

7. Focal length (f): The distance between the pole (P) and principle focus (F) is called focal length (f). Thus, f = PF.

Question 11.
How can you study image formed by a mirror (or a lens)?
Answer:
1. The image of an object formed by a spherical mirror (or a (ens) can be obtained and studied by constructing a ray diagram.
2. Two rays are sufficient to draw a ray diagram because by intersecting two reflected rays we can obtain the position of the image formed.

Question 12.
State the various types of rays that hit a spherical (concave) mirror and direction of their reflecton. Draw ray-diagram to explain how the image will form through these rays.
Answer:
Types of Rays and their Reflection in a Concave Mirror

Question 13.
How do parallel rays converge or diverge in spherical mirrors? Explain with the help of diagrams. OR With necessary diagrams, explain the formation of principal focus and focal length of concave and convex mirrors.
(A) Concave mirror:

• When parallel rays are incident on concave mirror, on reflection, they converge i.e. come closer to each other and meet at a point called principal focus (F). Hence, concave mirror is also called a converging mirror.
• The distance between the pole (P) of the concave mirror and focus (F) is called its focal length (1).
• Note that since all the reflected rays actually pass from the focus (F), a concave mirror has a real focus.
• The focus (F) of concave mirror is in the front of the mirror.

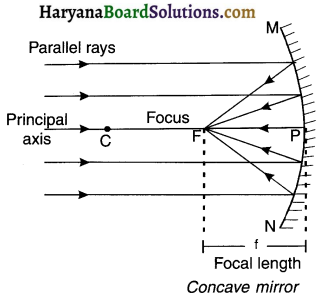
(B) Convex mirror:

• When parallel rays are incident on convex mirror, on reflection, they diverge i.e. spread out from each other. Hence, convex mirror is also called a diverging mirror.
• If you look at the mirror from left side, the reflected (divergent) rays appear to be coming from a point (F) behind the convex mirror.
• The distance between the pole (P) and principal focus (F) is called the focal length (f) of the convex mirror.
• This point F is called the principal focus of the convex mirror.
• Note that since the reflected rays do not actually pass through the focus (F) of the convex mirror, it is said that convex mirror has a virtual (non-real) focus.
• Also note that this virtual focus lies behind the convex mirror.

Question 14.
State and explain the relation between radius of curvature (R) and focal length (f) of a spherical mirror
Answer:
1. For a spherical mirror (both concave and convex), the principal focus (F) lies exactly at the mid-way between pole (P) and center of curvature (C).
2. We know that distance between pole (P) and center of curvature (C) is called the radius of curvature and is denoted by R.
∴ Focal length \((f)=\frac{1}{2} R=\frac{R}{2}\)
Also, R = 2f i.e. radius is twice the focal length (f).

Question 15.
Radius of curvature of a convex minor is 15 cm. Find out its focal length.
Answer:
R = 15cm
F= ?
We know that
Focal length f = \(\frac{\mathrm{R}}{2}\)
∴ F = \(\frac{15}{2}\) = 7.5cm
Thus, focal length of the convex mirror is 7.5 cm.

Question 16.
Focal length of a concave mirror used in a laboratory is 12 cm. What will be the radius of its curvature?
Answer:
Answer:
F = 12cm
R = ?
We know that, Focal length f =\(\frac{\mathrm{R}}{2}\)
∴ R = 2f = 2 x 12 = 24cm
Thus, the radius of curvature of the mirror is 24 cm.

Question 17.
What do you mean by focal length of a spherical mirror is 20 cm?
Answer:
1. Focal length (f) is the point at which all the parallel rays meet after getting reflected from the spherical mirror.
2. If the focal length of a spherical mirror is 20 cm it means all the parallel rays that hit the spherical mirror will meet at 20 cm away from the spherical mirror.

Question 18.
At how many positions can we place an object to obtain Images from a concave mirror?
Answer:

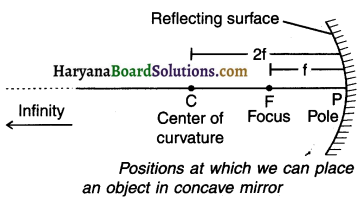
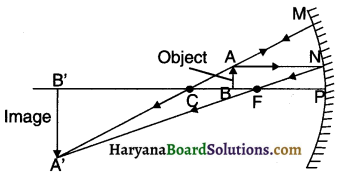
As shown in figure, we can place the objects at six positions. They are:
1. Much beyond C i.e. at infinity
2. Beyond C
3. On center of curvature (C)
4. Anywhere between focus (F) and center of curvature (C)
5. On focus (F)
6. Anywhere between the pole (P) and focus (F)

Question 19.
Draw the ray diagram for a concave mirror when an object s placed at following points. Also give the position, nature and size of image.
Answer:
Object is placed at the following positions:
(1) At infinity
(2) Beyond C
(3) At C
(4) Between C and F
(5) At F
(6) Between P and F
(Note: Each diagram along with its detail carry 2 marks and hence the questions will be asked accordingly. However, here we have given detail of all the positions.)

Images formed by a Concave mirror

Summary of images formed in a concave mirror

Position of object	Position of image	Size of image	Nature of image
1. At infinity	At F	Highly diminished	Real and inverted
2. Beyond C (i.e. 2F)	Between F and C	Diminished	Real and inverted
3. On C (i.e. on 2F)	On C	Same as object size	Real and inverted
4. Between F and C	Beyond C	Enlarged	Real and inverted
5. On principal focus F	At infinity	Highly enlarged	Real and inverted
6. Between P and F	Behind the mirror	Enlarged	Virtual and erect

Question 20.
State the uses of concave mirrors.
Answer:
Uses of concave mirrors:

• Concave mirrors are used in torches, search-lights and vehicle head-lights to obtain powerful parallel beam of lights.
• They are also used in shaving mirrors to see a larger image of the face.
• Dentists use concave mirrors to see enlarged view of teeth an patients.
• To concentrate sunlight for producing heat in solar furnace.

Question 21.
Why are focal length and centre of curvature negative for convex mirrors?
Answer:
1. In a convex mirror, the rays parallel to principle axis, instead of converging at a point in the front of the mirror, appear to diverge from a point behind the mirror. This point is called the focal point or focus F of the mirror. Similarly, the centre of curvature also lies behind the mirror.

2. As per the rule, positions in the front of any mirror will have positive sign and those behind the mirror will have negative signs. Since, F and C both lie behind the convex mirror, their signs are negative.
(Note: (1) The focus of convex mirror is also called virtual focus. (2) f = R/2 holds true for convex mirrors also.)

Question 22.
At how many positions can we place an object to obtain images from a convex mirror? Also explain why we place the object at fewer positions in convex mirror than concave mirror.
Answer:
To obtain an image on a convex mirror we can place our object only at two positions. They are:
(1) At infinity
(2) Between pole P and infinity

Reason:
1. In concave mirrors, the focus F and center of curvature C lie before the mirror. The object is also placed before the mirror and so it can be placed at six positions in concave mirror.

2. In a convex mirror, the focus F and center of curvature C lie behind the mirror. Now, the image is formed only when an object is placed before the mirror and not behind it. Hence, in convex mirror, there can be only two positions for placing the object before the mirror.

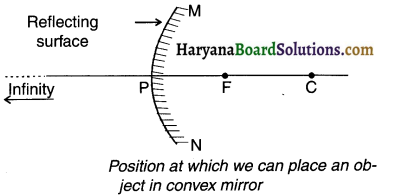
Question 23.
Draw and explain the type of Images formed by convex mirror.
Answer:
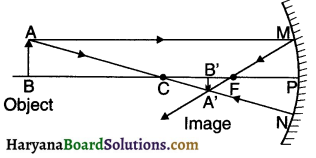
Images formed by a convex mirror

Summary of images formed in a convex mirror

Position of object	Position of image	Size of image	Nature of image
1. At infinity	At focus F, behind the mirror	Highly diminished	Virtual and erect
2. Anywhere between infinity and pole P of the mirror	Between pole P and focus F, behind the mirror	Diminished	Virtual and erect

Question 24.
List out the properties of the image formed by a convex mirror.
Answer:
Properties of image formed by a convex mirror:
(1) The image formed is always virtual and erect.
(2) The image is highly diminished i.e. point sized.
(3) Image is always formed between F and R
(4) As you move the object closer to the pole, the image also moves closer to the pole. It grows in size and at one point becomes equal to the object size.

Question 25.
Explain New Cartesian Sign Convention for reflection by spherical mirror.
Answer:
1. For studying the reflection from spherical mirrors, the method or sign convention called the New Cartesian Sign Convention is used.
2. Here, pole P of the mirror is taken as origin and The principal axis XX’ is taken along the X-axis of the New Cartesian co-ordinate system. The axis drawn perpendicular to principal axis at pole P is considered as Y-axis. According to the New Cartesian Sign

Convention:
(i) The object AB always lies on the left side of mirror and hence light is incident from left side of the mirror.
(ii) All the distances parallel to the principal axis are measured from the pole of the mirror P.
(iii) Distances measured in the same direction as that of incident light (left to right) along the +ve x-axis are taken as positive. x-axis are taken as positive.
→ Distances measured against the direction of incident light (right to left) along the -ve x-axis are taken as negative.
(iv) Distances measured perpendicular to and above the principal axis (along +ve y-axis) are taken as positive.
→ Distances measured perpendicular to and below the principal axis (along -ve y-axis) are taken as positive.

Summary of signs of various distances for concave and convex mirrors.

Note: Refer the New Cartesian Sign Convention while reading the table.

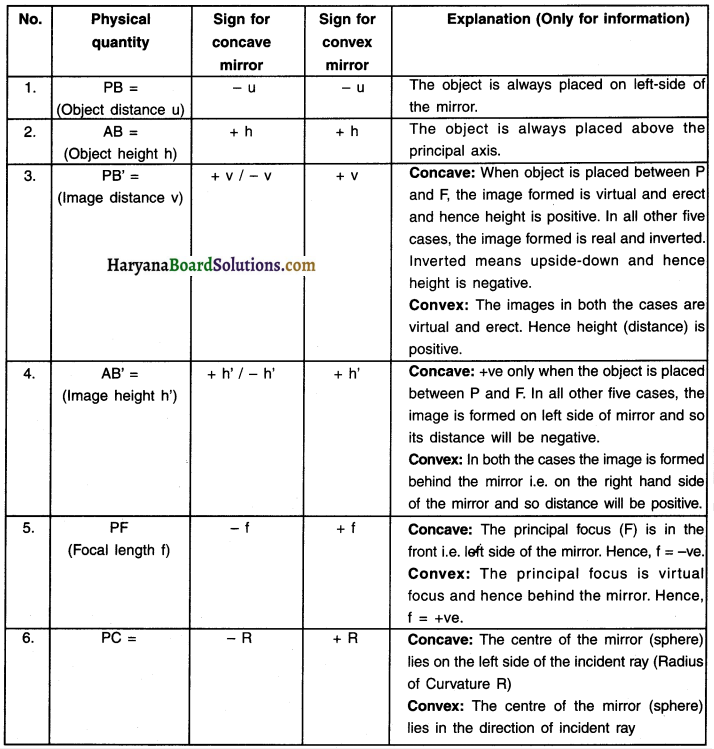
Question 26.
State the mirror formula for concave and convex mirrors.
Answer:
The relationship between the object distance (u), image distance (v) and focal length (f) of a mirror is called the mirror formula.
As per mirror formula:\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
In words: \(\frac{1}{\text { Object distance }}+\frac{1}{\text { Imagedis tance }}=\frac{1}{\text { Focal length }}\)
Object distance image distance Focal length
Mirror formula is same for concave as well as convex mirror.

Question 27.
What do you mean by magnification? State Its definition and give to formula.
Answer:
Magnification:
Whenever we observe the image of an object after reflection by a spherical mirror, there can be a change in the size of the object. This means that the image formed can be larger than the object size, smaller or even of the same size as the object. This phenomenon of change in the image size is known as magnification (m).

Definition:
1. The ratio of image height (h’) to object height (h) is called the magnification (m).
2. Thus, for spherical mirrors, magnification (m) \((m)=\frac{\text { Height of image }\left(h^{\prime}\right)}{\text { Height of object }(h)} \text { i.e. } m=\frac{h^{\prime}}{h}\)
3. In terms of object distance (u) and image distance (y), magnification (m) can be expressed as,
\(m=\frac{h^{\prime}}{h}=-\frac{v}{u}\)
4. If value of m = positive, image is virtual.
5. If value of m = negative, image is real.

The two important aspects of magnification that determines the sign and value of m.
We know magnification\((m)=\frac{\text { Image height }\left(h^{\prime}\right)}{\text { Object height }(h)}\)

There are two important aspects of magnification. They are:
(a) Sign of m, (b) Value of m

(a) Sign of m:

• The sign of m i.e. magnification can be either positive or negtive.
• The sign of m depends on the signs of h’ and h.

(i) Sign of h:  h represents the height of the object. Since the object is always placed above the principal axis, value of h will always be positive.

(ii) Sign of h’:

• represents the height of image.
• If the image is virtual, it will always be erect and hence above the principal axis. Hence, h’ will be positive.
• If the image is real, It will always be inverted and hence below the principal axis. Here, h’ will be negative.

Conclusion:

• m will be positive for virtual images (Since both h and h’ will be positive.)
• m will be negative for real images. (Since h will be positive but h’ will be negative.)
• Concave mirrors can produce both virtual and real images. So, magnification m of a concave mirror can either be positive or negative and vice-versa.
• Convex mirrors and plane mirrors can produce only virtual images. So, their magnification will always be positive and vice-versa.

(b) Value of m:

• The magnification i.e. the value of m can either be greater than 1, equal to 1 or less than 1.
  (i) m> 1
•  If value of m> 1, it means that the size of image > size of object.

Example:
h’ = 10 cm and h = 5 cm
\(m=\frac{h^{\prime}}{h}=\frac{10}{5}=2\)
∴ image size > object size.

(ii) m = 1
If value of m = 1, it means size of image = size of object.

Example:
h’ = 10 cm and h= 10 cm
\(M=\frac{h^{\prime}}{h}=\frac{10}{10}=1\)∴ image size = object size

(iii) m < 1
→  If value of m < 1, it means size of image < size of object.

Example:
h’ = 5, h = 10
\(\mathrm{m}=\frac{\mathrm{h}^{\prime}}{\mathrm{h}}=\frac{5}{10}=\frac{1}{2}=0.5\)
∴ image size <object size

Conclusion:

• Image produced by a plane mirror is always same size as that of object. Thus, m = 1.
•  Image produced by a convex mirror is always diminished i.e. smaller than the object. Thus, m < 1.
• Image produced by concave mirror can be both larger or smaller than the object. Thus, m> 1 or m < 1.

Question 28.
Obtain the position, nature and size of an image formed by a plane mirror from the formula of magnification.
Answer:
1. We know that magnification m =\(\frac{\mathrm{h}^{\prime}}{\mathrm{h}}\)
2. Now in a plane mirror, image height (h’) = object height (h).
3. So we get value of m=+1.
4. The image formed in its case by the plane mirror will be virtual, erect and of same size as the object.
5. Also, magnification m = \(\frac{\mathrm{v}}{\mathrm{u}}\).
6. But, m = 1 and so 1 = \(\frac{\mathrm{v}}{\mathrm{u}}\)
∴ u = -v i.e. y = – u.
7. Since y = – u, the size of the image y will be same as that of the object u but negative sign indicates that the image will be behind the mirror.

Summary of size of image, type of image and magnification for various mirrors

Question 29.
Textbook illustration 10.1: A convex mirror used for rear-view on an automobile has a radius of curvature of 3.00 m. If a bus is located at 5.00 m from this mirror, find the position, nature and size of the Image.
Solution:
Radius of curvature, R = + 3.00 m;
Object-distance, u = – 5.00 m;
Image-distance, v=?
Height of the image, h’ = ?
Focal length, f = R/2 = +\(\frac{3.00 \mathrm{~m}}{2}\) = +1.50m (Since the principal focus of a convex mirror is behind the mirror)

The image is virtual, erect and smaller in size by a factor of 0.23.

Question 30.
Textbook illustration 10.2: An object, 4.0 cm in size, is placed at 25.0 cm in front of a concave mirror of focal length 15.0 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Find the nature and the size of the image.
Answer:
Object-size, h= +4.0cm;
Object-distance, u = – 25.0 cm;
Focal length, f = -15.0 cm;
Image-distance, v = ?
Image-size, h’ = ?

or \(\frac{1}{v}=\frac{-5.0+3.0}{75.0}=\frac{-2.0}{75.0}=\text { or, } v=-37.5 \mathrm{~cm}\)
The screen should be placed at 37.5 cm in front of the mirror. The image is real.
Also, magnification, \(m=\frac{h^{\prime}}{h}=-\frac{v}{u}\)
\(\text { Or, } h^{\prime}=-\frac{v h}{u}=-\frac{(-37.5 \mathrm{~cm})(-4.0 \mathrm{~cm})}{(-25.0 \mathrm{~cm})}\)
Height of the image, h’ = – 6.0 cm. The image is inverted and enlarged.

Question 31.
Differentiate between regular reflection and irregular reflection.
Answer:

Regular reflection	Irregular reflection
When a parallel beam of light is incident on a shining plane or a smooth surface, the light rays remain parallel after reflection in a specific direction. Such reflection is called regular reflection.	When a parallel beam of light is incident on a rough or irregular surface, the incident rays do not remain parallel but spreads over wide region after reflection. Such a reflection of light is called irregular reflection.
Reflected rays are parallel to incident rays.	Reflected rays are not parallel to incident rays.
Example: Reflection of light by a plane mirror	Example: Reflection from chair, book, etc.

Question 32.
Differentiate between concave mirror and convex mirror.
Answer:

Concave mirror
A spherical mirror having inner curved reflecting surface is known as concave mirror.	A spherical mirror having outer curved reflecting surface is known as convex mirror.
Image formed by concave mirror can be real and inverted or virtual and erect.	Image formed by convex mirror is always virtual and erect.
Real image can be smaller size or even larger than the object.	Virtual image will always be smaller than the object.

Question 33.
Differentiate between real image and virtual image.
Answer:

Real image	Virtual Image
An image formed by reflection or refraction of light from the object is called a real image	An image which is not actually formed by reflection or refraction of light from the object is called a virtual image.
It can be obtained on a screen.	It cannot be obtained on a screen.
Real image is in inverted form.	Virtual image is always erect.

Question 34.
Give a brief Introduction about refraction.
Answer:
Refraction:
1. Light travels on a same path i.e. without bending if it is travelling in same transparent medium such as air or water.
2. While travelling if light comes across another transparent medium, its velocity changes and so it bends.
3. For example, if light is travelling in air (medium 1) and then it strikes water (medium 2) obliquely, it bends. This bending of light is called refraction of light.

Question 35.
Define refraction of light. State its laws.
Answer:
Refraction:
When a ray of light enters obliquely from one transparent medium to another transparent medium, its velocity changes due to which it gets deviated from its original direction at the surface separating two medias. This is called refraction.

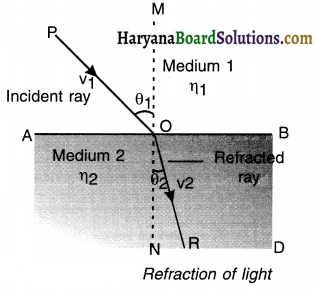
Laws of refraction:
1. Incident ray, refracted ray and normal to the surface separating two medias at the point of incidence, all lie in the same plane.
2. The ratio of the sine of angle of incidence to the sine of angle of refraction is constant for the light of a given colour (wave length) and for the given pair of media. This law is known as Snell’s Law of Refraction.
\(\frac{\sin \theta_1}{\sin \theta_2}=\text { constant }\)
Here, θ₁ = angle of incidence and θ₂= angle of refraction.
Example:
Refraction takes place when light travels from air (medium 1) into glass (medium 2).

Question 36.
With respect to travel of light and its refraction, explain medium and comparative types of mediums. Also explain behaviour of light in these mediums.
Answer:
Medium:

• A transparent substance in which light can travel is called a medium.
• Air, water gas, glass, kerosene, etc. are examples of mecums.
• The densities of each medium are different and so they are classified as follows —

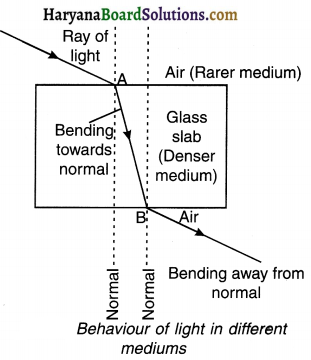
(i) Optically rarer medium:
A medium in which the speed of light is more is called optically rarer medium.

Example:
Air is optically rarer than water and glass.

(ii) Optically denser medium:
A medium in which the speed of light is less (compared to an optically rarer medium) is called an optically denser medium.

Example:
1. Glass is optically denser than air. Kerosene is optically denser than water. Refraction of light in various mediums:
2. When light travels from a rarer medium (e.g. air) to a denser medium (e.g. glass), It bends towards normal at the point of incidence.
3. When light travels from an optically denser medium (e.g. glass) to a rarer medium (e.g. air), it bends away from normal at the point of incidence.

Question 37.
What do you mean by refractive index of a medium?
Answer:
1. A ray that travels obliquely from one transparent medium into another will change its direction in the second medium. This means that the light has refracted.
2. The extent of the change in direction that occurs within the given pair of media (let us say air and glass) can be expressed in the terms of refractive index.

Question 38.
Explain relative refractive index.
Answer:
Relative Refractive Index :
1. The ratio of speed of light v₁ in medium 1 to the speed of light v₂ in medium 2 is known as the relative refractive index of medium 2 with respect to medium 1 (except the medium of vacuum).
2.  It is denoted by η₁₂ i.e. refractive index of medium 2 with respect to medium 1.
∴ Refractive index η₁₂ = \(\eta_{21}=\frac{\text { Speed of light in medium } 1}{\text { Speed of light in medium } 2}=\frac{v_1}{v_2}\)
3. Similarly, the ratio of speed of light 2 in medium 2 to the speed of light y1 in medium 1 is known as the relative refractive index of medium 1 with respect to medium 2.
∴ Refractive index \(\eta_{12}=\frac{\text { Speed of light in medium } 2}{\text { Speed of light in medium } 1}=\frac{v_2}{v_1}\)

Question 39.
Define and explain absolute refractive index.
Answer:
Absolute refractive index:
1. The ratio of speed of light in vacuum (or air) (C) to the speed of light of any other medium is known as the absolute refractive index or simply refractive index.
2. It is denoted by η_m
∴ Absolute refractive index \(\eta_m=\frac{\text { Speed of light in vacuum (or air) }}{\text { Speed of light in medium }}=\frac{\mathrm{c}}{\mathrm{v}}\)

Question 40.
Give Snells law.
Answer:
Snells law:
1. The ratio of sine of angle of incidence to the ratio of sine of angle of refraction is constant.
2. This constant is known as relative refractive index of medium 2 with respect to medium 1 and is denoted by η₂₁.
∴ \(\eta_{21}=\frac{\sin \theta_1}{\sin \theta_2}\)
3. In terms of ratio of velocity of light In two media, the refractive index of light is represented as under –
The ratio of velocity of light v₁ in medium 1 to the velocity of light v₂ in medium 2 is called relative refractive index of medium 2 with respect to medium 1.
∴ \(\eta_{21}=\frac{v_1}{v_2}\)
4. The refractive index of the transparent medium with respect to vacuum is called the absolute refractive index of a medium. It is commonly known as refractive index.

Question 41.
Why do we take absolute refractive index of air = 1?
Answer:
1. Actually the velocity of light in vacuum is slightly more than the velocity of light in air.
2. But for calculating purpose, magnitude of velocity of light in vacuum is taken as equal to the velocity of light in air =
3 x 10⁸m/s
Absolute refractive index of air = \(\frac{\text { velocity of light in vaccum }}{\text { velocity of light in air }}=\frac{3 \times 10^8}{3 \times 10^8}=1\) gives us the value of absolute refraction index of air = 1.
4. Thus, absolute refractive index of air is taken as 1.

Question 42.
Why absolute refractive index Is always greater than 1? Explain with the help of an example.
Answer:
1. Velocity of light is highest in a vacuum.
2. Hence, velocity of light in any other medium will always be lesser than the velocity of light in vacuum or air.
3. In practice, we take the velocity of light in vacuum = velocity of light in air = 3 x 10⁸ rn/s
4. Thus, absolute refractive index
\(\eta=\frac{\text { velocity of light in vacuum }}{\text { velocity of light in medium } 2 \text { i.e. air }}=\frac{3 \times 10^8}{3 \times 10^8}=1\)
5. Now, when we consider absolute refractive index of vacuum or air with any other medium, the answer will always be greater than 1.

Example:
Velocity of light in vacuum (air) = 3 x 10⁸ m/s
Velocity of light in water = 2.25 x 10⁸ m/s
∴ Absolute refractive index of water = \(\frac{\text { velocity of light in vacuum }}{\text { velocity of light in water }}=\frac{3 \times 10^8}{2.25 \times 10^8}=1.33\)
Thus, absolute refractive index will always be greater than 1.

Question 43.
(Activity 10.10) Perform an activity to demonstrate refraction of light through a glass slab.
Answer:
1. Fix a sheet of white paper on a drawing board using drawing pins.
2. Place a rectangular glass slab over the sheet In the middle.
3. Draw the outline of the slab with a pencil. Let us name the outline as ABCD.
4. Take four identical pins.
5. Fix two pins, say E and F, vertically such that the line joining the pins is inclined to the edge AB.
6. Look for the images of the pins E and F through the opposite edge. Fix two other pins, say G and H, such that these pins and the images of E and F lie on a straight line.
7. Remove the pins and the slab.

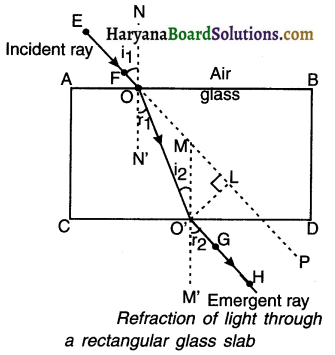
8. Join the positions of tip of the pins E and F and produce the line up to AB. Let EF meet AB at O. Similarly, join the positions of tip of the pins G and H and produce it up to the edge CD. Let HG meet CD at O’.
9. Join O and O’. Also produce EF up to P, as shown by a dotted line in figure.

Observation:
1. At O, light ray along EF enters from air into glass. It bends towards the normal NN’. This is the first refraction.
2. At O’, the light ray enters from glass into air. It bends away from the normal MM’ and travels along GH. This is second refraction.
3. Here, angle of emergence r₂ is equal to angle of incidence t₁, i.e., the emergent ray is parallel to the original direction of the incident ray. This is because there is an identical medium, air in this case, adjacent to both edges AB and CD.
4. However, the light ray is shifted sideways slightly. This is lateral displacement and is represented by O’L.

Conclusion:

• The ray of light travelling from a rarer medium (air) to a denser medium (glass) bends towards the normal.
• The ray of light travelling from a denser medium (glass) to a rarer medium (air) bends away from the normal.
• The emergent ray is parallel to the incident ray but is slightly displaced sideways.

Types: (A) Convex lens:
A lens which is thick at the center and tapered at the upper and lower ends is called a convex lens.

(B) Concave lens:
A lens which is thin in the middle but thicker at the edges is called concave lens.

Uses of lens:
In magnifying glass, cameras, repairing watches, microscope, telescope, etc.

Question 45.
What do you mean by converging and diverging lens?
Answer:
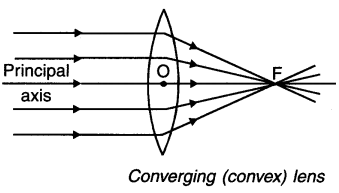
Converging lens:
1. A lens that converges (brings closer) the rays of light travelling parallel to Its principal axis to a point called focus (F) is called a converging lens.
2. Convex lens is a converging lens.

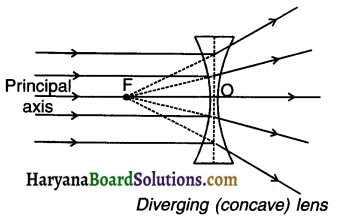
Diverging lens:
A lens that diverges (spreads out) the rays of light travelling parallel to its principal axis is called a diverging lens. If we plot these rays backwards, they appear to diverge from the focus (F) of the lens.
(Note: Lenses have two faces. So light can pass from both sides i.e. left and right.)

Question 46.
Define various terms related to lenses along with suitable diagrams.
Answer:
1. As shown in the diagram, a convex lens (or a concave lens) can be thought of as formed from two spheres.
2. Since there are two spheres and the light can pass from both the sides of a lens, there are two radii, two focuses and two centers of curvature.

1. Centres of curvature:

• The centres of respective spheres of which the surface of lens form parts are called centres of curvature.
• Lens has two centres of curvature denoted by C₁ and C₂.

2. Radii of curvature:

• The radii of spheres of which surfaces of lens form parts are called radii of curvature
• Lens has two radii of curvature denoted by R₁ and R₂.

3. Principal axis: A straight imaginary line passing through the centres of curvature C₁ and C₂ of lens is called the principal axis of lens.

4. Optical centre: The centre of lens, located on principal axis, is known as the optical centre. It is denoted by O.

5. Principal focus: When rays parallel to the principal axis of convex lens are refracted, they converge at a point on the principal axis. This point is called principal focus of the convex lens. A convex lens has two principal foci F₁ and F₂ on either side of lens.

→ The rays parallel to the principal axis of concave lens are refracted such that they appear to be diverging from a point on principal axis. Such a point is called focus of concave lens. Concave lens also has two focii F₁ and F₂ on either side of lens.

6. Focal length
→ The distance between the optical centre (O) and the principal focus (F) is called the focal length of the lens (f).
→ We also mark another point called 2F on the principal axis. This point lies at twice the distance of F.
(Note: In a lens, 2F and C may or may not be at same position.)

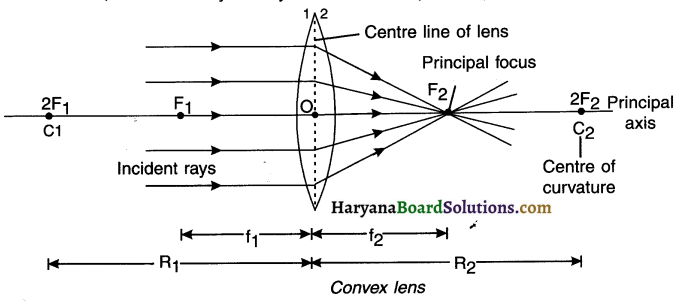
Question 47.
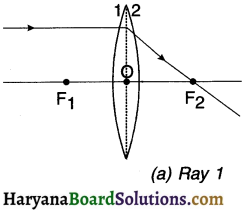
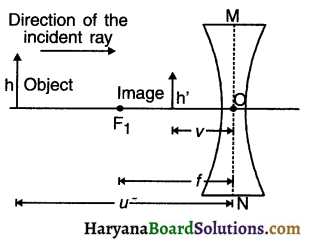
Explain with the help of ray diagram how an image can be formed with convex lens. For obtaining an image through convex lens, we consider the following rays:

Ray 1: It moves parallel to the principal axis and after refraction passes through the principal focus (F₂) on the other side of the lens.

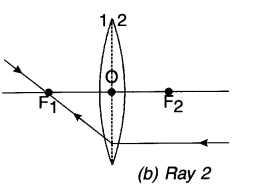
Ray 2: It passes through the principal focus (F₁) and after refraction becomes parallel to the principal axis on the other side of the F lens. 1A

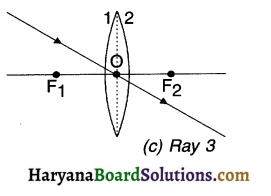
Ray 3: The ray passing through optical centre O will emerge from other side of the lens without any deviation.

Question 48.
List out the various positions at which we can place an object in front of convex lens.

Positions at which we can place an object in front of a convex lens.

(Note: 1. Normally, for both concave and convex lens, the rays are shown coming from the left side of the lens. After refraction they move towards the right side of the lens. 2. The focus F₁ lies on the left side i.e. towards surface 1 of the lens and focus F₂ on the right side i.e., towards surface 2 of the lens.

In a convex lens, an object can be placed at the following positions to obtain its image.
(1) At Infinite distance
(2) Beyond 2F₁
(3) At 2F₁
(4) Anywhere between F₁and 2F₁
(5) At principal focus (F₁)
(6) Anywhere between principal focus (F₁) and optical center (O)

Question 49.
Draw the diagrams for a convex lens when an object is placed at the following points. Also give the position, nature and size of the image.
(1) At infinity
(2) Beyond 2F₁
(3) At 2F₁
(4) Between F₁ and 2F₁
(5) At focus F₁
(6) Between focus F₁ and optical center (O).

(Please note : Each diagram along with its detail carry 2 marks and hence the questions will be asked accordingly. However, we have given detail of all the positions.)

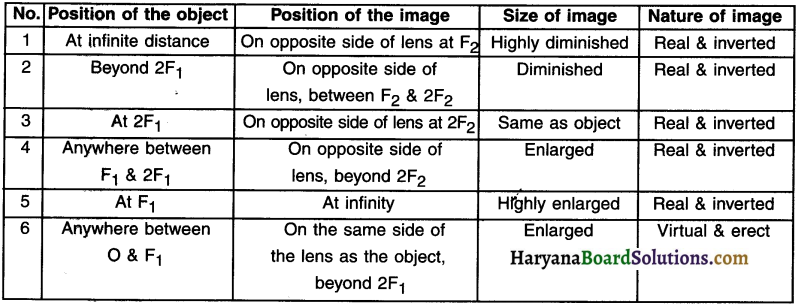
Images formed by a convex lens

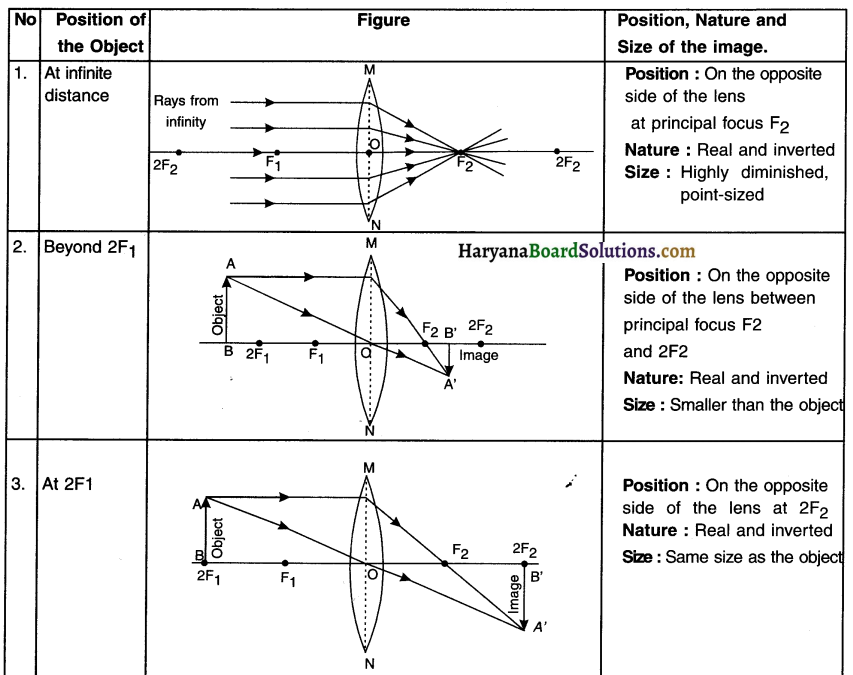
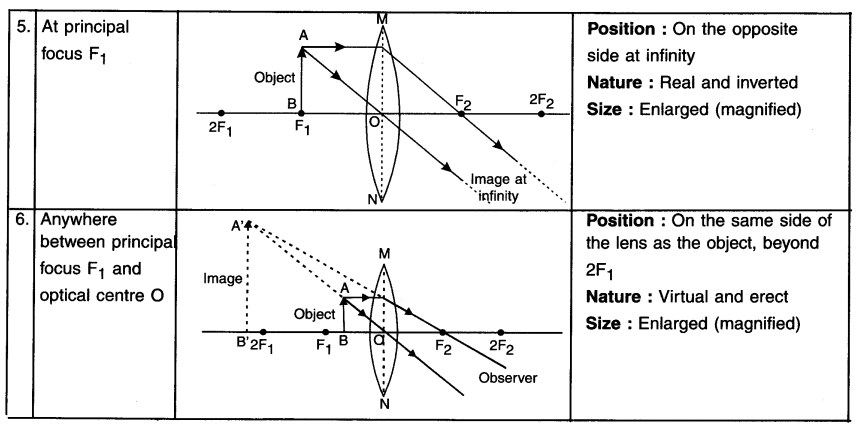
Summary of images formed by convex lens

Question 50.
Draw ray diagram for a concave lens when an object Is placed at (1) Infinity and when object is placed (2) Between infinity and optical centre (O) of the lens.

Images formed by a concave lens

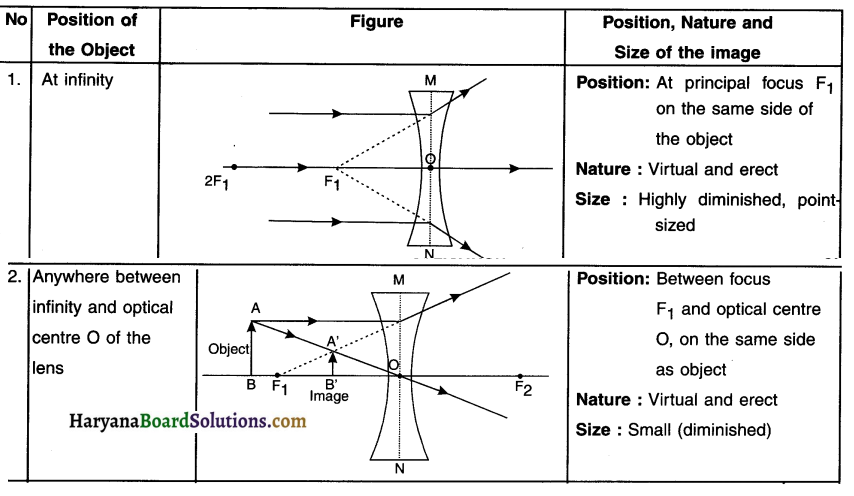
Question 52.
State the New Cartesian Sign convention to be followed for refraction of light through spherical lenses.
Answer:
New Cartesian Sign convention for refraction of light through spherical lenses:
(i) The object is always placed on the left side of the lens. This means that the light is incident on the lens from left side.
(ii) All distances parallel to the principal axis are measured from the optical centre (O) of the lens.
(iii) The distance measured in the same direction as the incident light is taken positive.
(iv) The distance measured in the direction opposite to the direction of incident light is taken negative.

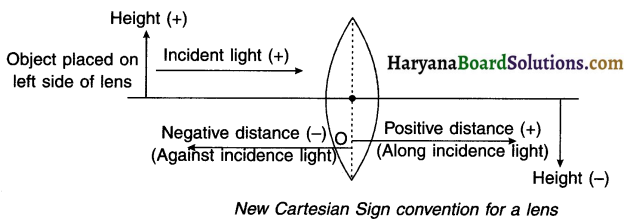
(v) Height measured above the principal axis of the lens and perpendicular to it i.e. in the upward direction is taken as positive.
(vi) Height measured below the principal axis of the lens and perpendicular to it in the downward direction is taken as negative.

New Cartesian Sign Convention followed for refraction of light through spherical lenses
Sign convention for a convex lens:

Object distance = – u
Object height = + h
Image distance = + v for real image
Image height = – h’ for real image
Focal length = + f
Note: If the image is virtual, then image distance
= -v and image height = + h’

Sign convention for a concave lens:

Object distance = – u
Object height = – v
Image distance = – v
Image height = + h’
Focal length = – f

Note: If the image is virtual, then image distance
= – v and image height = + h’
→ Finally, the linear magnification, m = h’/h is positive for a virtual image and negative for a real image

Question 53.
State and explain the lens formula.
Answer:
Lens formula:
(i) The lens formula is a mathematical relation between the object distance (u), image distance (v) and focal length (f) of a spherical lens.
As per lens formula,\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
In other words,\(\frac{1}{\text { Image distance }}-\frac{1}{\text { Objectdistance }}=\frac{1}{\text { Focallength }}\)
Image distance Object distance Focal length
(ii) Lens formula is applicable to both concave lens as well as convex lens.

Question 54.
State the equation for magnification produced by a lens.
Answer:
1. The magnification produced by a lens is defined as “The ratio of the height of the image formed by the lens to the height of the object”.
Thus, magnification m = Height of the image = h’
, Height of the object h \(m=\frac{\text { Height of the image }}{\text { Height of the object }}=\frac{h^{\prime}}{h}\)
Also, \(m=\frac{h^{\prime}}{h}=\frac{v}{u}\)
2. ‘m’ is positive for virtual image formed by the lens.
3. ‘m’ is negative for real image formed by the lens.

Question 55.
Textbook Illustration 10.3: A concave lens has focal length of 15 cm. At what distance should the object from the lens be placed so that it forms an image at 10 cm from the lens? Also, find the magnification produced by the lens.
Solution:
A concave lens always forms a virtual, erect image on the same side of the object.
Image-distance v = -10 cm;
Focal length f = -15 cm;
Object-distance u = ?

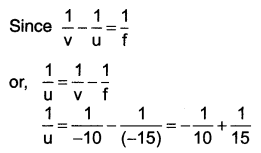
\(\frac{1}{u}=\frac{-2+2}{30}=\frac{1}{-30}\)
Thus, the object – distance is 30 cm.
Magnification m = v/u
\(\mathrm{m}=\frac{-10 \mathrm{~cm}}{-30 \mathrm{~cm}}=\frac{1}{3}=+0.33\)
The positive sign shows that the image is erect and virtual. The image is one-third of the size of the object.

Question 56.
Textbook illustration 10.4: A 2.0 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 10 cm. The distance of the object from the lens Is 15 cm. Find the nature, position and size of the image. Also find its magnification.
Answer:
Height of the object h =+ 2.0 cm;
Focal length f =+ 10 cm;
object-distance u = – 15 cm;
Image-distance v = ?
Height of the image h’ = ?
The positive sign of v shows that the image is formed at a distance of 30 cm on the other side of the optical centre. The image is real and inverted.
Magnification \(m=\frac{h^{\prime}}{h}=\frac{v}{u}\)
or, h’ = h (v/u)
Height of the image, h’ = (2.0) (+30/-15)
= – 4.0 cm
Magnification m = v/u
or \(\mathrm{m}=\frac{+30 \mathrm{~cm}}{-15 \mathrm{~cm}}=-2\)
The negative signs of m and h’ show that the image is inverted and real. It is formed below the principal axis. Thus, a real, inverted image, 4 cm tall, is formed at a distance of 30 cm on the other side of the lens. The image is two times enlarged.

Question 57.
Write a short note on : Power of lens. OR Write definition of power of lens. Give Its SI unit. Name the Instrument used to measure the power of lens.
Answer:
1. The ability of a lens to converge or diverge light rays depends on its focal length.
2. The convex lens of short focal length bends the light rays at large angles by focusing them closer to the optical centre.
3. Similarly concave lens of very short focal length causes higher divergence than the one with larger focal length.
4. The efficiency with which a lens converges or diverges the light rays is expressed in terms of its power.
5. Thus, the power of lens (P) is the “Reciprocal of the focal length (I) of lens”.
Power of lens \((\mathrm{P})=\frac{1}{f}\)
6. The SI unit of power of a lens is diopter and it is denoted by D.
7. If fis expressed in meters, then \(1 D=\frac{1}{1}=1 m^{-1}.\)
8. We can measure the power of lens by using diopter meter.
9. As per Cartesian sign system, focus of convex lens lies on right side of the lens and so power of convex lens is positive, while focus of concave lens lies on left side of lens and so power of concave lens is negative.

Question 58.
Give the sign convention for powers of converging and diverging lenses.
Answer:
1. Converging lens has a positive focal length and so its power (P) is positive.
2. Diverging lens has a negative focal length and so its power (P) is negative.

Question 59.
A pencil when dipped in water in a glass tumbler appears to be bent at the interface of air and water. Will the pencil appear to be bent to the same extent, if instead of water we use liquids like, kerosene or turpentine. Support your answer with reason.
Answer:
1. A pencil when dipped in water in a glass tumbler appears to be bent at the interface of air and water. This happens because the light reaching out from the portion of the pencil inside seems as if it is coming from a different direction as compared to the part above water due to refraction of light.

2. The pencil will look bent at different extents when materials such as kerosene or turpentine are used because their refractive indices are different. This produces deviation from incident ray by different extents.

Question 60.
The film or CCD chip must be placed where the image is focused In order to record a sharp image. Give reason.
Answer:
1. Light from very distant objects reaches the camera in the form of parallel beams.
2. This will allow the light to focus right at the focal point of the lens.
3. Anything closer will have rays that will not be parallel but diverging and so they will be focused at a distance further from the lens than the focal point of the lens.
4. Hence, the film or CCD chip must be placed where the image is focused properly in order to record a sharp image.

Question 61.
Convex mirrors are used In car headlights where as concave mirrors are used in street lights. Give reason.
Answer:
1. Concave mirrors have an ability to form a parallel and powerful beam of light focusing on a particular area.
2. On keeping the bulb of the car head light at the focal point of the reflector, a powerful beam of light is produced. This allows better focusing of the lights and hence the visibility of the driver improves.
3. Whereas, convex mirrors have the ability to diverge the rays over a large area. This brightens a larger area compared to concave mirror.
4. Hence, convex mirrors are used in car headlights where as concave mirrors are used in street lights.

Question 62.
You are given three mirrors of equal sizes — concave, convex and plane. How will you identify them without touching their surfaces?
Answer:
Take one mirror at a time and watch your face in it. First keep the face quite close and then slowly and gradually move the face away from the mirror. Do this in each mirror and decide the type of mirror based on the following observations —

• If the image formed is of same size as our face but laterally inverted i.e. left portion looks right and right looks left for all positions, then it is a plane mirror.
• If the image formed is erect and enlarged initially but gets inverted as the face is moved further, the mirror is a concave mirror.
• If the image formed is erect and smaller in size for all the position, the mirror is convex.

Question 63.
The phrase “Objects in mirror are closer than they appear” is written on the side mirrors of the vehicles. Give reason.
Answer:
1. The side mirrors of the vehicles are convex mirrors.
2. The image obtained through convex mirrors is always diminished.
3. As a result the actual object appears smaller.
4. Since smaller-appearing objects seem farther than they actually are, a driver might change a lane assuming an adjacent vehicle is at a safe distance behind, when in fact it may be quite closer.
5. Thus, the phrase Objects in mirror are closer than they appear” serves as a warning/reminder to the driver of this potential problem.

Question 64.
A diamond kept under water sparkles less as compared to when kept in air. Give reason.
Answer:
1. The sparkling of a diamond actually occurs because of repeated total internal reflection.
2. When light enters a diamond, it is difficult for it to leave because of the high index of refraction so it tends to totally internally reflect inside the diamond.
3. The multiple internal reflection of light in the diamond in different directions, allow it to sparkle.
4. Putting a diamond underwater means that the difference in speeds (or index of refraction) is much less which leads to less total internal reflection. This decreases the sparkle of the diamond.

Question 65.
State the type of mirror preferred as
(i) Rear view mirror In vehicles and
(ii) Shaving mirror. Justify your answer giving two reasons in each.
Answer:
(i) A convex mirror is preferred as a rear-view mirror because —

• Convex mirror always forms a virtual, erect and a diminished (point-like) image of an object placed anywhere in front of it. This means the driver can see the image of person even at a very distant position.
• Convex mirror has a wider field of view. So it covers a large rear distance. This helps the driver as he can see more.

(ii) A concave mirror Is preferred for shaving because —

• When such a mirror is held near the face, the person can see enlarged image of his face. This helps to have a cleaner shave.
• An erect image is formed.

Question 66.
A person in a dark room looking through a window can clearly see a person outside in the daylight, whereas the person outside cannot see the person inside. Give reason.
Answer:
1. When light falls on an object, it absorbs some light and reflects some.
2. If you are inside in the dark, a person outside in bright sunlight is sending out (reflecting) lots of light
3. Most of this light would come through the window to you, so you see them clearly.
4. Since it is so bright outside, there is also a good amount of light, which reflects back towards you.
5. In your case, you are standing in dark and so very little light falls on you. As a result, you do not reflect much light. This makes it difficult for the person standing outside to see you clearly.

Question 67.
Sudha finds out that the sharp image of the window pane of her science laboratory is formed at a distance of 15 cm from the lens. She now tries to focus the building visible to her outside the window instead of the window pane without disturbing the lens. In which direction will she move the screen to obtain a sharp Image of the building? What Is the approximate focal length of this lens?
Answer:
Sudha should move the screen towards the lens to for obtaining a sharp Image of the building.

Reason:
1. The window pane was lying beyond focus 2F i.e. center of curvature and convex lens forms its image, on the other side between F and 2F
2. The building that Sudha sees from her window can be considered as a distant object i.e. at infinity. When Sudha tries to focus the building, the lens forms the Image of building at a distance of focal length. The approximate focal length of this lens is 15 cm.

Question 68.
Raj along with his friend Dipti visited Nagina-wadi in Kankaria, Ahmedabad which has got a variety of mirrors. Raj showed her a mirror In which Dipti’s image showed the upper half of the body very fat and lower half of the body very thin. Dipti thought there is a problem with the mirror. She got embarrassed and also angry. Raj laughed and explained not to worry as the mirror is designed that way.
(1) Can you name the two types of mirrors used?
(2) Name the mirror In which the size of Image ¡s small.
(3) What values are displayed by Raj?
Answer:
(1) Concave and convex mirror
(2) Convex mirror
(3) Compassion and empathy towards Dipti in consoling her and making her calm.

Question 69.
Under what condition in an arrangement of two plane mirrors, the incident ray and reflected ray will always be parallel to each other, whatever may be angle of incidence. Show the same with the help of diagram.
Answer:
When we place two plane mirrors at right angle with each other, then the incident ray and reflected ray will always be parallel to each other, whatever the angle of incidence.

Question 70.
Four friends were on a picnic. Ranjit was driving the car. Suddenly he noticed that in his side mirror that the car which was behind their car had met with an accident. He immediately stopped his car and the friends decided to help the injured person. All of them took the Injured person to the nearest hospital. After taking first-aid from the hospital, the victim thanked them for saving his life.
(1) Name the type of mirror from which Ranjit saw the accident.
(2) Why is this type of mirror used as a side mirror in vehicles?
(3) Which values are displayed by Ranjit?
Answer:
(1) A convex mirror
(2) Convex mirrors, have wider field of view, as they are curved outwards. Therefore, a convex mirror enables the driver to view much larger area.
(3) Ranjit displayed alertness as well as duty of a citizen towards other. The friends also displayed selflessness and empathy.

Question 71.
A child is standing in front of a magic mirror. She finds the image of her head bigger, the middle portion of her body of the same size and that of the legs smaller. The following is the order of combinations for the magic mirror from the top. Which combination do you think is correct? Justify your reason.
(1) Plane, convex and concave,
(2) Convex, concave and plane
(c) Concave, plane and convex,
(d) Convex, plane and concave
Answer:
1. Combination (c) Concave, plane and convex is the correct combination.
2. Concave mirrors of large focal length can be used to see a larger image of the head, the plane mirror for middle portion to see the body of the same size whereas convex mirror to see the diminished image of leg.
3. Hence, the selected combination is correct.

Question 72.
A pencil when dipped in water in a glass tumbler appears to be bent at the Interface of air and water. Will the pencil appear to be bent to the same extent, if instead of water we use liquids like, kerosene or turpentine. Support your answer with reason.
Answer:
1. A pencil when dipped in water in a glass tumbler appears to be bent at the interface of air and water. This happens because the light reaching out from the portion of the pencil inside seems as if it is coming from a different direction as compared to the part above water due to refraction of light.
2. The pencil will look bent at different extents when materials such as kerosene or turpentine are used because their refractive indices are different. This produces deviation from incident ray by different extents.

Question 73.
If an object of 4 cm height Is placed at a distance of 18 cm from concave mirror having focal length 12 cm, find the position, nature and height of the image.
Answer:
Object height h = 4 cm
Object distance u = -18 cm
Focal length f = -12 cm
(Both, principal focus F and u lie to the left of concave mirror, hence negative.)
From mirror formula,

Conclusion:
1. Magnification is positive, h’ is negative which indicates image is real and inverted. Also, it is enlarged compared to object.
2. The image is formed 36 cm on the left side of pole P beyond the center of curvature C.

Question 74.
A convex mirror Is fitted on an automobile with focal length of 3 m. If a vehicle behind is at a distance of 5 m, determine the position and nature of an image.
Answer:
Object distance u = – 5 m
Focal length f = 3 m
(f is positive because focus of convex mirror lies on right side of pole P)
From mirror formula,

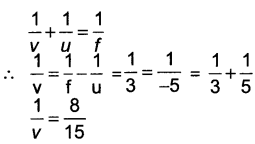
\(v=\frac{15}{8}\) = 1.875m
Here, y is positive and y < u
∴ m<1
Therefore, virtual, erect and diminished image behind the convex mirror is obtained at a distance 1.875 m from the mirror.

Question 75.
An object of height 5 cm is placed at a distance of 10 cm from convex mirror of focal length 15 cm. Find the position, nature and size of an image.
Answer:
Object distance u = -10 cm
Focal length f = 15 cm
Object height h = 5 cm
According to mirror formula,

Here, image distance v is positive and h’ is positive so, we get a virtual image of 3 cm height behind the mirror which is erect and diminished.

Question 76.
Refractive index of media A, B, C and D are

In which of the four media is the speed of light (i) maximum and (ii) minimum? Find the refractive index of medium C with respect to medium B.
Answer:
(i) Speed of light is maximum is medium A for which n (= 1.33) is minimum
(ii) Speed of light is minimum in medium D for which n (= 1.65) is maximum. Refractive index of medium C with respect to medium B.
\(\mathrm{n}_{\mathrm{CB}}=\frac{\mathrm{n}_{\mathrm{C}}}{\mathrm{n}_{\mathrm{B}}}=\frac{1.52}{1.44}=1.05\)

Question 77.
(a) The refractive index of Ruby is 1.71. What is meant by this statement?
(b) The refractive index of some medium are given below:
Crown glass – 1.52, Water – 1.33, Sapphire  – 1.77
In which of the medium is the speed of light:
(i) Maximum (ii) Minimum?
(c) Calculate speed of light in sapphire.
Answer:
(a) The refractive index of ruby is 1.71. It means that the ratio of the speed of light in vacuum to the speed of light in Ruby is 1.71.

(b) (i) Speed of light is maximum in water for which n (= 1.33) is minimum
(ii) Speed of light is minimum in sapphire for which n (= 1.77) is maximum

(c)

Question 78.
Light enters from air to glass having refractive index 1.5. What is the speed of light in glass? The speed of light in vacuum is
3 x 10⁸ m/s.
Answer:
Absolute refractive index of glass
n = \(\frac{\mathrm{c}}{\mathrm{v}}\) and c = 3 x 10⁸ m/s^-1
\(v=\frac{c}{n}=\frac{3 \times 10^8}{1.5} m/s^-1\) (n = 1.5) = 2 x 10⁸ m/s^-1[/latex]

Question 79.
A light ray enters from air to the water medium having the absolute refractive index 1.33. If the angle of refraction of light is 17°30’, what will be the angle of incidence at the surface separating the two media ? Take absolute refractive index of air as 1.00.
Answer:
Taking air as medium 1 and water as medium 2,
n₁ = 1, n₂ = 1.33, θ₂ = 17°30’
According to Sneil’s law,
n1 sin θ1 = n2 sin θ2
sin θ₁ = 1.33 X 17°30’
The value of sin 17°30’ is determined from the Mathematical table of natural sine.
sin 17°30’ = 0.3
∴ sin θ₁ =1.33 x 0.3 = 0.4
∴ From the table of natural sine
sin 23° 36’ = 0.4007
∴ θ₁ = 23° 36’
∴ Angle of incidence = 23° 36’

Question 80
The refractive index of light entering glass from water is 1.12. Find the absolute refractive index of water if the absolute refractive index of glass is 1.5.
Answer:
Here, we take water as medium 1 and glass as medium 2.
Absolute refractive index of glass η₂= 1.5
Absolute refractive index of glass with respect to water η₂₁ = 1.12
Therefore, absolute refractive index of water η₁ =?

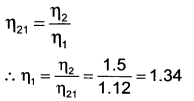
Thus, absolute refractive index of water is = 1.34

Question 81.
A swimmer lights a torch under the surface of sea water. Light from the torch is incident on water surface In such a way that incident light makes an angle 370 with water surface. Find the angle of refraction. Absolute refractive index of water is 1.33 and absolute refractive index of air is 1.0.
Answer:
Taking medium 1 as water, we get η₁ = 1.33
Taking medium 1 as water, we get η₂ = 1.00
Incident angle θ₁ = 37°
Angle of refraction θ₂ = ?
Using the formula, =

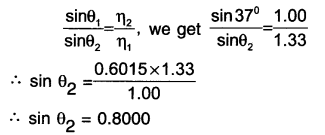
Angle of refraction θ₁ = 53° (from log table).
∴ The value of angle of reflection is equal to 53°

Question 82.
A convex lens forms a real and inverted image of an object at a distance of 40 cm from it. What will be the distance of an object if size of an image is same as the object? Determine the power of lens.
Answer:
Given:
Lens = Convex
Image = Real and inverted
Size of image h’ = object size h
Now, \(m=\frac{h^{\prime}}{h}\)
But, h’= h ∴ m=1.
The image is inverted. ∴ h’ will be negative.
∴ magnification on will be -1.
(Note: You can also think this way. For a convex lens, if the image is real and inverted, the magnification will be negative.)

Thus, object distance = – 40 cm and also image distance = 40 cm.
Substituting, values of y and u in lens formula we get,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)

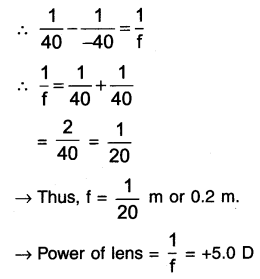
Question 83.
The object of 5 cm height is placed at a distance 25 cm from the centre of convex lens of focal length lo cm. Draw a ray diagram and find position, nature and the size of an image formed.
Answer:
1. Take a scale 2.5 cm = 1 unit on principal axis and draw a ray diagram. The ray diagram is shown below.
2. This shows that real, inverted and diminished image of an object is formed on other side of lens at a distance of 16.67 cm from the lens.
3. Also, h’ = – 3.33 cm

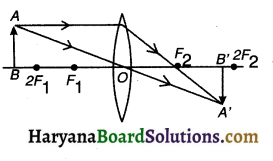
As per lens formula,

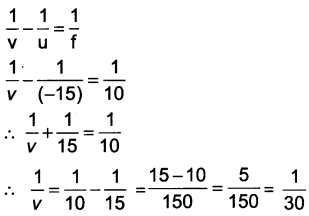
Image will be formed on the other side of the lens at a distance of 30 cm.

Question 84.
An object Is placed perpendicular to the principal axis of concave lens focal length 30 cm. Find the position of an image when the object is at a distance 20 cm from the lens.
Answer:
The focal length of lens f = -30 cm
Object distance u = -20 cm, image distance v = ?
As per the lens formula,

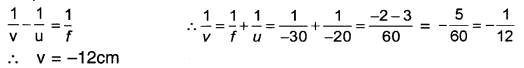
The image will be obtained on the same side of the object at a distance of 12 cm from lens.

Question 85.
The magnification produced by a spherical lens is +2.5. What is the
(a) Nature of image
(b) Nature of lens?
Answer:
(a) When the magnification is positive, then the image is virtual and erect. In this case, the magnification has a positive sign, so the nature of image is virtual and erect.
(b) The value of magnification given here is 2.5 (which is more than 1). So, the image is larger than the object. A virtual, erect and magnified can be formed only by a convex lens, therefore, the nature of lens is convex.

Question 86.
Power of a convex lens is +4.0 D. At what distance should the object from the lens be placed to obtain its real and inverted image of the same size on the screen?
Answer:
1. The focal length of this convex lens is + 4D. As per formula \(p=\frac{1}{f(\text { in meters })}\) we get
\(f=\frac{1}{p}=\frac{1}{4}\) = 0.25m = 25cm
2. Now, in a convex lens, when the image size is same as object size, then the object should be placed from the lens at a distance of 2f.
3. Thus, object distance = 2f = 2 x 25 = 50 cm.

Question 87.
Two thin lenses of power +3.5 D and – 2.5 D are placed in contact. Find the power and focal length of the lens combination.
Answer:
Power of combination of lenses, p = p₁ + p₂
So, p = + 3.5 + (-2.5)
p=+3.5 – 2.5
p = + 1.0 D
Thus, the power of this combination of lenses is, + 1.0 diopter.
We will now calculate the focal length of this combination of lenses. We know that:
Power, \(P=\frac{1}{f} \text { or }+1=\frac{1}{f}\)= and f= +1 m
So the focal length of this combination lens is + 1 meter.

Question 88.
You have two lenses A and B of focal lengths + 10 cm and -10 cm respectively. State the nature and power of each lens. Which of the two lenses will form a virtual and magnified Image of an object placed 8 cm from the lens? Draw a ray diagram to justify your answer.
Answer:
Here, = + 10 cm, = – 10 cm

Lens A is convex and lens B is concave. Lens A will form a virtual and magnified image when the object is placed as 8 cm from it.

Question 89.
If the absolute refractive indices of water, benzene, and sapphire are 1.33, 1.50 and 1.77 respectively, then which medium has maximum relative refractive index?
(i) Sapphire relative to water
(ii) Sapphire relative to benzene
(iii) Benzene relative to water
(iv) Water relative to benzene
Answer:
Absolute refractive index of water = 1.33,
Absolute refractive index of benzene = 1.5, and Absolute refractive index of sapphire r = 1.77,
(A) Relative refractive index of sapphire η₃ to water η₁  i.e. = η₃₁ =\(\frac{\eta_3}{\eta_1}= 1.77/1.33\) = 1.33
(B) Relative refractive index of sapphire η₃ to benzene η₂ i.e. = η₃₂= \(\frac{\eta_3}{\eta_2}\)= 1.77/1.5 = 1.18
(C) Relative refractive index of benzene η₂ to water η₁ i.e. = η₂₁ =\(\frac{\eta_2}{\eta_1}=1.5/1.33\)= 1.12
(D) Relative refractive index of water η₁ to benzene η₂ i.e. η₁₂ =\(\frac{\eta_1}{\eta_2}= 1.33/1.5\)= 0.88
Thus, sapphire to water has the highest relative refractive index.

Question 90.
It he absolute refractive indices of water and glass are 4/3 and 3/2 respectively, then what will be the ratio of velocity of light In water to that of glass?
→ 8/9
Solution:
Absolute refractive index of water = \(\eta_1=\frac{4}{3}\)
Absolute refractive index of glass = \(\eta_2=\frac{3}{2}\)
∴ Ratio of velocity of light in water to glass will be \(\eta_{21}=\frac{v_1}{v_2}\)

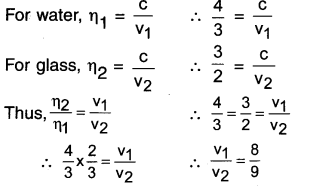
Very Short Answer Type Question

Question 1.
What is reflection? State its types.
Answer:
The phenomenon of sending back the light rays which fall on the surface of an object when light is incident on it, is called reflection of light.
Types:

• Regular reflection and
• Irregular (diffused) reflection.

Question 2.
What is regular reflection?
Answer:
1. When a parallel beam of light falls on a smooth or shining surface, then the reflected beam is also parallel and directed back in a fixed direction.
2. This type of reflection is known as regular reflection. E.g. reflection by a mirror.

Question 3.
What is irregular or diffused reflection?
Answer:
1. When a parallel beam of light falls on a rough surface or irregular surface, then reflected light is not parallel but spreads over a wide area.
2. This type of reflection is known as irregular reflection.

Question 4.
State the laws of reflection.
Answer:
(i) The angle of incidence (θi) is equal to the angle of reflection θr i.e. θi = θr.
(ii) The incident ray, the normal to the mirror at the point of incident and the reflected ray, all lie in the same plane.

Question 5.
Define angle of incidence.
Answer:
The angle that incident ray makes with normal drawn at the point of incidence is known as incident angle or angle of incidence. It is denoted by θ_i.

Question 6.
Define angle of reflection.
Answer:
The angle that reflected ray makes with normal drawn at the point of reflection is known as reflection angle or angle of reflection. It is denoted by θ_r.

Question 7.
What is a plane mirror?
Answer:
A plane mirror is a thin, flat and smooth sheet of glass having a shining coating of silver metal on one side.

Question 8.
What happens when a parallel beam of light is Incident on shining plane or smooth surface?
Answer:
The beam remains parallel after reflection a specific direction

Question 9.
What is a spherical mirror?
Answer:
1. A spherical mirror is a mirror whose reflecting surface is in fact a part of a hollow sphere of a glass.
2. Unlike plane mirrors, a spherical (curved) mirror converges or diverges parallel light rays incident on them.

Question 10.
Draw a labeled diagram showing various parts of a concave mirror.
Answer:

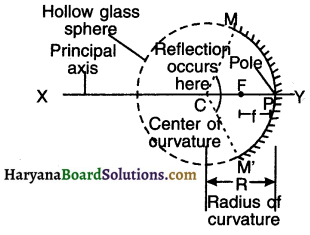
Question 11.
State the relation between radius and focal length of a spherical mirror.
Answer:
Radius of curvature (R) = 2 times focal length (f)
∴ \(f=\frac{R}{2}\)

Question 12.
Radius of a mirror is 25 cm. What will be its focal length?
Answer:
R = 2f \(f=\frac{R}{2}=\frac{25}{2}\) = 12.5 cm.

Question 13.
What should be the position of an object with respect to focus of a convex lens of focal length 20 cm, so that its real and magnified image is obtained? Draw a ray diagram to show the image formation.
Answer:
1. Given that f = 20 cm.
2. To obtain real and magnified image, the object should be placed between F₁ and 2F₂. Hence, the range will be between 20 cm to 40 cm.

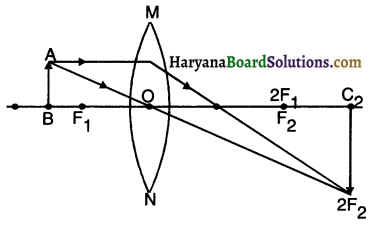
Question 14.
Draw a labeled diagram showing various parts of a convex mirror.
Answer:

Question 15.
How does a ray parallel to the principle axis behaves In a concave mirror? Show with diagram.
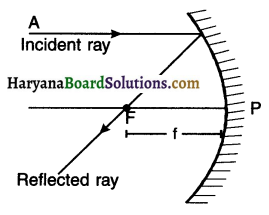
Answer:
Ray parallel to principal axis which after reflection passes through principal focus F.

Question 16.
How does a ray that passes through the principle focus of a concave mirror behaves? Show with diagram.
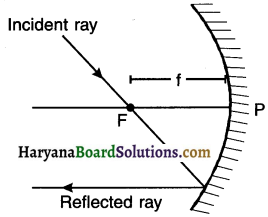
Answer:
Ray passing through the principle focus will become parallel to the principle axis after reflection.

Question 17.
Draw the diagram for a ray directed towards principle focus and its reflection through a convex mirror.
Answer:

Question 18.
Look at the diagram and describe the position, nature and size of the image formed.
Answer:

Position: Beyond centre of curvature C
Nature: Real and inverted
Size: Magnified

Question 19.
For a concave mirror, draw the diagram for image formed when the object is placed beyond C.
Answer:

Question 20.
Fill the table with respect to concave mirror.
Answer:
(1) Position of image — On c, Nature — Real and inverted,
(2) Position of object — Behind the mirror, Nature — Virtual and erect

Question 21.
State one use of convex mirrors.
Answer:
It is used as rear-view mirrors in vehicles.

Question 22.
ROM wants to have an erect Image of an object using a converging mirror of focal length 40 cm.
(i) Specify the range of distance where the object can be placed in front of the mirror. Give reason for your answer.
(ii) Will the image be bigger or smaller than the object?
Answer:
(i) To have an erect image of an object, the position of object should be between pole of the concave mirror and its focus, i.e. between 0 to 40 cm.
(ii) The image formed will be magnified i.e. image will be bigger than the object.

Question 23.
Raghav drew the following diagram in which a ray of light is incident on a convex mirror. You need to redraw the diagram and complete the path of the ray after It gets reflected from the mirror.
Answer:

Question 24.
The focal length of a concave mirror is 20 cm. Where will you place the object if you want an image which is real, inverted and of same size as the object?
Answer:
40cm

Question 25.
A concave mirror produces a real image which is five times magnified as compared to the object. The object is placed at 15 cm in the front of the mirror. At what distance will the image be produced?
Answer:
75cm
(Hint: magnification m = -v/u.
Since image is real, take – m instead of m. Object lies to the left of the mirror and so u = -u
∴ – m = -v/-u)

Question 26.
What is the angle of incidence for a ray of light passing through the centre of curvature of a concave mirror?
Answer:
0°

Question 27.
State the mirror formula.
Answer:
The formula which gives relation between object distance (u), image distance (v) and focal length (f) of a spherkal mirror is known as the mirror formula.
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)

Question 28.
Define magnification of spherical mirror.
Answer:
The ratio of image height (h’) to the object height (h) of the spherical mirror is called the magnification of the mirror.

Question 29.
State the formula of magnification.
Answer:
Magnification \(m=\frac{\text { Image height }\left(h^{\prime}\right)}{\text { Object height }(h)}=-\frac{v}{u}\)

Question 30.
For a mirror, h’ = 10 cm and h = 5 cm. Give its magnification.
Answer:
\(M=\frac{h^{\prime}}{h}=\frac{10}{5}=2\)

Question 31.
If m < 1, state the relation between image size and object size.
Answer:
If m < 1, image size < object size.

Question 32.
What will be the magnification of an object whose height is 4 cm and which produces a real image of 6 cm height?
Answer:
-1.5cm

Question 33.
What is refraction?
Answer:
When a ray of light enters obliquely from one transparent medium to another transparent medium, its velocity changes due to which it gets deviated from its original direction at the surface separating two medias. This is called refraction.

Question 34.
Look at the diagram given here and watch the alphabets. Now write the correct sequence of (a) angle of incidence, (b) angle of emergence, (c) angle of refraction and (d) lateral displacement shown in the diagram as a, b, c and d.

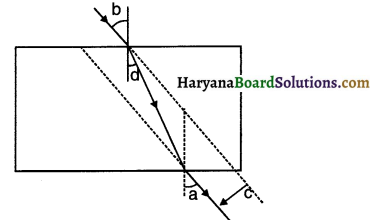
Answer:
The correct sequence is b, a, d, c

Question 35.
What is relative refractive index?
Answer:
1. The ratio of speed of light v₁ in medium 1 to the speed of light v₂ in medium 2 is known as the relative refractive index of medium 2 with respect to medium 1 (except the medium of vacuum).
2. It is denoted by 21 i.e. refractive index of medium 2 with respect to medium 1.

Question 36.
State the two factors that determine lateral displacement of a ray of light passing through a rectangular glass slab.
Answer:
(i) Lateral displacement is directly proportional to the thickness of optical glass slab.
(ii) Lateral displacement is directly proportional to the angle of incidence.

Question 37.
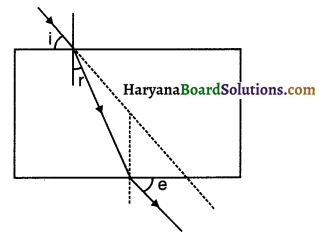
A student traces the path of a ray of light passing through a rectangular glass slab. Which angle is correctly marked?
Answer:
→ r

Question 39.
What is absolute refractive index?
Answer:
1. The ratio of speed of light in vacuum (or air) (c) to the speed of light of any other medium is known as the absolute refractive index or simply refractive index.
2. It is denoted by ‘i’

Question 40.
State the equation for absolute refractive Index.
Answer:
∴ Absolute refractive index η
\(=\frac{\text { speed of light in vacuum }}{\text { speed of light in medium }}=\frac{\mathrm{c}}{\mathrm{v}}\)

Question 41.
What is Snell’s law? Give its equation.
Answer:
1. The ratio of sine of angle of incidence to the ratio of sine of angle of retraction is constant.
2. This constant is known as relative,e refractive index of medium 2 with respect to medium 1 and denoted’ by η₂₁
∴ \(\eta_{21}=\frac{\sin \theta_1}{\sin \theta_2}\)

Question 42.
Observe the following incomplete ray diagram, where the image AB’ is formed after refraction from a convex lens:
On the basis of the above information, fill in the blanks:
(1) The position of object AB (not shown In the figure) must be ………………….
(2) The size of the object must be Than the size of the image.
Answer:

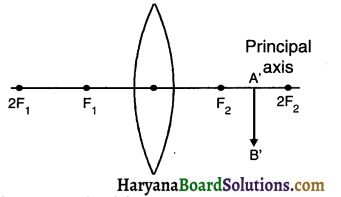
(1) beyond 2F₁ (2) greater.

Question 43.
Akash took a candle and focused the image of its flame on a white screen with the help of a convex lens.
He recorded the following distances —
(1) Position of the candle (object) = 26 cm,
(2) Position of the convex lens = 50 cm, (3)
Position of the screen = 74 cm. Based on the given information calculate the focal length of the convex lens.
Answer:
Here, u = – (50 – 26) = – 24.0 cm
From the lens formula

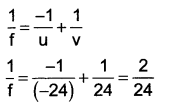
∴ focal length f = 12 cm

Question 44.
What will you call a point inside a lens through which the light passes without deviation?
Answer:
Optical centre

Question 45.
What causes more bending of light rays passing through it – (1) A convex lens of long focal length or (2) A convex lens of short focal length?
Answer:
A convex lens of short focal length

Question 46.
State the equation for power of lens
Answer:
Power (P) = \(\frac{1}{f}\)

Question 47.
The magnification of an image formed by a convex lens is -1. Find the object distance in terms of its focal length.
Answer:

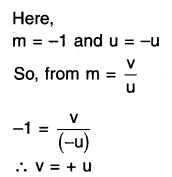
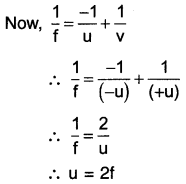
Question 48.
Look at the two ray diagrams given here. In which diagram will magnification be positive? Why?
Answer:
Magnification is positive in diagram (ii).

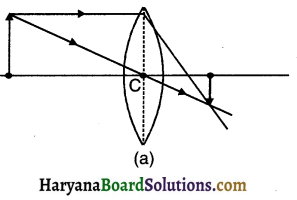
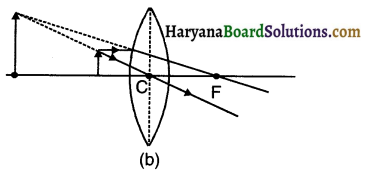
Reason: The image formed is virtual, erect and magnified. This means both the object and the image have positive heights.

Question 49.
Kruti says a thick convex lens has more power as compared to a thin convex lens. Is she correct? State your argument.
Answer:
Yes she is correct because thick convex lens has shorter focal length and hence more power.

Question 50.
What is the SI unit of power of lens?
Answer:
Dioptre
(Hint: Use magnification formula m Image height h’.
\(=\frac{\text { Image height } \mathrm{h}^{\prime}}{\text { object height } \mathrm{h}}\) Real images are negative object height h images.)

Question 51.
A lens has a focal length of -25 cm. What will be the power and nature of this lens?
Answer:
4D; concave

Fill in the Blanks:

1. We cannot see things through regular reflection because …………..
Answer:
The light is reflected back only in one direction.

2. As per the law of reflection, the incident ray, the normal and the reflected ray are …………….
Answer:
In same plane

3. Image formed by plane mirror is ………… (Answer in terms of image property).
Answer:
Virtual and erect.

4. The size of image formed by plane mirror is same as object but is ……………….
Answer:
Laterally inverted

5. Light is ……………..
Answer:
Electromagnetic radiation which produces sensation in our eyes

6. If there is no reflection, the world would appear ……………
Answer:
Dark

7. ……….. and ……….. are the different types of reflection.
Answer:
Regular; Irregular

8. If the …………. surface is made reflecting, one can get a convex mirror.
Answer:
Outer

9. The centre of spherical glass ball is called of ……………… mirror.
Answer:
Centre of curvature

10. The …………… of the reflecting surface of the mirror is known as aperture.
Answer:
Diameter

11. The distance between pole and of mirror is called
Answer:
Focal length

12. …………….. Surfaces which are light in large amount.
Answer:
Completely polished

13. …………… image will be formed actually meet at some point.
Answer:
Real

14. …………….. mirror is used for close shaving.
Answer:
Concave

15. You can see a full length image of a tall building/tree in a ………………. mirror.
Answer:
Convex

16. If you visit Agra Fort you can see the distant full length view of the Taj Mahal in …………………….. mirror fitted there.
Answer:
Convex

17. In a concave mirror, a ray which is parallel to principal axis after reflection will ……………….
Answer:
Pass through the principal focus

18. In a concave mirror, a ray which is passing through centre of curvature will …………….
Answer:
Reflect back along the same path

19. The image formed by a concave mirror is at centre of curvature, real and inverted and same size as object. The position of the objects is …………………
Answer:
At centre of curvature principal focus reflect incident if the light rays

20. For a convex mirror, if the position of the object is at infinity, then the position, nature and size of the image will be ………..
Answer:
At focus, virtual and erect, highly diminished

21. An object of size 1 cm is placed at a distance of 15 cm from a concave mirror of focal length 10 cm. The image distance will be ………………
Answer:
30cm
(Hint: Use mirror formula and follow sign convention.)

22. As per New Cartesian Sign Convention, the object is always placed to the of the mirror.
Answer:
Leftside

23. All the distances parallel to the principle axis are measured from
Answer:
The pole of the mirror.

24. A negative sign in the value of magnification indicates that the image is …………………..
Answer:
Real

25. In mirror formula, as per the sign convention, the image is taken as ……………….
Answer:
-v

26. In mirror formula, as per the sign convention, radius of curvature is taken as ……………….
Answer:
-R

27. Mirror formula can be represented as ………………
Answer:
\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)

28. The ratio of image height to the object height is called …………….
Answer:
Magnification

29. The positive value of magnification represents ……………….. image of an object.
Answer:
Virtual

30. ……… medium retracts most of the light incident on it.
Answer:
Transparent

31. Suppose that the radius of curvature R of a spherical mirror is 30 cm. In this case, its focal length (t) will be …………..
Answer:
15cm

32. The ratio of sine of angle of incidence to the sine of angle of refraction remains constant, subjected lo certain conditions. This law is known as …….
Answer:
Snell’s law of refraction

33. A medium in which speed of light is more is called ……………
Answer:
Optically rarer medium.

34. The sideways Shift of emergent ray from the direction of incident ray is called Lateral shift
Answer:
Leternal shifts

35. According to Snell’s Law constant.
Answer:
\(\frac{\sin \theta_1}{\sin \theta_2}\)

36. When a ray of light travels from optically denser to optically rarer medium,………………
Answer:
It moves away from normal

37. The formula for absolute refractive index is ……………………
Answer:
Velocity of light in vacuum (or air)! Velocity of light in medium

38. The refractive index of water in Which light travels from air is 1.33. Thus, the refractive index of light going from water to air will be ……………….
Answer:
0.75

39. For a convex lens. if an object is positioned at infinity, then the position, nature and size of the image will be and …………….
Answer:
Opposite side at F, real and Inverted, highly diminished (point sized)

40. For a convex lens, ¡f the image is between F and 2F, real and inverted and diminished, then the object should be …………
Answer:
Beyond 2F

41. In a convex lens, If we put an object at 2F, we get its image also on other side of lens at 2F but real and inverted and
Answer:
Of same size

42. In a concave lens, If we wish to have an image between focus F and optical centre O we should place the object…………..
Answer:
Between infinity and optical centre O of the lens

43. ………………………….. the power of lens having 1m kcal length.
Answer:
1D

44. A person having myopic eyes uses a concave lens of local length 75 cm. The power of his lens will be ………………………

True or False

1. The incident ray, normal to the mirror at the point of incidence and the reflected ray, all lie in the same plane. — True
2. A shining spoon can be considered as a plane mirror. — False
3. Focal length (f) = 2R. — False
4. Minimum three rays are needed to construct a ray diagram. — False
5. SpherIcal mIrrors are the most commonly used curved mirrors. True or false. — True
6. Convex mirror is commonly used for shaving. — False
7. You can put an object at only two positions to obtain an image through a convex mirror. — True
8. Concave mirrors are commonly used as rear-view mirrors in vehicles. True or false? — False
9. Concave mirrors have wider field of view. — False
10. For W > h,m > 1 — True
11. Speed of light in a medium / Speed of light in air will give you absolute refractive Index. — True
12. Concave lens is a converging lens. — False
13. Lens formula and mirror formula differ only by a mathematical sign. — True
14. Sideways shifting of the light In a glass slab is called lateral shift. — True

Match the Following 

Question 1.

A	B
1. A perpendicular drawn at the point of incidence to the reflecting surface.	(a) Linear magnification
2. The rays which strike the mirror surface near the periphery	(b) Normal
3. The ratio of the height of the image to the height of the object	(c) Absolute refractive index
4. The ratio of speed of light in vacuum to the speed of light in a medium	(d) Marginal ray

Answer: (1-b), (2-d), (3-a), (4-c)

Question 2.

(A)	(B)
1. Plane mirror	(a) Real image, inverted and large
2. Concave lens	(b) Virtual image, erect and same size
3. Convex lens	(c) Virtual image, positive focal length
4. Convex mirror	(d) Virtual image, negative focal length negative power

Answer: (1-b), (2-d), (3-a), (4-c)

Question 3.

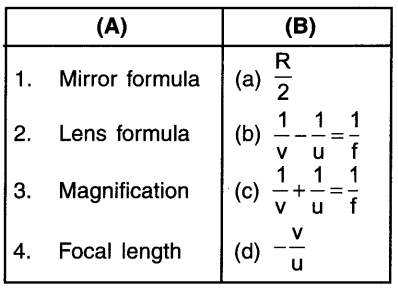
Answer:
(1-c), (2-b), (3-d), (4-a)