HBSE 10th Class Maths Solutions Chapter 9 Some Applications of Trigonometry Ex 9.1

Haryana State Board HBSE 10th Class Maths Solutions Chapter 9 Some Applications of Trigonometry Ex 9.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 9 Some Applications of Trigonometry Ex 9.1

Question 1.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (See figure).

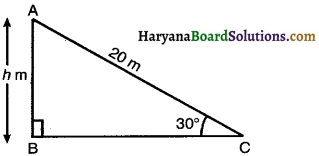
Solution :
Let height of the pole be h m.
In right ∆ABC, we have
sin 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{1}{2}=\frac{h}{20}\)
⇒ h = \(\frac{20}{2}\) = 10 m.
Hence, height of the pole is 10 m.

Question 2.
A tree breaks due to storm and the broken part bends so that top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution:
∠BDC = 30° (given)
In right ∆CBD, we have
cos 30° = \(\frac{\mathrm{BD}}{\mathrm{CD}}\)

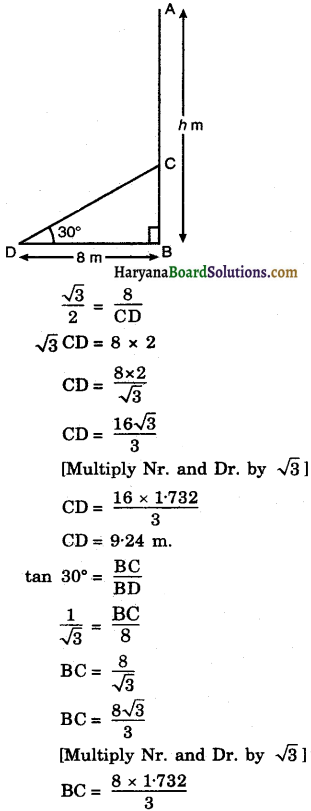
BC = 4.62
Height of the tree (h) = BC + AC
= BC + CD [∵ AC = CD]
= 462 + 924 = 1386 m.
Hence, height of the tree is 13.86 m.

Question 3.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 15 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 in, and inclined at an angle of 600 to the ground. What should be. length of the slide in each case?
Solution :
Let l₁ is the length of slide for children below the age of 5 years and l₂ is th length of the slide for elder children.

Point P represents the top of slide l₁ and inclined at an angle of 30° to the ground.
i.e., PQ = 15 m and ∠PRQ = 30°
and point A represents the top of slide l₂ and inclined at an angle of 60° to the ground.
i.e. AB = 3m and ∠ACB = 60°
In right ∆PQR, we have
sin 30° = \(\frac{\mathrm{PQ}}{\mathrm{PR}}\)
⇒ \(\frac{1}{2}=\frac{1 \cdot 5}{l_1}\)
⇒ l₁ = 2 × 1.5 = 3.o m
and in right ∆ABC, we have
sin 60° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{3}{l_2}\)
⇒ l₂ = \(\frac{3 \times 2}{\sqrt{3}}\)
⇒ l₂ = 2√3
Hence, lengths of the slides are 3m and 2√3 m.

Question 4.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from .the foot of tower, is 30°. Find the height of tower.
Solution:
Let AB be the tower of height h m and C be a point on the grourd such that angle of elevation of the top A of tower is 30°
i.e. ∠ACB = 30° and BC = 30 m.
In right ∆ABC, we have
tan 30° = \(\frac{A B}{B C}\)

h = 10√3
Hence, height of the tower is 10√3 metres.

Question 5.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution :
Let A be the position of kite.
Let C be the position of observer and AC he length of string.
Then ∠ACB = 60°,
height of kite = 60 m.
In right ∆ABC, we have

sin 60° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
\(\frac{\sqrt{3}}{2}=\frac{60}{\mathrm{AC}}\)
AC = \(\frac{60 \times 2}{\sqrt{3}}\)
AC = \(\frac{120 \sqrt{3}}{3}\)
AC = 40√3.

Hence, length of string = 40√3 metres.

Question 6.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution :
Let AB be the building of height 30 m and CD be the boy of height 15 m
i.e. AB = 30 m and CD = 15 m.
The angle of elevation from the eyes of thy to the top of building is 300 and as the boy walks towards the building the angle of elevation becomes 60°.
Then ∠ACF = 30° and ∠AEF = 60°
In right ∆AFC, we have

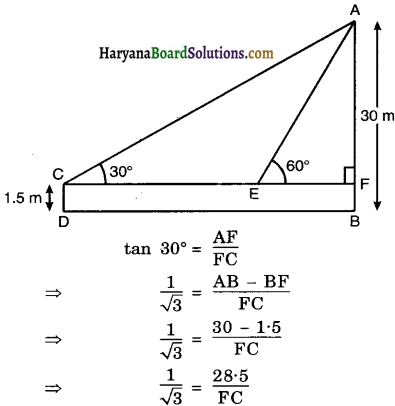
FC = 28.5√3
and in right ∆AFE, we have
[∴ AF = AB – BF = 30 – 1.5 = AF = 28.5 m]
tan 60° = \(\frac{\mathrm{AF}}{\mathrm{FE}}\)
⇒ √3 = \(\frac{28 \cdot 5}{\mathrm{FE}}\)
⇒ FE = \(\frac{28 \cdot 5}{\sqrt{3}}\)
⇒ FE = \(\frac{28 \cdot 5 \sqrt{3}}{3}\)
⇒ FE = 9.5√3
The distance walked by the boy towards the building = CE
= FC – FE
= 28.5√3 – 9.5√3 = 19√3
Hence, distance walked by the boy towards the building = 19√3 m.

Question 7.
From a point on theground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectiyely. Find the height of the tower.
Solution :
Let PQ be the transmission tower of height h m fixed at the top of 20 m heigh building (QR), angles of elevation of the bottom and top of a transmission tower are 45° and 60° respectively.
i.e. ∠QSR = 45° and ∠PSR = 60°.
In right ∆QSR, we have
tan 45° = \(\frac{\mathrm{QR}}{\mathrm{SR}}\)

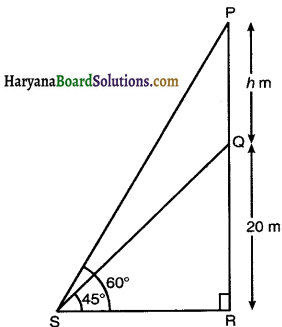
⇒ 1 = \(\frac{20}{\mathrm{SR}}\)
SR = 20 m.
In right ∆PSR, we have
tan 60° = \(\frac{\mathrm{PR}}{\mathrm{SR}}\)
√3 = \(\frac{\mathrm{PQ}+\mathrm{QR}}{20}\)
√3 = \(\frac{h+20}{20}\)
20√3 = h + 20
h = 20√3 – 20
h = 20(√3 – 1)
Hence, height of the tower is 20(√3 – 1) m.

Question 8.
A statue, 16 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution :
Let BC be the pedestal of height h m and AB be the statue.
Let D be the point of observation.
Then ∠BDC = 45°, ∠ADC = 60°, AB = 1.6 m
In right ∆BCD, we have
tan 45° = \(\frac{\mathrm{BC}}{\mathrm{CD}}\)

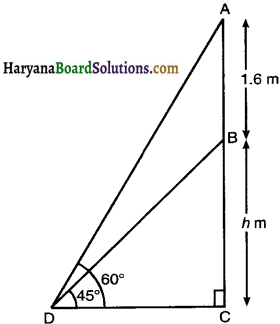
⇒ 1 = \(\frac{h}{\mathrm{CD}}\)
⇒ CD = h …………….(1)
and right ∆ACD, we have
tan 60° = \(\frac{\mathrm{AC}}{\mathrm{CD}}\)
√3 = \(\frac{\mathrm{AB}+\mathrm{BC}}{\mathrm{CD}}\)
√3 = \(\frac{1 \cdot 6+h}{h}\) [Using (1)]
√3h = 1.6 + h
√3h – h = 1.6
h(√3 – 1) = 1.6
h = \(\frac{1 \cdot 6}{\sqrt{3}-1}\)
h = \(\frac{1 \cdot 6(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}\)
[Multiplying numerator and denominator by (√3 + 1)]
h = \(\frac{1 \cdot 6(\sqrt{3}+1)}{(\sqrt{3})^2-(1)^2}\)
h = \(\frac{1 \cdot 6(\sqrt{3}+1)}{2}\)
Hence, height of pedestal is 0.8(√3 + 1) m.

Question 9.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50m high, find the height of the building.
Solution:
Let AB be tower of height 50m and PQ be the building of height h m.
The angle of elevation of the top of the tower from the foot of the building is 60° i.e. ∠AQB = 60° and angle of elevation of the top of building from the foot of the tower is 30°, i.e., ∠PBQ = 30°
In right triangle ABQ, we have
tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BQ}}\)

 

Hence, height of the building is 16\(\frac{2}{3}\) m.

Question 10.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles. [CBSE 2019]
Solution :
Let AB and CD be two poles of equal height h m, angles of elevation of the top of the poles are 60° and 30° respectively i.e. ∠AOB = 60°, ∠COD = 30° and BD = 80 m.
Let OB = x m, then DO = (80 – x) m
In right ∆ABO, we have
tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BO}}\)

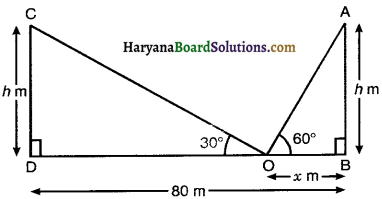
⇒ √3 = \(\frac{h}{x}\)
⇒ h = √3x
⇒ x = \(\frac{h}{\sqrt{3}}\) …………..(1)
and right ∆CDO, we have
tan 30° = \(\frac{\mathrm{CD}}{\mathrm{DO}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{80-x}\)
⇒ √3h = 80 – x
⇒ √3h = 80 – \(\frac{h}{\sqrt{3}}\) [Using (1)]
⇒ √3h + \(\frac{h}{\sqrt{3}}\) = 80
⇒ \(\frac{3 h+h}{\sqrt{3}}\) = 80
⇒ 4h = 80√3
⇒ h = \(\frac{80 \sqrt{3}}{4}\)
⇒ h = 20√3 m
Putting the value of h in (1), we get
⇒ x = \(\frac{20 \sqrt{3}}{\sqrt{3}}\)
⇒ x = 20 m.
DO = 80 – x = 80 – 20 = 60 m.
Hence height of each pole is 20√3 m and distances of point from pole (AB) is 20 m and from pole (CD) is 60 m.

Question 11.
A TV Tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. (See in figure). Find the height of tower and width of the canal.

Solution :
Let height of tower be h m. and width of canal be x m.
Then ∠ACB = 60°, ∠ADB = 30° and CD = 20 m.
In right ∆ABC, we have
⇒ tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ √3 = \(\frac{h}{x}\)
⇒ h = √3x ………………….(1)
In right ∆ABD, we have
tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{\mathrm{BC}+\mathrm{CD}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{x+20}\)
⇒ √3h = x + 20
⇒ √3 × √3x = x + 20 [Using (1)]
⇒ 3x = x + 20
⇒ 2x = 20
⇒ x = \(\frac{20}{2}\) = 10
Putting the value of x in (1), we get
h = √3 × 10
⇒ h = 10√3
Hence, height of tower is 10√3 m and width of canal is 10 m.

Question 12.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
Let AB be cable tower of height h m. and CD be building of height 7 m the angle of elevation of the top of the cable tower from the top of a building is 60°.
i.e. ∠ACE = 60° and angle of depression of its foot from the top of a building is 450
i.e. ∠ECB = 45°
∠CBD = ∠ECB [Alternate interior ∠s]
∠CBD = 45°

In right ∆AEC, we have
tan 60° = \(\frac{\mathrm{AE}}{\mathrm{CE}}\)
= \(\frac{\mathrm{AB}-\mathrm{EB}}{\mathrm{CE}}\)
= \(\frac{h-7}{\mathrm{CE}}\)
CE = \(\frac{h-7}{\sqrt{3}}\) …………….(1)
and in right ACDB, we have
tan 45° = \(\frac{\mathrm{CD}}{\mathrm{DB}}\)
1 = \(\frac{7}{\mathrm{CE}}\) [∵ DB = CE]
CE = 7
Putting the value of CE in (1), we get
7 = \(\frac{h-7}{\sqrt{3}}\)
7√3 = h – 7
7√3 + 7 = h
h = 7(√3 + 1) m.
Hence, height of cable tower is 7 (√3 + 1) m.

Question 13.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution :
Let AB be light house of height 75 m, angles of depression of two ships are 30° and 45°
i.e. ∠PAD = 30° and ∠PAC = 45°.
∠ADC = ∠PAD = 30° [alternate interior angles]
and ∠ACB = ∠PAC = 45° [alternate interior angles]
Let CD = x m.
and BC = y m.
In right ∆ABC, we have
tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ 1 = \(\frac{75}{y}\)
⇒ y = 75 m ………………(1)

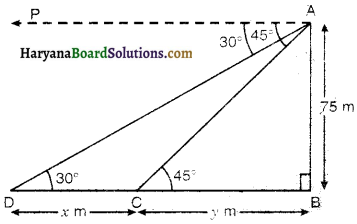
and in right ∆ABD, we have
tan 30° = \(\frac{A B}{B D}\)
\(\frac{1}{\sqrt{3}}=\frac{75}{C D-B C}\)
\(\frac{1}{\sqrt{3}}=\frac{75}{x-y}\)
x + y = 75√3
x + 75 = 75√3 [Using (1)]
x= 75√3 – 75
X= 75(√3 – 1) .
Hence, distance between the, two ships is 75(√3 – 1) m.

Question 14.
A 12 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m in from the ground. The angle of elevation of the bafloon from the eyes of the girl at any instant is 60° After s mrne, the angle of elevation reäes
to 30° (see figure). Find the distance travelled by the balloon during the interval.

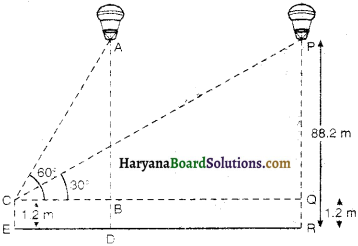
Solution :
Let A be position of balloon when its angle of elevation from eye of the girl is 60° and P he the ooition of balloon when angle of elevation is 30°. Then
∠PCQ = 30°, ∠ACB = 60° and R = 88.2 m
PQ = PR – QR = 88.2 – 1.2 = 87 m
In right ∆PQC, we have
tan 30° = \(\frac{\mathrm{PQ}}{\mathrm{QC}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{87}{\mathrm{QC}}\)
⇒ QC = 87√3 ……………….(1)
and in right ∆ABC, we have
tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ √3 = \(\frac{87}{B C}\) [∵ AB = PQ = 87 m].
⇒ BC = \(\frac{87}{\sqrt{3}}\)
⇒ BC = \(\frac{87 \sqrt{3}}{3}\) ………………..(2)
Now distance travelled by balloon = AP = BQ = QC – BC
= 87√3 – \(\frac{87 \sqrt{3}}{3}\) [From (1) and (2)]
= 87√3 (1 – \(\frac{1}{3}\))
= 87√3 × \(\frac{2}{3}\) = 58√3
Hence, distance travelled by balloon is 58√3 m.

Question 15.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution:
Let AB be vertical tower of height h m.
Let the speed of the car be v m/sec.
At the point C angle of depression of car be 30° i.e. ∠PAC = 30°
and it reaches to D six seconds later.
Then angle of depression of car is 60° i.e. ∠PAD = 60°.

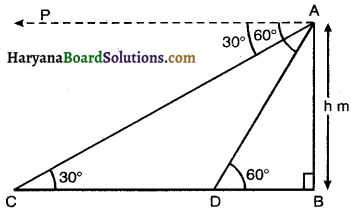
∠ACD = ∠PAC = 30° [alternate interior angles]
∠ADB = ∠PAD = 60° [alternate interior angles]
Distance travelled by car in 6 sec = 6v metres.
So, CD = 6v metres [∵ Distance = speed × time]
Let car takes t seconds to reach the point B from the point D
Distance travelled by car in t sec = vt metres.
In right ∆ABD, we have
tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
√3 = \(\frac{h}{v t}\)
⇒ h = √3vt …………………(1)
and in right ∆ABC, we have
tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{\mathrm{CD}+\mathrm{BD}}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{6 v+v t}\)
⇒ √3h = 6v + vt
⇒ √3 × √3vt = 6v + vt [Using (1)]
⇒ 3vt = 6 v + vt
⇒ 2vt = 6v
⇒ t = \(\frac{6 v}{2 v}\) = 3 sec.
Hence, the car takes 3 sec. to reach the foot of tower.

Question 16.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line With it are complementary. Prove that the height of tower is 6 m.
Solution :
Let AB be tower of height h m. C and D are two points such that BC = 9 m.
and BD = 4 m, let ∠ACB = θ then ∠ADB = 90° – θ
In right ∆ABD, we have
tan (90° – θ) = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)

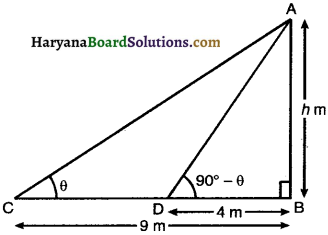
⇒ cot θ = \(\frac{h}{4}\)
[∵ tan (90° – θ) = cot θ]
⇒ h = 4 cot θ ………………(1)
In right ∆ABC, we have
tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
tan θ = \(\frac{h}{9}\)
⇒ h = 9 tan θ ………………(2)
Multiplying (1) & (2), we get
h × h = 4 cot θ . 9 tan θ
⇒ h² = 4 × \(\frac{1}{\tan \theta}\) × 9 tan θ
⇒ h² = 36
⇒ h = √36 = 6
Hence, height of tower is 6 m.
Hence Proved.