HBSE 10th Class Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1

Haryana State Board HBSE 10th Class Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1

Question 1.
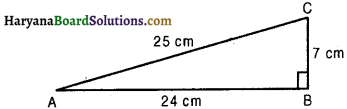
In ∆ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine :
(i) sin A, cos A
(ii) sin C, cos C
Solution :
(i) In a right’triangle ABC we have ∠B = 90°, AB = 24 cm and BC = 7 cm.
By Pythagoras theorem, we have
AC² = AB² + BC²
⇒ AC² = 242 + 72
⇒ AC² = 576 + 49
⇒ AC² = 625
⇒ AC = \(\sqrt{625}\) = 25

∴ sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{25}\)
cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24}{25}\)
Here, sin A = \(\frac{7}{25}\), cos A = \(\frac{24}{25}\)

(ii) For trigonometric ratio of ∠C, We have base = BC = 7 cm
Perpendicular = AB = 24 cm
Hypotenuse = AC = 25 cm
sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24}{25}\)
and cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{25}\)
Hence, sin C = \(\frac{24}{25}\), cos C = \(\frac{7}{25}\)

Question 2.
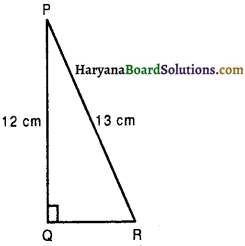
In figure, find tan P – cot R.

Solution:
We have, PQ = 12 cm, PR = 13 cm.
In right ∆PQR, ∠Q = 90°
By Pythagoras theorem, we have PR² = QR² + PQ²
⇒ (13)² = QR² + (12)²
⇒ QR² = (13)² – (12)²
⇒ QR² = (13 + 12) (13 – 12)
⇒ QR² = 25
⇒ QR = √25 = 5
cot R = \(\frac{\mathrm{QR}}{\mathrm{PQ}}=\frac{5}{12}\)
For trigonometric ratio of ∠P, we have
Base = PQ = 12 cm
Perpendicular = QR = 5 cm
Hypotenuse = PR = 13 cm
∴ tan P = \(\frac{\mathrm{QR}}{\mathrm{PQ}}=\frac{5}{12}\)
Now, tan P – cot R = \(\frac{5}{12}-\frac{5}{12}\) = 0
Hence, tan P – cot R = 0.

Question 3.
If sin A = \(\frac{3}{4}\) Calculate cos A and tan A.
Solution :
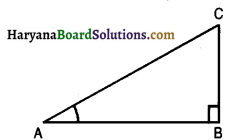
Consider a right triangle ABC in which ∠B = 90°
Then, sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}\)
Let BC = 3k and AC = 4k, where k is a positive integer.
By Pythagoras theorem, we have

AC² = AB² + BC²
(4k)² = AB² + (3k)²
AB² = (4k)² – (3k)²
AB² = 16k² – 9k²
AB² = 7k²
AB = √7 k
∴ cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{7} k}{4 k}=\frac{\sqrt{7}}{4}\)
and tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3 k}{\sqrt{7} k}=\frac{3}{\sqrt{7}}\)
Hence, cos A = \(\frac{\sqrt{7}}{4}\), tan A = \(\frac{3}{\sqrt{7}}\).

Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution :

we have,
15 cot A = 8
cot A = \(\frac{8}{15}\)
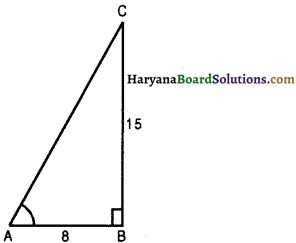
Now consider a right 15 triangle ABC, in which ∠B = 90°
cot A = \(\frac{8}{15}\)
⇒ \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{8}{15}\)
Let AB = 8k and BC = 15k,where k is a positive integer.
By Pythagoras theorem, we have
AC² = AB² + BC²
AC² = (8k)² + (15k)²
AC² = 64k² + 225k²
AC = 289k²
AC = \(\sqrt{289 k^2}\) = 17k.
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}:=\frac{15 k}{17 k}=\frac{15}{17}\)
and sec A = \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{17 k}{8 k}=\frac{17}{8}\)
Hence, sin A = \(\frac{15}{17}\) and sec A = \(\frac{17}{8}\).

Question 5.
Given sec θ = \(\frac{13}{12}\), calculate all other trigonometric ratios.
Solution:
Consider a right triangle ABC in which ∠B = 90°, ∠CAB = 9, sec θ = \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{13}{12}\)
Let AC = 13k and AB = 12k, where k is a positive integer.

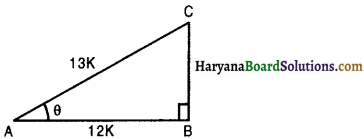
By Pythagoras theorem, we have
AC² = AB² + BC²
(13k)² = (12k)² + BC²
BC² = (13k)² – (12k)²
BC² = (13k + 12k) (13k – 12k)
BC² = 25k × k = 25k²
BC = \(\sqrt{25 k^2}\) = 5k

∴ sin θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{5 k}{13 k}=\frac{5}{13}\)
cos θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{12 k}{13 k}=\frac{12}{13}\)
tan θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{5 k}{12 k}=\frac{5}{12}\)
cot θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{12 k}{5 k}=\frac{12}{5}\)
cosec θ = \(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{13 k}{5 k}=\frac{13}{5}\)

Hence, sin θ = \(\frac{5}{13}\),
cos θ = \(\frac{12}{13}\),
tan θ = \(\frac{5}{12}\),
cot θ = \(\frac{12}{5}\),
cosec θ = \(\frac{13}{5}\).

Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B; then show that ∠A = ∠B.
Solution :
Let us consider right triangle ABC in which ∠C = 90° and cos A = cos B.
Draw CD ⊥ AB.
In right triangle ADC, ∠ADC = 90°.
cos A = \(\frac{\mathrm{AD}}{\overline{\mathrm{AC}}}\) ………………….(1)
In right ∆BDC,
∠BDC = 90°
cos B = \(\frac{\mathrm{BD}}{\overline{\mathrm{BC}}}\) ………………….(2)

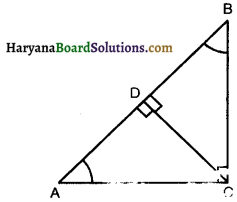
According to question,
cos A = cos B
\(\frac{\mathrm{AD}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{BC}}\)
\(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{AC}}{\mathrm{BC}}\) [each = \(\frac{C D}{C D}\)]
∆ADC ~ ∆BDC [By SSS similarity criterion]
[corresponding ∠s of two similar ∆s are equal]
Hence Proved.

Question 7.
If cot θ = \(\frac{7}{8}\), evaluate:
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot² θ
Solution :

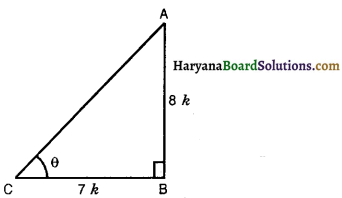
(i) Consider a triangle ABC in which ∠B = 90°,
∠ACB = θ and cot θ = \(\frac{7}{8}\)
⇒ \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{7}{8}\)
Let BC = 7k and AB = 8k, where k is a positive integer,
By Pythagoras theorem, we have
AC² = BC² + AB²
AC² = (7k)² + (8k)²
AC² = 49k² + 64k²
AC² = 113k²
AC = √113 k
∴ sin θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{8 k}{\sqrt{113} k}=\frac{8}{\sqrt{113}}\)

(ii) cot² θ = (cot θ)²
= \(\left(\frac{\mathrm{BC}}{\mathrm{AB}}\right)^2=\left(\frac{7 k}{8 k}\right)^2\)
= \(\left(\frac{7}{8}\right)^2=\frac{49}{64}\)

Hence, (i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}=\frac{49}{64}\)
(ii) cot² θ = \(\frac{49}{64}\)

Question 8.
If 3 cot A = 4, check whether \(\frac{1-\tan ^2 \mathrm{~A}}{1+\tan ^2 \mathrm{~A}}\) = cos² A – sin² A or not.
Solution :
Consider a triangle ABC in which ∠B = 90° and 3 cot A = 4
⇒ cot A = \(\frac{4}{3}\)
⇒ \(\frac{A B}{B C}=\frac{4}{3}\)
Let AB = 4k and BC = 3k,where k is a positive integer.

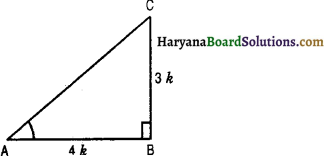
By pythagoras theorem, we have
AC² = AB² + BC²
⇒ AC² = (4k)² + (3k)²
⇒ AC² = 16k² + 9k²
⇒ AC² = 25k²
⇒ AC = \(\sqrt{25 k^2}\)
⇒ AC = 5k

Hence, \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos² A – sin² A.

Question 9.
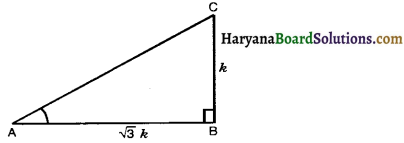
In triangle ABC, right angled at B, if tan A = find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:
In right triangle ABC, ∠B = 90° and tan A = \(\frac{1}{\sqrt{3}}\)
\(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\)
Let BC = k and AB = √3k,where k is positive integer.

By pythagoras theorem, we have
AC² = AB² + BC²
AC² =(√3k)² + k²
AC² = 3k² + k² = 4k²
AC = \(\sqrt{4 k^2}\) = 2k
∴ sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)
and cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)
Now, for trigonometric ratio of ∠C, we have
Base = BC = k
Perpendicular = AB = √3 k
Hypotenuse = AC = 2k
sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)
cosC = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)

(i) sin A cos C + cos A sin C = \(\frac{1}{2} \times \frac{1}{2}+\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}\)
= \(\frac{1}{4}+\frac{3}{4}=\frac{4}{4}\) = 1

(ii)cos A cos C – sin A sinC= \(\frac{\sqrt{3}}{2} \times \frac{1}{2}-\frac{1}{2} \times \frac{\sqrt{3}}{2}\)
= \(\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4}\) = 0

Hence, (i) sin A cos C + cos A sin C = 1
(ii) cos A cos C – sin A sin C = 0.

Question 10.
In ∆PQR, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:
In right ∆PQR, ∠Q = 90°, PQ = 5 cm and PR + QR = 25 cm

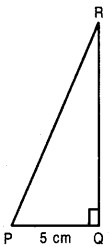
⇒ PR = 25 – QR
By Pythagoras theorem, we have
PR² = PQ² + QR²
(25 – QR)² = (5)² + QR²
⇒ 625 + QR² – 50 QR = 25 + QR²
⇒ QR² – 50QR – QR² = 25 – 625
⇒ – 50 QR = – 600
⇒ QR = \(\frac{-600}{-50}\) = 12 cm
and PR = 25 – 12 = 13 cm
∴ sin P = \(\frac{\mathrm{QR}}{\mathrm{PR}}=\frac{12}{13}\)
cos P = \(\frac{\mathrm{PQ}}{\mathrm{PR}}=\frac{5}{13}\)
tan P = \(\frac{\mathrm{QR}}{\mathrm{PQ}}=\frac{12}{5}\)
Hence, sin P = \(\frac{12}{13}\), cos P = \(\frac{5}{13}\) and tan P = \(\frac{12}{5}\).

Question 11.
State whether the following are true or false. Justify your Answer.
(i) The value of tan A is always less than 1.
(ii) sec A = \(\frac{12}{5}\) for some value of ∠A.
(iii) cos A is the abbreviation used, for the cosecant of ∠A.
(iv) cot A is the product of cot and A.
(v) sin θ = \(\frac{4}{3}\) for some angle θ.
Solution :
(i) False. Because tan 60° = √3 > 1
(ii) True. Because value of sec A is always ≥ 1.
(iii) False. Because cos A is abbreviation used for cosine A.
(iv) False. Because cot is meaningless without an angle.
(v) False. Because sin θ > 1.