HBSE 10th Class Maths Solutions Chapter 6 Triangles Ex 6.4

Haryana State Board HBSE 10th Class Maths Solutions Chapter 6 Triangles Ex 6.4 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 6 Triangles Ex 6.4

Question 1.
Let ∆ABC ~ ∆DEF and their areas be respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution :
We have, ∆ABC ~ ∆DEF

Hence, BC = 11.2 cm.

Question 2.
Diagonals of trapezium ABCD with AB || CD intersects each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.

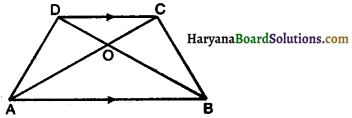
Solution:
We have, AB || CD and AB = 2CD
In triangles AOB and COD,
∠ABO = ∠CDO (alternate interior ∠s)
∠AOB = ∠COD (vertically opposite ∠s)
∆AOB ~ ∆COD (By AA similarity criterion)
⇒ \(\frac{\ {ar}(\Delta \mathrm{AOB})}{\ {ar}(\Delta \mathrm{COD})}=\frac{\mathrm{AB}^2}{\mathrm{CD}^2}\)
⇒ \(\frac{\ {ar}(\triangle \mathrm{AOB})}{\ {ar}(\triangle \mathrm{COD})}=\frac{(2 \mathrm{CD})^2}{\mathrm{CD}^2}\)
⇒ \(\frac{\ {ar}(\triangle \mathrm{AOB})}{\ {ar}(\triangle \mathrm{COD})}=\frac{4 \mathrm{CD}^2}{\mathrm{CD}^2}\)
⇒ \(\frac{\ {ar}(\triangle \mathrm{AOB})}{\ {ar}(\triangle \mathrm{COD})}=\frac{4}{1}\)
Hence, ar(∆AOB) : ar(∆COD) = 4 : 1.

Question 3.
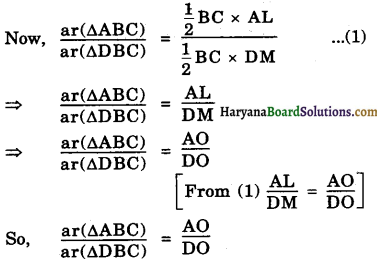
In given figure ABC and DBC are two triangles on the same base BC.. If AD intersects BC at O, show that \(\frac{\ {ar}(\triangle \mathrm{ABC})}{\ {ar}(\triangle \mathrm{DBC})}=\frac{\mathrm{AO}}{\mathrm{DO}}\).

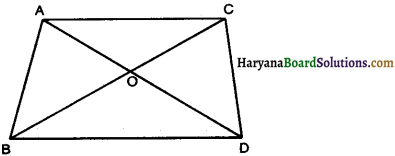
Solution :
Given : ∆ABC and ∆DBC are two triangles on the same base BC
To Prove: \(\frac{\ {ar}(\triangle \mathrm{ABC})}{\ {ar}(\triangle \mathrm{DBC})}=\frac{\mathrm{AO}}{\mathrm{DO}}\)
Construction : Draw AL ⊥ BC and DM ⊥ BC
Proof : In ∆ALO and ∆DMO

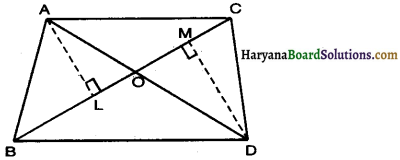
∠ALO = ∠DMO = 90° (By construction)
∠AOL = ∠DOM (vertically opposite ∠s)
∆ALO ~ ∆DMO (By AA similarity criterion)
⇒ \(\frac{\mathrm{AL}}{\mathrm{DM}}=\frac{\mathrm{AO}}{\mathrm{DO}}\)
[corresponding sides of similar triangles are proportional]

Hence proved.

Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:
Given : Let two triangles ABC and PQR such that ar(ABC) = ar(APQR)
To Prove: ∆ABC ∆PQR
Proof: ar(∆ABC) ≅ ar(∆PQR)
⇒ ∆ABC ~ ∆PQR
⇒ ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R
and \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{CA}}{\mathrm{RP}}\)

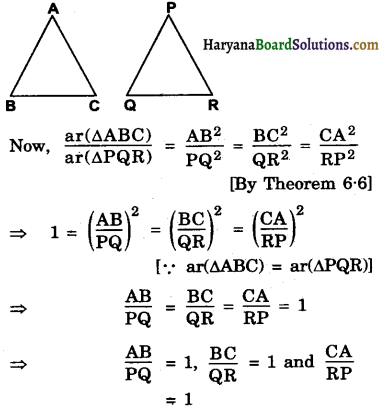
⇒ AB = PQ, BC = QR, CA = RP
∴ ∆ABC ≅ ∆PQR (By SSS congruence criteriah)
Hence Proved.

Question 5.
D, E and F are respectively the mid points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution:
We have,
∵ D, E and F, are the mid points of sides AB, BC and CA respectively.
∴ DF = \(\frac{1}{2}\)BC, DE = \(\frac{1}{2}\)AC and EF = \(\frac{1}{2}\)AB
[Mid point Theorem]

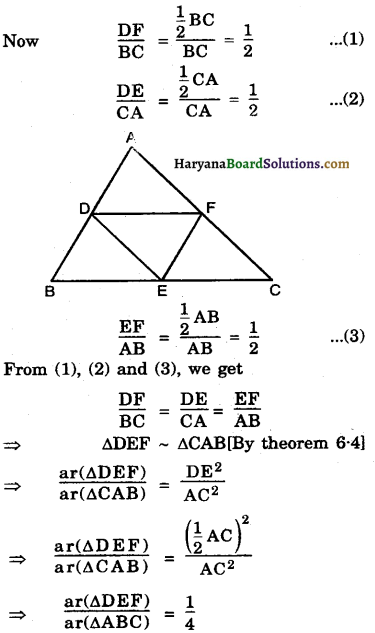
Hence, ar(∆DEF) : ar(∆ABC) = 1 : 4.

Question 6.
Prove that ratio of the areas of two similar triangles is equal to square of the ratio of their corresponding medians.
Solution:
Given: Two triangles ABC and PQR such that AABC – APQR and AD, PM are their medians respectively.

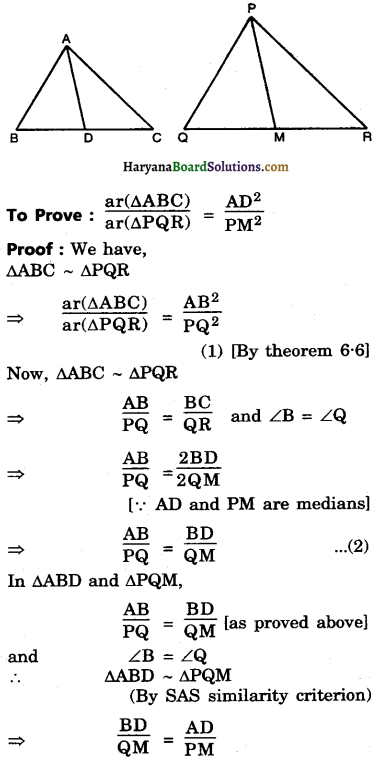
Hence proved.

Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution :
Given : A square ABCD and two equilateral ∆s BCE and ACF have been described on side BC and diagonal AC respectively.
To Prove: Area (∆BCE) = \(\frac{1}{2}\) Area (∆ACF)
Proof: We have ∆BCE and ∆ACF are equilateral triangles.

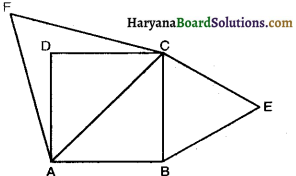
∠B = ∠A (each = 60°)
∠C = ∠C (each = 60°)
∠E = ∠F (each = 60°)
∆ BCE ~ ∆ ACF (By AAA similarity criterion)
⇒ \(\frac{\ {ar}(\triangle \mathrm{BCE})}{\ {ar}(\triangle \mathrm{ACF})}=\frac{\mathrm{BC}^2}{\mathrm{AC}^2}\)
[By theorem 6.6] ………………..(1)
But AB = BC (sides squares)
and AC² = AB² + BC² [By Pythagoras theorem]
⇒ AC² = 2BC² ……………..(2)
From (1) and (2), we get
\(\frac{\ {ar}(\Delta B C E)}{\ {ar}(\Delta A C F)}=\frac{B^2}{2 B C^2}\)
⇒ \(\frac{\ {ar}(\triangle B C E)}{\ {ar}(\triangle A C F)}=\frac{1}{2}\)
⇒ ar(∆BCE) = \(\frac{1}{2}\) ar(∆ACF)
Hence Proved.

In question 8 and 9, tick the correct answer and justify:
Question 8.
ABC and BDE are two equilateral triangles such that D is the mid point of BC. Ratio of the areas of ∆ABC and ∆BDE is :
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
Solution :
Correct answer is (C).
Justification : ∆ABC and ∆BDE are two equilateral triangles.
Let AB = BC = CA = a unit
Then BD = \(\frac{a}{2}\) unit
[∵ D is the mid point of BC]
∵ ∠CAB = ∠DBE, ∠ABC = ∠BDE, ∠ACB = ∠BED [each is 60°]
∆ABC ~ ∆BDE (By AAA similarity criterion)
⇒ \(\frac{\ {ar}(\triangle \mathrm{ABC})}{\ {ar}(\Delta \mathrm{BDE})}=\frac{\mathrm{AB}^2}{\mathrm{BD}^2}\) [By theorem (6.6)]

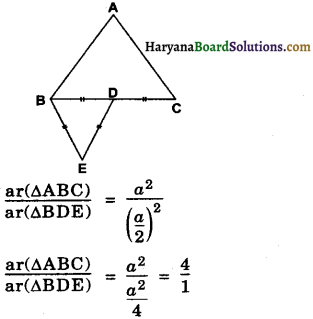
⇒ ar(∆ABC) : ar(∆BDE) = 4 : 1.

Question 9.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Solution :
Correct answer is (D).
Justification : We have,
\(\frac{\text { Side of } 1^{\text {st }} \text { triangle }}{\text { Side of } 2^{\text {nd }} \text { triangle }}=\frac{4}{9}\)
We know that areas of two similar triangles are in the ratio of the squares of their corresponding sides.
∴ \(\frac{\text { Area of Ist triangle }}{\text { Area of IInd triangle }}=\frac{(\text { side of } 1 \text { st } \Delta)^2}{(\text { side of } 2 \text { nd } \Delta)^2}\)
⇒ \(\frac{\text { Area of Ist triangle }}{\text { Area of IInd triangle }}=\frac{4^2}{9^2}\)
⇒ \(\frac{\text { Area of Ist triangle }}{\text { Area of IInd triangle }}=\frac{16}{81}\)
⇒ Area of 1st triangle : Area of IInd triangle = 16 : 81.