Haryana State Board HBSE 10th Class Maths Notes Chapter 11 Constructions Notes.
Haryana Board 10th Class Maths Notes Chapter 11 Constructions
Introduction
In class IX, we have learnt about some constructions namely drawing the perpendicular bisector of a line segment, bisecting an angle, some constructions of triangles also gave their justifications In this chapter we shall study some more constructions by using the knowledge of the earlier constructions e.q. division of a line segment drawing a triangle similar to a given triangle and drawing of tangents to a circle.
Division of a line Segment
First of all, we will know about some basic terms.
1. Construction: The process or art of constructing, OR the act of devising and forming.
2. Similar: Two geometrical figures are similar if they are of the same shape but not necessarily of the same size.
3. Bisect: To divide into two equal parts.
4. Arc: The part of a curve between two given points on the curve.
5. Altitude: A line through one vertex of a triangle and perpendicular to the opposite side.
6. Tangent: It is a straight line which touches the circle at one point only
7. Point of Contact: The point at which the tangent touches the circle is called the point of contact
8. Concentric circles: Two circles are known as concentric circles, if they have some centre and different radii.
9. Corresponding : (i) Similar in character, form or function.
(ii) Able to be matched, joined or interlocked.
![]()
Construction 1:
To divide a line segment in a given ratio
Given a line segment AB, we want to divide it in the ratio m : n here m and n are positive integers. We take m = 2, n = 3.
Steps of Construction:
1. Draw any ray AX, making an acute angle with AB.
2. Along AX mark (2 + 3) = 5 points A1, A2, A3, A4 and A5 such that AA1 = A1A2 = A2A3 = A3A4 = A4A5.
3. Join A5B.
4. From the point A2 draw A2C || A5B, meeting AB at C. Then AC : BC = 2 : 3.
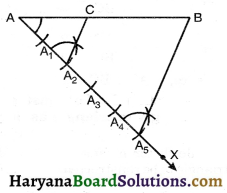
Justification: In ΔACA2 and ΔABA5 we have CA2 || BA5
\(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{AA}_2}{\mathrm{~A}_2 \mathrm{~A}_5}\)
[By Basic proportionality theorem]
\(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{2}{3}\)
Hence, AC : BC = 2 : 3.
Alternative Method:
Steps of Construction:
1. Draw a line segment AB.
2. Draw a ray AX making an acute angle with AB.
3. Draw a ray BY (On opposite side of AX) parallel to AX making ∠ABY = ∠BAX.
4. Along AX mark the points A1, A2 and along By mark the points B1, B2, B3 such that AA1 = A1A2 = BB1 = B1B2 = B2B3.
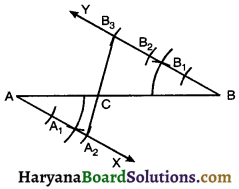
5. Join A2B3 intersecting AB at point C. Then
AC : BC = 2 : 3.
Justification: Here, AX || BY
∠CAX = ∠ABY (Alternate interior ∠S)
∠ACA2 = ∠BCB3 (Vertically opposite ∠S)
ΔCAA2 ~ ΔCBB3 (By AA similarity criterian)
⇒ \(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{AA}_2}{\mathrm{BB}_3}\)
⇒ \(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{2}{3}\)
Hence, AC : BC = 2 : 3.
Construction 2:
To construct a triangle similar to a given triangle as per given scale factor.
Scale factor means the ratio of the sides of the triangle to be constructed with the corresponding sides of the given triangle e.g.
1. Scale factor \(\frac{2}{3}\) means the sides of the constructed triangle is \(\frac{2}{3}\) of the sides of given triangle.
2. Scale factor \(\frac{5}{4}\) means the sides of the constructed triangle is \(\frac{5}{4}\) of sides of given triangle.
Let us take the following examples for understanding the construction involved.
![]()
Construction of Tangents to a Circle
We study in circles (Chapter-10) that tangent to circle is a line that intersects the circle at only one point. The point is called the point of contact. The tangent at any point of a circle is perpendicular to the radius through the point of contact.
(a) Construction of Tangents to a Circle from a point outside the circle when its centre is known:
Steps of Construction:
1. Draw a Circle with centre O and given radius.
2. Mark a point P outside the circle.
3. Join OP and draw perpendicular bisector of PO meeting PO at M.
4. Draw a circle with M as centre and radius equal to PM = OM. intersecting the given circle at points Q and R.
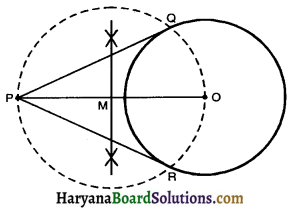
5. Join PQ and PR.
Then PQ and PR are the required tangents.
(b) Construction of Tangents to a circle from a point outside the circle when the centre of circle is not known:
Steps of Construction:
1. Taking three points A, B, C on the circle and join AB and BC.
2. Draw perpendicular bisectors of AB and BC which intersect each other at point O.
3. Then O is the required centre of the given circle.
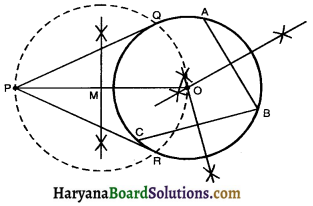
4. Mark a point P outside the circle.
5. Join PO and draw perpendicular bisector of PO meeting PO at M.
6. M as the centre, PM = MO as the radius draw another circle which intersects the previous circle at the points Q and R.
7. Join PQ and PR.
Then PQ and PR are the required tangents.