Haryana State Board HBSE 10th Class Maths Notes Chapter 10 Circles Notes.
Haryana Board 10th Class Maths Notes Chapter 10 Circles
Introduction
We have studied in class IX that a circle is a collection of all the points in a plane which are at a constant distance from a fixed point. The constant distance is called the radius and fixed point is known as the centre. We have also studied various terms related to a circle like chord, sector, segment, arc etc.
In this chapter we shall learn about tangents to a circle and some of their properties. Let us now examine the different situations that can arise when a line and a circle are given in a plane.
Tangent of a circle
Consider a circle with centre O and a line P in the plane of the circle. There are three types of possibilities arise as shown in the figures below:
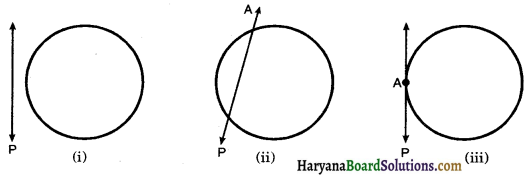
In the figure (i), the line P and the circle have no common point hence, the line P is known as a non intersecting line with respect to the circle.
In the figure (ii), the line P intersects the circle in two distinct points A and B. It is called a secant of the circle.
In the figure (iii), the line P intersects the circle in one and only one point A and is said to be a tangent to the circle. The point A at which the tangent line meets the circle is called the Point of contact.
Normal: The line containing the radius through the point of contact is also sometimes called the normal to the circle at the point.
Supplementary angles: Two angles having sum 180° are called supplementary angles.
Co-interior angles: Interior angles on the same side of the transversal are called co-interior angles or consecutive interior angles.
Concentric circles: Circles having the same centre are called concentric circles.
Parallelogram: A quadrilateral having each pair of opposite sides equal and parallel is called parallelogram.
Rhombus : A parallelogram having all the sides equal is called a rhombus.
Circumscribed circle: The circumscribed circle or circumcircle of a polygon is a circle passing through all the vertices of the polygon. The centre of this circle is called circumcentre and its radius is called the circumradius.
Inscribed circle: Inscribed circle or incircle of a polygon is the largest circle that can be contained in the polygon and it touches each side of the polygon at a point. Hence each side of the polygon is a tangent to the incircle. The centre of this circle is called incentre and its radius is called inradius.
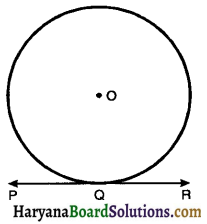
A line which intersects the circle at only one point is known as the tangent to the circle. In the given figure PQR is a tangent to the circle and point Q is the point of contact.
![]()
The word tangent to a circle has been derived from the latin word “Tangere”, which means ‘to touch’ and was introduced by the Denish mathematician Thomas Fineke in 1583.
The tangent to a circle is a special case of the secant, when the two end points of its chord coincide.
Some Properties of tangent to a circle
Theorem 10.1:
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: A circle with centre O and a tangent AB to the circle at a point P.
To Prove: OP ⊥ AB.
Construction: Take any point R, other than P on the tangent AB. Join OR. Suppose OR meets the circle at Q.
Proof :
OP = OQ (Radii of the same circle)
But OP < OQ + QR
OP < OR
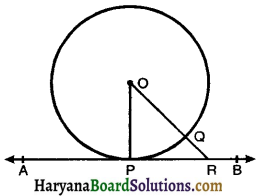
Thus, OP is shorter than any other line segment joining O to any point of AB, other than P.
We know that among all line segment joining the point O to a point on AB, the shortest one is perpendicular to AB.
Hence, OP ⊥ AB. Proved
![]()
Number of Tangents from a point on a circle
To get an idea of the number of tangents from a joint on a circle, let us perform the following activity:
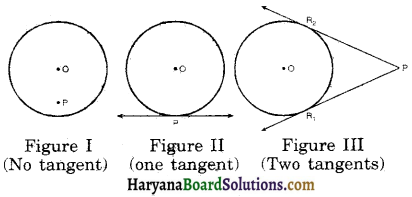
From figure (III) PR1 and PR2 are two tangents drawn from a point P lying outside the circle. These tangents touch the circle at R1 and R2 respectively. So, R1 and R2 are called points of contact of tangenta PR1 and PR2.
(i) There is no tangent to a circle passing through a point lying inside the circle.
(ii) There is one and only one tangent to a circle passing through a point lying on the circle.
(iii) There are exactly two tangents to a circle through a point lying outside the circle.
Length of Tangent: The length of segment of the tangent from the external point P and point of contact with the circle is called the length of the tangent from the point P to the circle.
From figure (III), PR1 and PR2 are the length of tangents from P to the circle.
Theorem 10.2:
The lengths of tangents drawn from an external point to a circle are equal.
Given: AP and AQ are two tangents from a point A to a circle C (O, r).
To Prove: AP = AQ
Construction: Join OA, OP and OQ.
Proof: AP is a tangent at P and OP is the radius through P.
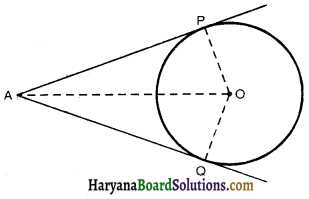
Similarly AQ is a tangent at Q and OQ is the radius through Q.
∴ OQ ⊥ AQ
In the right ΔOPA and ΔOQA, we have
OP = OQ [equal radii of the same circle]
AO = AO [common]
∠OPA = ∠OQA [each is 90°]
∴ ΔOPA ≅ ΔOQA [By RHS congruence]
⇒ AP = AQ [By CPCT Proved]
Hence, AP = AQ. Proved