Haryana State Board HBSE 9th Class Maths Notes Chapter 8 Quadrilaterals Notes.
Haryana Board 9th Class Maths Notes Chapter 8 Quadrilaterals
Introduction
In previous chapters 6 and 7, we have studied about triangles and their properties. We know that figure obtained by joining three non-collinear points in pairs, is a triangle. If we have four points in a plane such that no three of them are collinear.
If we joined these points, we obtain a figure with four sides (see figure 8.1).

Key Words
→ Intercept: To cut off.
→ Internal bisector: Name sometimes given to the bisector of the interior angle of a triangle (or polygon).
→ External bisector: The bisector of the exterior angle of a triangle (or polygon) is sometimes called the external bisector of the angle of the triangle (or polygon).
![]()
Basic Concepts
1. Quadrilateral: A closed figure which bounded by four line segments is called quadrilateral. Figure 8.2 represents a quadrilateral with vertices A, B, C and D. It is denoted by the symbol quad. ABCD or ☐ABCD.
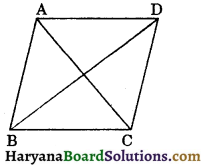
Four straight lines AB, BC, CD and DA are called the sides of the quadrilateral ABCD and ∠A, ∠B, ∠C and ∠D are the four angles of it.
The straight lines joining the opposite vertices of a quadrilateral are called its diagonals. Thus, a quadrilateral ABCD has two diagonals; namely AC and BD.
In a quadrilateral, we have the following definitions:
(a) Consecutive or adjacent sides: Two sides with common vertex are called the adjacent sides. In fig. 8.2 AB and BC, BC and CD, CD and DA and DA and AB are four adjacent sides of the quadrilateral ABCD.
(b) Opposite sides: Two sides of a quadrilateral having no common end point are called its opposite sides.
In fig. 8.2, AB and CD, AD and BC are two pairs of opposite sides of quad. ABCD.
(c) Consecutive angles: Two angles of a quadrilateral having a common side are called its consecutive angles.
In fig. 8.2, ∠A and ∠B, ∠B and ∠C, ∠C and ∠D and ∠D and ∠A are four pairs of consecutive angles of ☐ABCD.
(d) Opposite angles: Two angles of a quadrilateral having no common side are called its opposite angles.
In figure 8.2, ∠A and ∠C, ∠B and ∠D are two pairs of opposite angles of ☐ABCD.
2. Angle Sum Property of a Quadrilateral:
Let us now recall the angle sum property of a quadrilateral. The sum of the angles of a quadrilateral is 360°. This can be verified by drawing a diagonal and dividing the quadrilateral into two triangles.
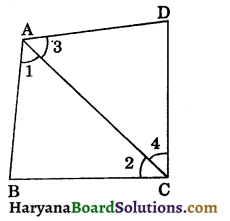
Let ABCD be a quadrilateral and AC be a diagonal (see figure 8.3).
In ΔABC, we have
∠1 + ∠B + ∠2 = 180°…(1)
I. Sum of interior angles of a triangle 180°]
In ΔADC, we have
∠3 + ∠D + ∠4 = 180°…(ii)
Adding (i) and (ii), we get
∠1 + ∠3 + ∠B + ∠2 + ∠4 + ∠D = 180° + 180°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
[∵ ∠1 + ∠3 = ∠A and ∠2 + ∠4 = ∠C]
Hence, sum of angles of a quadrilateral is 360°.
![]()
3. Types of Quadrilaterals:
(i) Trapezium: A quadrilateral in which one pair of opposite sides is parallel but the other pair of opposite sides is non-parallel is called a trapezium.
The figure 8.4, represents a trapezium ABCD.
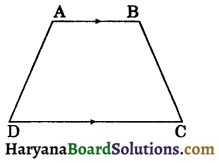
In which AB || CD and AD and BC are non-parallel sides. If the non-parallel sides AD and BC of the trapezium are equal, it is called an isosceles trapezium. In this case, ∠D = ∠C and ∠A = ∠B.
(ii) Parallelogram: A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram.

The figure 8.5, represents a parallelogram ABCD, since AD || BC and AB || CD.
(iii) Rectangle: A parallelogram in which each angle is a right angle is called a rectangle.
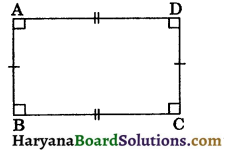
The figure 8.6, represents a rectangle ABCD in which ∠A = ∠B = ∠C = ∠D = 90°.
(iv) Square: A parallelogram in which all sides are equal and each angle is equal to 90° is called a square.
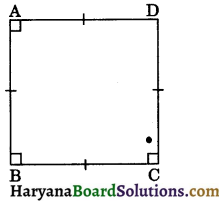
The figure 8.7, represents a square ABCD in which AB = BC = CD = DA and ∠A = ∠B = ∠C = ∠D = 90°.
(v) Rhombus: A parallelogram in which all sides are equal is called a rhombus.

The figure 8.8, represents a rhombus. ABCD in which AB = BC = CD = DA.
(vi) Kite: A quadrilateral in which both pairs of adjacent sides are equal is called a kite.
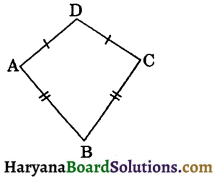
The figure 8.9, represents a kite ABCD in which AD = DC and AB = BC.
Note:
(i) Every parallelogram is a trapezium but every trapezium is not a parallelogram.
(ii) Every square is a rectangle and also a rhombus but every rectangle or rhombus is not a square.
(iii) A kite is not a parallelogram.
(iv) Every square, rectangle and rhombus are parallelograms.
![]()
4. Properties of a Parallelogram:
Theorem 8.1:
A diagonal of a parallelogram divides it into two congruent triangles.
Given: ABCD is a parallelogram and AC its diagonal.
To prove :
ΔABC ≅ ΔCDA.
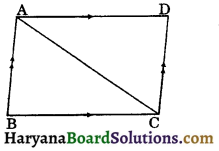
Proof: ABCD and AC cuts them
∠BAC = ∠DCA …..(i)
(Alternate interior angles)
and BC || AD and AC cuts them.
∠BCA = ∠DAC (Alternate interior angles)
Now, in ΔABC and ΔCDA, we have
∠BAC = ∠DCA, [From (i)]
AC = AC, (Common)
and ∠BCA = ∠DAC, [From (ii)]
ΔABC ≅ ΔCDA [By ASA congruence rule]
Hence proved
Theorem 8.2:
In a parallelogram, opposite sides are equal.
Given: ABCD is a parallelogram.
To prove: AB = CD and AD = BC.
Construction: Join AC.
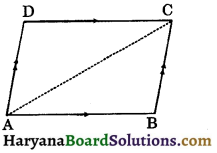
Proof: ABDC and AC cuts them.
∠BAC = ∠DCA …(i) (Alternate interior angles)
Again AD || BC and AC cuts them.
∠BCA = ∠DAC …(ii)
(Alternate interior angles).
Now, in AABC and ACDA, we have
∠BAC = ∠DCA, [From (i)]
AC = AC, [Common]
and ∠BCA = ∠DAC, [From (ii)]
ΔABC ≅ ΔCDA (By ASA congruence rule)
AB = CD and AD = BC, (CPCT)
Hence proved
Theorem 8.3:
If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Given: A quadrilateral ABCD in which AB = CD and BC = DA.
To prove: Quadrilateral ABCD is a parallelogram.
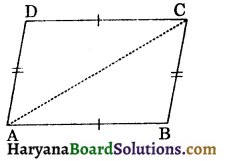
Construction: Join AC.
Proof: In ΔABC and ΔCDA, we have
AB = CD, (Given)
BC = AD, (Given)
and AC = AC, (Common)
ΔABC ≅ ΔCDA (By SSS congruence rule)
⇒ ∠BAC = ∠DCA, (CPCT)
⇒ AB || CD …..(i)
and ∠BCA = ∠DAC, (CPCT)
AD || BC …..(ii)
From (i) and (ii), we get
AB || CD and AD || BC
Hence, ABCD is a parallelogram. Hence Proved
![]()
Theorem 8.4:
In a parallelogram, opposite angles are equal.
Given: ABCD is a parallelogram.
To prove: ∠A = ∠C and ∠B = ∠D.
Proof : BC || AD and AB cuts them.
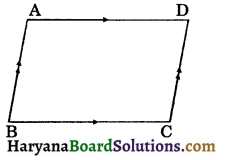
⇒ ∠A + ∠B = 180° …(1)
[Sum of co-interior angles is 180°]
Again, AB || CD and AD intersects them.
⇒ ∠A + ∠D = 180° …..(ii)
[Sum of co-interior angles is 180°]
From (i) and (ii), we get
∠A + ∠B = ∠A + ∠D
⇒ ∠B = ∠D
Similarly, ∠A = ∠C.
Hence proved
Theorem 8.5:
If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Given: A quadrilateral ABCD in which ∠A = ∠C and ∠B = ∠D.
To prove: Quad. ABCD is a parallelogram.
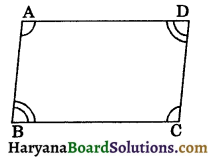
Proof: We have
∠A = ∠C…(1)
and ∠B = ∠D…(ii)
Adding (i) and (ii), we have
∠A + ∠B = ∠C + ∠D…(iii)
In a quadrilateral ABCD, we have
∠A + ∠B + ∠C + ∠D = 360°,
[∵ Sum of angles of a quadrilateral is 360°]
⇒ ∠A + ∠B + ∠A + ∠B = 360°, [Using (iii)]
⇒ 2(∠A + ∠B) = 360°
⇒ ∠A + ∠B = \(\frac{360^{\circ}}{2}\) = 180°…(iv)
Now, line segments BC and AD cut by AB,
such that
∠A + ∠B = 180°
⇒ BC || AD
Again, ∠A + ∠B = 180°.
⇒ ∠C + ∠B = 180° [From (i) ∠A = ∠C]
Now, line segments AB and CD cut by BC,
∠B + ∠C = 180°
⇒ AB || CD
Thus, AB || CD and BC || AD.
Hence, ABCD is a parallelogram. Proved
Theorem 8.6:
The diagonals of a parallelogram bisect each other.
Given: A parallelogram ABCD such that its diagonals AC and BD intersect at O.
To prove: OA = OC and OB = OD.
Proof: Since ABCD is a parallelogram.
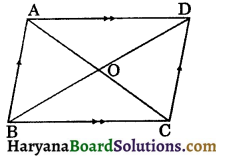
Therefore AB || CD and BC || AD.
Now, AB || CD and AC intersects.
∠BAC = ∠DCA, (Alternate interior angles)
∠BAO = ∠DCO …(1)
Again, AB || CD and BD intersects them.
∠ABD = ∠CDB, (Alternate interior angles)
⇒ ∠ABO = ∠CDO…(ii)
Now, in ΔAOB and ΔCOD, we have
∠BAO = ∠DCO, [From (i)]
AB = CD, (Opposite sides of parallelogram)
and ∠ABO = ∠CDO, [From (ii)]
∴ ΔAOB ≅ ΔCOD, (By ASA congruence rule)
⇒ OA = OC and OB = OD. Hence proved
![]()
Theorem 8.7:
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Given: ABCD is a quadrilateral in which the diagonals AC and BD bisect each other at O i.e., AO = OC and BO = OD.
To prove : Quadrilateral ABCD is a parallelogram.
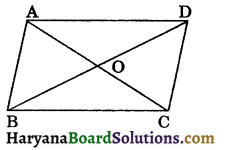
Proof: In ΔAOB and ΔCOD, we have
AO = OC, (Given)
∠AOB = ∠COD, (vertically opposite angles)
and BO = OD, (Given)
∴ ΔAOB ≅ ΔCOD, (by SAS congruence rule)
⇒ ∠BAO = ∠DCO, (CPCT)
⇒ ∠BAC = ∠DCA
But these are alternate interior angles.
∴ AB || CD
and similarly, AD || BC
Hence, quad. ABCD is a parallelogram. Hence Proved
5. Another Conditions for a Quadrilateral to be a parallelogram:
In this chapter, we have studied many properties and verified that if in a quadrilateral any one of those properties is satisfied, then it will be a parallelogram. Now, we study a required condition for a quadrilateral to be a parallelogram. It is stated in the form of a theorem as given below.
Theorem 8.8:
A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.
Given: A quadrilateral ABCD in which AB = CD and AB || CD
To prove: Quadrilateral ABCD is a parallelogram.
Construction : Join AC.

Proof: We have
AB || CD and AC intersects them.
⇒ ∠BAC = ∠DCA …(i)
(Alternate interior angles)
In ΔABC and ∠CDA, we have
AB = CD, (Given)
∠BAC = ∠DCA, [From (i)]
and AC = AC, (Common)
∴ ΔABC ≅ ΔCDA (By SAS congruence rule)
⇒ ∠BCA = ∠DAC, (CPCT)
But these are alternate interios angles.
∴ AD || BC
and AB || CD, (Given)
Hence, quad. ABCD is a parallelogram.
Hence Proved
The Mid Point Theorem: In this section we shall discuss some more properties of a triangle using properties of a parallelogram which is related to the mid points of sides of a triangle.
Theorem 8.9:
The line segment joining the mid points of two sides of a triangle is parallel to the third side and equal to half of it.
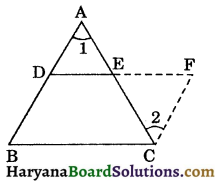
Given: D and E are the mid points of the sides AB and AC of the triangle ABC.
To prove : (i) DE || BC, (ii) DE = \(\frac{1}{2}\)BC.
Construction: Produce DE to F, such that EF = DE and join CF.
Proof: In ΔAED and ΔCEF, we have
AE = CE, (∵ E is the mid point of AC)
∠AED = ∠CEF, (Vertically opposite angles)
and DE = EF, (By construction)
∴ ΔAED ≅ ΔCEF, (By SAS congruence rule)
⇒ ∠1 = ∠2, (CPCT)
But these are alternate interior angles.
AB || FC ⇒ BD || FC …(i)
and AD = FC (CPCT)
But AD = BD
(∵ D is the mid point of AB)
∴ BD = FC ……(ii)
From (i) and (ii), we get
BD || FC and BD = FC
∴ BCFD is a parallelogram. [By theorem 8.8]
⇒ DF || BC,
(∵ Opposite sides of a parallelogram)
⇒ DE || BC
and DF = BC,
(∵ Oppsite sides of a parallelogram)
⇒ 2DE = BC,
[∵ DE = EF ⇒ DF = DE + EF = 2DE]
⇒ DE = \(\frac{1}{2}\)BC
Hence, DE || BC and DE = BC. Proved
![]()
Theorem 8.10:
The line drawn through the mid point of one side of a triangle, parallel to another side bisects the third side.
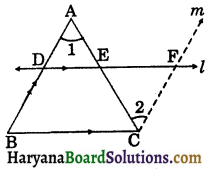
Given: A ΔABC, D is the mid point of AB and line through D parallel to BC intersects AC in E.
To prove: E is the mid point of AC.
Construction: Draw CM || BA intersects line l in F.
Proof: Since, AB || CM (By construction)
∴ BD || CF
and DF || BC (Given)
∴ BDFC is a parallelogram.
⇒ BD = CF,
(Opposite sides of a parallelogram)
But, BD = AD,
(∵ D is the mid point of AB)
∴ AD = CF …..(i)
Now, AB || CM and AC intersects them.
∠1 = ∠2,
(Alternate interior angles) …(ii)
In ΔADE and ΔCFE, we have
∠1 = ∠2 [From (i)]
∠AED = ∠CEF
(Vertically opposite angles)
and AD = CF [From (i)]
∴ ΔADE ≅ ΔCFE
(By AAS congruence rule)
⇒ AE = EC
Hence, E is the mid point of AC. Proved