HBSE 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.1

Haryana State Board HBSE 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.1

प्रश्न 1.
निम्नलिखित स्थितियों में चरों, अचरों और अंक गणितीय संक्रियाओं का प्रयोग करते हुए बीजीय व्यंजक प्राप्त कीजिए :
(i) संख्या y में से z को घटाना।
(ii) संख्याओं x और y के योग का आधा।
(ii) संख्या z को स्वयं उससे गुणा किया जाता है।
(iv) संख्याओं p और q के गुणनफल का एक चौथाई।
(v) दोनों संख्याओं x और y के वर्गों को जोड़ा जाता है।
(vi) संख्याओं m और n के गुणनफल के तीन गुने में संख्या 5 जोड़ना।
(vii) 10 में से संख्याओं y और z गुणनफल को घटाना।
(viii) संख्याओं a और b के गुणनफल में से उसके योग को घटाना।
हल :
दी गई स्थितियों के बीजीय व्यंजक निम्न होंगे-
(i) y – z
(ii) \(\frac{1}{2}\) (x + y)
(iii) z × z अथवा z²
(iv) \(\frac{1}{4}\)pq
(v) x² + y²
(vi) 3mn + 5
(vii) 10 – yz
(viii) ab – (a + b)

प्रश्न 2.
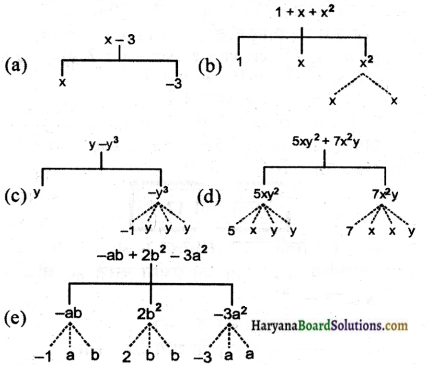
(i) निम्नलिखित व्यंजकों में पदों और उनके गुणनखण्डों को छाँटिए। पदों और उनके गुणनखण्डों को पेड़ आरेखों द्वारा भी दर्शाइए।
(a) x – 3
(b) 1 + x + x²
(c) y – y³
(d) 5xy² + 7x²y
(e) – ab + 2b² – 3a²
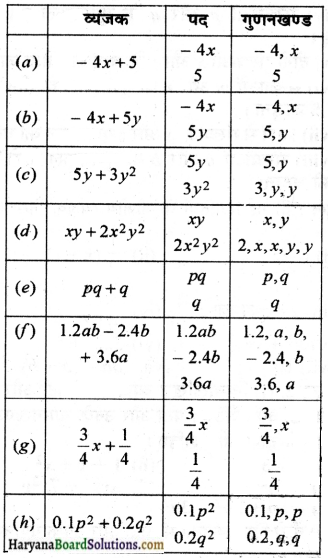
(ii) नीचे दिए व्यंजकों में, पदों और उनके गुणनखण्डों को छाँटिए।
(a) – 4x + 5
(b) – 4x + 5y
(c) 5y + 3y2
(d) xy + 2x2y2
(e) pq + q
(f) 1.2ab – 2.4b + 3.6a
(g) \(\frac{3}{4}\)x + \(\frac{1}{4}\)
(h) 0.1p² + 0.2q²
हल :
(i) व्यंजक में पद और उनके गुणनखण्ड पेड़ आरेख द्वारा निम्न प्रकार दर्शाया गया है-

(ii)

प्रश्न 3.
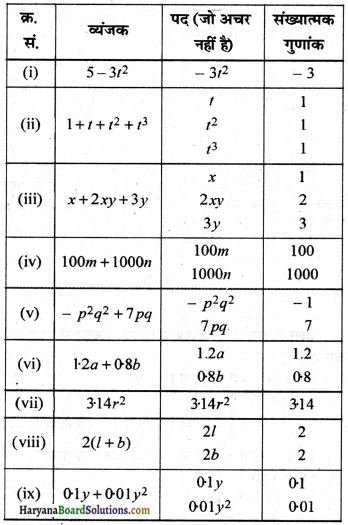
निम्नलिखित व्यंजकों में पदों के संख्यात्मक गुणांकों जो अचर न हों, की पहचान कीजिए।
(i) 5 – 3t²
(ii) 1 + t + t² + t³
(iii) x + 2xy + 3y
(iv) 100m + 1000n
(v) -p²q² + 7pq
(vi) 1.2a + 0.8b
(vii) 3.14r²
(viii) 2(l + b)
(ix) 0.1y + 0.01y²
हल :

प्रश्न 4.
(a) वे पद पहचानिए जिनमें x है और फिर इनमें x का गुणांक लिखिए :
(i) y²x + y
(ii) 13y² – 8yx
(iii) x + y + z
(iv) 5 + z + zx
(v) 1 + x + xy
(vi) 12xy² + 25
(vii) 7 + xy²
(b) वे पद पहचानिए जिनमें 2 है और फिर इनमें 2 का गुणांक लिखिए :
(i) 8 – xy²
(ii) 5y² + 7x
(ii) 2x²y – 15xy² + 7y²
हल :
(a)

	व्यंजक	x वाले पद	x के गुणांक
(i)	y2x + y	y2x	y2
(ii)	13y2 – 8yx	– 8yx	-8y
(iii)	x + y + 2	x	1
(iv)	5 + z + zx	zx	Z
(v)	1 + x + xy	X Xy	1 y
(vi)	12xy2 + 25	12xy2	12y2
(vii)	7 + xy2	xy2	y2

(b)

	व्यंजक	y2 वाले पद	y2 के गुणांक
(i)	8 – xy2	-xy2	-x
(ii)	5y2 + 7x	5y2	5
(iii)	2x2y – 15xy2 + 7y2	-15xy2 7y2	– 15x 7

प्रश्न 5.
निम्नलिखित व्यंजकों को एकपदी, द्विपद और त्रिपद के रूप में वर्गीकृत कीजिए :
(i) 4y – 7z
(ii) y²
(iii) x + y – xy
(iv) 100
(v) ab – a – b
(vi) 5 – 3t
(vii) 4p²q – 4pq²
(viii) 7mn
(ix) z² – 3z + 8
(x) a² + b²
(xi) z² + z
(xii) 1 + x + x²
हल :
केवल एक पद वाले बीजीय व्यंजक एकपदी कहलाते हैं। अतः एकपदी व्यंजक (ii), (iv) और (viii) हैं।
दो पद वाले बीजीय व्यंजक द्विपद व्यंजक कहलाते हैं।
अतः द्विपद व्यंजक : (i), (vi), (vii), (x) और (xi) हैं।
जिन बीजीय व्यंजकों में तीन पद होते हैं, उन्हें त्रिपद व्यंजक कहते हैं।
अतः त्रिपद व्यंजक : (iii), (v), (ix) और (xii) हैं।

प्रश्न 6.
बताइए कि दिए हुए पदों के युग्म समान पदों के हैं या असमान पदों के हैं :
(i) 1, 100
(ii) – 7x, \(\frac{5}{2}\)x
(iii) – 29x, – 29y
(iv) 14xy, 42yx
(v) 4m²p, 4mp²
(vi) 12xz, 12x²z²
हल :
(i) समान
(ii) समान
(iii) असमान
(iv) समान
(v) असमान
(vi) असमान।

प्रश्न 7.
निम्नलिखित में समान पदों को छाँटिए :
(a) -xy², -4yx², 8x², 2xy², 7y, – 11x²,- 100x, – 11yx, 20x²y, -6x², y, 2xy, 3x
(b) 10pq, 7p, 8q, -p²q², -7qp, – 100g, -23, 12q²p², -5p², 41, 2405p, 78qp, 13p²q, qp², 701p²
हल :
(a) दिए गए पर्दो में समान पदों के समूह निम्न होंगे-
-xy², 2xy²; -4yx², 20x²y; 8x², -11x², -6x²; 7y, y; -100x, 3x और -11yx, 2xy
(b) दिए गए पदों में समान पदों के समूह निम्न होंगे-
10pq, – 7gp, 78qp; 7p, 2405p 8q, – 100q; – p²q², 12q²p²; – 23, 41; – 5p², 701p² और 13p²q, qp²